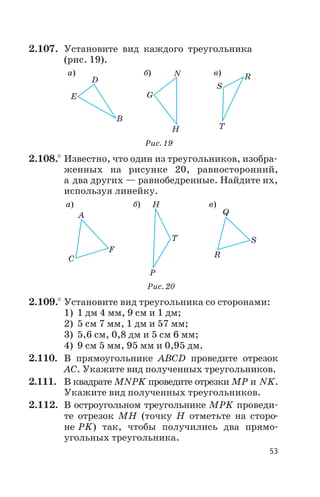
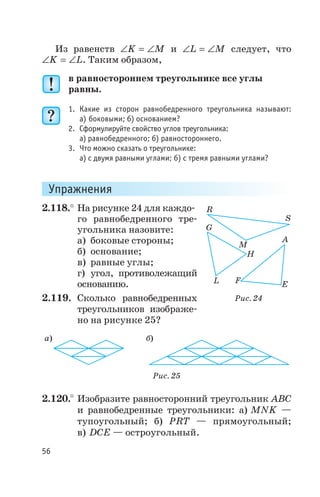
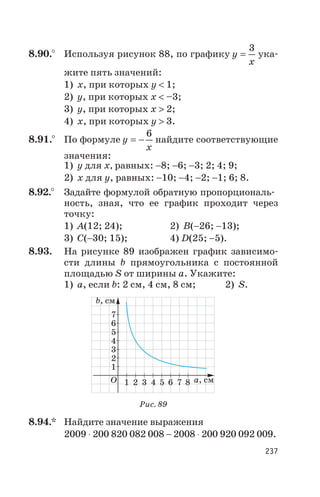
Документ представляет собой учебное пособие по математике для учащихся 6 класса, описывающее основные понятия десятичных дробей и рациональных чисел. В пособии представлены упражнения, направленные на освоение материала, включая преобразование обыкновенных дробей в десятичные и различные математические задачи. Дополнительно указаны способы записи и чтения десятичных дробей, а также исторические сведения о введении десятичной системы.


![Ìàòåìàòèêà : ó÷åá. ïîñîáèå äëÿ 6 êë. îáùåîáðàçî-
âàò. ó÷ðåæäåíèé ñ ðóñ. ÿç. îáó÷åíèÿ / Å. Ï. Êóçíåöî-
âà [è äð.] ; ïîä ðåä. Ë. Á. Øíåïåðìàíà. — Ìèíñê :
Íàö. èí-ò îáðàçîâàíèÿ, 2010. — 320 ñ. : èë.
ISBN 978−985-465-629-8.
ÓÄÊ 51(075.3=161.3=161.1)
ÁÁÊ 22.1ÿ721
ISBN 978-985-465-629-8 © Îôîðìëåíèå. ÍÌÓ «Íàöèîíàëüíûé
èíñòèòóò îáðàçîâàíèÿ», 2010
ÓÄÊ 51(075.3=161.3=161.1)
ÁÁÊ 22.1ÿ721
Ì34
Ì34
Ð å ö å í ç å í ò û:
êàôåäðà ãåîìåòðèè, òîïîëîãèè è ìåòîäèêè ïðåïîäàâàíèÿ
ìàòåìàòèêè Áåëîðóññêîãî ãîñóäàðñòâåííîãî óíèâåðñèòåòà
(êàíäèäàò ôèç.-ìàò. íàóê, äîöåíò Ñ. Ã. Êîíîíîâ);
ìåòîäèñò âûñøåé êàòåãîðèè óïðàâëåíèÿ ó÷åáíî-ìåòîäè÷åñêîé
ðàáîòû Àêàäåìèè ïîñëåäèïëîìíîãî îáðàçîâàíèÿ Ì. Â. Êðûëîâè÷;
ó÷èòåëü ìàòåìàòèêè âûñøåé êàòåãîðèè ãèìíàçèè ¹ 1
ã. Áàðàíîâè÷è À. Å. Ñàíþê
À â ò î ð û:
Å. Ï. Êóçíåöîâà, Ã. Ë. Ìóðàâüåâà, Ë. Á. Øíåïåðìàí,
Á. Þ. ßùèí, Þ. Ê. Âîéòîâà](https://image.slidesharecdn.com/6mk-160829114936/85/6-m-k-3-320.jpg)