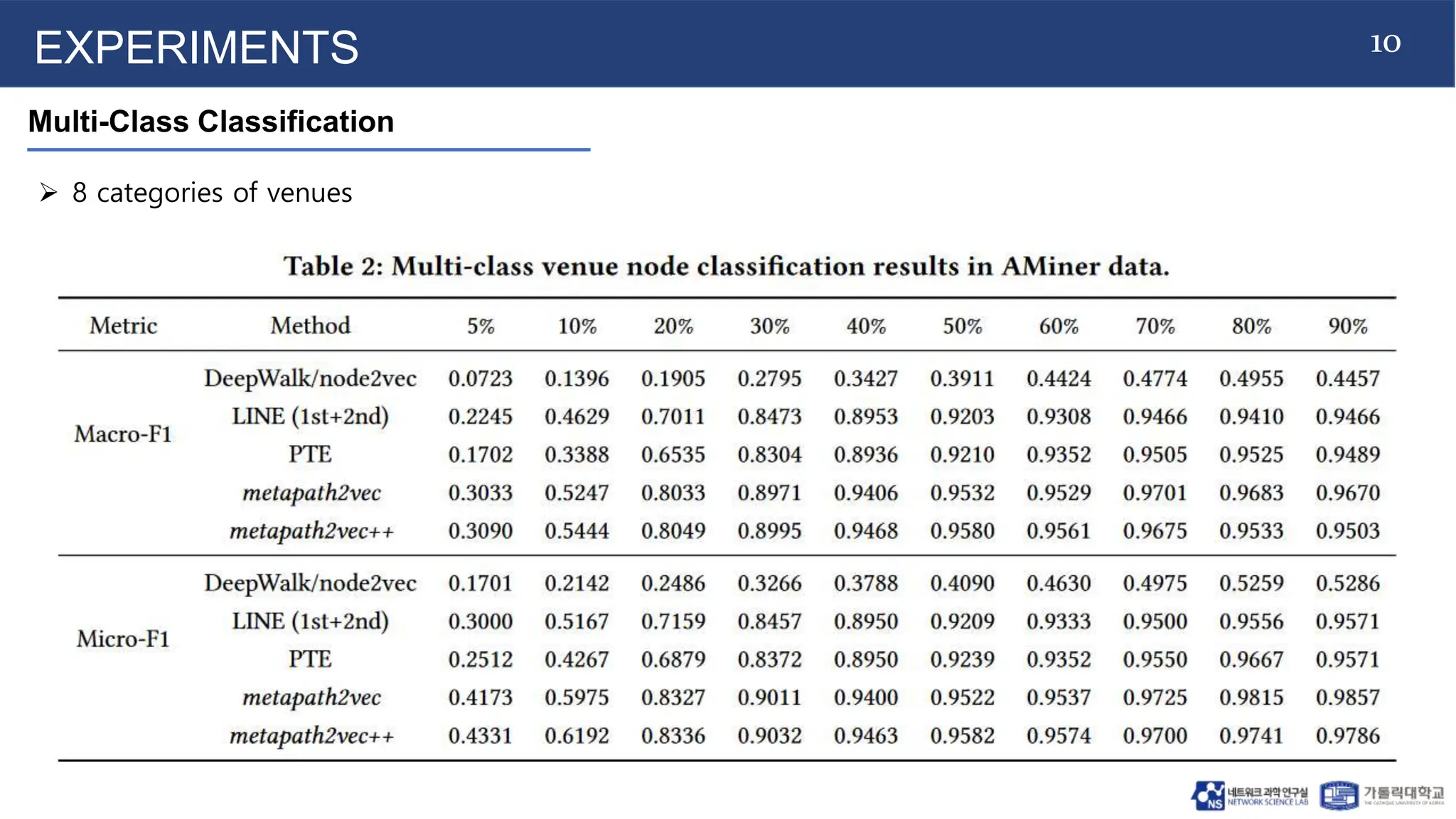
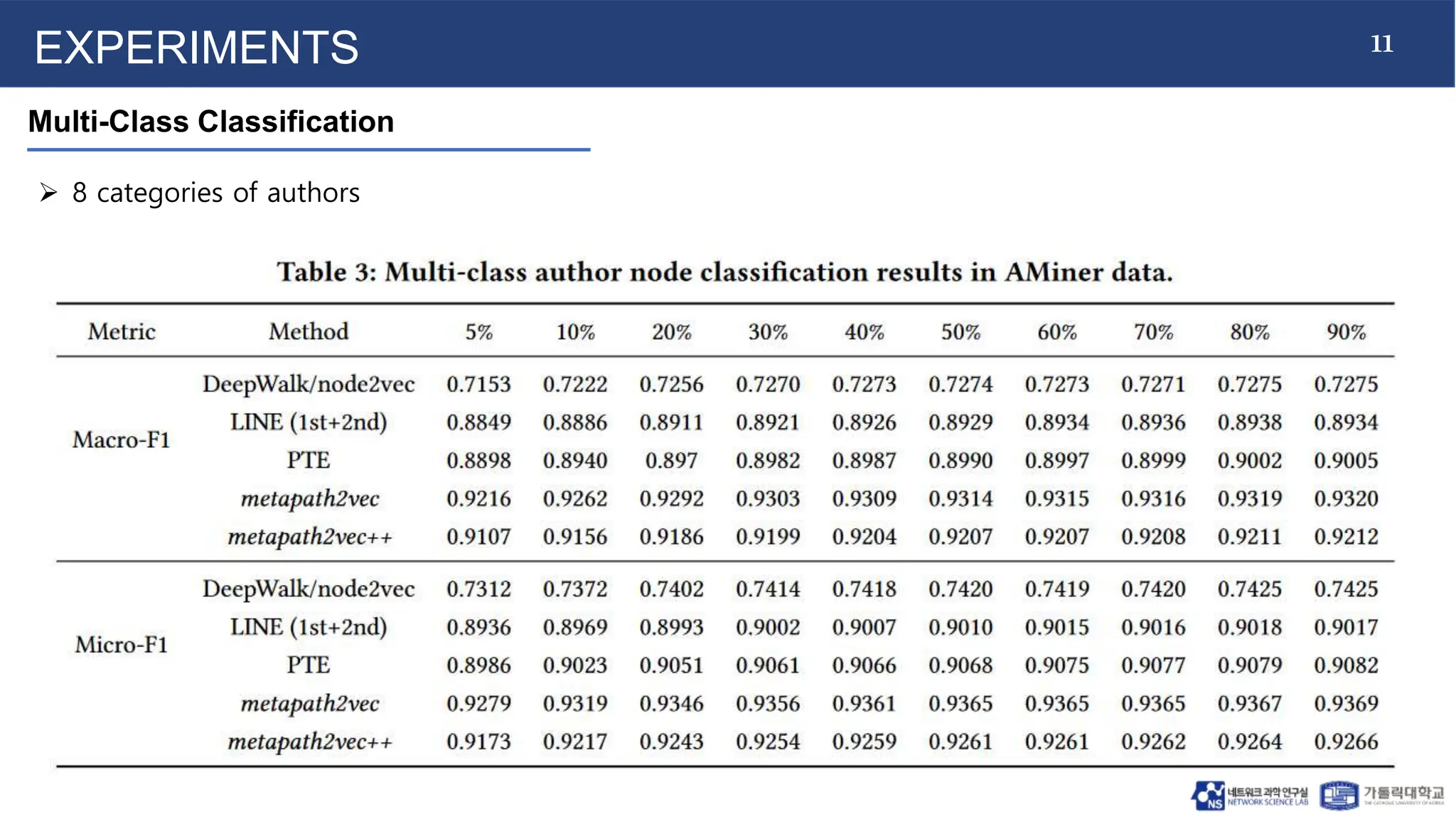
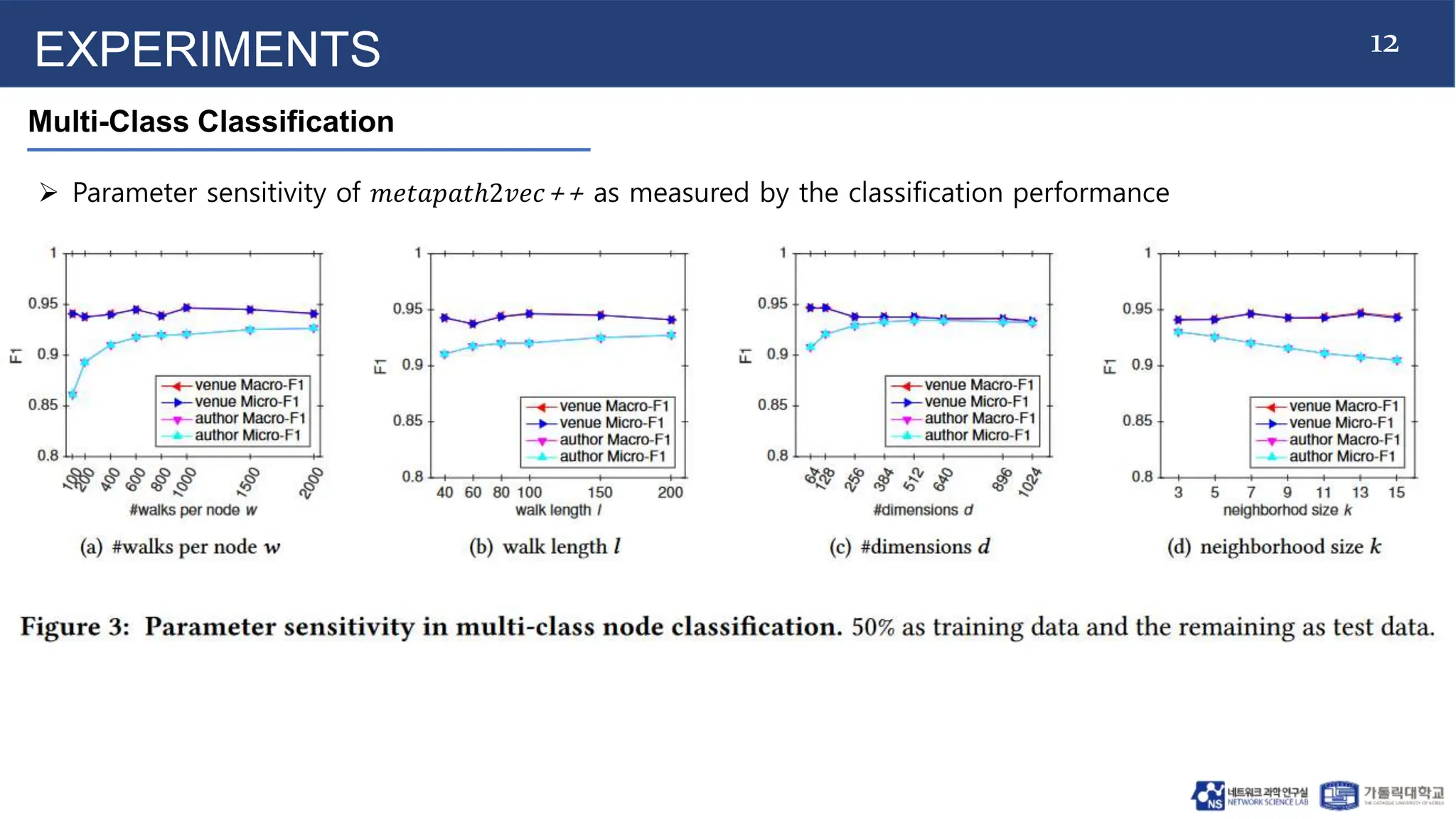
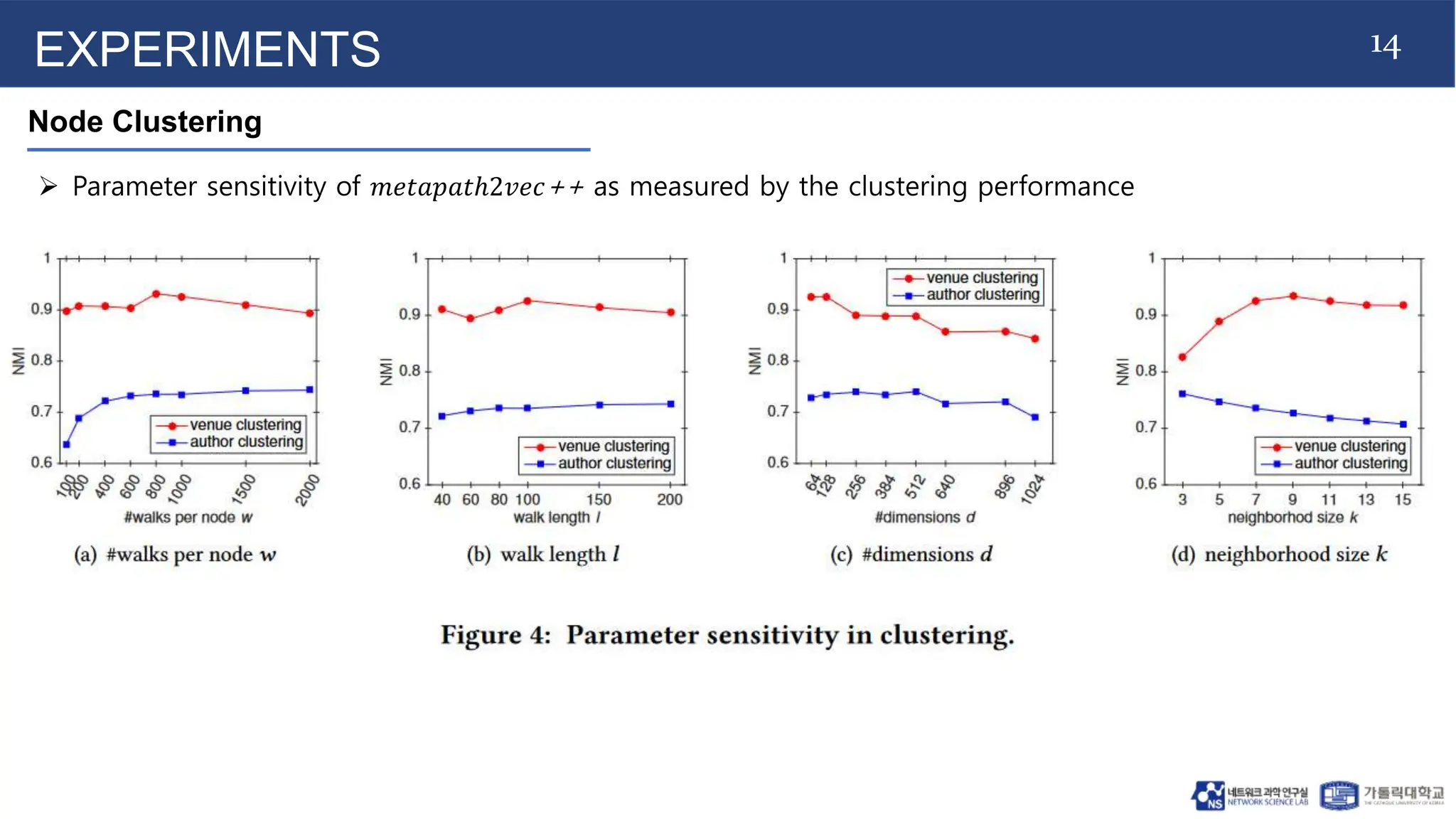
The document introduces metapath2vec and its extension metapath2vec++ for heterogeneous network representation learning, addressing challenges posed by the diversity of node types and relationships in such networks. It details the frameworks' capabilities to preserve structural and semantic correlations while demonstrating their effectiveness through extensive experiments in tasks like node classification and clustering. The study emphasizes the development of unique techniques, including meta-path-guided random walks and heterogeneous negative sampling, to optimize learning and improve various network mining applications.

1. Jin-Woo Jeong
Network Science Lab
Dept. of Mathematics
The Catholic University of Korea
E-mail: zeus0208b@catholic.ac.kr
Yuxiao Dong, Nitesh V. Chawla, Ananthram Swami
KDD ’17

2. 1
 INTRODUCTION
• Motivation
• Introduction
 PROBLEM DEFINITION
 METAPATH2VEC FRAMEWORK
• metapath2vec
• Metapath2vec++
EXPERIMENTS
• Data
• Experimental Setup
• Multi-Class Classification
• Node Clustering
• Case Study: Similarity Search
• Case Study: Visualization
 CONCLUSION
Q/A

3. 2
INTRODUCTION
Motivation
 A number of recent research publications have proposed word2vec-based network representation learning
frameworks, such as DeepWalk, LINE , and node2vec.
 these work has thus far focused on representation learning for homogeneous networks—representative of
singular type of nodes and relationships.
 Yet a large number of social and information networks are heterogeneous in nature, involving diversity of
node types and/or relationships between nodes
 These heterogeneous networks present unique challenges that cannot be handled by representation
learning models that are specifically designed for homogeneous networks.
 By solving these challenges, the latent heterogeneous network embeddings can be further applied to
various network mining tasks, such as node classification, clustering, and similarity search.

4. 3
INTRODUCTION
Introduction
 We present the 𝑚𝑒𝑡𝑎𝑝𝑎𝑡ℎ2𝑣𝑒𝑐 and its extension 𝑚𝑒𝑡𝑎𝑝𝑎𝑡ℎ2𝑣𝑒𝑐++ frameworks.
 Contributions
• Formalizes the problem of heterogeneous network representation learning and identifies its unique
challenges resulting from network heterogeneity.
• Develops effective and efficient network embedding frameworks, 𝑚𝑒𝑡𝑎𝑝𝑎𝑡ℎ2𝑣𝑒𝑐 & 𝑚𝑒𝑡𝑎𝑝𝑎𝑡ℎ2𝑣𝑒𝑐++,
for preserving both structural and semantic correlations of heterogeneous networks.
• Through extensive experiments, demonstrates the efficacy and scalability of the presented methods in
various heterogeneous network mining tasks, such as node classification and node clustering.
• Demonstrates the automatic discovery of internal semantic relationships between different types of
nodes in heterogeneous networks by metapath2vec & metapath2vec++, not discoverable by existing
work.

5. 4
PROBLEM DEFINITION
Problem Definition

6. 5
METAPATH2VEC FRAMEWORK
metapath2vec
 Homogeneous Network Embedding
• 𝐺𝑖𝑣𝑒𝑛 𝐺 = 𝑉, 𝐸
• where 𝑁(𝑣) is the neighborhood of node v in the network G
 Heterogeneous Network Embedding: metapath2vec
• Heterogeneous Skip-Gram
• 𝐺𝑖𝑣𝑒𝑛 𝐺 = 𝑉, 𝐸, 𝑇
• where 𝑁𝑡(𝑣) denotes 𝑣′
𝑠 neighborhood with the 𝑡𝑡ℎ
type of nodes
• 𝑝 𝑐𝑡|𝑣; 𝜃 =
𝑒𝑋𝑐𝑡∙𝑒𝑋𝑣
𝑢∈𝑉 𝑒𝑋𝑢∙𝑒𝑋𝑣
, where 𝑋𝑣 is the 𝑣𝑡ℎ
row of 𝑋, representing the embedding vector for node 𝑣.
 Negative Sampling
log 𝜎 𝑋𝑐𝑡
∙ 𝑋𝑣 +
𝑚=1
𝑀
𝔼𝑢𝑚~ 𝑃(𝑢)[log 𝜎 −𝑋𝑢𝑚 ∙ 𝑋𝑣 ]

7. 6
METAPATH2VEC FRAMEWORK
metapath2vec
 Meta − Path Based Random Walks
• Given a heterogeneous network 𝐺 = 𝑉, 𝐸, 𝑇 and a meta − path scheme 𝒫: 𝑉1
𝑅1
𝑉2
𝑅2
⋯ 𝑉𝑡
𝑅𝑡
𝑉𝑡+1 ⋯
𝑅𝑙−1
𝑉𝑙
• wherein 𝑅 = 𝑅1 ∘ 𝑅2 ∘ · · · ∘ 𝑅𝑙−1 defines the composite relations between node types 𝑉1 and 𝑉𝑙
• the transition probability at step 𝑖 is defined as follows:
• where 𝑣𝑖
𝑡
∈ 𝑉𝑡 and 𝑁𝑡+1(𝑣𝑖
𝑡
) denote the 𝑉𝑡+1 type of neighborhood of node 𝑣𝑖
𝑡
.

8. 7
METAPATH2VEC FRAMEWORK
metapath2vec++
 Heterogeneous negative sampling
• 𝑝(𝑐𝑡|𝑣; 𝜃) is adjusted to the specific node type 𝑡, that is,

9. 8
EXPERIMENTS
Data
 Two heterogeneous network
• AMiner Computer Science (CS) dataset
• AMiner CS dataset consists of 9,323,739 computer scientists and 3,194,405 papers from 3,883
computer science venues—both conferences and journals—held until 2016
• They construct a heterogeneous collaboration network, in which there are three types of nodes:
authors, papers, and venues.
• Database and Information Systems (DBIS) dataset
• It covers 464 venues, their top-5000 authors, and corresponding 72,902 publications.
• They also construct the heterogeneous collaboration networks from DBIS wherein a link may
connect two authors, one author and one paper, as well as one paper and one venue.

10. 9
EXPERIMENTS
Experimental Setup
 Compare 𝑚𝑒𝑡𝑎𝑝𝑎𝑡ℎ2𝑣𝑒𝑐 and 𝑚𝑒𝑡𝑎𝑝𝑎𝑡ℎ2𝑣𝑒𝑐++ with several recent network representation learning methods:
• DeepWalk / node2vec: With the same random walk path input (𝑝 = 1 & 𝑞 = 1 in node2vec), we find that
the choice between hierarchical softmax (DeepWalk) and negative sampling (node2vec) techniques does
not yield significant differences. Therefore we use p=1 and q=1 in node2vec for comparison.
• LINE: We use the advanced version of LINE by considering both the 1st- and 2nd-order of node proximity;
• PTE: We construct three bipartite heterogeneous networks (author–author, author–venue, venue–venue)
and restrain it as an unsupervised embedding method;
• Spectral Clustering / Graph Factorization: With the same treatment to these methods in node2vec, we
exclude them from our comparison, as previous studies have demonstrated that they are outperformed
by DeepWalk and LINE.
(1) The number of walks per node w: 1000;
(2) The walk length l: 100;
(3) The vector dimension d: 128 (LINE: 128 for each order);
(4) The neighborhood size k: 7;
(5) The size of negative samples: 5.

11. 10
EXPERIMENTS
Multi-Class Classification
 8 categories of venues

12. 11
EXPERIMENTS
Multi-Class Classification
 8 categories of authors

13. 12
Multi-Class Classification
EXPERIMENTS
 Parameter sensitivity of 𝑚𝑒𝑡𝑎𝑝𝑎𝑡ℎ2𝑣𝑒𝑐++ as measured by the classification performance

14. 13
Node Clustering
EXPERIMENTS
 Node Clustering with k-means algorithm

15. 14
Node Clustering
EXPERIMENTS
 Parameter sensitivity of 𝑚𝑒𝑡𝑎𝑝𝑎𝑡ℎ2𝑣𝑒𝑐++ as measured by the clustering performance

16. 15
Case Study: Similarity Search
EXPERIMENTS
 Similarity search of 𝑚𝑒𝑡𝑎𝑝𝑎𝑡ℎ2𝑣𝑒𝑐++

17. 16
Case Study: Visualization
EXPERIMENTS

18. 17
Conclusion
Conclusion
 We formally define the representation learning problem in heterogeneous networks in which there exist
diverse types of nodes and links.
 We develop the meta-path-guided random walk strategy in a heterogeneous network, which is capable of
capturing both the structural and semantic correlations of differently typed nodes and relations.
 We formalize the heterogeneous neighborhood function of a node, enabling the skip-gram-based
maximization of the network probability in the context of multiple types of nodes.
 We achieve effective and efficient optimization by presenting a heterogeneous negative sampling
technique. Extensive experiments demonstrate that the latent feature representations learned by
𝑚𝑒𝑡𝑎𝑝𝑎𝑡ℎ2𝑣𝑒𝑐 and 𝑚𝑒𝑡𝑎𝑝𝑎𝑡ℎ2𝑣𝑒𝑐++ are able to improve various heterogeneous network mining tasks,
such as similarity search, node classification, and clustering.

19. 18
Q & A
Q / A