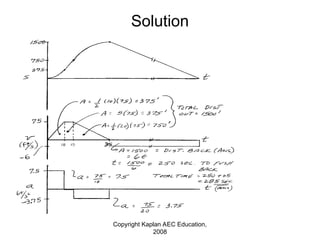
The document is a review of dynamics for the FE exam, covering topics such as kinematics, kinetics, forces, energy, and work related to particle motion and rigid bodies. It includes principles like Newton's laws, the use of free body diagrams, and conservation of momentum and energy, along with sample problems for practical application. The document also addresses different types of motion including rectilinear, curvilinear, and constraints in mechanical systems.

1. FE Exam: Dynamics review
D. A. Lyn
School of Civil Engineering
21 February 2012

2. Preliminaries
• Units (relevant quantities: g, displacement,
velocity, acceleration, energy, momentum, etc.)
• Notation (dot, vector)
• Vectors (components and directions/signs,
addition (graphical), dot and cross products,
vector polygons)
• Coordinate systems (Cartesian and curvilinear,
fixed and moving or relative, unit vectors)
• Statics (free body diagram)

3. Classification of dynamics and problems
• Kinematics: description of motion without reference to forces
– Particle (no rotation about itself) and rigid-body
– Coordinate systems (Cartesian, curvilinear, rotation)
– Constraints on motion
• Kinetics: inclusion of forces (mass, or momentum or energy)
– Types of forces: conservative (gravitational, spring, elastic
collisions) and non-conservative (friction, inelastic collisions)
– Newton’s 2nd
law: linear and angular momentum
• Use of free body diagram to deal with external forces
– Particles and rigid body (system of particles)
– Impulse (time involved) and momentum
• still working with vectors
– Work (distances involved) and energy (velocities involved)
• working with scalars (usually easier)

4. Particle kinematics
• General relations between displacement
(r), velocity (u), and acceleration (a)
• Given a formula for (or graph of) r as
function of t, take derivatives to find u and
a
– Given a formula for u or a as function of t,
integrate to find r or u
Special case: constant acceleration,
( ) , ( ) = ( , , ), ( , , ), ( , , )
d d
t t x y z x y z x y z
dt dt
      
r u
u r a u r r u a
 
    
 
0

a a
2
0 0
1
( ) ( 0) , ( ) ( 0) ( 0)
2
t t t t t t t t


          
 
u u a r r u a

5. Sample problems
• The position of a particle moving horizontally is described by
, with s in m and t in s. At t = 2 s, what
is its acceleration?
Soln: Take derivatives of s with respect to t, and evaluate at
t=2s ( ) so a(t=2s) = 4
m/s2
.
• Projectile problem: A projectile is launched with an initial speed
of v0=100 ft/s at =30° to the horizontal, what is the horizontal
distance, L, covered by the projectile when it lands again?
Soln: constant acceleration (only gravitational
acceleration involved) problem, so apply
formulae in two directions
2
( ) 2 8 3
s t t t
  
( ) ( ) 4 8, ( ) ( ) 4
u t s t t a t s t
     
 
 
 
2
0 0
2
0 0
/ 2
/ 2
end x end x end
end y end y end
x x v t a t
y y v t a t
  
  
0 0
0, , 100cos30 , 100sin30
x y x y
a a g v v
     
wish to find L=xend-x0, for yend-y0=0, so we solve
L=v0xt end and 0=v0ytend-g(tend
2
/2) for tend and L;
tend=3.1 s and L=269.2 ft
L
v0

x
y

6. Kinetics of a particle
• Linear momentum, L=mu (appearance of mass, i.e., inertia)
• Newton’s 2nd
law:
• Forces determined from free body diagram (as in statics)
– Types of forces: gravitational, frictional, external
• Angular momentum (about a point O) ,
• Newton’s 2nd
law:
• Impulse (used in impact and collision problems),
– momentum conservation:
– mini-problem: A golf ball of mass 50-g is hit with a club. If the initial
velocity of the ball is 20 m/s, what is the impulse imparted to the ball? If
the contact duration was 0.05 s, what was the average force on the ball?
m
 
F a L

0 m
 
H r u
0 0

M H

2
1
1 2
t
t
dt
 
Imp F
2
1
2 1 1 2
t
t
dt

  
L L Imp F
1 2 1 2 2
1 2
0
0 Imp (0.05 kg)(20 m/s) = 1 Ns
Imp 1 Ns 1 Ns / 0.05 s 20 N
t
avg avg
L L mv
F dt F t F



    
      


7. Problem: kinetics of a particle (truck)
• A truck of weight W = 4000 lbf moves down a
=10° incline at an initial speed of u0 = 20 ft/s.
A constant braking force of Fbrk=1200 lbf is
experienced by the truck from a time, t = 0.
What is the distance covered by the truck
before it stops from the time that the braking
force is applied?
• kinematics problem:
2
sin , sin 4.1 ft/s
brk
brk net s s
F
F W F ma W mg a g
W
 


         
 
 
0
2 2
0 0
( ) ( 0) / 4.9 s
( ) ( 0) ( / 2) / 2 48.8 ft
end s end end s
end end s end s
u t t u t a t t u a
s t t s t u t a t u a
      
      
Notes: forces involved – kinetics problem, rectilinear (straight-line) motion:
determine net force on truck in direction of motion, apply Newton’s 2nd
law to
evaluate distance covered
From free body diagram, sum of forces in direction of motion,
u0

W
Fbrk
W sin
mas
s

8. Curvilinear coordinates and motion
• Plane motion (motion on a surface, i.e., in only two
dimensions)
– Tangential (t) and normal (n) coordinates
where  is the radius of curvature of
particle path
– Radial (r) and transverse () or polar coordinates
– Special case: pure circular motion at an angular frequency,
t
2
( ) , ( ) ( ) ( 2 )
r r
t r r t r r r r
 
   
     
v e e a e e
   
  
2
( ) , ( )
t n t
v
t v t v



  


 
v e a e e

2
2 2
, 0, , ,
0, ,
t r n
r v r r
v
r r r v r r r
r

   
    
     
     
e e e e
 

  
 
x
x 1
y
y 1
r

er
en
et
e
particle
path
particle
at tim e t
r
v
=
r


a r
r= 
2
a
r
r

= 
.
( is the angular acceleration)

9. Particle kinetics problem
• Find the tension, T, in the string and the
angular acceleration, , if at the position
shown the a sphere of mass, m=10 kg,
has a tangential velocity of v0=4 m/s.
• Choose a polar coordinate system,
perform free body analysis to determine
sum of forces, and set equal to ma.
2
0
2
0 0 0
2
0 0
dir'n: - cos / cos 352 N
dir'n: sin sin / 8.2/s
r
v
r T W ma mv R T m g
R
W ma mR W mR

 
     


       


 
       
 
W
T
r

R
0
v0
m

10. Energy and work
• Work of a force,F, resulting in a change in position from state 1
to state 2:
– Constant force in rectilinear motion, Fxx2-x1)
– Gravitational force, -Wy2-y1), y>0 upwards
– Spring force, -k(x2
2
-x1
2
)/2, (x2<x1, returning to undeformed state)
• Kinetic energy,
• Relation between work and kinetic energy:
• for conservative forces (such as gravitational and spring forces,
but not frictional forces), a potential energy function, V, can be
defined such that
– Gravitational force: V = Wy, spring force, V=kx2
/2
• For conservative forces, an equation for conservation of energy
can be expressed as or
2
1 2
1
U d
  
F r
2
/ 2
T mv

1 2 2 1
U T T
  
1 2 1 2
U V V
  
1 2 2 1
V V T T
   1 1 2 2
T V T V
  

11. A problem solved using energy
principles
• A 2-kg block (A) rests on a frictionless
plane inclined at an angle =30°. It is
attached by an inextensible cable to a
3-kg block (B) and to a fixed support.
Assume pulleys are frictionless and
weightless. If initially both blocks are
stationary, how far will the 2-kg block
travel before its speed is 4 m/s?
• Motion constraints: sB=sA/2 (and yA=-2yBsin), and vB=vA/2
• Frictionless system  conservative gravitational forces only, only
distances and speeds explicitly involved apply energy equation
        
2
2 2 2
1 2
Initially, 0; at end, / 2 / 2 / 2 1 / /
A A B A B A
A B
T T mv mv m v m m v v
 
    
 
   
 
1 2 2 1 2 1 2
1 2
2
2
2
2
1
1 1 1
2 2sin
1 2.24 m 0 (
2 1 / 2 sin
A A B B A A B B A A B B
A A B B B B B
A A A A
A A A A A
A B B
A
B A A A
V V T T T W y W y W y W y W y W y U
m v m v W y W
W y W y
m v W y W
v m v
y
g W W m v



            
 

 
 

  
      
 

 

   

  
  
   
 
 


     
 
 
  
 
 
Block A rises)
/ sin 2 4.48 m
A A
s y y

     
3 kg
2 kg
=30
State 1
B
A
3 kg
3 kg
2 kg
2 kg
= 30 = 30
State 1 State 2
s y
B = B
yA
v
B
B
A
A sA

12. Constrained motion, reference frames,
relative motion
• Constrained-motion problems – choice of reference
frames: relative motion (in a plane)
• Choice of reference frames – motion relative to a point A
in a moving reference frame
– For plane motion, note direction of components, e.g., rB/A is
perpendicular to rB/A, etc.
– For points on the same rigid body,
/ / /
= , = , =
B A B A B A B A B A B A
  
r r r u u u a a a
       
/ / / / / / / /
, 2
B A B A B A B A B A B A B A B A
         
u Ω r r a Ω r Ω Ω×r r Ω r

  
   
/ /
0
B A B A
 
r r
 

13. Problem: Kinematics of rigid body example
• The end A of rod AB of length L = 0.6 m moves
at velocity VA = 2 m/s and acceleration, aA = 0.2
m/s2
, both to the left, at the instant shown, when
 = 60°. What is the velocity, VB ,and
acceleration, aB , of end B at the same instant?
Pure kinematics problem:
 
/
2
/ /
2
2
2
2
cos , sin cot 1.16 m/s
0 sin cos cos
sin cos sin sin
cos sin
B A B A B A
B A B A
B A B A B A B A
A A A
Bx A
By B
V V L
V L V L V V
a a L L
a a V
a a L L
L L L
a a L L

    
 

     
   
   
       
     
          


          
 
    
u u Ω r
a a Ω r Ω Ω×r

  
 
2
2
1 cos 11.7 m/s
sin
A
A
V
a
L


  
V , a
A , A
A
B
V ?
B
a ?
B

x
y
aA
aB
 

L
2
L
rB/A
VA
VB


L
rB/A

14. Kinetics of a system of particles (or rigid
body)
• For a system of particles (or a rigid body), analysis is performed
in terms of the mass center, G, located at radial vector, rG, and
total mass m
• Equations of motions:
where aG is the acceleration of the mass center, and HG is the
angular momentum about the mass center
− For a system with no external forces or moment acting, then linear
momentum, L, and angular momentum, H, is conserved, i.e., remains
constant
• For a system of particles (or a rigid body), and
where the mass moment of inertia I is defined by
(Standard formulae for I = mk2
, where k is the radius of
gyration, for standard bodies are listed in tables; be careful about
which axis I is defined, whether centroidal axis or not, remember
parallel axis theorem)
or
G i i G
m m m dm
 
 
r r r r
eff eff
= and
G G G
m
   
 
F a L F M H M
 
G G G
I I
 
H ω α
 
2 2
or
i i
I r m I r dm
 
 
G G
I

H ω

16. Problem: two-particle system
• A particle A of mass m and and a particle B, of
mass 2m are connected by rigid massless rod of
length R. If mass B is suddenly given a vertical
velocity v perpendicular to the connecting rod,
determine the location of the mass center, the
velocity of the mass center, the angular
momentum, and the angular velocity of the
system soon after the motion begins.
     
   
       
 
/ /
2 2
/ /
2
3 2
3
2 2
3 2
3 3
2 1 2
0 2
3 3 3
A B G A A B B G A B G A B A
G A B G A A B B G A B G B
G A G A A B G B B
G G G A A G B B G
m m m m m m
m m m m m m v
m m m R m R v mvR
I I m r m r 
         
         
 
 
      
   
 
 
    
r r r r r r r r r r
L u u u u u u u u j
H r u r u k k k
H ω ω k
2 2
2
0
2
0
2 1 2
2
3 3 3
2 2
3 3
m R m R mR
v
mv R mR
R
 
 
 
 
 
 
 
   
 
 
 
 
   
k k
k k
v
x
y j
rA
rB
r r
B A
-
A B
G
m 2m
(2 /3)
v j
A B
G
m 2m


17. Problem: rigid-body kinetics
• What is the angular acceleration, , of the
60-kg (cylindrical) pulley of radius R = 0.2 m
and the tension in the cable if a 30-kg block
is attached to the end of the cable?
• Analysis of block
− Kinematic constraint (ablock=R)
O
R
m=30-kg
m pulley=60-kg
 
( )
y y y
F ma T W ma m R
T m g R


     
  

• Analysis of pulley
 
2 2
0 0 0 pulley pulley
where / 2 / 2
M I I m R TR m R
 
   

  2
pulley pulley
2 1
Solve for and : 147 N, 24.5
1 2 / s
mg T
T T
m m m R
 
   

R
T T
W =mg

a R
y= 
y
+

18. Dynamics Outline and
Problem - Solutions
as Provided by Kaplan

19. Copyright Kaplan AEC Education,
2008
Dynamics Outline Overview
DYNAMICS, p. 205
KINEMATICS OF A PARTICLE, p. 206
• Relating Distance, Velocity and the Tangential
Component of Acceleration
• Constant Tangential Acceleration
• Rectilinear Motion
• Rectangular Cartesian Coordinates
• Circular Cylindrical Coordinates
• Circular Path

20. Copyright Kaplan AEC Education,
2008
Dynamics Outline Overview Continued
RIGID BODY KINEMATICS, p. 203
• The Constraint of Rigidity
• The Angular Velocity Vector
• Instantaneous Center of Zero Velocity
• Accelerations in Rigid Bodies

21. Copyright Kaplan AEC Education,
2008
Dynamics Outline Overview Continued
NEWTON’S LAWS OF MOTION, p. 210
• Applications to a Particle
• Systems of Particles
• Linear Momentum and Center of Mass
• Impulse and Momentum
• Moments of Force and Momentum

22. Copyright Kaplan AEC Education,
2008
Dynamics Outline Overview Continued
WORK AND KINETIC ENERGY, p. 219
• A Single Particle
• Work of a Constant Force
• Distance-Dependent Central Force

23. Copyright Kaplan AEC Education,
2008
Dynamics Outline Overview Continued
KINETICS OF RIGID BODIES, p. 225
• Moment Relationships for Planar Motion
• Work and Kinetic Energy

24. Copyright Kaplan AEC Education,
2008
Kinematics of Particles—1D Motion

25. Copyright Kaplan AEC Education,
2008
Solution

26. Copyright Kaplan AEC Education,
2008
Kinematics of Particles—1D Motion

27. Copyright Kaplan AEC Education,
2008
Solution

28. Copyright Kaplan AEC Education,
2008
Solution (continued)

29. Copyright Kaplan AEC Education,
2008
2D Motion—Rectangular Cartesian
Coordinates

30. Copyright Kaplan AEC Education,
2008
Solution

31. Copyright Kaplan AEC Education,
2008
2D Motion—Plane Polar Coordinates

32. Copyright Kaplan AEC Education,
2008
Solution

33. Copyright Kaplan AEC Education,
2008
Instantaneous Center of Zero Velocity

34. Copyright Kaplan AEC Education,
2008
Solution

35. Copyright Kaplan AEC Education,
2008
Evaluation of Accelerations

36. Copyright Kaplan AEC Education,
2008
Solution

37. Copyright Kaplan AEC Education,
2008
Solution (continued)

38. Copyright Kaplan AEC Education,
2008
Solution (continued)

39. Copyright Kaplan AEC Education,
2008
Newton’s 2nd
Law

40. Copyright Kaplan AEC Education,
2008
Solution

41. Copyright Kaplan AEC Education,
2008
Solution (continued)

42. Copyright Kaplan AEC Education,
2008
Solution (continued)

43. Copyright Kaplan AEC Education,
2008
Newton’s 2nd
Law

44. Copyright Kaplan AEC Education,
2008
Solution

45. Copyright Kaplan AEC Education,
2008
Work & Kinetic Energy

46. Copyright Kaplan AEC Education,
2008
Solution

47. Copyright Kaplan AEC Education,
2008
Moments of Force & Momentum

48. Copyright Kaplan AEC Education,
2008
Solution

49. Copyright Kaplan AEC Education,
2008
Solution (continued)

50. Copyright Kaplan AEC Education,
2008
Solution (continued)

51. Copyright Kaplan AEC Education,
2008
Work & Kinetic Energy

52. Copyright Kaplan AEC Education,
2008
Solution

53. Copyright Kaplan AEC Education,
2008
Solution

54. Copyright Kaplan AEC Education,
2008
Work & Kinetic Energy

55. Copyright Kaplan AEC Education,
2008
Solution

56. Copyright Kaplan AEC Education,
2008
Solution (continued)

57. Copyright Kaplan AEC Education,
2008
Work & Kinetic Energy

58. Copyright Kaplan AEC Education,
2008
Solution

59. Copyright Kaplan AEC Education,
2008
Solution (continued)