Downloaded 105 times
More Related Content
![[DL輪読会]Temporal DifferenceVariationalAuto-Encoder](https://cdn.slidesharecdn.com/ss_thumbnails/20181130new-190205051636-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DL輪読会]`強化学習のための状態表現学習 －より良い「世界モデル」の獲得に向けて－](https://cdn.slidesharecdn.com/ss_thumbnails/20181026staterepresenration-181127055206-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DL輪読会]Temporal Abstraction in NeurIPS2019](https://cdn.slidesharecdn.com/ss_thumbnails/20191115-191112082849-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DL輪読会]相互情報量最大化による表現学習](https://cdn.slidesharecdn.com/ss_thumbnails/20190913iwasawa-190913002312-thumbnail.jpg?width=640&height=640&fit=bounds)
Similar to スパース性に基づく機械学習 2章 データからの学習
スパース性に基づく機械学習 2章 データからの学習
- 1. 1章 & 2章 はじめに& データからの学習 機械学習プロフェッショナルシリーズ輪読会 ~スパース性に基づく機械学習*1~ 2016-2-10 @hagino3000 (Takashi Nishibayashi)
- 2.
- 3. 1章 はじめに • スパース性とは •まばらである事 • 多くの変数のうち殆どがゼロでごく一部だけが非ゼロ • ゲノムの個人差からの予測ケース • featureが膨大 • 現実的な仮定を置いて、少ないサンプルで推定したい • 組み合わせ爆発を防いで現実的な計算量で推定したい
- 4.
- 5.
- 6.
- 7. 2章の流れ • データから学習する、とは • 汎化 •経験誤差の最小化と過学習 • 正則化
- 8.
- 9. データから学習するとは • 訓練データ (xi,yi)i が何らかの規則に従って生成さ れている時に、データを生成する規則をなるべくよ く模倣し、再現する事 • (xi, yi) が同時確率P(x,y)から独立同一に生成されて いるという状況を考えるのが統計的機械学習 • 訓練データには無い、新しく書かれた数字を識別で きるようになることを汎化すると言う Section 2.1
- 10. 学習の評価 • データを生成する規則をどの程度よく模倣している か • 入力ベクトルxからラベルyをどの程度予測できるか →判別的なモデル • 手書き文字認識では、新しく書かれた数字を平均的 にどれだけ識別できるかを評価基準とする Section 2.1
- 11.
- 12.
- 13.
- 14. ロジスティック損失の導出 Section 2.1 2クラス分類 y∈ {-1, +1} の場合 クラス事後確率の比の対数をfとすると
- 15.
- 16. ロジスティック損失の導出 Section 2.1 二値なので q(y= +1|x) + q(y = -1|x) = 1 q(y = -1|x) = 1 - q(y = +1|x) を使って 式2.4をq(y = +1|x)について整理すると y=+1, y=-1 のケースを一つの式で表現すると
- 17.
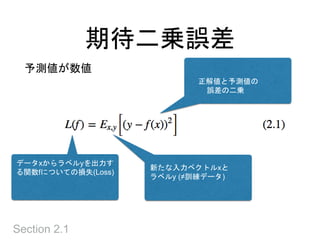
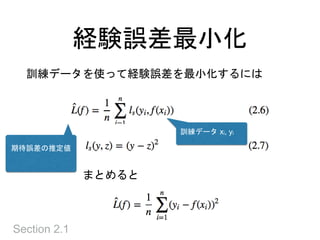
- 18. 期待誤差 • 未知の確率分布 P(x,y) に関する期待値なので、直 接評価できない • 期待誤差と呼び、訓練データで計算できる経験誤差 とは区別 • 直接計算できない → 訓練データで近似する Section 9.1
- 19.
- 20. 経験誤差最小化 Section 2.1 線形モデル f(x)= xTw + b を仮定すると L(f)を最小化するw, b 推定量 を求めるのが経験誤差最小化 誤差を正規分布とした時の最尤推定と同じ
- 21. 確率分布と損失関数 Section 2.1 • 二乗誤差、対数損失、ロジスティック損失に対する経験誤 差はいずれもそれに対応する確率モデルが存在する •確率モデル基づかない損失関数 • 0 - 1損失 • ヒンジ損失 ヒンジ損失とロジスティッ ク損失はどちらも凸関数
- 22.
- 23.
- 24.
- 25. Section 2.2 真のモデル y =100(xi - 0.2)(xi - 0.5)(xi - 0.8) + εi への当てはめ
- 26.
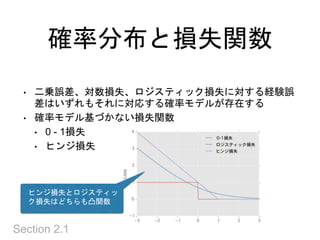
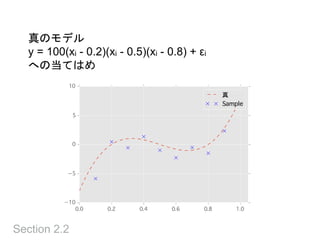
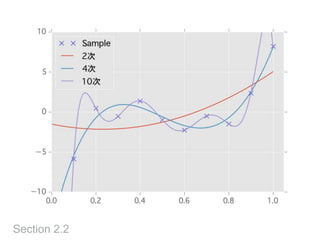
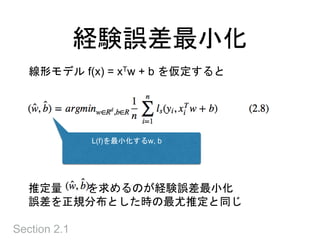
- 27. 過剰適合を防ぐ Section 2.2 • 10次の多項式で当てはめると誤差ゼロ •真の関数だけでなく、ノイズにも適合してしまった • モデルを制約するには • 多項式などの独立な基底関数の和として関数fを表現し、 その基底関数の数を小さくおさえる • 関数fの何らかのノルムを抑える • モデルを小さくしすぎると、モデル化したい関数も表現で きなくなる → 過少適合 • モデルの小ささに由来する誤差 → バイアス or 近似誤差
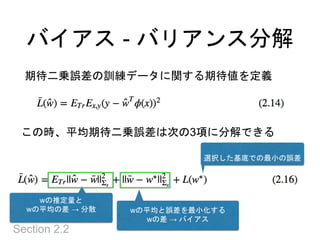
- 28. バイアス - バリアンス分解 Section2.2 期待二乗誤差の訓練データに関する期待値を定義 この時、平均期待二乗誤差は次の3項に分解できる wの推定量と wの平均の差 → 分散 wの平均と誤差を最小化する wの差 → バイアス 選択した基底での最小の誤差
- 29.
- 30. パラメータベクトルのノルム制約 Section 2.3 • 仮説集合の大きさを制御する方法 •特徴量を増やしたり減らしたりするだけではない • 同じ特徴空間であってもパラメータベクトルwをより小 さい集合から選ぶ事で分散を減らせる • ノルム
- 31.
- 32. 罰則項付き推定量 Section 2.3 誤差 +パラメータベクトルのノルム(罰則項)を最小化 正則化パラメータ この推定量は次の制約付き最小化問題と等価
- 33.
- 34. モデル選択 Section 2.4 • モデルの持つパラメータを決定したい •訓練データに対してはCを大きくすれば当てはまりは良く なってしまう → 訓練データは使えない • 検証(validation)データを使う • データを訓練用と検証用に分ける • 検証データに対する誤差を最小化する • 交差確認(cross validation) • 訓練データをK個に分割し、K-1個で学習し、残りで誤差を 評価する Kをデータと同じまで増やすとLeave-one-out
- 35.
- 36.
- 37.