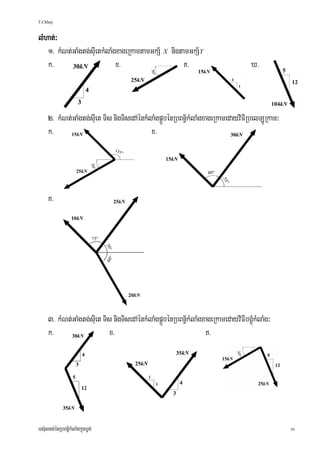
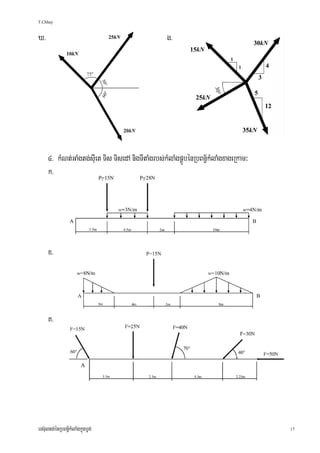
1. The resultant of two concurrent forces acting on a particle is calculated. The forces are F1 = 100 N at 30° and F2 = 140 N at 45°. 2. Using the law of cosines, the resultant is found to be 192 N at an angle of 44.8° from F1. 3. The method of components is used to analyze the coplanar force system, resolving the forces into horizontal (X) and vertical (Y) components. The resultant is verified to be 214 N at an angle of 35.9° from the X-axis.

1. T.Chhay
ers‘ultg;¬kMlaMgpÁÜb¦énRbBn§½kMlaMgkñúgbøg;
Resultants of Coplanar Force System
1> kMlaMgpÁÜbénkMlaMgBIrRbsBVKña (Resultant of two concurrent forces)
RbsinebIkMlaMgBIrRbsBVKña)anmMuEkgenaHeKGacCMnYskMlaMgTaMgBIrenaHedaykMlaMgpÁÜbmYy Edlman
tMélesIμ³
R = FX2 + FY2
nig tan θ X =
FY
FX
¬emIlrUbTI1¦
k> viFIRbelLÚRkam
kñúgkrNIEdlmMupÁúMrvagkMlaMgBIrminesμI 90 enaHkMlaMgpÁÜbkMNt;tamviFIRbelLÚRkammantMélesμI³
o
R 2 = F12 + F22 − 2 F1 F2 cos φ
ers‘ultg;énRbBn§½kMlaMgkñúgbøg; 1

2. T.Chhay
eday φ = 180 − α ⇒ cosφ = − cosα
dUcenH R = F + F + 2F F cosα
2
1
2
2
2
1 2
nig sin θ = F sin φ ¬emIlrUbTI2¦
R
1
dUcKña φ = 180 − α ⇒ sin φ = sin α
dUcenH sin θ = F sin α
R
1
F1 sin α
⇒ θ = arcsin
R
Edl α CamMupÁúMrvagkMlaMgTaMgBIr F nig F . 1 2
cMNaMfa RbBn§½kMlaMgRbsBVkñúgbøg; ExSskmμrbs;kMlaMgpÁÜb EtgmancMnuccab;Rtg;kEnøgRbsBVKñaén
RbBn§½kMlaMgenaH. dUcenH TItaMgrbs;kMlaMgpÁÜbEtgEtRtUv)andwg ehIyGVIEdlcaM)ac;RtUvkaredaHRsayKW
GaMgtg;sIueténkMlaMg Tis nigTisedArbs;va.
]TahrN_³ kMNt;GaMgtg;sIuet Tis nigTisedA énkMlaMgpÁÜbrvagkMlaMgBIr F nig F RbsBVKñakñúgbøg;Rtg;cMnuc
1 2
0 dUcbgðajkñúgrUbTI3. GaMgtg;sIuetrbs;kMlaMgTaMgBIrmantMél F = 100 N nig F = 140 N . kMlaMg F
1 2 1
pÁúMCamYy GkS½ X )anmMu 30 enAEpñkxagelI ÉkMlaMg F pÁúMCamYyGkS½ X )anmMu 45 enAEpñkxageRkam.
o
2
o
ers‘ultg;énRbBn§½kMlaMgkñúgbøg; 2

3. T.Chhay
dMeNaHRsay³
kMNt;mMupÁúMrvagkMlaMgTaMgBIr F nig F
1 2
α = α 1 + α 2 = 30 o + 45 o = 75 o
kMNt;mMu φ
φ = 180 o − α = 180 o − 75 o = 105 o
kMNt;GaMgtg;sIueténkMlaMgpÁÜb
R 2 = F12 + F22 − 2 F1 F2 cos φ = 100 2 + 140 2 − 2 × 100 × 140 × cos105 o
⇒ R = 192 N
mMuR)ab;Tis rbs;kMlaMgpÁÜbCamYykMlaMg F 1
R F
= 2
sin φ sin θ
F2 sin φ 140 × sin 105 o
⇒ θ = arcsin = arcsin = 44.8 o
R 192
dUcenH mMuR)ab;Tisrbs;kMlaMgpÁÜbCamYyGkS½ X
θ x = θ − α 1 = 44.8 o − 30 o = 14.8 o
mMuenaHmanTisRsbtamRTnicnaLika. dUcenHTisrbs;kMlaMgpÁÜb cuHeRkameTAsþaM.
ers‘ultg;énRbBn§½kMlaMgkñúgbøg; 3

4. T.Chhay
x> viFIbgÁúMkMlaMg
kñúgkarkMNt;kMlaMgpÁÜb énRbBn§½kMlaMgRbsBV eRkABIviFIRbelLÚRkam eKenAmanviFImYyeTotehAfaviFI
bgÁúMkMlaMg (method of components). viFIenHCaviFImYyEdlmanlkçN³TUeTAkñúgkarkMNt;kMlaMgpÁÜb.
viFIbgÁúMkMlaMgCaviFIEdleRbIRbBn§½kUGredaenEkg X − Y . xageRkamCaviFIsaRsþkñúgkarGnuvtþviFIenH³
- KNnaplbUknBVn<énbgÁúMkMlaMgTaMgGs;tamGkS½ X (∑ F = R ) X X
- KNnaplbUknBVn<énbgÁúMkMlaMgTaMgGs;tamGkS½ Y (∑ F = R ) Y Y
- KNnaGaMgtg;sIuetkMlaMgpÁÜbtamrUbmnþ R = R + R 2
X
2
Y
∑F
- KNnamMuR)ab;TisrvagkMlaMgpÁÜbCamYyGkS½ X tamrUbmnþ tan θ = R = ∑ FR
X
Y Y
X X
]TahrN_³ kMNt;GaMgtg;sIuet Tis nigmMuR)ab;TisCamYYyGkS½ X rbs;kMlaMgpÁÜb R dUcbgðajkñúgrUbTI4.
dMeNaHRsay³
1> bgÁúMkMlaMgpÁÜbtamGkS½ X / R esμInwgplbUknBVnþénbgÁúMkMlaMg F nig F tamGkS½ X
X 1 2
12
R X = ∑ FX = F1 X + F2 X = 350 − 300 × cos 60 o
13
R X = +173.1N → ¬tMél R viC¢man mann½yfaTisedArbs;kMlaMgeTAsþaM¦
X
2> bgÁúMkMlaMgpÁÜbtamGkS½ Y / R esμInwgplbUknBVnþénbgÁúMkMlaMg F nig F tamGkS½ Y
Y 1 2
ers‘ultg;énRbBn§½kMlaMgkñúgbøg; 4

5. T.Chhay
5
RY = ∑ FY = F1Y + F2Y = −350 + 300 × sin 60 o
13
RY = +125.2 N ↑ ¬tMél R viC¢man mann½yfaTisedArbs;kMlaMgeTAelI¦
Y
3> kMlaMgpÁÜbén R nig R KW R dUcbgðajkñúgrUbTI5
X Y
R = R X + RY
2 2
⇒ R = 173.12 + 125.2 2 = 214 N
TisedArbs;kMlaMgpÁÜb eTAelInigxagsþaM
4> mMuR)ab;Tisrbs;kMlaMgpÁÜbeFobnwgGkS½ X
RY 125.2
θ = tan −1 = tan −1 = 35.9 o
RX 173.1
cMNaM³ sMrab;RbBn§½kMlaMgeRcInelIsBIBIr RbsBVKña b¤minRbsBVKña viFIbgÁúMkMlaMgCaviFIgayRsYl kñúgkarkMNt;;
kMlaMgpÁÜbénRbBn§½kMlaMgenaH.
2> m:Um:g;énkMlaMg (Moment of forces)
ers‘ultg;énRbBn§½kMlaMgkñúgbøg; 5

6. T.Chhay
kMlaMgEdlmanGMeBIeTAelIGgÁFatumYyEdlenAes¶óm GgÁFatu enaHnwgmanclnatamBIrebobxusKña
mü:ag vaGacRtUvrMkil (translation) eTAelIb¤eTAeRkam eTAsþaMb¤eTAeqVg nigmü:ageTot vaGacRtUvvil
(rotation) CMuvijExS b¤GkS½NamYy. dUckñúgrUbTI6 (a) eRkamGMeBIénkMlaMg P EdlGnuvtþmkelIGgÁFaturwg
ÉksN§an Rtg;cMnuckNþal enaHGgÁFatunwgrMkileTAmux EdlRKb;cMnucTaMgGs; rbs;vamanKMlatesμI²Kña.
RbsinebIkMlaMgdEdl manGMeBImkelIGgÁFatuRtg;cMnucepSgeRkABIcMnuckNþal enaHGgÁFatunwgmanclnapSM
Kñarvag rMkilnigbgVilCamYyKña ¬rUbTI6(b)¦. EtRbsinebIeK eKcab;GgÁFatuenaH Rtg;cMnuc A eGayCab;edIm,I
kMueGayvarMkileTAmuxenaH vanwgekItmanEtkarbgVilEtmYyKt; ¬rUbTI6(c)¦.
GMeBIénkMlaMgEdleFVIeGayGgÁFatumYyGacvil)anRtUv)anKeGayeQμaHfam:Um:g;.
m:Um:g;RtUv)ankMNt;tamrUbmnþxageRkam³
M = ± Fd
Edl - m:Um:g;énkMlaMg ( N .m)
M
F - kMlaMg ( N )
d - cMgayEkgrvagkMlaMgnwgGkS½ b¤cMnuc ¬édXñas;¦ (m)
eRkamGMeBIénkMlaMg GgÁFatumYymanclnavilRsbTisénRTnicnaLika RtUv)aneKsnμt;eGaym:Um:g;man
tMélGviC¢manpÞúymkvij vanwgmansBaØabUkenAeBlNaEdlGgÁFatuvilRcasTisénRTnicnaLika ¬rUbTI7¦.
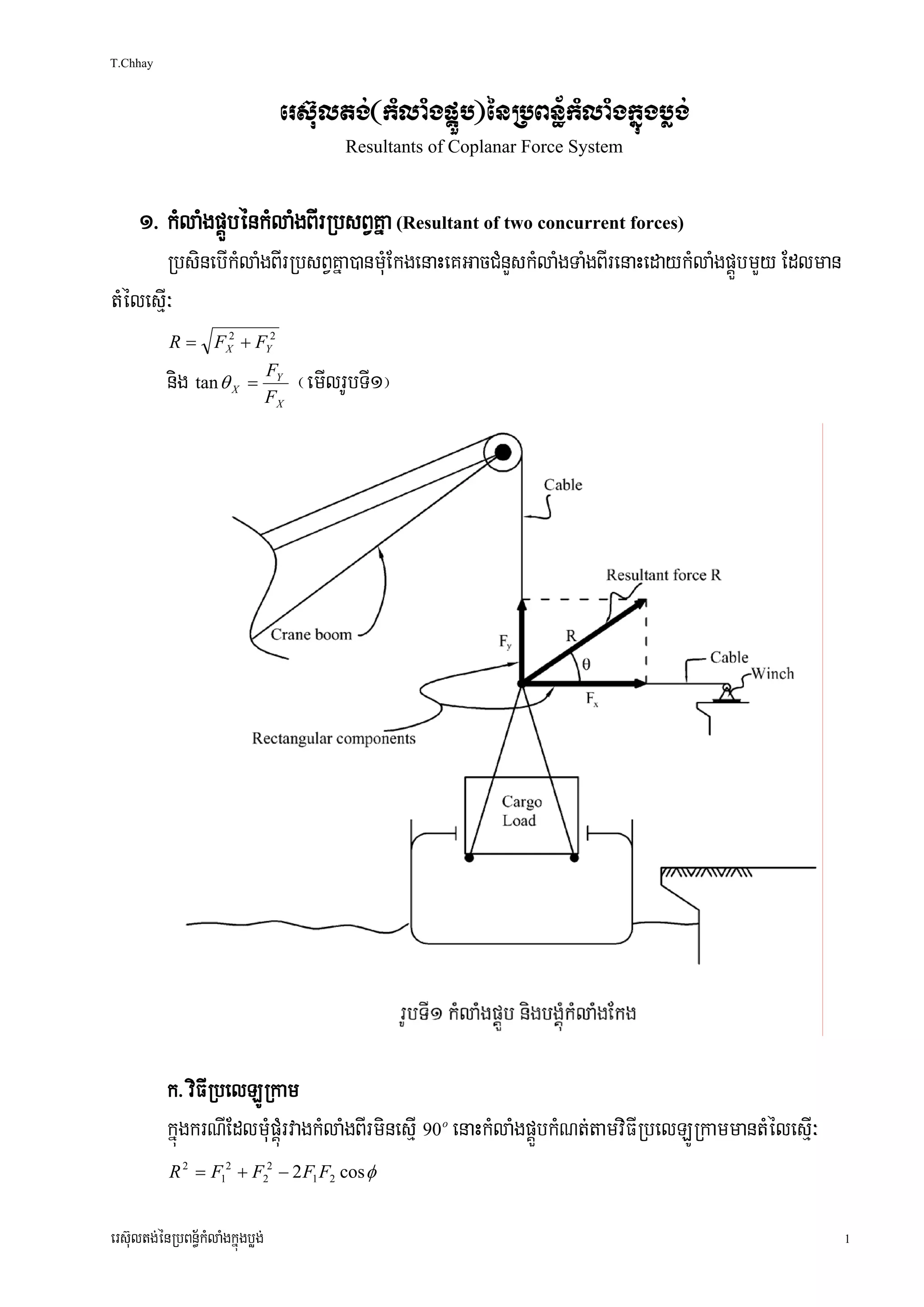
]TahrN_³ kMlaMgRbsBVkñúgbøg;bImanGMeBImkelIGgÁFatumYyRtg;cMnuc A dUcbgðajkñúgrUbTI8.
k> kMNt;m:Umg;énkMlaMgnImYy²eFobcMnuc O.
x> kMNt;plbUkBiCKNiténm:Um:g;énkMlaMgTaMgbIeFobcMnuc O nigkMNt;TisénrgVil.
ers‘ultg;énRbBn§½kMlaMgkñúgbøg; 6

7. T.Chhay
dMeNaHRsay³
k> kMNt;m:Umg;énkMlaMgnImYy²eFobcMnuc O
edaycMnuc O sßitenAelIExSskmμénkMlaMg F dUcenHm:U:m:g;énkMlaMg F esμIsUnü.
1 1
eRBaHkMlaMg F min)aneFVIeGayGgÁFatuvileFobcMnuc O eT.
1
m:Um:g;énkMlaMg F RtUv)anKNnatamrUbmnþ
2
M 2 = F2 d = +75 × 5 = +375 N .m
m:Um:g;enHmansBaØaviC¢manedaysarTisénm:Um:g;RcasTisénRTnicnaLika
m:Um:g;énkMlaMg F RtUv)anKNnatamrUbmnþ
2
M 3 = F3 d = −60 × 5 × sin 30 o = −150 N .m
edaysarvavilRsbRTnicnaLika dUcenHm:Um:g;RtUvmansBaØadk.
x> kMNt;plbUkBicKNiténm:Um:g;énkMlaMgTaMgbIeFobcMnuc O nigkMNt;TisénrgVil
∑ M = 0 + 375 − 150 = +225 N .m
m:Um:g;mansBaØabUk dUcenHrgVilmanTisRcasRTnicnaLika.
3> eKalkarN_rbs;m:Um:g;-RTwsþIbTv:arIjú:g (Principle of moments-Varignon’s theorem)
m:Um:g;pÁÜb b¤m:Um:g;énkMlaMgpÁÜbénRbBn§½kMlaMgmYy eFobcMnucmYymantMélesμInwgplbUkBiCKNitén
m:Um:g;rbs;bgÁúMkMlaMgnImYy²énRbBn§½enaH eFobnwgcMnucenaH.
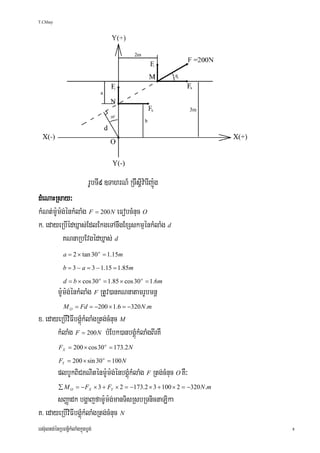
]TahrN_³ kMNt;m:Um:g;énkMlaMg F = 200 N eFobcMnuc O EdlsßitenAelIbøg; X − Y ¬rUbTI9¦.
edayeRbInUvbec©keTsxageRkamcUrKNna³
k> edayeRbIédXñas;EdlEkgeTAnwgExSskmμénkMlaMg
x> edayeRbIviFIbgÁúMkMlaMgRtg;cMnuc M
K> edayeRbIviFIbgÁúMkMlaMgRtg;cMnuc N
ers‘ultg;énRbBn§½kMlaMgkñúgbøg; 7

8. T.Chhay
dMeNaHRsay³
kMNt;m:Um:g;énkMlaMg F = 200 N eFobcMnuc O
k> edayeRbIédXñas;EdlEkgeTAnwgExSskmμénkMlaMg d
KNnaRbEvgédXñas; d
a = 2 × tan 30 o = 1.15m
b = 3 − a = 3 − 1.15 = 1.85m
d = b × cos 30 o = 1.85 × cos 30 o = 1.6m
m:Um:g;énkMlaMg F RtUv)anKNnatamrUbmnþ
M O = Fd = −200 × 1.6 = −320 N .m
x> edayeRbIviFIbgÁúMkMlaMgRtg;cMnuc M
kMlaMg F = 200 N bMEbk)anbgÁúMkMlaMgBIrKW
FX = 200 × cos 30 o = 173.2 N
FY = 200 × sin 30 o = 100 N
plbUkBiCKNiténm:Um:g;énbgÁúMkMlaMg F Rtg;cMnuc O KW³
∑ M O = − FX × 3 + FY × 2 = −173.2 × 3 + 100 × 2 = −320 N .m
sBaØadk bgðajfam:Um:g;manTisRsbRTnicnaLika
K> edayeRbIviFIbgÁúMkMlaMgRtg;cMnuc N
ers‘ultg;énRbBn§½kMlaMgkñúgbøg; 8

9. T.Chhay
tameKalkarN_énviFIrMkil eK)anbgÁúMkMlaMg F Rtg;cMnuc M mantMélesμIbgÁúMkMlaMg F Rtg;cMnuc N .
edaycMnuc O sßitelIExSskmμénbgÁúMkMlaMg F dUcenHm:Um:g;énkMlaMg F esμIsUnü. dUcenHplbUkBiC
Y Y
KNiténm:Um:g;énkMlaMg F esμI³
∑ M O = − FX b = −173.2 × 1.85 = −320 N .m
4> kMlaMgpÁÜbénRbBn§½kMlaMgRsb (Resultants of parallel force systems)
RbBn§½kMlaMgRsb CaRbBn§½kMlaMgEdlExSskmμénkMlaMgnImYy² kñúgRbBn§½manTisRsbKña.
ExSskmμénkM -laMgpÁÜbénRbBn§½kMlaMgRsb manTisRsbnwgRbBn§½kMlaMgenaH. GaMgtg;sIuet TisedA
énkMlaMgpÁÜbRtUv)ankMNt; edayplbUkBiCKNiténRbBn§kMlaMgenaH. ¬rUbTI10¦
R = ∑ FY = F1 + F2 + ... + Fn
cMENkÉTItaMgénExSskmμrbs;kMlaMgpÁÜbRtUv)anedaHRsayedayeRbIeKalkarN_m:Um:g; RTwsþIbTv:arIj:úg.
∑ M O = R.x = F1 .x1 + F2 .x 2 + ... + Fn .x n
F .x + F2 .x 2 + ... + Fn .x n
⇒x= 1 1
R
∑M
b¤x=
R
]TahrN_³ kMNt;kMlaMgpÁÜbénRbBn§½kMlaMgRsb dUcbgðajkñúgrUbTI11 EdlmanGMeBIelIFñwmedk AB mYy.
kMlaMgTaMgGs;suT§EtbBaÄr. edayecalTMgn;pÞal;rbs;Fñwm.
ers‘ultg;énRbBn§½kMlaMgkñúgbøg; 9

10. T.Chhay
dMeNaHRsay³
GaMgtg;sIuetkMlaMgpÁÜbénRbBn§½kMlaMgRsbesμInwgplbUlBiCKNiténkMlaMgbBaÄr
edaysnμt;TisedAeLIgelI mansBaØaviC¢man
R = ∑ FY = −25 − 15 + 10 − 20 = −50 N ↓
TItaMgrbs;kMlaMgpÁÜb RtUv)ankMNt;edayplbUkBiCKNiténm:Um:g;énkMlaMgTaMgGs;eFobcMnuc A
∑ M A = −15 × 3 + 10 × 9 − 20 × 14 = −235 N .m
∑ M A − 235
⇒x= = = 4.7m
R − 50
dUcenHkMlaMgpÁÜnénRbBn§½kMlaMgRsb mantMél 50 N manTisbBaÄr TisedAcuHeRkam
nigmanTItaMgcMgay 4.7m BI cMnuc A .
5> kMlaMgpÁÜbénbnÞúkBRgay (Resultants of distributed load)
ers‘ultg;énRbBn§½kMlaMgkñúgbøg; 10

11. T.Chhay
bnÞúkBRgay KWCakMlaMgEdlmanGMeBIelIGgÁFatu edayBRgayelIÉktaépÞ b¤rayelIÉktaRbEvg.
bnÞúkBRgayRtUv)anEckCaBIrKW³ bnÞúkBRgayesμI (uniformly distributed load) CabnÞúkEdlBRgay
edayGaMgtg;sIuetesμI²KñaelIÉktaRbEvgnig bnÞúkBRgayminesμI (nonuniformly distributed load)
¬rUbTI12¦. xñatrbs;bnÞúkBRgayRtUv)anKitCa N m .
bnÞúkpÁÜbénbnÞúkBRgay CaGaMgetRkalénGaMgtg;sIuettam RbEvgEdlvaBRgayelI b¤CaRkLaépÞén
bnÞúkBRgayenaH¬rUbTI13¦. bnÞúkpÁÜbenaHmanGMeBIkat;tamTIRbCMuTMgn; énragFrNImaRtrbs;bnÞúk BRgay
enaH.
R = ∫ q ( x )dx
b
a
b
∫ q(x ).xdx
x= a
R
ers‘ultg;énRbBn§½kMlaMgkñúgbøg; 11

12. T.Chhay
]TahrN_³ kMNt;GaMgtg;sIuet nigTItaMgrbs;kMlaMgpÁÜb R énRbBn§½kMlaMgRsbdUcbgðajkñúgrUbTI14.
RbBn§½kMlaMgmanGMeBIelIFñwmedk AB . kMlaMgTaMgGs;manTisbBaÄr ehIyTMgn;pÞal;rbs;FñwmRtUv)anecal.
dMeNaHRsay³
kMlaMgpÁÜb W énbnÞúkBRgayesμI w = 2 N / m EdlrayelIRbEvg 14m esμInwg
W = 2 × 14 = 28 N
ehIykMlaMgpÁÜbenHRtUvCMnYsedaykMlaMgcMcMnucEdlmanGMeBIkat;tamTIRbCMuTMgn;
b¤esμInwgBak;kNþalRbEvgEdlva )anBRgayelI ¬sMrab;bnÞúkBRgayragctuekaNEkg¦.
kMlaMgpÁÜbénRbBn§½kMlaMgRsb
R = ∑ Fy = −3 − 8 − 28 = −39 N
plbUkm:Um:g;énRbBn§½kMlaMgRsbeFobcMnuc A
∑ M A = −3 × 5 − 8 × (5 + 7) − 28 × (5 + 7 + 4 + 7) = −755 N
TItaMgrbs;kMlaMgpÁÜbeFobcMnuc A
∑ M A − 755
x= = = 19.4m
R − 39
6> kMlaMgbgVil (Couple)
kalNakMlaMgBIrminenAelITMrEtmYy manExSskmμRsbKña GaMgtg;sIuetesμIKña b:uEnþmanTisedApÞúyKña
vabegáIt)ankrNIBiessmYyEdleKeGayeQμaHfa kMlaMgbgVil. ¬rUbTI15¦
ers‘ultg;énRbBn§½kMlaMgkñúgbøg; 12

13. T.Chhay
C = ± F .d
lkçN³rbs;kMlaMgbgVilRtUv)ankMNt;cMNaMdUcxageRkam³
- kMlaMgbgVilminTak;TgcMnucNamYyrbs;bøg;eLIy
- GaMgtg;sIueténkMlaMgpÁÜbrbs;kMlaMgbgVilesμIsUnü
- kMlaMgbgVilpÁÜbmantMélesμIplbUkBiCKNiténkMlaMgbgVilTaMgGs;
- kMlaMgbgVilmansBaØabUk enAeBlNaEdlvaeFVIeGayGgÁFatumYyvilRcasRTnicnaLika
]TahrN_³
kMNt;GaMgtg;sIueténm:Um:g;énkMlaMgBIrRsbKñadUcbgðajkñúgrUbTI16. edayeFobnwg
k> cMnuc O
x> cMnuc B
ers‘ultg;énRbBn§½kMlaMgkñúgbøg; 13

14. T.Chhay
dMeNaHRsay³
edaysarkMlaMgTaMgBIrmanGaMgtg;sIuetesμIKña TisedApÞúyKña dUcenHvabegáIt)ankMlaMgbgVilmYy
C = 100 × 4 = +400 N .m
KNnaGaMgtg;sIueténplbUkm:Um:g;eFobcMnuc O
∑ M o = −100 × 2 + 100 × 6 = +400 N .m
KNnaGaMgtg;sIueténplbUkm:Um:g;eFobcMnuc B
∑ M A = +100 × 7 − 100 × 3 = +400 N .m
cMNaM³ eyIgGacCMnYskMlaMgmYyEdlmanGMeBIRtg;cMnuc A edaykMlaMgmYyEdlmanGaMgtg;sIuetesμIKña
TisedAdUcKña ExSskmμRsbKña Rtg;cMnuc B edayRKan;EtbEnßmkMlaMgbgVilmYyEdlmantMélesμIplKuNrvag
kMlaMgenaHCamYycMgayrvagBIcMnuc A dl;cMnuc B . ¬rUbTI17¦
7> kMlaMgpÁÜbénRbBn§½kMlaMgminRbsBVkñúgbøg; (Resultant of no concurrent force system)
GaMgtg;sIuet Tis TisedArbs;kMlaMgpÁÜbénRbBn§½kMlaMgminRbsBVkñúgbøg; RtUv)anKNnadUckrNIRbBn§½
kMlaMgRbsBVkñúgbøg;Edr edayeRbInUvRbBn§½kUGredaen X − Y nigeRbInUvplbUkBiCKNiténbgÁúMkMlaMgtamGkS½
X nigGkS½ Y . ehIyeRbIpleFobénplbUkm:Um:g;énkMlaMgeFobcMnucNamYyelIkMlaMgpÁÜbenaH edIm,IkMNt;TI
taMgrbs;kMlaMgpÁÜbenaH.
]TahrN_³
kMNt;GaMgtg;sIuet Tis TisedA nigTItaMgrbs;kMlaMgpÁÜbénRbBn§½kMlaMgminRbsBVkñúgbøg;dUcbgðajkñúgrUbTI18.
ers‘ultg;énRbBn§½kMlaMgkñúgbøg; 14

15. T.Chhay
dMeNaHRsay³
snμt;TisedArbs;kMlaMg eTAelI nigeTAsþaMmansBaØaviC¢man dUcTisedArbs;GkS½ X nigGkS½ Y Edr.
kMNt;kMlaMgpÁÜbénbgÁúMkMlaMgtamGkS½ X
RX = ∑ FX = +10 cos 60o − 30 cos 75o − 40 cos 45o − 50 = −81N ←
kMNt;kMlaMgpÁÜbénbgÁúMkMlaMgtamGkS½ Y
RY = ∑ FY = −10 sin 60o − 20 − 30 sin 75o − 40 sin 45o = −85.9 N ↓
kMNt;kMlaMgpÁÜbénbgÁúMkMlaMgTaMgBIr
R = RX + RY =
2 2
(− 81)2 + (− 85.9)2 = 118.1N
kMNt;muMR)ab;TiseFobGkS½ X
RY − 85.9
θ X = arctan = arctan = 46.7 o
RX − 81
kMNt;plbUkm:Um:g;eFobcMnuc O
∑ M o = −20 × 4 − 30 × sin 75o × 7 − 40 × sin 45o × 12 = −622 N .m
kMNt;TItaMgkMlaMgpÁÜbeFobcMnuc O
∑ M o − 622
x= = = 7.24m
RY − 85.9
ers‘ultg;énRbBn§½kMlaMgkñúgbøg; 15

16. T.Chhay
lMhat;³
1> kMNt;GaMgtg;sIuetkMlaMgxageRkamtamGkS½ X nigtamGkS½ Y
k> x> K> X>
2> kMNt;GaMgtg;sIuet Tis nigTisedAénkMlaMgpÁÜbénRbBn§½kMlaMgxageRkamedayviFIRbelLÚRkam³
k> x>
K>
3> kMNt;GaMgtg;sIuet Tis nigTisedAénkMlaMgpÁÜbénRbBn§½kMlaMgxageRkamedayviFIbgÁúMkMlaMg³
k> x> K>
ers‘ultg;énRbBn§½kMlaMgkñúgbøg; 16

17. T.Chhay
X> g>
4> kMNt;GaMgtg;sIuet Tis TisedA nigTItaMgrbs;kMlaMgpÁÜbénRbBn§½kMlaMgxageRkam³
k>
x>
K>
A
ers‘ultg;énRbBn§½kMlaMgkñúgbøg; 17