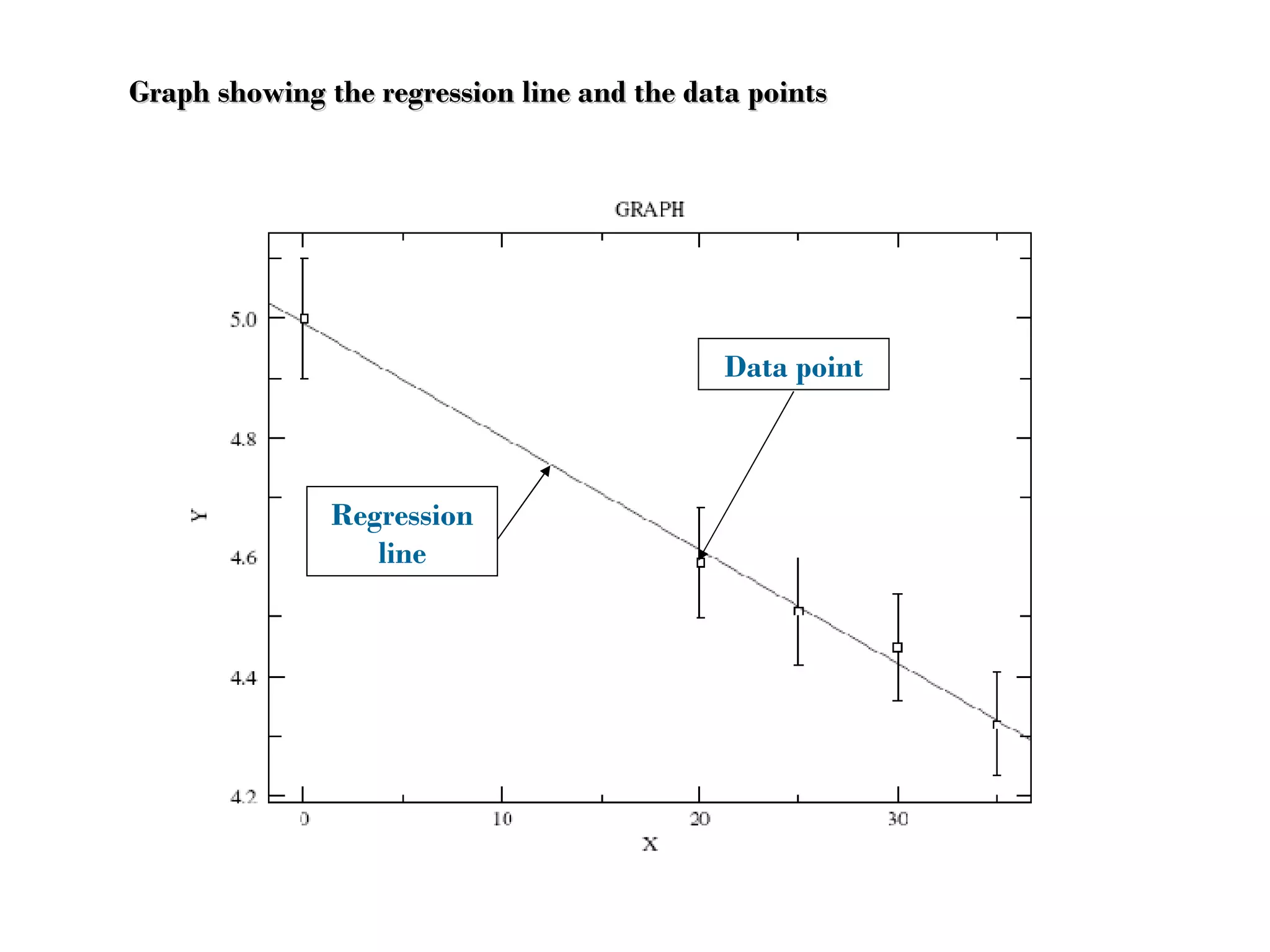
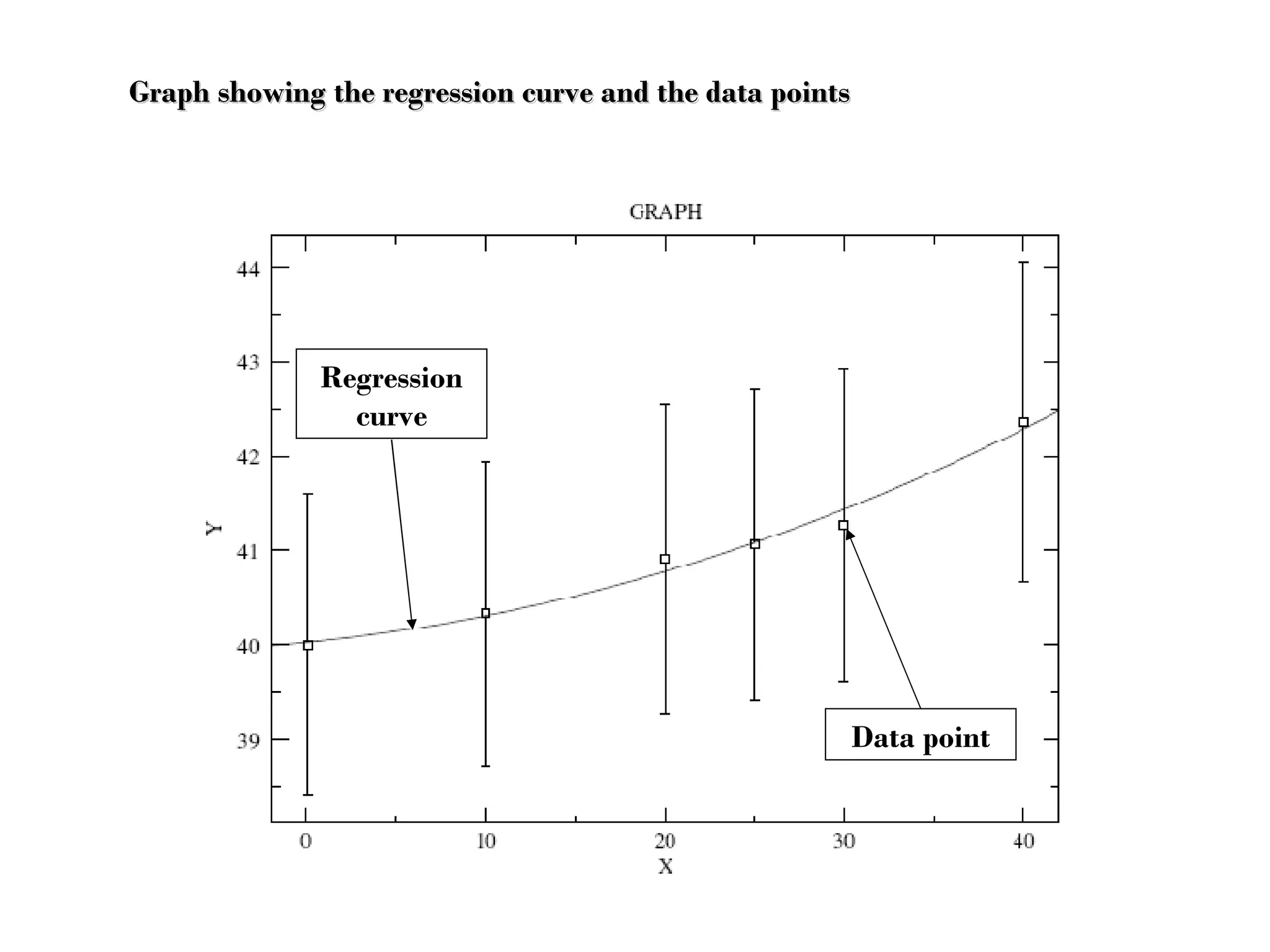
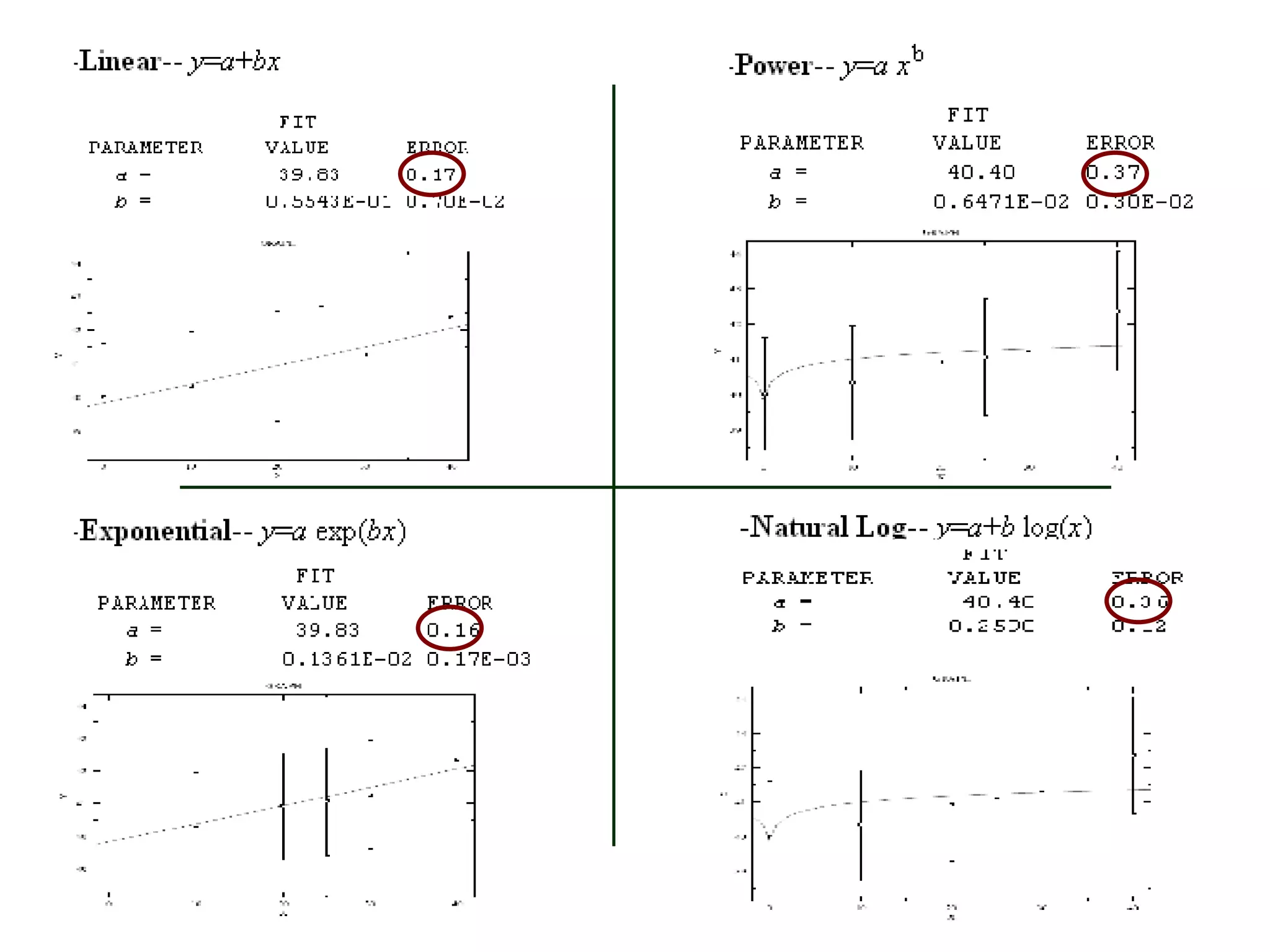
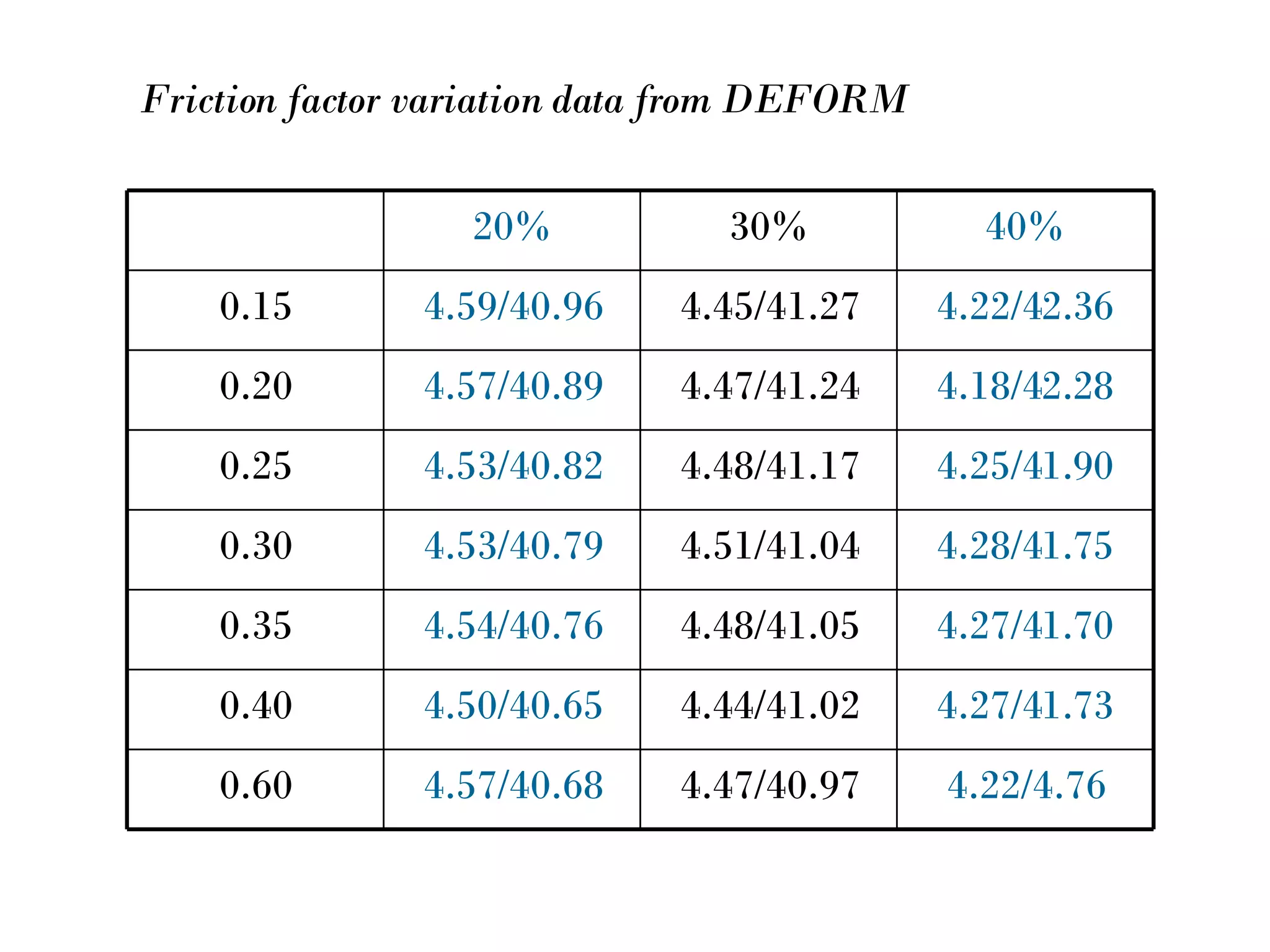
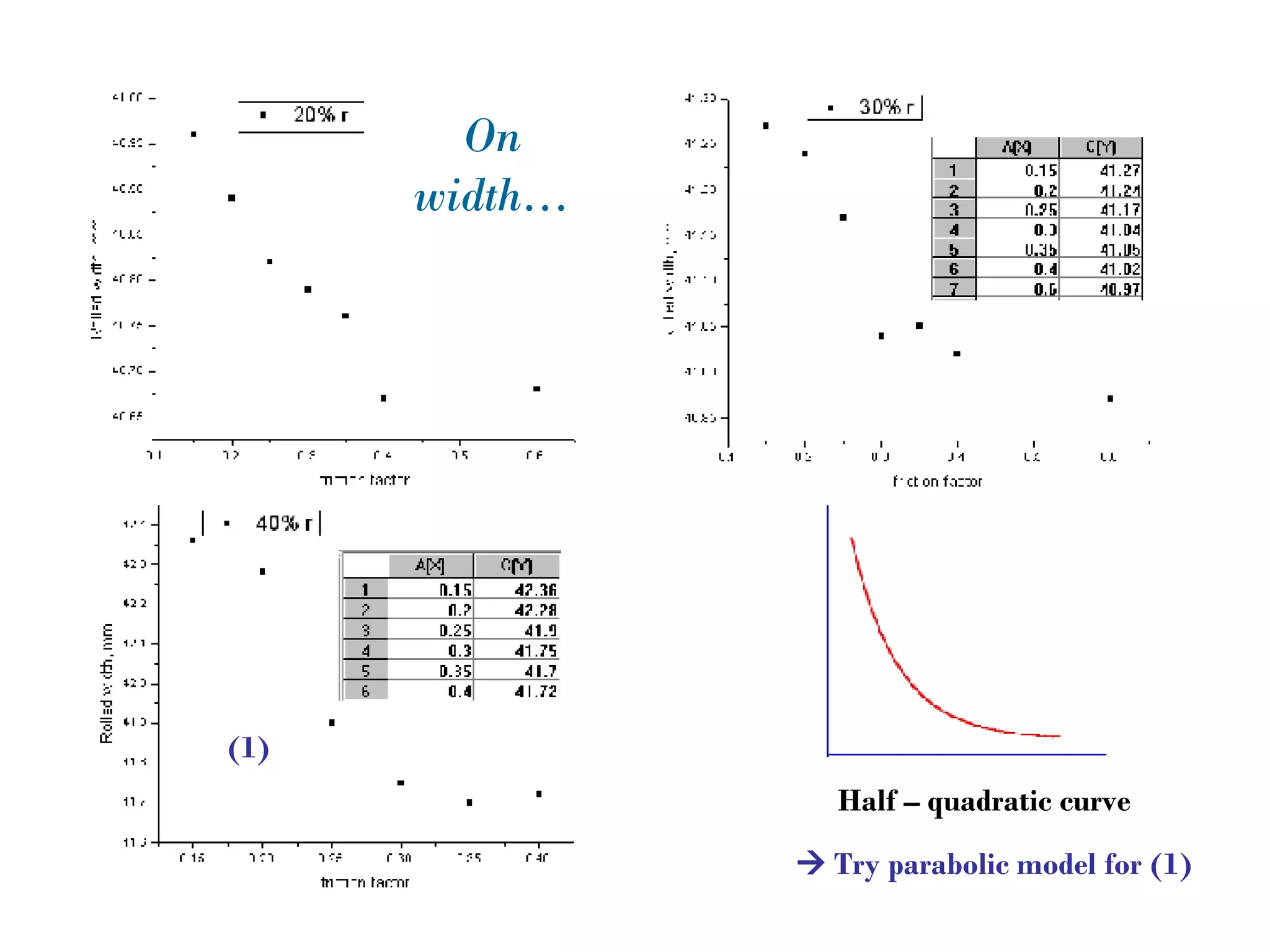
The document discusses using mathematical functions to model relationships between input and output variables in a rolling simulation. A linear model was found to accurately predict central height from thickness reduction with less than 1% error. A quadratic model also accurately predicted spread from thickness reduction with less than 1% error. Friction was found to not significantly affect central height, and a quadratic model described the relationship between spread and friction with under 1% error. Further modeling of additional variables is suggested.

1. Treating simulation data with mathematical functions using chi-square technique **…formulas achieved by using Chi - square based Java applets on http://csbsju.edu *…relationship btw outputs ( filling,spread ) and inputs ( thickness red.,friction,…)

2. Thickness reduction ( r ) variation Rolling model Filling factor = H 1 – t (H 1 = central height)

3. Fixed condition with: friction 0.15; sample width 40mm, thickness 5mm, groove 10mm and 20 degrees. 0.00 40.00 5.00 0 1.22 42.36 4.22 40 1.07 41.52 4.32 35 0.95 41.27 4.45 30 0.76 41.06 4.51 25 0.59 41.03 4.59 20 0.24 40.33 4.74 10 Filling factor (as drawn) S (mm) spread H r (mm) (central) Thickness reduction,%

4. Other fixed conditions, relationship btw Hr and r (thickness red.) Drawn with Origin 7.0 from simulation results The central (max) height

5. Linear model : y = a + bx ( http://www.physics.csbsju.edu/stats/WAPP.html ) Hr = 4.992 – 0.019r Test with r = 40  Hr = 4.992 – 0.019 x 40 = 4.232 Measured H r (40%) = 4.22 mm  error (relative) = (4.232 – 4.22)/4.22 = 0.28% Test with r = 10  Hr = 4.992 – 0.019 x 10 = 4.80. error = (4.8 – 4.74)/4.74 = 1.25%

6. Graph showing the regression line and the data points Regression line Data point

7. Filling factor and thickness reduction

8. Rolled width vs thickness reduction Plotted with Origin

9. Quadratic model : y = a + bx + cx 2 ( http://www.physics.csbsju.edu/cgi-bin/stats/WAPP ) Sr = 40.03 + 0.01862r + 0.0009461r 2 Test with r = 35  Sr = 40.03 + 0.01862x35 + 0.0009461x35 2 = 41.84 Measured S r (35%) = 4.1.52 mm  error (relative) = (41.84 – 41.52)/41.52 = 0.77%

10. Graph showing the regression curve and the data points Regression curve Data point

12. Friction factor ( m ) variation

13. Friction factor variation data from DEFORM 4.22/4.76 4.47/40.97 4.57/40.68 0.60 4.27/41.73 4.44/41.02 4.50/40.65 0.40 4.27/41.70 4.48/41.05 4.54/40.76 0.35 4.28/41.75 4.51/41.04 4.53/40.79 0.30 4.25/41.90 4.48/41.17 4.53/40.82 0.25 4.18/42.28 4.47/41.24 4.57/40.89 0.20 4.22/42.36 4.45/41.27 4.59/40.96 0.15 40% 30% 20%

14. Not significant effect on central height

15.  Try parabolic model for (1) (1) On width… Half – quadratic curve

16. Sr = 43.61 – 10.48m + 14.36m 2 Test with m = 0.20 Sr = 43.61 – 10.48x0.2 + 14.36x0.04) = 42.09 Error = (42.28 – 42.09)/42.09 = 0.45%

17. Quadratic graph

18. Central height & filling vs thickness reduction relationship can be treated with linear function Spreading vs thickness reduction can be well treated with quadratic relationship Friction does not affect central height Spread vs friction can be described by a quadratic function Upcoming: thickness, width, vacancy, inclined angle ,… Conclusions

19. Appendix

20. Appendix