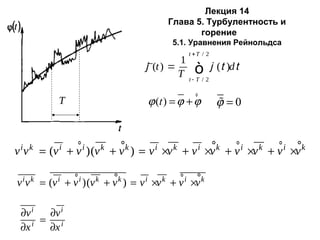
Документ представляет собой лекцию, в которой рассматриваются аспекты турбулентности и горения, включая уравнения и модели, такие как k-ε модель. Обсуждаются различные формулы, связанные с уравнениями движения и переноса, а также аналитические подходы к моделированию химических реакций и тепловых процессов в горении. Включены ссылки на исследования и работы, касающиеся детонации и других аспектов горения.

1. Лекция 14
Глава 5. Турбулентность и
горение
5.1. Уравнения Рейнольдса
1
j (t ) =
T
T
t +T / 2
ò
j ( t )d t
°
ϕ (t ) = ϕ + ϕ
%
ϕ =0
t- T / 2
°
°
°
°
° °
v i v k = (v i + v i )(v k + v k ) = v i ×v k + v i ×v k + v i ×v k + v i ×v k
°
°
° °
v i v k = (v i + v i )(v k + v k ) = v i ×v k + v i ×v k
∂v i
∂v i
i =
∂x
∂x i

2. ∂v i
∂v i v j
∂
ρ
+ρ
= i
∂t
∂x j
∂x
 π 11 π 12

 π 21 π 22
 π 31 π 32


 ∂v i ∂v j
i j 
 pδij + µ  j + i − ρ v v ÷÷
∂x

 ∂x

( )

°1 2
 −ρ v
π 13  

° °
π 23  =  − ρ v 2 v 1

π 33  

° °
− ρv 3v1


 ∂v i ∂v j 
ρ v v = µt  j + i ÷
∂x 
 ∂x
° °
− ρ v 1v 2
( )
°
−ρ v2
2
° °
− ρv 3v 2
° ° 
− ρ v 1v 3 

° °
− ρv 2v 3 

°3 2 
−ρ v


( )
i j
(
1 ° 1 ° 1 °2 °2 ° 3 ° 3
K = v v +v v +v v
2
)
°i °i
°i
k
%
∂K
∂  k p
°k π + v k v v  = −π ∂v − τ ∂v
°
k ∂K
i
+v
÷
ik
ik
k +
k  v ρ − v π ik + v ik

∂t
2 ÷
∂x
∂x
∂x k
∂x k



3. τ ik
°
°
µ  ∂v i ∂v k 
=  k + i ÷
ρ  ∂x
∂x 
°
°
°
°
°
°
 ∂v i ∂v k  ∂v k ν  ∂v i ∂v k
∂v i
τ ik k = ν  k + i ÷ i =  k + i
2  ∂x
∂x  ∂x
∂x
∂x
 ∂x
°k ∂v i 2
°
ν  ∂v
=  i + k ÷ >0
2  ∂x
∂x 
°
°
°
°
 ∂v i ν  ∂v k ∂v i  ∂v k
÷ k +  i + k ÷ i =
2  ∂x
∂x  ∂x
 ∂x

4. 5.2. Модель Прандтля
τ ik
∂v 1
° °
= − ρ v 1v 2 = µt 2
∂x
∂v 1
µt = l 2
∂x 2
∂v 1 ∂v 1
τ = l2
∂x 2 ∂x 2
∂v 1
l =κ 2
∂x
∂2v 1
∂( x
)
2 2
Формула Кармана

5. 5.3. Кε – модель турбулентности
Коэффициент турбулентного переноса
nt = C mK 2 / e
Уравнение энергии турбулентных пульсаций
∂v j
∂ρ K
r
∂  ν t ∂K 
+ div( ρvK ) =
− ρε
ρ
÷ + τ t ,ij
∂t
∂x i  σ k ∂x i 
∂x i
Уравнение диссипации турбулентных пульсаций
∂ρε
r
∂
+ div( ρv ε ) =
∂t
∂x i
 ρ ν t ∂ε  + ε  C τ ∂v j − C ρε 
÷
 σ ∂x ÷ K  1ε t ,ij ∂x
1ε



ε
i 
i
Константы K-ε модели турбулентного переноса
C m = 0.09; C e1 = 1.43;
C e2 = 1.92; s k = 1; s e = 1.3

6. Основные уравнения
Уравнение неразрывности
¶r
¶ r vi
+
=0
¶t
¶ xi
r
Уравнение диффузии
dC i
¶
r
=
dt
¶x j
æ nt ¶ C i
çr
ç s ¶x
ç d
è
j
ö
÷ Ri
+
÷
÷
ø
Уравнение теплопереноса
ρ
dT
1 ∂  ν t ∂T
=
ρ
dt
c p ∂x i  σ t ∂x i
Уравнение импульсов
 − E +Q −Q
÷
rad
r

d ui
¶
¶p
=
τt ,ij + r gi
dt
¶x j
¶ xi
Уравнение движения продуктов диссоциации
dC r ,i
r
= R r ,i
dt
Уравнение состояния
p = ρ RT ∑
Уравнение энергии турбулентных пульсаций
i
Сi
µi
Коэффициент турбулентного
переноса
∂v j
dK
∂  ν t ∂K 
=
ρ
+ τ t ,ij
− ρε

÷
dt
∂x i  σ k ∂x i 
∂x i
nt = C mK 2 / e
Уравнение диссипации турбулентных пульсаций
ρ
Константы K-e модели
турбулентного переноса
∂v j
dε
∂  ν t ∂ε  ε 
ρ
=
ρ
+  C 1ετ t ,ij
− C 1ε ρε 
÷
dt
∂x i  σ ε ∂x i ÷ K 
∂x i



C m = 0.09; C e1 = 1.43;
C e2 = 1.92; s k = 1; s e = 1.3

7. Диффузионная схема горения
Интенсивности реакций
C n H m + n2O2 ® n6CO2 + n4H 2O
æ C 2m C 4 m C 6m ö
e
1
1
1÷
R 1 = - A r min çC 1,
,
,
÷
ç nm nm nmø
÷
è
K
2 2
4 4
6 6
A =4
- эмпирическая константа
Баланс масс
R 2 = R 1n2m m
2 1
R 4 = - R 1n4m m
4 1
R 6 = - R 1n6m m
6 1
Баланс тепла
Q = q1R 1
- брутто-реакция
Magnussen B.F., Hjertager B.H. On
the mathematical modelling of
turbulent combustion with special
emphasis on soot formation and
combustion.// Sixteenth Symp. (Int.)
on Combustion, The Combustion
Institute, Pittsburgh, PA, 1976,
pp.711 – 729.

8. Схема горения с учетом кинетики химических реакций
Интенсивности реакций
R1 =
+
R2
m rC1 m rC 2
E
ср
ср
exp - a 1
m
m
RT
1
2
(
rm5 rm2
k
k
E
=
A2 exp - a 2
m m
RT
5
2
(
)
)
R2 = r 2
m3
k
E
A 3 exp - a 3
m
RT
3
(
R r+1 = r
m4 +
k
E
Ar 1 exp - ar 1
m
RT
4
R r- 1 =
r m r 1 - n1
k
A T
m1 r1
r
R r+2 = r
m2 +
k
A
m r2
2
R r- 2 =
)
r m r 2 - n2
k
A T
m2 r2
r
( )
E
exp ( RT )
ar 2
Баланс масс
Баланс тепла
r
R = (R 1, R 2, R 3, R 4 , R 5, 0)
Q = q1R 1 + q5R 5
+
R 2 = - R 1n2m - R 2 m
2
2
Qr = qr 1(R r+1 − R r−1) + qr 2(R r+2 − R r−2 )
+
R 3 = 2R 2 m - 2R 2 m
3
3
R 4 = R 1n4m
4
+
R 5 = R 1n5m - 2R 2 m + 2R 2 m
5
5
5
Смирнов
Н.Н.,
Никитин
В.Ф.
Исследования перехода горения в
детонацию в газах.//
Успехи механики. 2005, т.3, N1, с.3-30.