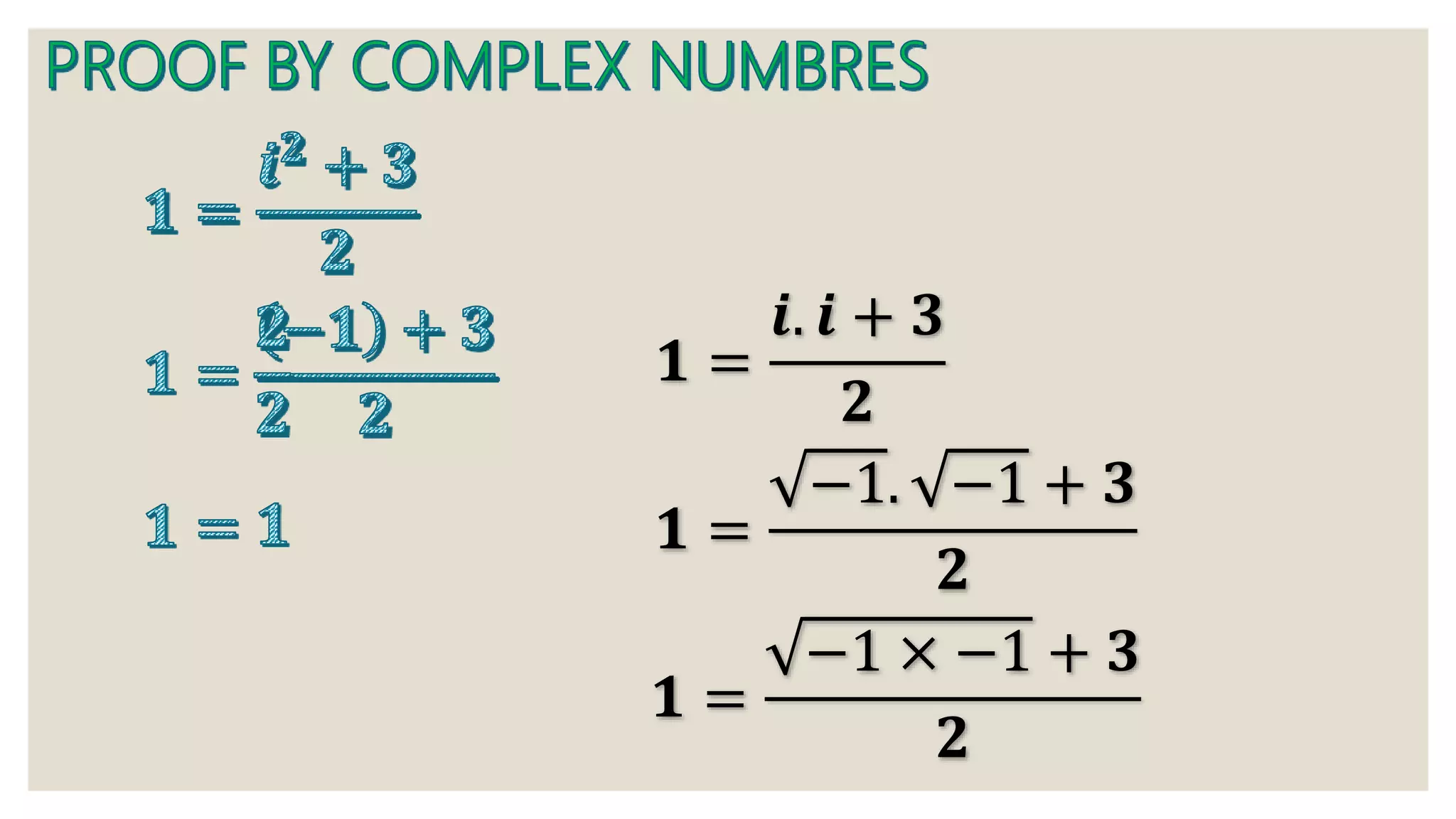The document appears to be a review of mathematics that includes:
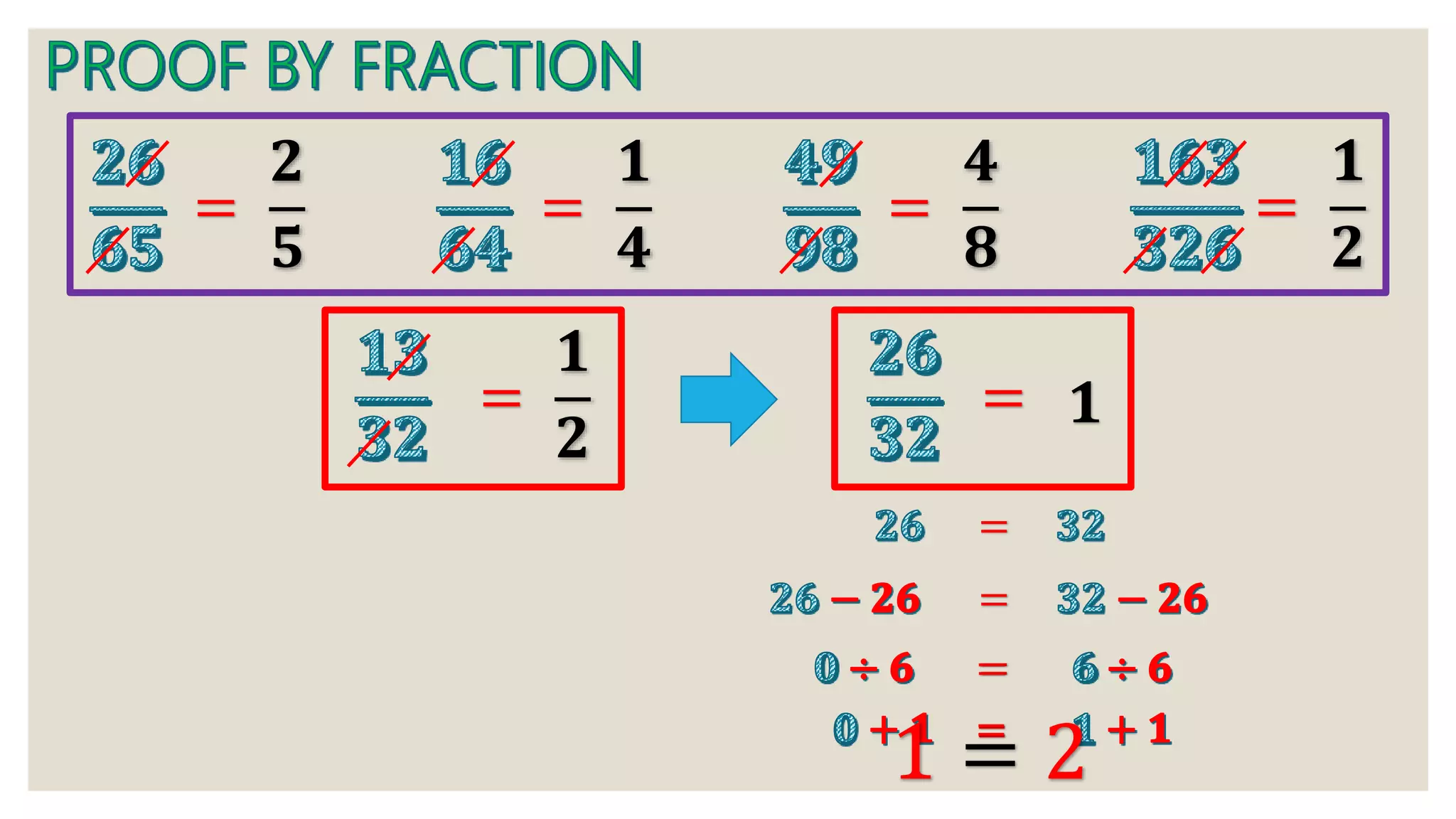
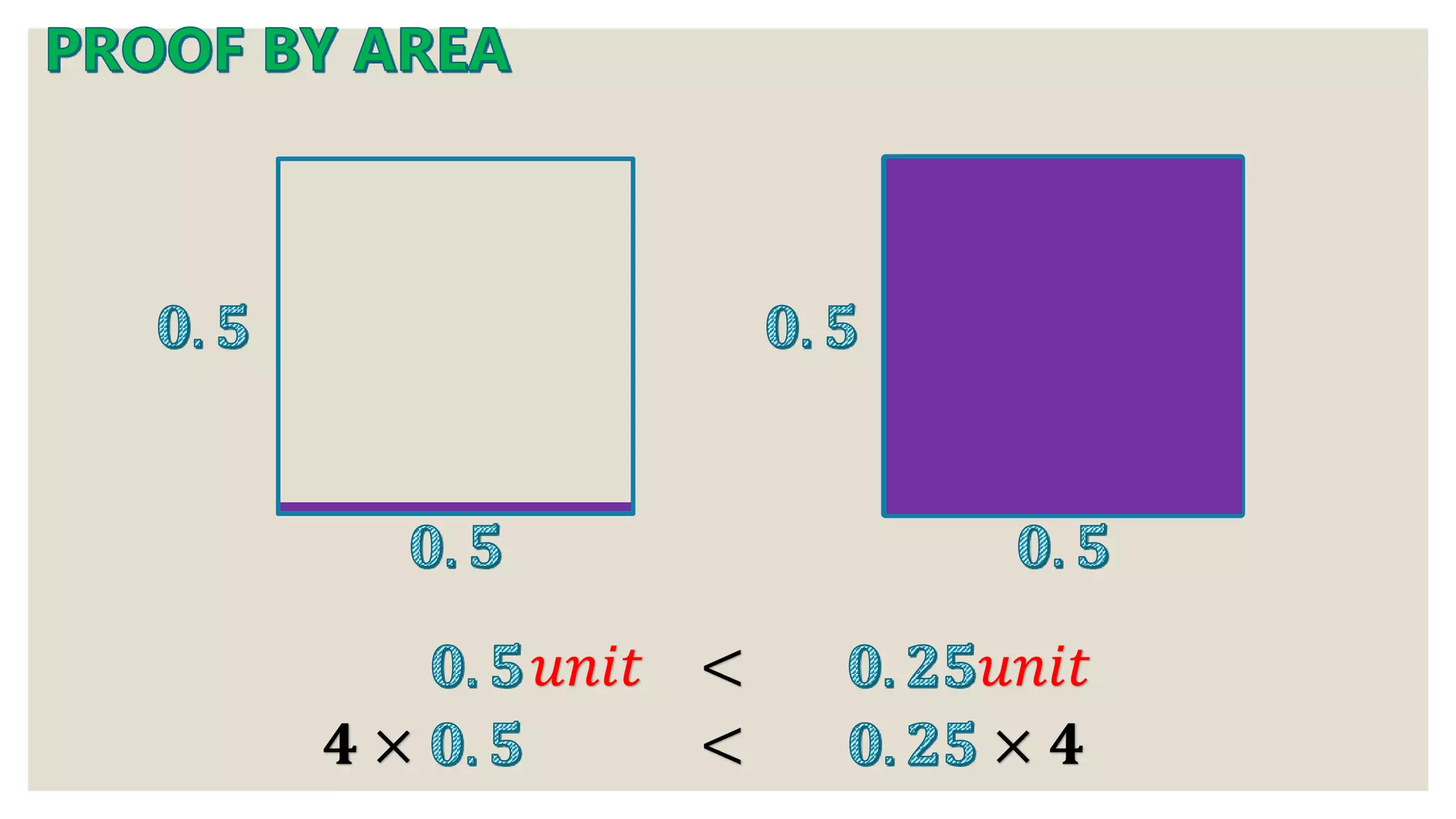
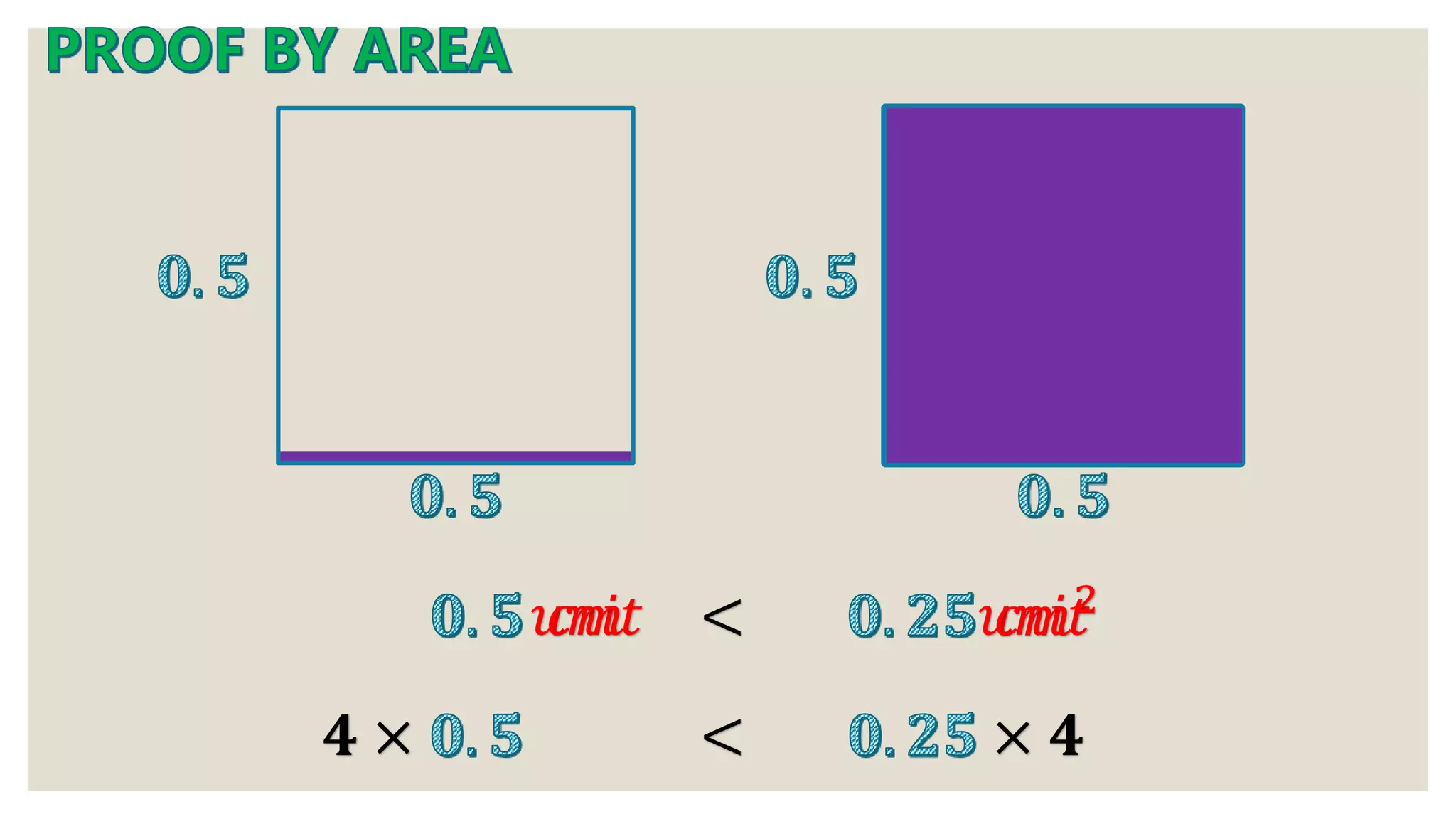
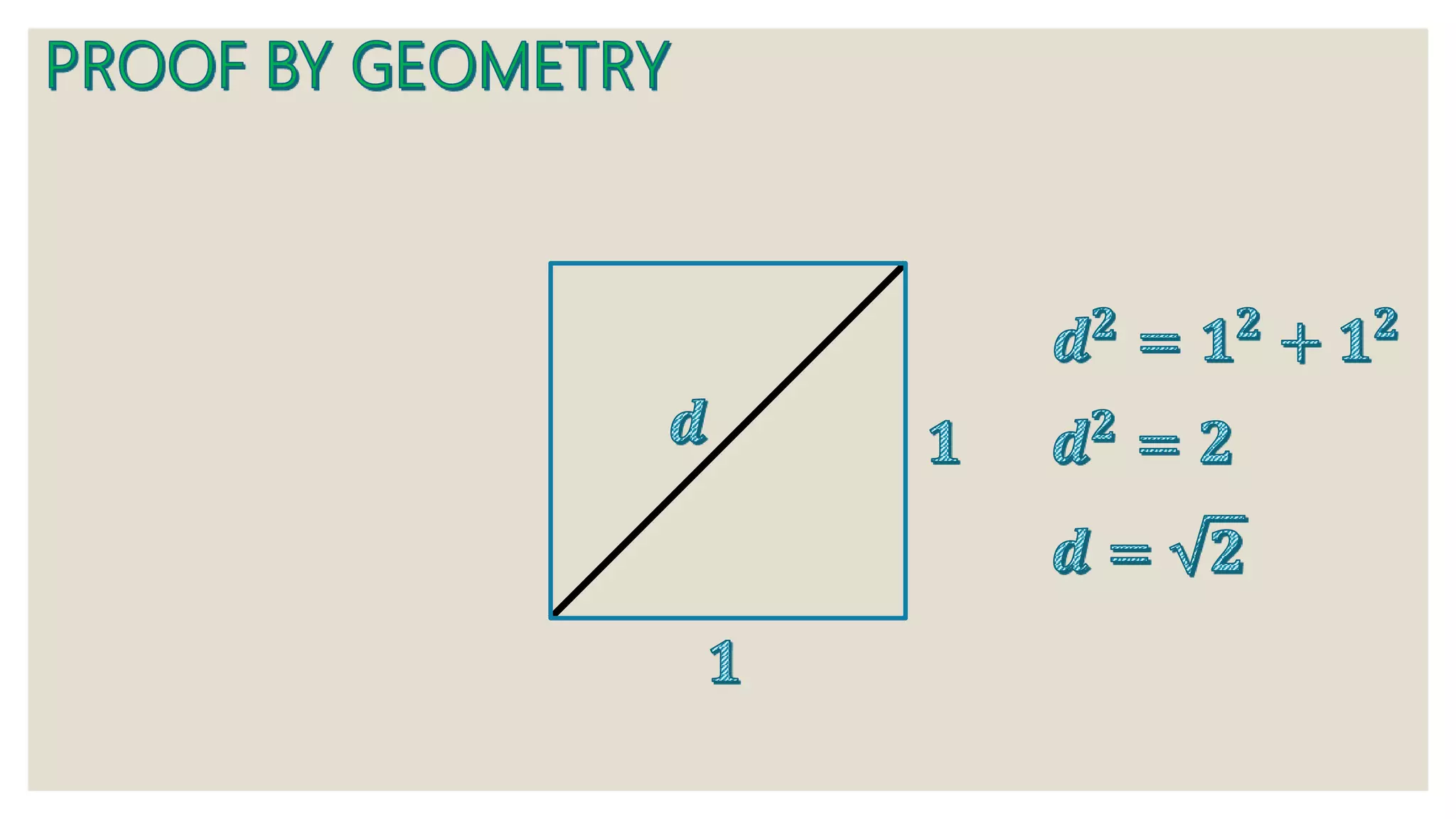
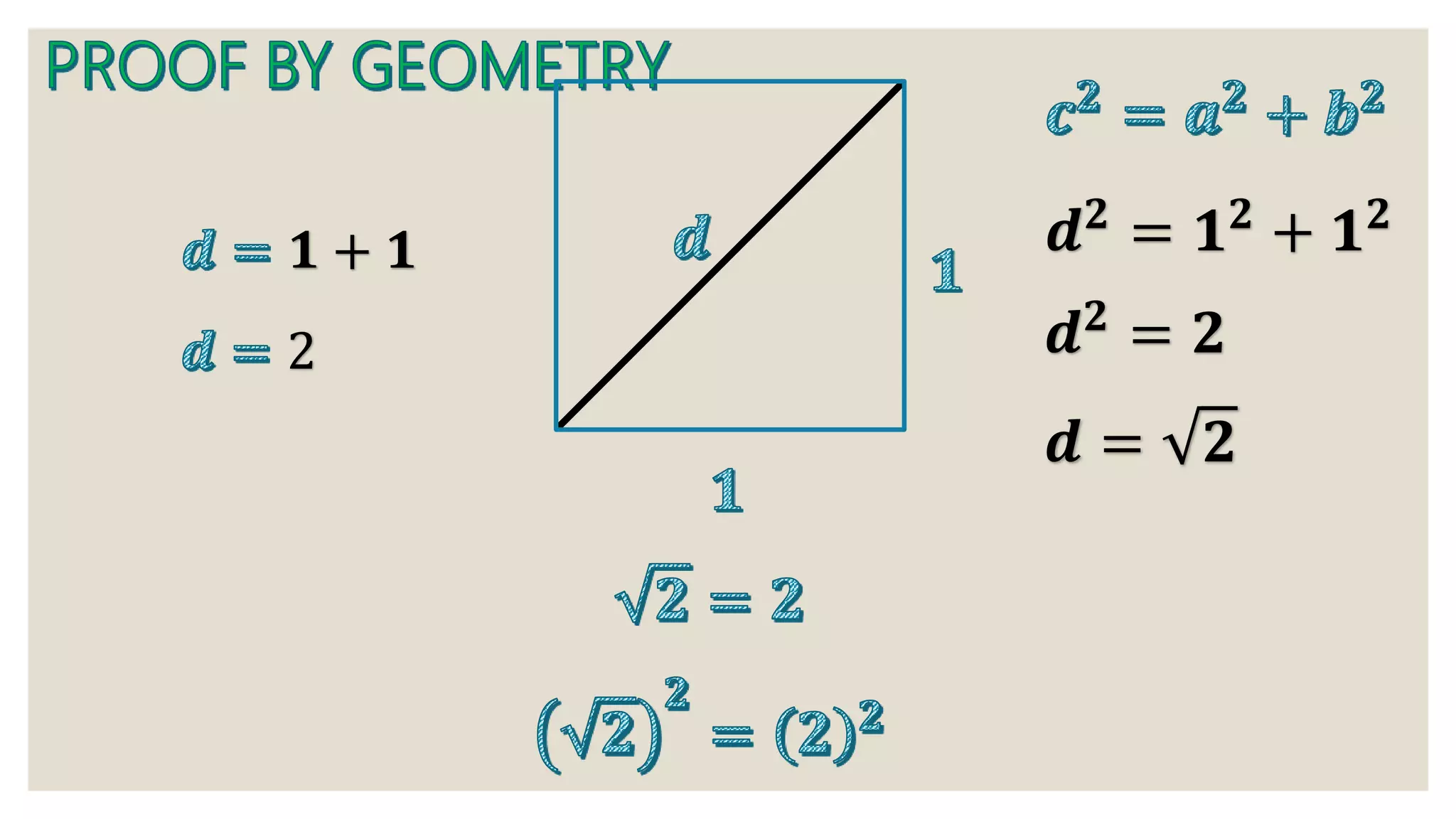
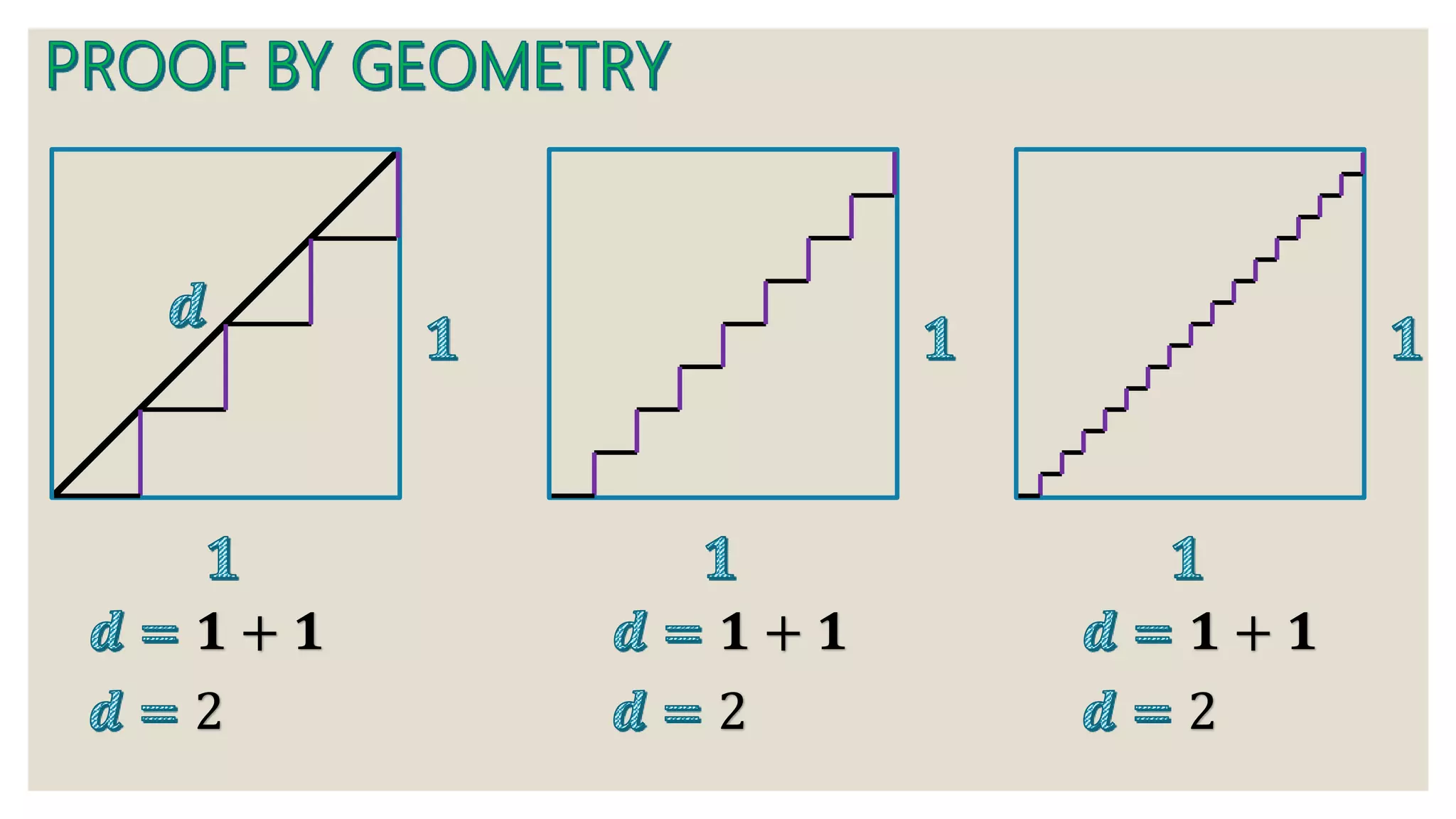
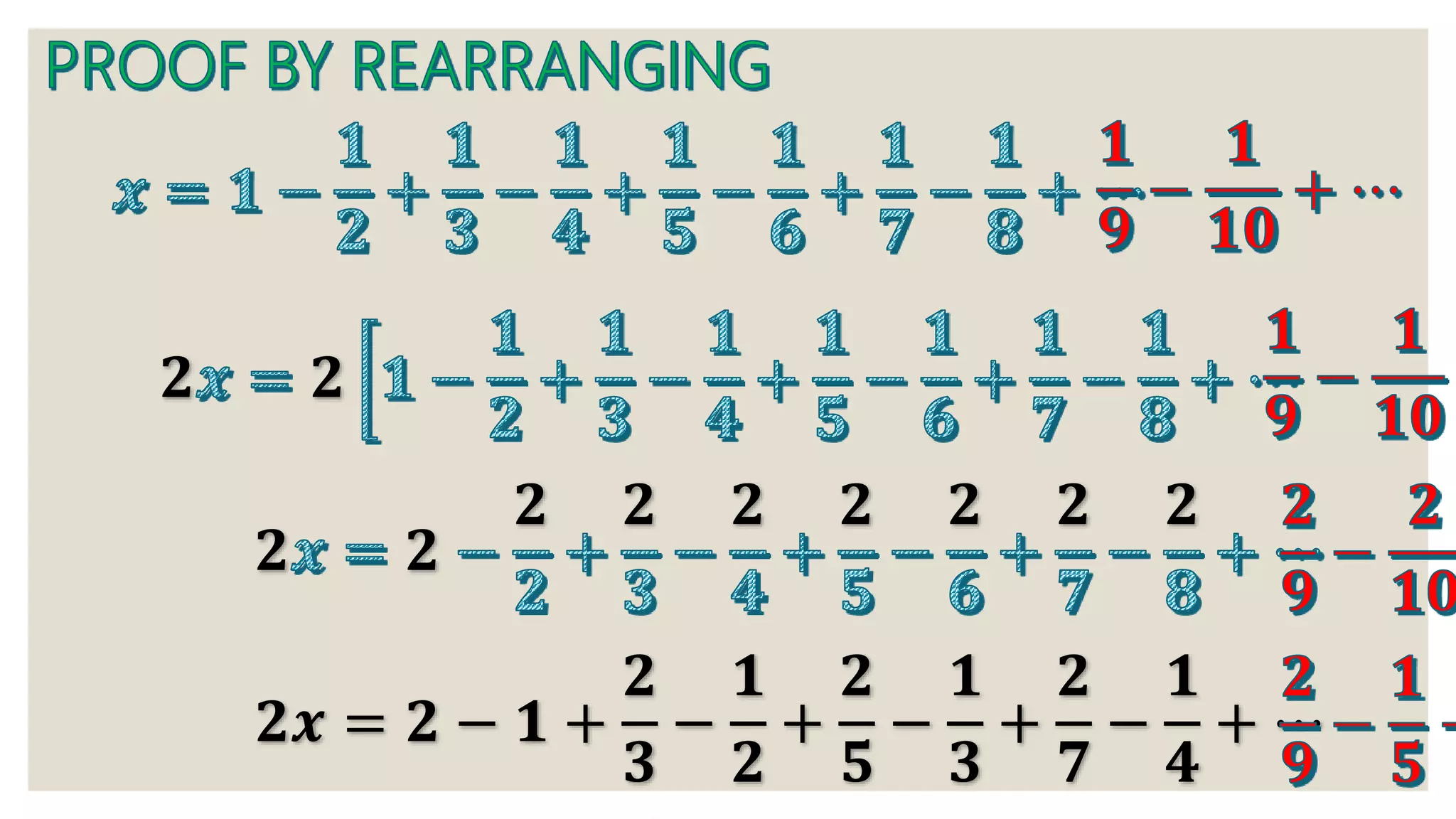
1) A series of mathematical equations and steps working through algebraic expressions and series.
2) Discussion of variables, operations, and mathematical concepts like associative law.
3) Questions posed and answered in a brief, abstract manner.