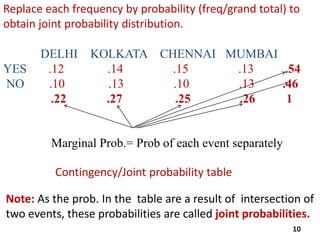
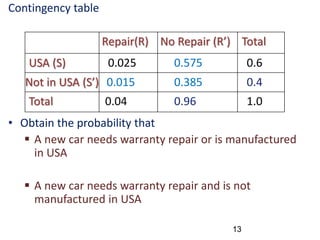
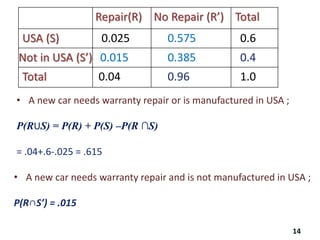
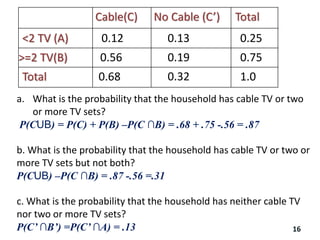
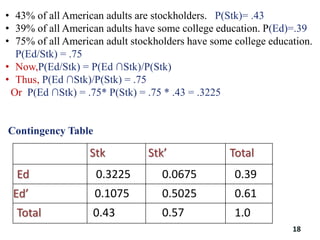
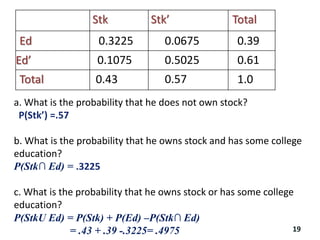
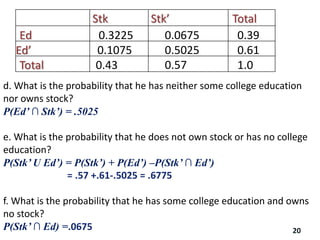
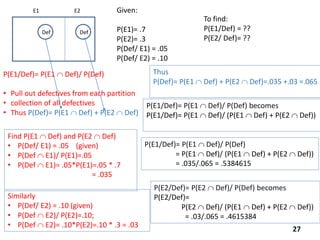
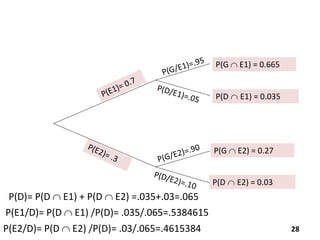
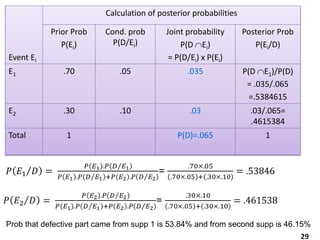
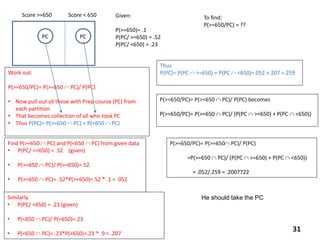
The document reviews essential concepts of probability theory relevant to business applications, including definitions of random experiments, sample spaces, events, and laws of probability. It also presents various exercises demonstrating the calculation of probabilities using joint and marginal distributions, along with real-world examples such as market surveys and demographic studies. Additionally, it introduces Bayes' theorem for calculating posterior probabilities and discusses decision-making regarding preparation courses based on probabilities.

1. Quantitative Applications in Business - I

2. A Review of Probability Theory
2

3. • Random Experiment is an experiment which results in
any one of the possible outcomes. Though repeated
under identical conditions, the result is not unique.
• Sample Space is an exhaustive list of all the possible
outcomes of a random experiment.
• The repetitions of the experiment are known as trials.
• An outcome of a random experiment is called an event.
3

4. • Events are said to be mutually exclusive or disjoint, if
the happening of any one of them rules out the
happening of all the others. No two or more of them
can happen simultaneously (in a single trial). A∩B = φ
i.e. P(A∩B)= 0
• The events are said to be independent, if the happening
of an event does not affect the happening of any other
event. P(A∩B)=P(A).P(B)
• The event ‘A occurs’ and the event ‘A does not occur’
(denoted by Ac or A’) are called complementary events
to each other. P(A)’=1-P(A)
4

5. • In general
 S is a sample space
 A is some event in S. ( )
 nA is the number of occurrences of A (favorable)
 n is the total number of outcomes.
 The Probability of event A is
S
A 
n
n
A
P A

)
(
1)
be
must
S
in
outcomes
all
of
es
probabliti
the
of
(Sum
1
)
(
(ii)
0
)
(
1
(i)
NOTE



S
P
A
P
5

6. • Addition Law of Probability
 P(AUB) = P(A) + P(B) – P(A ∩B)
 P(AUB) = P(A) + P(B), provided A∩B = φ
 A∩B = φ means A and B are mutually exclusive
A B
A ∩B
6

7. • Multiplication Law of probability
 When A and B are independent events, then
P(A∩B)=P(A).P(B) (Joint Probability of A and B)
 When A and B are dependent events, then
P(A∩B) = P(A|B) . P(B) or P(A∩B) = P(B|A) . P(A)
Where Probability of A given that B has already occurred is
called Conditional probability
 P(A|B) = P(A∩B)/ P(B); P(B|A) = P(A∩B)/ P(A)
Note: For independent events P(A|B)=P(A); P(BA)=P(B)
7

8. A market survey was conducted in four cities to find out the
preference for brand ‘A’ soap. The responses are shown
below:
DELHI KOLKATA CHENNAI MUMBAI
YES 45 55 60 50 210
NO 40 50 40 50 180
85 105 100 100 390
A) What is the probability that a consumer selected at
random, preferred brand A?
B) Probability that a consumer preferred brand A and was
from Chennai ?
C) Probability that a consumer preferred brand A given that
he was from Chennai ?
D) Given that a consumer preferred brand A, what is the
probability that he was from Mumbai ?
Sol: A) 210/390 B) 60/390 C) 60/100 D) 50/210 8

9. Joint Probability Distribution
9

10. Replace each frequency by probability (freq/grand total) to
obtain joint probability distribution.
DELHI KOLKATA CHENNAI MUMBAI
YES .12 .14 .15 .13 .54
NO .10 .13 .10 .13 .46
.22 .27 .25 .26 1
Marginal Prob.= Prob of each event separately
Contingency/Joint probability table
Note: As the prob. In the table are a result of intersection of
two events, these probabilities are called joint probabilities.
10

11. DELHI KOLKATA CHENNAI MUMBAI
YES .12 .14 .15 .13 .54
NO .10 .13 .10 .13 .46
.22 .27 .25 .26 1
A) What is the probability that a consumer selected at
random, preferred brand A?
B) Probability that a consumer preferred brand A and was
from Chennai ?
C) Probability that a consumer preferred brand A given that
he was from Chennai ?
D) Given that a consumer preferred brand A, what is the
probability that he was from Mumbai ?
Sol: A) .54 B) .15 C) .6 (.15/.25) D) .24 (.13/.54)
11

12. Exercise:
• Each year, ratings are complied concerning the performance of
new cars during first 90 days of use.
• Cars are categorized according to
 if the car needs warranty related repair
 If the car is manufactured in USA
• Based on the data collected, it was found that
 P(Car needs warranty repair) = 0.04
 P (Car manufactured in USA) = 0.60
 P (needs warranty repair and manufactured in USA) = 0.025
• Make contingency table
• Obtain the probability that
 A new car needs warranty repair or is manufactured in USA
 A new car needs warranty repair and is not manufactured in
USA
12

13. Contingency table
• Obtain the probability that
 A new car needs warranty repair or is manufactured
in USA
 A new car needs warranty repair and is not
manufactured in USA
Repair(R) No Repair (R’) Total
USA (S) 0.025 0.575 0.6
Not in USA (S’) 0.015 0.385 0.4
Total 0.04 0.96 1.0
13

14. • A new car needs warranty repair and is not manufactured in USA ;
P(R∩S’) = .015
• A new car needs warranty repair or is manufactured in USA ;
P(RUS) = P(R) + P(S) –P(R ∩S)
= .04+.6-.025 = .615
Repair(R) No Repair (R’) Total
USA (S) 0.025 0.575 0.6
Not in USA (S’) 0.015 0.385 0.4
Total 0.04 0.96 1.0
14

15. Exercise:
According to Nielsen Media Research, approximately 68% of all
U.S. households with television have cable TV. Seventy-five percent
of all U.S. households with television have two or more TV sets.
Suppose 56% of all U.S. households with television have cable TV
and two or more TV sets. A U.S. household with television is
Randomly selected.
a. What is the probability that the household has cable TV or two
or more TV sets?
b. What is the probability that the household has cable TV or two
or more TV sets but not both?
c. What is the probability that the household has neither cable TV
nor two or more TV sets?
Ans: .87, .31, .13
15

16. Cable(C) No Cable (C’) Total
<2 TV (A) 0.12 0.13 0.25
>=2 TV(B) 0.56 0.19 0.75
Total 0.68 0.32 1.0
a. What is the probability that the household has cable TV or two
or more TV sets?
P(CUB) = P(C) + P(B) –P(C ∩B) = .68 + .75 -.56 = .87
b. What is the probability that the household has cable TV or two or
more TV sets but not both?
P(CUB) –P(C ∩B) = .87 -.56 =.31
c. What is the probability that the household has neither cable TV
nor two or more TV sets?
P(C’ ∩B’) =P(C’ ∩A) = .13 16

17. Exercise: A study for the Nasdaq Stock Market revealed that 43% of all
American adults are stockholders. In addition, the study determined
that 75% of all American adult stockholders have some college
education. Suppose 39% of all American adults have some college
education. An American adult is randomly selected
a. What is the probability that he does not own stock?
b. What is the probability that he owns stock and has some college
education?
c. What is the probability that he owns stock or has some college
education?
d. What is the probability that he has neither some college
education nor owns stock?
e. What is the probability that he does not own stock or has no
college education?
f. What is the probability that he has some college education and
owns no stock?
Ans: a .57; b .3225; c .4975; d .5025; e .6775; f .0675 17

18. Stk Stk’ Total
Ed 0.3225 0.0675 0.39
Ed’ 0.1075 0.5025 0.61
Total 0.43 0.57 1.0
• 43% of all American adults are stockholders. P(Stk)= .43
• 39% of all American adults have some college education. P(Ed)=.39
• 75% of all American adult stockholders have some college education.
P(Ed/Stk) = .75
• Now,P(Ed/Stk) = P(Ed ∩Stk)/P(Stk)
• Thus, P(Ed ∩Stk)/P(Stk) = .75
Or P(Ed ∩Stk) = .75* P(Stk) = .75 * .43 = .3225
Contingency Table
18

19. Stk Stk’ Total
Ed 0.3225 0.0675 0.39
Ed’ 0.1075 0.5025 0.61
Total 0.43 0.57 1.0
a. What is the probability that he does not own stock?
P(Stk’) =.57
b. What is the probability that he owns stock and has some college
education?
P(Stk∩ Ed) = .3225
c. What is the probability that he owns stock or has some college
education?
P(StkU Ed) = P(Stk) + P(Ed) –P(Stk∩ Ed)
= .43 + .39 -.3225= .4975 19

20. d. What is the probability that he has neither some college education
nor owns stock?
P(Ed’ ∩ Stk’) = .5025
e. What is the probability that he does not own stock or has no college
education?
P(Stk’ U Ed’) = P(Stk’) + P(Ed’) –P(Stk’ ∩ Ed’)
= .57 +.61-.5025 = .6775
f. What is the probability that he has some college education and owns
no stock?
P(Stk’ ∩ Ed) =.0675
Stk Stk’ Total
Ed 0.3225 0.0675 0.39
Ed’ 0.1075 0.5025 0.61
Total 0.43 0.57 1.0
20

21. 21
Contingency Table of Gender and Pass
Pass
Did Not
Pass
Total
Men 6 9 15
Women 10 15 25
Total 16 24 40
Example: Gender and Pass Rate
Check whether Gender and Passing are independent.
If gender and passing are independent, then the probability of passing will not
change if a case's gender is known.
P(Pass)=16/40=0.4
P(Pass/Man)=6/15=0.4
Thus, gender and passing are independent

22. Revision of Probabilities: Bayes’ Rule
22

23. 23

24. 24

25. 25

26. 26

27. E1 E2
Def Def
Given:
P(E1)= .7
P(E2)= .3
P(Def/ E1) = .05
P(Def/ E2) = .10
To find:
P(E1/Def) = ??
P(E2/ Def)= ??
P(E1/Def)= P(E1  Def)/ P(Def)
• Pull out defectives from each partition
• collection of all defectives
• Thus P(Def)= P(E1  Def) + P(E2  Def)
P(E1/Def)= P(E1  Def)/ P(Def) becomes
P(E1/Def)= P(E1  Def)/ (P(E1  Def) + P(E2  Def))
Find P(E1  Def) and P(E2  Def)
• P(Def/ E1) = .05 (given)
• P(Def  E1)/ P(E1)=.05
• P(Def  E1)= .05*P(E1)=.05 * .7
= .035
Thus
P(Def)= P(E1  Def) + P(E2  Def)=.035 +.03 =.065
P(E1/Def)= P(E1  Def)/ P(Def)
= P(E1  Def)/ (P(E1  Def) + P(E2  Def))
= .035/.065 = .5384615
P(E2/Def)= P(E2  Def)/ P(Def) becomes
P(E2/Def)=
P(E2  Def)/ (P(E1  Def) + P(E2  Def))
= .03/.065 = .4615384
Similarly
• P(Def/ E2) = .10 (given)
• P(Def  E2)/ P(E2)=.10;
• P(Def  E2)= .10*P(E2)=.10 * .3 = .03
27

28. P(G  E1) = 0.665
P(D  E1) = 0.035
P(G  E2) = 0.27
P(D  E2) = 0.03
P(D)= P(D  E1) + P(D  E2) =.035+.03=.065
P(E1/D)= P(D  E1) /P(D)= .035/.065=.5384615
P(E2/D)= P(D  E2) /P(D)= .03/.065=.4615384 28

29. Event Ei
Calculation of posterior probabilities
Prior Prob
P(Ei)
Cond. prob
P(D/Ei)
Joint probability
P(D Ei)
= P(D/Ei) x P(Ei)
Posterior Prob
P(Ei/D)
E1 .70 .05 .035 P(D E1)/P(D)
= .035/.065
=.5384615
E2 .30 .10 .03 .03/.065=
.4615384
Total 1 P(D)=.065 1
Prob that defective part came from supp 1 is 53.84% and from second supp is 46.15%
29

30. Exercise: The Graduate Management Admission Test (GMAT)
is a requirement for all applicants of MBA programs. A variety
of preparatory courses are designed to help applicants
improve their GMAT Scores, which range from 200 to 800.
Suppose that a survey of MBA students reveals that among
GMAT scorers above 650, 52% took a preparatory course;
whereas among GMAT scorers of less than 650 only 23% took
a preparatory course. An applicant to an MBA program has
determined that his probability of getting that high a score is
quite low i.e. 10%. He is considering taking a preparatory
course that costs $500. He is willing to do so only if his
probability of achieving 650 or more doubles. What should
he do?
30

31. Score >=650 Score < 650
PC PC
Given:
P(>=650)= .1
P(PC/ >=650) = .52
P(PC/ <650) = .23
To find:
P(>=650/PC) = ??
Work out:
P(>=650/PC)= P(>=650  PC)/ P(PC)
• Now pull out all those with Prep course (PC) from
each partition
• That becomes collection of all who took PC
• Thus P(PC)= P(>=650  PC) + P(<650  PC)
P(>=650/PC)= P(>=650  PC)/ P(PC) becomes
P(>=650/PC)= P(>=650  PC)/ (P(PC  >=650) + P(PC  <650))
Find P(>=650  PC) and P(<650  PC) from given data
• P(PC/ >=650) = .52 (given)
• P(>=650  PC)/ P(>=650)=.52
• P(>=650  PC)= .52*P(>=650)=.52 * .1 = .052
Thus
P(PC)= P(PC  >=650) + P(PC  <650)=.052 +.207 =.259
P(>=650/PC)= P(>=650 PC)/ P(PC)
=P(>=650  PC)/ (P(PC  >=650) + P(PC  <650))
= .052/.259 = .2007722
Similarly
• P(PC/ <650) = .23 (given)
• P(<650  PC)/ P(<650)=.23
• P(<650  PC)= .23*P(<650)=.23 * .9 = .207
He should take the PC
31