Downloaded 16 times
![[DL Hacks] Deterministic Variational Inference for RobustBayesian Neural Netw...](https://cdn.slidesharecdn.com/ss_thumbnails/adobepdffile2-190628001736-thumbnail.jpg?width=640&height=640&fit=bounds)
Prml nn
- 1.
- 2. 5.5.0 ニューラルネットワークの正則化 • 最適な隠れユニットの数Mっていうのが存在するはず。 •P.228の図5.1を見て思い出していただければ… • 誤差関数には局所解が多数存在するので、単純な関数 にはならない。 1. 複数のMで学習して結果をグラフにして決める 2. 正則化を追加する 最も単純な荷重減衰と呼ばれるもの。 λの選択に寄って有効なMが変化する
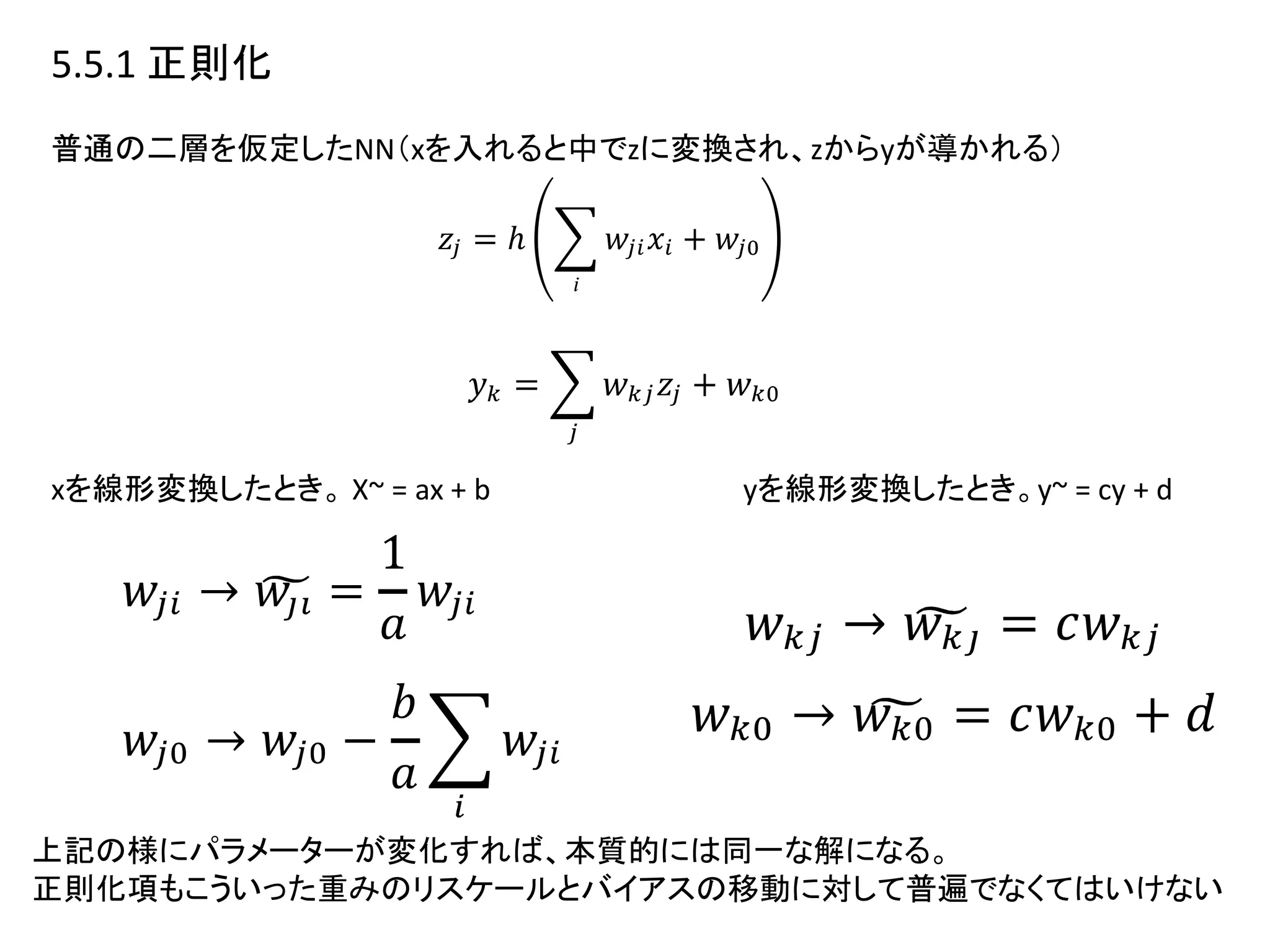
- 3. 5.5.1 正則化 • 単純な物には限界がある •ネットワーク写像のスケーリング性質と矛盾しない状態が欲 しい • データを線形変換した時、線形変換分だけ重みが異なる 等価なネットワークが得られること。 • 正則化はこの性質を持つべき。 • 正則化は入力データが線形変換されても同一の解を持 つべき。 • が、荷重減衰はその性質を持たない。 • スケールアップ分がWTWに入ってしまうから。
- 4. 5.5.1 正則化 普通の二層を仮定したNN（xを入れると中でzに変換され、zからyが導かれる） xを線形変換したとき。 X~= ax + b yを線形変換したとき。y~ = cy + d 上記の様にパラメーターが変化すれば、本質的には同一な解になる。 正則化項もこういった重みのリスケールとバイアスの移動に対して普遍でなくてはいけない
- 5. 5.5.1 正則化 それがこれ。 1層 2層 W^2で生まれる、a^2とc^-2が消える様になっている。 無矛盾な正則化を得る事が出来た。
- 6. 5.5.2 早期終了 ネットワークの複雑さを制御したい for過学習の回避 一般に検証用集合（データ）に対する誤差は反復回数が増える程増加するが、一 定の回数以降は過学習の影響で誤差が増加する。 よって途中で学習を止める事が良い。
- 7. 5.5.3不変性 • パターン認識の多くの応用例では、入力変数がある変換を受けても変化しない 事が求められる。▶︎不変 • 画像内での位置 •サイズ • 十分多くの訓練パターンが利用可能なら、NNは少なくとも近似的には不変性を 得られる。 • 様々な位置に認識したい物体がある画像がある状態 • ただ、訓練例題が限られてたり、位置とサイズが違うという複数の不変性があ る時には実用的ではない。 対応は以下の４つ 1. 訓練パターンをコピー変換して訓練集合を増加させる。（計算量増える） 2. 正則化を利用する。（接線伝搬法） 3. 変換されても不変である様な特徴を抽出する（職人芸） 4. NNの構造の中に不変性を構築する（たたみこみNN）
- 8. 5.5.4 接線伝搬法 • 正則化を使って入力の変換に対する不変性を持たせる。 •入力の変化に対する出力の変化の関数を定義して、それを誤差関数に追加し て最小化させてしまおうというアイデア。 • 学習時に誤差関数と一緒に出力の変化も重み付きだけど小さくなるので、入力 が変わっても出力が変わりにくくなる。 • λは訓練データに対するフィッティングと不変性のバランスを学習する。 • 実装時にはtは差分で近似。 • 変換が複数ならその分正則化が必要。 変換後のX 変換 変換が微増した時のXの変化分 変換が微増した時のyの変化分
- 9. 5.5.6 たたみ込みニューラルネットワーク • NNの構造の中に不変性を構築したい３つの機構 •局所的受容野 • 重み共有 • 部分サンプリング • たたみ込みNNの構造（こんなイメージ。） • 10X10の画素があり、特徴マップのユニットが5×5の１区画のみから入力 を受けているとする。
- 10.
- 11. 5.5.6 たたみ込みニューラルネットワーク • たたみ込みユニットの出力が、ネットワークの部分サンプリング層の入力。 •位置がぼやける。 • 特徴マップの2x2のユニット領域から入力を受ける。 • 受容野を連続で重なりが無い様にすると、部分サンプリング層のユニット配列は行列ともにた たみ込み層の半分のサイズになる • 画素の部分で右に平行移動が発生すると、特徴マップが右にずれるけど、結局部分サンプリ ング層では同じユニットに対して作用する。 たたみ込み層 部分サンプリング層 重みを付けて平均化して、 バイアスつけてシグモイド 関数に突っ込む
- 12. 5.5.6 たたみ込みニューラルネットワーク • 実用的な構造としては、たたみ込み層と部分サンプリング層の組が複数存在す る事もある。（？） •不変性は層を経る毎に強くなる。 • 部分サンプリング層の１つのユニットの平面に対し、それを入力するたたみ込 み層の特徴マップは複数存在する事もある。 • ネットワークの最後の層では、多くの場合、完全結合であり、完全に適応的な 層である。（？） • 局所的受容野を用いるので、重みの数は完全結合の物より少ない。 • 誤差関数の勾配を評価して逆伝搬法を用いれば、誤差最小化で学習が出来る。 • 重み共有の制約を満たす為には多少修正が必要。
- 13. 5.5.7 ソフト重み共有 • 重み共有は一定のグループに属する重みを等しくして不変性を作っていた。 •ただ、制限の形が先にわかっていないとだめ。 • ＝どの位平行移動するってわかっててその制約をつける。 • 正則化の導入に置き換えて、同じグループに属する重みがにた様な値を取り やすいという状態にしてあげる。▶︎ソフト重み共有 • その際グループ分けや、グループの重みの平均や分散をすべて学習過程の一 部として決定してしまう。 荷重減衰正則化項が重みのガウス事前分布の負の対数尤度と見なせる事から、混合 ガウス分布を用いれば複数グループを表現出来る。 混合係数π 負の対数を取るとこうなる。 後は誤差関数に加えて最小化
- 14. 5.5.7 ソフト重み共有 • 最小化の為に微分する。 •混合係数πを事前分布と見なし、事後分布γを導出。 w-μが0に近づく。が、そのその程度は重みiに対する事後 分布γjに比例した大きさになる。 そのグループに属する可能性が高い程0に近づきやすい。 重みと平均の誤差が、事後確率に従って最小化される。 混合係数の合計は1である必要があるので、ソフトマックス関数が用いられる。 正則化誤差関数をnっぽいので偏微分。平均事後分布へと近づく。 w-μがσjに近づく。
- 15. 5.6 混合密度ネットワーク • 分布が多峰性を持つ場合。（逆問題） •あるxを取った時に、yの分布が複数ありそう。
- 16.
- 17. 図5.19の問題を混合密度ネットワークで解いた時のアウトプット • ３つの峰を持った分布になっている。 • それぞれの分布は別々のp(y|x)を持っている。 •aはあるxの値を取った時に３つの分布のどれに属しているか？ の確率を示している。 • bはあるxの値の時のそれぞれの分布で取るyの値を示している。
- 18. 5.7 ベイズニューラルネットワーク • ベイズの枠組みでは予測を行うのにパラメーターの分布について周辺化 をする必要があり、そこがNNでは面倒。 •ネットワーク関数がパラメーターに極度に非線形で依存している。 • 事後分布の対数は非凸で、誤差関数には複数の局所解がある。 • この辺を解決する為にラプラス近似を用いる。 • 事後分布を、そのモードを中心とするガウス分布で近似する。 • さらに、このガウス分布の分散は十分に小さく、事後確率が大きな値 を取るパラメーター空間の領域ではネットワーク関数はパラメータに 関して近似的に線形であると仮定する。 • 上記を行うと、線形回帰モデルと線形クラス分類に類似したモデルが得ら れ、超パラメーターの点推定と、他のモデルとの比較を行う事が出来る。
- 19. 5.7.1 パラメーターの事後分布 平均=NNの関数 分散 重みWの事前分布をガウス分布の形においてしまう。 tの集合Dとした尤度関数 事後分布 •yがwに非線形で依存しているので、事後分布はガウス分布にならない • ラプラス近似を用いて事後分布をガウス分布で近似する。 条件付き確率
- 20.
- 21.
- 22.
- 23.