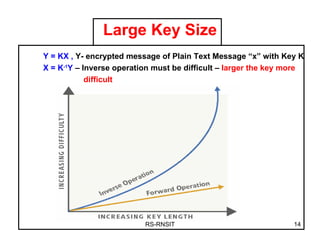
The document provides an overview of elliptic curve cryptography including: 1. It discusses the evolution of cryptography from ancient times to modern algorithms like RSA, AES, and Diffie-Hellman key exchange. 2. It introduces elliptic curve cryptography as an alternative that provides the same level of security with smaller key sizes due to the difficulty of solving the elliptic curve discrete logarithm problem. 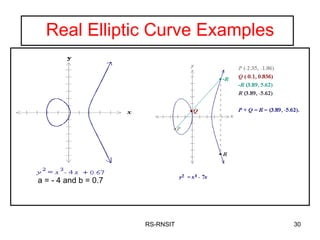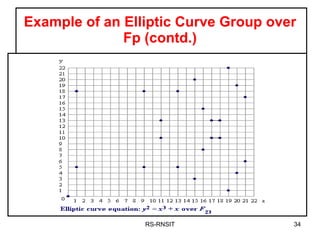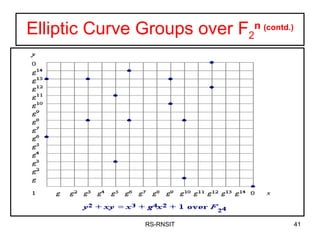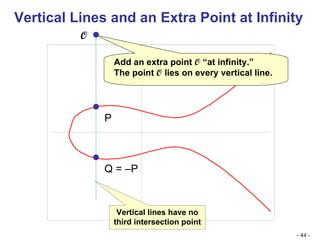3. It provides examples of elliptic curve groups over prime fields and binary fields, showing how points on the curve satisfy the elliptic curve equation over a finite field.

1. Mathematics Towards Elliptic Curve Cryptography by Dr. R. Srinivasan Dean R & D and Post Graduate Studies RNS Institute of Technology, Bangalore Comp Sc. Dept, Mysore 10.9..2011

2. Cryptography Definitions 1 . Cryptography (or cryptology ; from Greek κρυπτός, kryptos , "hidden, secret "; and γράφειν , graphein , "writing", or -λογία , -logia , "study", respectively) [1] is the practice and study of hiding information . Modern cryptography intersects the disciplines of mathematics, computer science , and electrical engineering . 2 . Cryptography is the science of information security . The word is derived from the Greek kryptos , meaning hidden. Cryptography is closely related to the disciplines of cryptology and cryptanalysis 3. Discipline or techniques employed in protecting integrity or secrecy of electronic messages by converting them into unreadable (cipher text) form. Only the use of a secret key can convert the cipher text back into human readable (clear text) form. Cryptography software and/or hardware devices use mathematical formulas (algorithms) to change text from one form to another. Source: Internet

3. Evolution of Cryptography The origin of cryptography is usually dated from about 2000 BC , with the Egyptian practice of hieroglyphics . These consisted of complex pictograms , the full meaning of which was only known to an elite few . The earliest known use of cryptography is found in non-standard hieroglyphs carved into monuments from the Old Kingdom of Egypt circa 1900 BC . Some clay tablets from Mesopotamia somewhat later are clearly meant to protect information — one dated near 1500 BC was found to encrypt a craftsman's recipe for pottery glaze , presumably commercially valuable. Hebrew scholars made use of simple monoalphabetic substitution ciphers such as the Atbash cipher beginning perhaps around 500 to 600 BC Then Romans, Julius Caesar (110BC to 44BC ),….. It was probably religiously motivated textual analysis of the Qur’an which led to the invention of the frequency analysis technique for breaking monoalphabetic substitution ciphers, possibly by Al-Kindi , an Arab mathematician sometime around AD 800

4. Hieroglyphs Hieroglyphs showing the words for Father, Mother, Son, Egyptian Hieroglyphs for Kids ! Source: Internet

5. Zimmermann’s Telegram – January 16, 1917 The message came as a coded telegram dispatched by the Foreign Secretary of the German Empire, ARTHUR ZIMMERMANN, on January 16, 1917, to the German ambassador in Washington D.C., Johann von Bernstorff, at the height ofWorld War I. On January 19, Bernstorff, per Zimmermann's request, forwarded the telegram to the German ambassador in Mexico, Heinrich von Eckardt. Source: Internet

6. Source: Internet

7. Hopes and Assumptions Modern cryptographic algorithms – computational hardness assumptions - hoping such algorithms are hard to break by a HACKER - but only computationally secure !! Information theoretically secure algorithms – probably cannot be broken – like one time pad algorithm - but more difficult to implement compared to the former one But if you do something good , there are others to use it for criminal and bad purposes – Our example : Internet – it was not built with security in mind – leads to hacking – hence we go to cryptography

8. Examples – bad and terrifying Sony’s Play Station & Entertainment Networks : Repeatedly attacked - More than 100 million user’s accounts compromised and the on-line gaming halted for several weeks!! 2. Internet marketing co.: Millions of customer’s e-mail addresses taken from 100 major corporations 3. South Korea’s agricultural co-operative: banking systems crashed for a week – kept 30 million customers from accessing their accounts 4 . Hundai Capital: balckmailers broke into the financial systems – accessed personal details of 1.75 million customers and demanded US $460 000 – not to make the information public 5. Targetted attacks on security vendors also : a hacker fooled with SSL certificates to large websites like Google, Yahoo, Mozilla, and Skype 6. Cyber intrusions : government computer systems in Australia, Canada, France and United States British Government: saw more than 650 attempted intrusions per day !! US Government : received 15,000 hits per day – about one every 6 seconds!! Source: IEEE Spectrum - July 2011

9. Case Study – an intelligent Hacker A stranger on the US Army Computer: few months after the world trade centre attacks: “ I am Solo. Your computer security system is crap . I will continue and disrupt at the highest levels”. Solo scanned thousands of US government machines and discovered glaring security flaws From Feb 2001 to March 2002 : Solo broke into hundreds of PC’s in the Army, Navy Air Force, NASA and US Department of Defense Surfed several months – copied files and passwords He brought down the US Army’s entire Washington D. C. networks – took about 2000 computers for three days He installed a software, “remote anywhere” in all machines and succeeded Alas!! Same software was discovered by Johnson Space Centre – place of purchase was traced and Solo was at last caught Solo’s real name is McKinnon from UK – is he intelligent ?? source: IEEE Spectrum July 2011, pp 27 - 31

10. Cryptography RS-RNSIT Two Categories : Using Private Key (secret key) Public Key – Each user has one pair of Public Key & Private Key - both are good and being used - but strength of Public Key Cryptography is better

11. RS-RNSIT Whitfield Diffie Martin Hellman Pioneers of Public – Key Cryptography

12. The Algorithms RS-RNSIT DES, RSA, AES, Diffie Hellman Key Exchange - but they were proved to be vulnerable for hacker’s attack - in each case the strength is proved to be very good when the Encryption/Decryption Keys are long. * With advances in technology, processors of higher and higher speed are brought out frequently * So hackers are able to identify the key or break the code with little effort.

13. Three Important Points to Note Security and practicality of a given cryptosystem: - depends upon the difference in difficulty between doing a given operation and its inverse. y= f(x) x = f -1 (y) 2. Because amount of efforts (difficulty) depends on functions of key length With longer key lengths – even legitimate forward operations get harder, and require greater resources (chip space and/or processor time), though by a lesser degree than do the inverse operations.

14. Large Key Size RS-RNSIT Y = KX , Y- encrypted message of Plain Text Message “x” with Key K X = K -1 Y – Inverse operation must be difficult – larger the key more difficult

15. One-Way Functions Two basic classes of one-way functions Mathematical Multiplication: Z=X•Y Modular Exponentiation: Z = Y X mod N October 1, 2011 Practical Aspects of Modern Cryptography

16. The Fundamental Equation Z =Y X mod N When Z is unknown, it can be efficiently computed. October 1, 2011 Practical Aspects of Modern Cryptography

17. The Fundamental Equation Z=Y X mod N When X is unknown, the problem is known as the discrete logarithm and is generally believed to be hard to solve. October 1, 2011 Practical Aspects of Modern Cryptography

18. The Fundamental Equation Z= Y X mod N When Y is unknown, the problem is known as discrete root finding and is generally believed to be hard to solve... October 1, 2011 Practical Aspects of Modern Cryptography

19. Diffie-Hellman Key Exchange Alice Randomly select a large integer a and send A = Y a mod N. Compute the key K = B a mod N. Bob Randomly select a large integer b and send B = Y b mod N. Compute the key K = A b mod N. October 1, 2011 Practical Aspects of Modern Cryptography B a = Y ba = Y ab = A b

20. Diffie-Hellman Key Exchange What does Eve, the hacker, see? Y, Y a , Y b … but the exchanged key is Y ab . Belief: Given Y, Y a , Y b it is difficult to compute Y ab . Contrast with discrete logarithm assumption: Given Y, Y a it is difficult to compute a . October 1, 2011 Practical Aspects of Modern Cryptography

21. Three Mathematical Problems The Three Secure Problems: Integer Factorization Problem – RSA algorithm – n = pq (p, q are prime nos.) Finite Field Discrete Logarithm Problem Primitive Root of a Prime No, “p”: If “a” is a primitive root of “p”, then the nos.: a modp, a 2 modp, a 3 modp,….a (n-1) mod p are distinct and consist of integers 1 through p-1 example: 2 is a primitive root of 11 Discrete Logarithm: for any integer “b” and a primitive root “ a” of prime no. p, b  a i mod p where 0  i  (p – 1) “ i” – discrete logarithm of “b” for the base a mod p - represented as dlog a,p Being Used in: Diffie-Hellman Key Exchange, ElGamal encryption RS-RNSIT

22. Three Mathematical Problems(contd.) 3. Elliptic Curve Discrete Logarithm Problem: (ECDL) To form a cryptographic system using elliptic curves we need to find a “hard problem”: Say Q = kP where Q, P  Ep(a,b) and k < p It is relatively easy to calculate Q given k and P but is relatively hard to determine k given Q and P * This is called Discrete Logarithm Problem for Elliptic Curves (DLPEC) RS-RNSIT

23. Problems with RSA & DH Majority of public-key crypto use either integer or polynomial arithmetic with very large numbers/polynomials Imposes a significant load in storing and processing keys and messages So the solution is “ Go to Elliptic Curve Cryptography” - abbreviated as “ECC” * ECC was introduced by Victor Miller and Neal Koblitz in 1985 . RS-RNSIT

24. Using Elliptic Curves In Cryptography The central part of any cryptosystem involving elliptic curves is the elliptic group . All public-key cryptosystems have some underlying mathematical operation. RSA has exponentiation (raising the message or ciphertext to the public or private values) ECC has point multiplication (repeated addition of two points). RS-RNSIT

25. Diffie-Hellman Vs ECC Diffie-Hellman : Key exchange – multiplying pairs of non-zero integers modulo a prime no. “p” Keys generated by exponentiation over the group. Exponentiation defined by repeated multiplication Ex.: a k mod p = (a x ax a x….x a) mod p ECC: Operation over elliptic curves , by addition Multiplication through repeated addition Ex.: a x k = (a+a+a+………+a), k times over the EC Crypt analysis involves determining k given a and (a x k) RS-RNSIT

26. Evolution of Elliptic curves- Cubic Equations RS-RNSIT This is an equation of the form: ay 3 + by 3 + cx 2 y + dxy 2 + exy + fx + gy + h = 0 with rational coefficients Weirstraus has shown that using appropriate transformations changing the coefficients, it becomes Weirstrauss normal form as shown on next slide y 2 = x 3 + ax 2 +bx + c Assuming that roots are all distinct, it is called an Elliptic curve * A simple form: y 2 = x 3 + ax + b

27. If p≠2 Weierstrass equation can be simplified by transformation to get the equation for some constants d,e,f and if p≠3 by transformation to get equation ELIPTIC CURVES - GENERALITY An elliptic curve over where p is a prime is the set of points (x,y) satisfying so-called Weierstrass equation for some constants u,v,a,b,c together with a single element 0 , called the point of infinity.

28. Typical Elliptic Curves ECC- Variables and coefficients of the curves are restricted to elements of a finite field Two families of curves: -------- GF(p) Prime curves over Zp – uses cubic equation. p – a prime number - variables and coefficients – take values in the set of integers from 0 through p-1 - calculations are performed “modulo p” Binary curve – Defined over GF(2 m ) - variables and coefficients –take values in GF(2 m ) - calculations are performed over GF(2 m ) RS-RNSIT

29. Prime Elliptic Curves Please Note: Elliptic Curves are not ellipses!! An elliptic curve - an equation in two variables x & y, with coefficients : y 2 = x 3 + ax + b -- Eqn (1) – a Cubic curve where x,y,a,b are all real numbers So to plot this: y = SQRT (x 3 + ax + b ) For each X and f or given values of a and b, y has both positive and negative values - Set of points E(a,b) consisting of all points (x,y) that satisfy Eqn. (1) together - Different values of (a,b) – different set E(a,b) RS-RNSIT

30. Real Elliptic Curve Examples RS-RNSIT a = - 4 and b = 0.7

31. Three Mathematical Problems (contd) Example: (from Certicom): www.certicom.com Consider the equation: Under the group: E 23 (9,17 ) y 2 mod 23 = (x 3 + 9x+ 17)mod23 What is the discrete logarithm k of Q = (4,5 ) to the base P = (16,5), where Q =kP? Brute force Method : Compute multiples of P until Q is found P = (16,5), 2P = (20,20),……… 9 P=(4,5) = Q Therefore Discrete Logarithm k = 9 Practical Case: K would be too large to be found RS-RNSIT

32. Example of an Elliptic Curve Group over Fp y 2 = x 3 + ax + b Example: An elliptic curve over the field F 23 . With a = 1 and b = 0, the elliptic curve equation is: y 2 = x 3 + x. The point (9,5) satisfies this equation since: y 2 mod p = (x 3 + x)mod p 25 mod 23 = 729 + 9 mod 23 25 mod 23 = 738 mod 23 2 = 2 RS-RNSIT

33. Example of an Elliptic Curve Group over Fp (contd.) The 23 points which satisfy this equation are: (0,0) (1,5) (1,18) (9,5) (9,18) (11,10) (11,13) (13,5) (13,18) (15,3) (15,20) (16,8) (16,15) (17,10) (17,13) (18,10) (18,13) (19,1) (19,22) (20,4) (20,19) (21,6) (21,17) These points may be graphed as shown on next slide RS-RNSIT

34. Example of an Elliptic Curve Group over Fp (contd.) RS-RNSIT

35. Elliptic Curve Groups over F 2 n (contd.) Elements of the field F 2 n are m-bit strings . An elliptic curve with the underlying field F 2 n is formed by choosing the elements a and b within F 2 n (the only condition is that b is not 0). The elliptic curve equation is slightly adjusted for binary representation: y 2 + xy = x 3 + ax 2 + b An elliptic curve group over F 2 n consists of the points on the corresponding elliptic curve, together with a point at infinity, O. There are finitely many points on such an elliptic curve. RS-RNSIT

36. Finite fields of the form GF 2 n (contd.) Computational considerations: A polynomial f(x) in GF(2 n ) is; f(X) = a n-1 x n-I + a n-2 x n-2 + ….a 1 x + a 0 Uniquely represented by its ‘n’ coefficients (a n-1 , a n-2 , ………a 0 ). a i  {0,1} Thus every polynomial in GF(2 n ) can be represented by an n-bit number the coefficients and variables are in finite field Addition: { a n-1 x n-I + a n-2 x n-2 + ….a 1 x + a 0 } +{b n-1 x n-I + b n-2 x n-2 + ….b 1 x + b 0 } = r n-1 x n-I + r n-2 x n-2 + ….r 1 x + r 0 with ri  [ai + bi] mod 2 RS-RNSIT

37. Finite fields of the form GF 2 n (contd.) RS-RNSIT n  {113, 131, 163, 193, 233, 239, 283, 409, 571} Ref: Secg-talk@lists.certicom.com Field Reduction Polynomials F 2 113 f(x) = x 113 + x 9 + 1 F 2 131 f(x) = x 131 + x 8 + x 3 + x 2 + 1 F 2 163 f(x) = x 163 + x 7 + x 6 + x 3 +1 F 2 193 f(x) = x 193 + x 15 + 1 F 2 233 f(x) = x 233 + x 74 + 1 F 2 239 f(x) = x 239 + x 36 + 1 F 2 283 f(x) = x 283 + x 12 + x 7 + x 5 +1 F 2 409 f(x) = x 409 + x 87 + 1

38. Elliptic Curve Groups over F 2 n RS-RNSIT Elements of the field F 2 n are n-bit strings. The rules for arithmetic in F 2 n - defined by polynomial representation Example : Field F 2 4 f(x) = x 4 + x + 1 ; generator g must satisfy the eqn. f(g) = g 4 + g + 1 = 0; i.e: g 4 = g+1 The element g = (0010) is a generator for the field . The powers of g are shown in next slide In a true cryptographic application , the parameter n must be large enough to preclude the efficient generation of such a table otherwise the cryptosystem can be broken. In today's practice, n = 160 is a suitable choice.

39. Elliptic Curve Groups over F 2 n (contd.) RS-RNSIT Ex. g 5 = (g 4 )(g) = (g+1)g = g 2 + g = 0110 g 6 = g 4 .g 2 = (g+1)g 2 = g 3 +g 2 = 1100 g0 = 0001 g4 = 0011 g8 = 0101 g12 = 1111 g1 = 0010 g5 = 0110 g9 = 1010 g13 = 1101 g2 = 0100 g6 = 1100 g10 = 0111 g14 = 1001 g3 = 1000 g7 = 1011 g11 = 1110 g15 = 0001

40. Elliptic Curve Groups over F 2 n (contd.) Going back to the Elliptic curve: y 2 + xy = x 3 + ax 2 + b, setting a= g 4 & b = 1 - one point that satisfies this equation is: ( g5 , g3 ): (g 3 ) 2 + (g 5 )(g 3 ) = (g 5 ) 3 + ( g 4 )( g 5 ) 2 + 1 g 6 + g 8 = g 15 + g 14 + 1 , from the tables on the previous slide, 1100 + 0101 = 0001 + 1001 + 0001 1001 = 1001 Other points that satisfy this equation are shown on next slide RS-RNSIT

41. Elliptic Curve Groups over F 2 n (contd.) RS-RNSIT

42. Adding Points P + Q on E - - P Q P+Q R

43. Doubling a Point P on E - - P 2*P R Tangent Line to E at P

44. Vertical Lines and an Extra Point at Infinity Add an extra point O “at infinity.” The point O lies on every vertical line. - - Vertical lines have no third intersection point Q O P Q = –P

45. Properties of “Addition” on E Theorem: The addition law on E has the following properties : P + O = O + P = P for all P  E. P + (–P) = O for all P  E. (P + Q) + R = P + (Q + R) for all P,Q,R  E. P + Q = Q + P for all P,Q  E. In other words, the addition law + makes the points of E into a commutative group . All of the group properties are trivial to check except for the associative law (c). The associative law can be verified by a lengthy computation using explicit formulas, or by using more advanced algebraic or analytic methods. - -

46. A Numerical Example Using the tangent line construction, we find that 2P = P + P = (-7/4, -27/8). Using the secant line construction, we find that 3P = P + P + P = (553/121, -11950/1331) Similarly, 4P = (45313/11664, 8655103/1259712). As you can see, the coordinates become complicated. - - E : Y 2 = X 3 – 5X + 8 The point P = (1,2) is on the curve E.

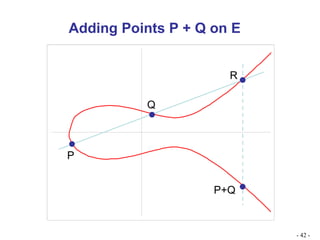
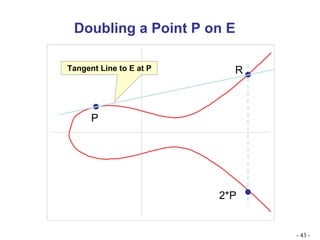
47. Algebraic Description of Addition Calculation of Addition over elliptic curves: For two distinct points P = (x p , y p ) and Q = (x Q , y Q ) not negative to each other, Slope of the line ‘l’ that joins them is :  = (y Q – y P )/ (x Q – x p ) We can express R = P + Q as follows: x R =  2 – x p – x Q ------------- Eqn1 y R = - y p +  (x p – x R ) ----Eqn 2 To add a point to itself, P + P = 2P = R, when y p  0, the expressions are: x R = {[3x 2 p + a]/2y p } 2 – 2 x p y R = {[ 3x 2 p + a]/ 2y p } (x p – x R ) - y p

48. Algebraic Description of Addition (contd.) Actually:  = (y Q – y P )/ (x Q – x p ) mod p if P  Q and  = {[3x 2 p + a]/2y p } mod p if P = Q Example: P = (3, 10) and Q = (9,7) in E 23 (1,1) in y 2 = x 3 + x + 1  = (7-10/9-3)mod 23 = 11 x R = (11 2 -3-9)mod23 = 17 y R = [11(3-17)-10]mod23 =20 So (P+Q) = (17,20) To find 2P = P + P:  = [{3(3 2 ) + 1}/2x10] mod23 = (1/4)mod23 Multiplicative inverse of 4 under Z 23 ,  = (1/4)mid23 = 6 [to check(6x4)mod23 = 1] with xP= xQ = 3 and yP = 10 and substituting in Eqns 1 and 2 on last slide: x R = (6 2 – 3 - 3)mod23 = 30mod23 = 7 y R = {6(3-7) – 10} mod23 = (-34) mod 23 = 12 the point corresponding to 2P = (7, 12)

49. ECC Diffie-Hellman Can do key exchange analogous to D-H users select a suitable curve E p (a,b) select base point G =(x 1 ,y 1 ) with large order n s.t . nG=O “ order, n“ of a point G on an elliptic curve is the smallest +ve integer such that nG = O A & B select private keys n A <n, n B <n compute public keys : P A =n A ×G, P B =n B ×G compute shared key : K =n A × P B , K =n B × P A same since K =n A × n B ×G RS-RNSIT

50. ECC Encryption/Decryption Key Exchange between User A & B must first encode any message M as a point on the elliptic curve P m select suitable curve & point G as in D-H A chooses private key n A <n and computes public key P A =n A ×G to encrypt P m to B : C m ={kG, P m +kP B } , k random positive integer chosen by A decrypt C m : B computes: P m + k P B – n B ( kG ) = P m + k ( n B G )– n B ( kG ) = P m RS-RNSIT

51. Mapping Messages into Points of Elliptic Curves Problem and basic idea The problem of assigning messages to points on an elliptic curve is difficult because there are no polynomial-time algorithms to write down points of an arbitrary elliptic curve. Fortunately, there is a fast randomized algorithm, to assign points of any elliptic curve to messages, that can fail with probability that can be made arbitrarily small. Basic idea: Given an elliptic curve E ( mod p) , the problem is that not to every x there is an y such that (x,y) is a point of E . Given a message (number) m we therefore adjoin to m few bits at the end of m and adjust them until we get a number x such that x 3 + ax + b is a square mod p .

52. Mapping Messages into Points of Elliptic Curves (2) Let K be a large integer such that a failure rate of 1/2 K is acceptable when trying to encode a message by a point. For j from 0 to K verify whether for x = mK + j , x 3 + ax + b ( mod p) is a square ( mod p) of an integer y . If such an j is found, encoding is done; if not the algorithm fails (with probability 1/2 K because x 3 + ax + b is a square approximately half of the time). In order to recover the message m from the point (x,y), we compute:

53. RS-RNSIT Elliptic Curve Digital Signature Algorithm (ECDSA) Proposed by Abdalla , Bellare and Rogaway in 1999. Entity A has domain parameters D = (q, a, b, G, n, h) and public key Q A and private key d A . And entity B has authentic copies of D and Q A . To sign a message m, A does the following: Select a random integer k from [1,n-1]. Compute kG = (x 1 ,y 1 ) and r = x 1 mod n. If r = 0 then go to step 1. Compute k -1 mod n. Compute e = SHA-1(m). Compute s = k -1 {e + d A . r} mod n. If s = 0 then go to step 1. A's signature for the message m is (r, s).

54. RS-RNSIT Elliptic Curve Digital Signature Algorithm (ECDSA) To verify A's signature (r, s) on m, B performs the following steps: Verify that r and s are integers in [1,n-1]. Compute e = SHA-1(m). Compute w = s -1 mod n. Compute u 1 = ew mod n and u 2 = rw mod n. Compute (x 1 ,y 1 ) = u 1 G+ u 2 Q A Compute v = x 1 mod n. Accept the signature if and only if v = r. SHA-1 denotes the 160-bit hash function

55. RS-RNSIT Analogue of the DSA, proposed by Scott Vanstone in 1992. To encrypt a message m for B, A performs : Select a random integer r from [1,n-1]. Compute R = rG. Compute K = hrQ B = (K X , K Y ). Check that K  O: Compute k 1 || k 2 = KDF(K X ). Compute c = (k 1 , m). Compute t = MAC(k 2 , c). Send (R; c; t) to B. ENC a symmetric encryption scheme such as Triple-DES MAC denotes a message authentication code (MAC) algorithm “ RFC 2104 ” ; KDF a key derivation function Elliptic Curve Authenticated Encryption Scheme (ECAES)

56. RS-RNSIT Elliptic Curve Authenticated Encryption Scheme (ECAES) To decrypt a ciphertext (R; c; t), B does: Perform a partial key validation on R. Compute K = hd B R = (K X , K Y ).. Check that that K  O: Compute k 1 || k 2 = KDF(K X ). Verify that t = MAC(k 2 , c). Compute m = ENC -1 (k 1 , c).

57. Why use ECC? How do we analyze Cryptosystems? How difficult is the underlying problem that it is based upon RSA – Integer Factorization DH – Discrete Logarithms ECC - Elliptic Curve Discrete Logarithm problem How do we measure difficulty? We examine the algorithms used to solve these problems RS-RNSIT

58. Advantages of ECC Hence, ECC offers equivalent security with much small key size. Practical advantages of ECC : 1 Faster 2 Low power consumption 3 Low memory usage 4 Low CPU utilization 5 Benefits of over its competitors increases with increase in the security needs.

59. Key References Papers: J. Lopez and R. Dahab, “Fast Multiplication on Elliptic Curves over GF(2 m ) without pre-computation”, CHES 1999 K. Fong etal, “Field Inversion and Point Halving Revisited”, IEEE Trans on Comp, 2004 G. Orlando and C. Paar, “A High Performance Reconfigurable Elliptic Curve Processor for GF(2 m )”, CHES 2000 N. A. Saqib etal, “A Parallel Architecture for Fast Computation of Elliptic Curve Scalar Multiplication over GF(2 m )”, Elsevier Journal of Microprocessors and Microsystems, 2004 Sabiel Mercurio etal, “ An FPGA Arithmetic Logic Unit for Computing Scalar Multiplication using the Half-and-Add Method”, IEEE ReConfig 2005

60. RS-RNSIT Key References Books: Elliptic Curves: Number Theory and Cryptography, by Lawrence C. Washington Guide to Elliptic Curve Cryptography, Alfred J . Menezes Guide to Elliptic Curve Cryptography, Darrel R. Hankerson , A . Menezes and A. Vanstone http://cr.yp.to/ecdh.html ( Daniel Bernstein)

61. RS-RNSIT Additional References : An Overview of Elliptic Curve Cryptography by Julio Lopez and Richard Dahab May 2000. http://citeseer.ist.psu.edu/lop00overview.html M. Abdalla, M. Bellare and P. Rogaway. “ DHAES: An encryption scheme on the Diffie- Hellman problem ” , preprint 1999 . http://www-cse.ucsd.edu/users/mihir / www.rsasecurity.com http://www.certicom.com/index.php?action=res,ecc_faq http://cgd.best.vwh.net/home/flt/flt03.htm http://mathworld.wolfram.com/EllipticCurve.html

62. RS-RNSIT Thank You !