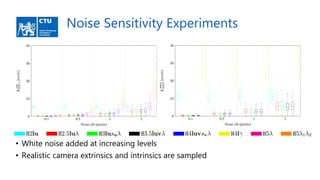
The document discusses a method for joint estimation of lens distortion and rectification, emphasizing the challenges of sampling distortion parameters and the non-convex nature of the problem. It introduces new solvers that utilize the hidden variable trick to reduce unknowns and improve the stability of solutions, while also addressing noise sensitivity in various scenarios. The findings indicate that the proposed solvers are more efficient and accurate compared to traditional methods.

1. Radially-Distorted Conjugate
Translations
James Pritts, Zuzana Kukelova, Viktor Larsson, Ondrej Chum
In CVPR 18

2. Motivation
• Joint estimation of lens distortion and rectification is needed for large
distortions
• Sampling lens distortion parameters during RANSAC increases sampling time
• Ex-post correction of lens distortion is difficult because problem is highly non-
convex
• Translations are common, minimal solvers require few correspondences
SequentialOriginal Joint

3. Inputs and Outputs
OriginalUndistortedRectifie
d
Narrow Medium Wide

4. Conjugate Translations

5. Incorporating the Division Model

6. Degrees of freedom
• Vanishing line has two degrees of freedom.
• Vanishing direction has two degrees of freedom.
• Unknown division model parameter .
• 5 degrees of freedom require 2.5 point correspondences.

7. Point-Coincidence Constraint
• Eliminate unknown homogeneous scalar
• Generates two linear independent equations, 2 constraints per
correspondence
• Orthogonality constraint

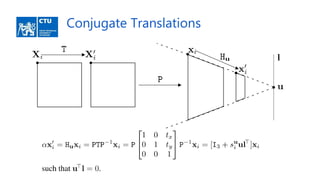
8. Solver Variants Generated
Reference [1] Proposed Minimal Solvers [2] [3] [4]
Undistorts ✓ ✓ ✓ ✓ ✓
Rectifies ✓ ✓ ✓ ✓ ✓ ✓
# points 2 2.5 3 3.5 4 4 5 5
Directions 1 1 1 2 2 2 1 1
# solutions 1 4 2 6 4 1 18 5
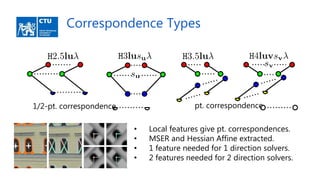
• One and two-direction variants of the proposed solvers are in colors.
• Each variant has a version that can rectify reflections (green, blue).

9. Correspondence Types
1/2-pt. correspondence pt. correspondence
• Local features give pt. correspondences.
• MSER and Hessian Affine extracted.
• 1 feature needed for 1 direction solvers.
• 2 features needed for 2 direction solvers.

10. Hidden Variable Trick
• Eliminating unknowns will simplify the generated solvers.
• The vanishing direction is linear and unknows can be hidden
in the coefficient matrix,
• Coefficients of are polynomials in .
• Thus all 4x4 sub-matrices of must have determinant 0.

11. Intuition for Solving Polynomial
Systems
• Solution with multiplicity 2 at
• We can write the system as a matrix equation

12. Represent polynomial system
in a more compact form as
Notational convenience

13. Adding and Eliminating Monomials
• Adding multiples of unknowns to original constraints does not add new
solutions.
• Provides additional linearly independent equations
• Eliminate monomials from rows by Gauss-Jordan elimination

14. Back Substitution
• Solve for
• Solving can be done numerically for higher order polynomials
• Back substitute
• Only finitely number of polynomials need to be added if the polynomial
system has rational coefficients and a finite number of solutions.
• The number of polynomials needed quickly explodes

15. Transfer Error
• Transfer error measures accuracy of the undistortion and conjugate
translation

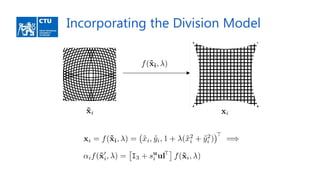
16. Comparison of Generated Solvers
z Original
(dashed)
Hidden
(solid)
80x84 14x18
74x76 24x26
348x354 54x60
730x734 76x80
Solvers based on constraints using the hidden variable trick are smaller and
more stable than solvers generated using [5] with the original constraints.

17. Warp Error
• Warp error (right) measures accuracy of undistortion and rectification.

18. Noise Sensitivity Experiments
• White noise added at increasing levels
• Realistic camera extrinsics and intrinsics are sampled

19. Narrow and Wide Angle results

20. Feature Problems

21. Robustness