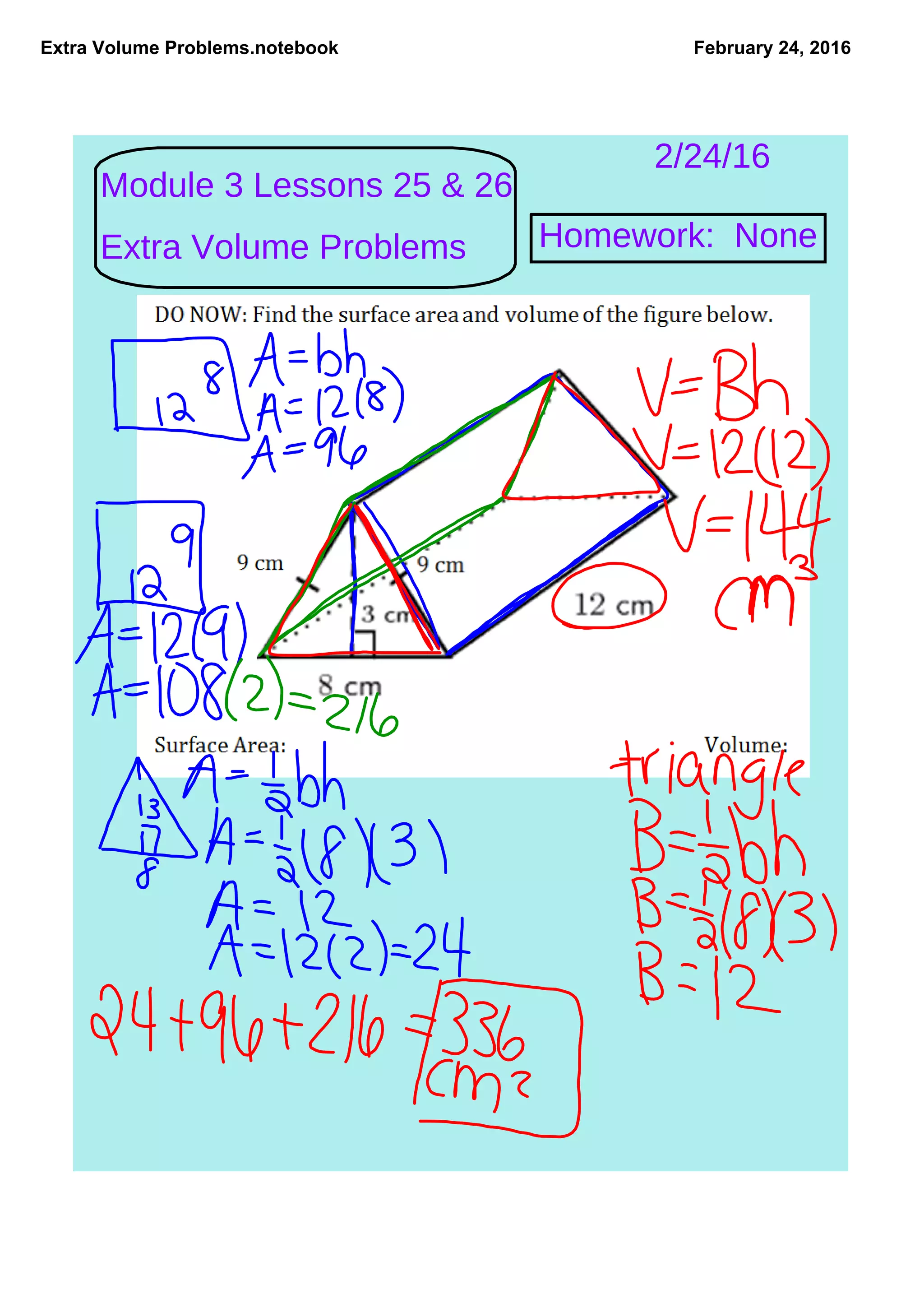
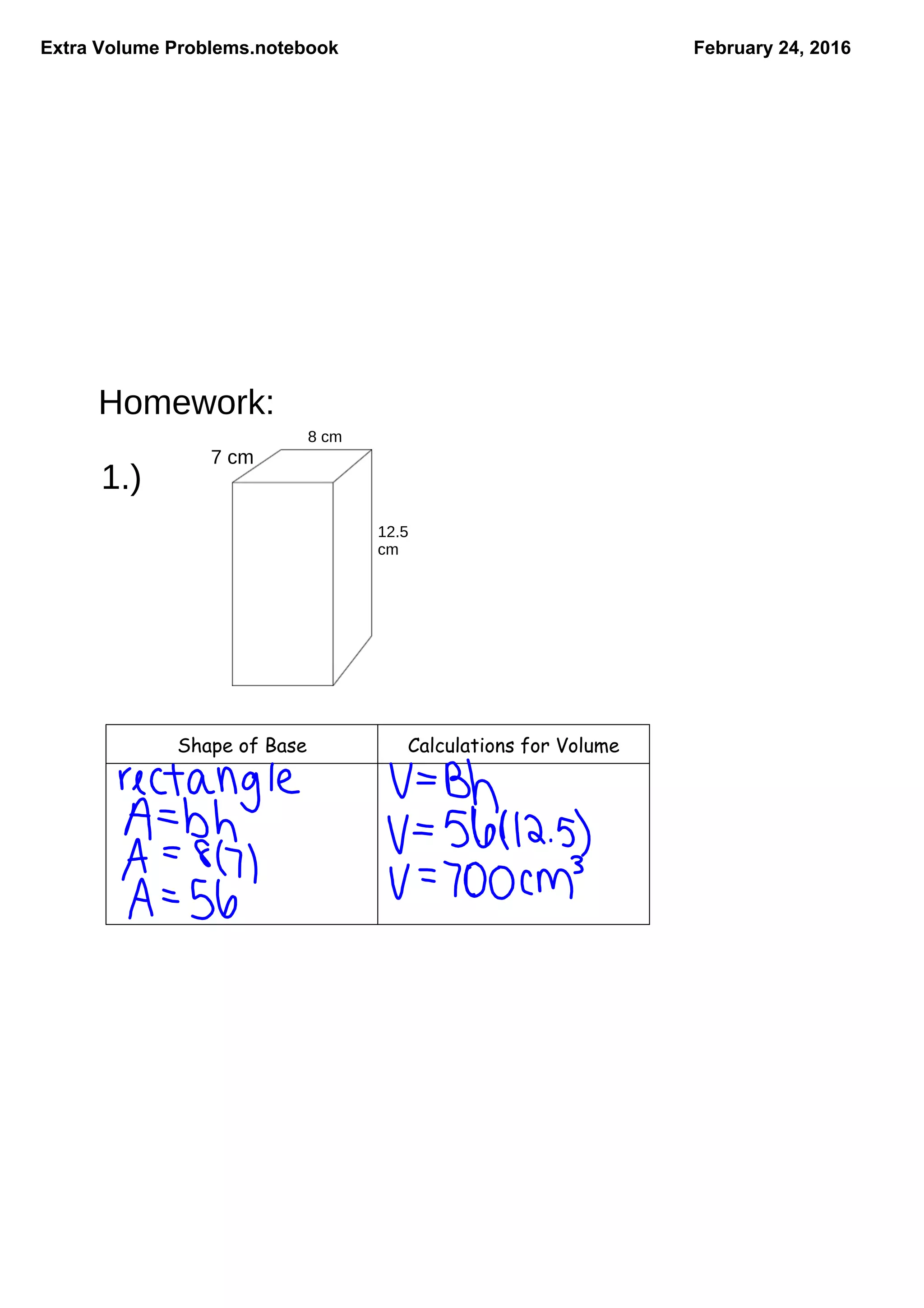
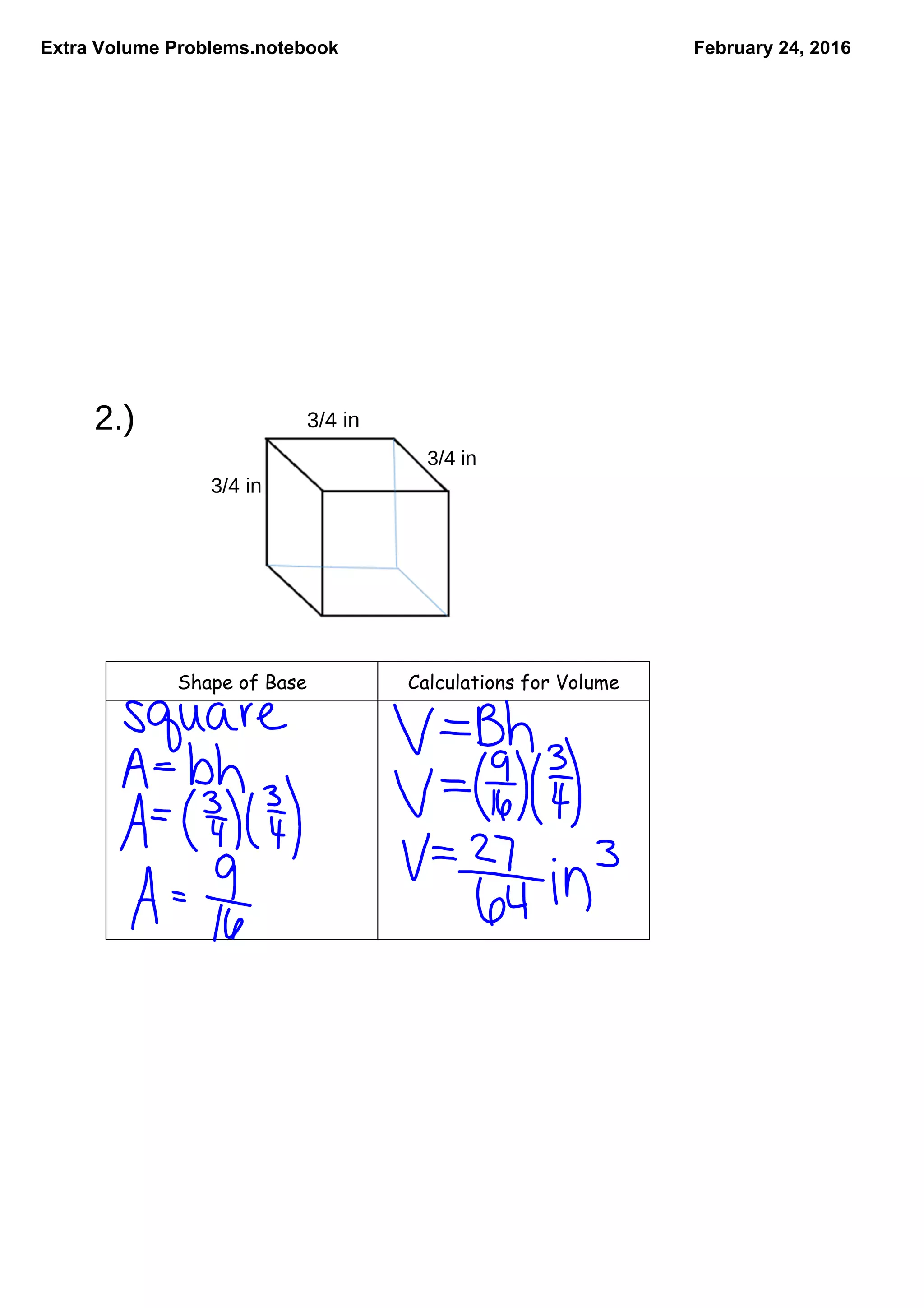
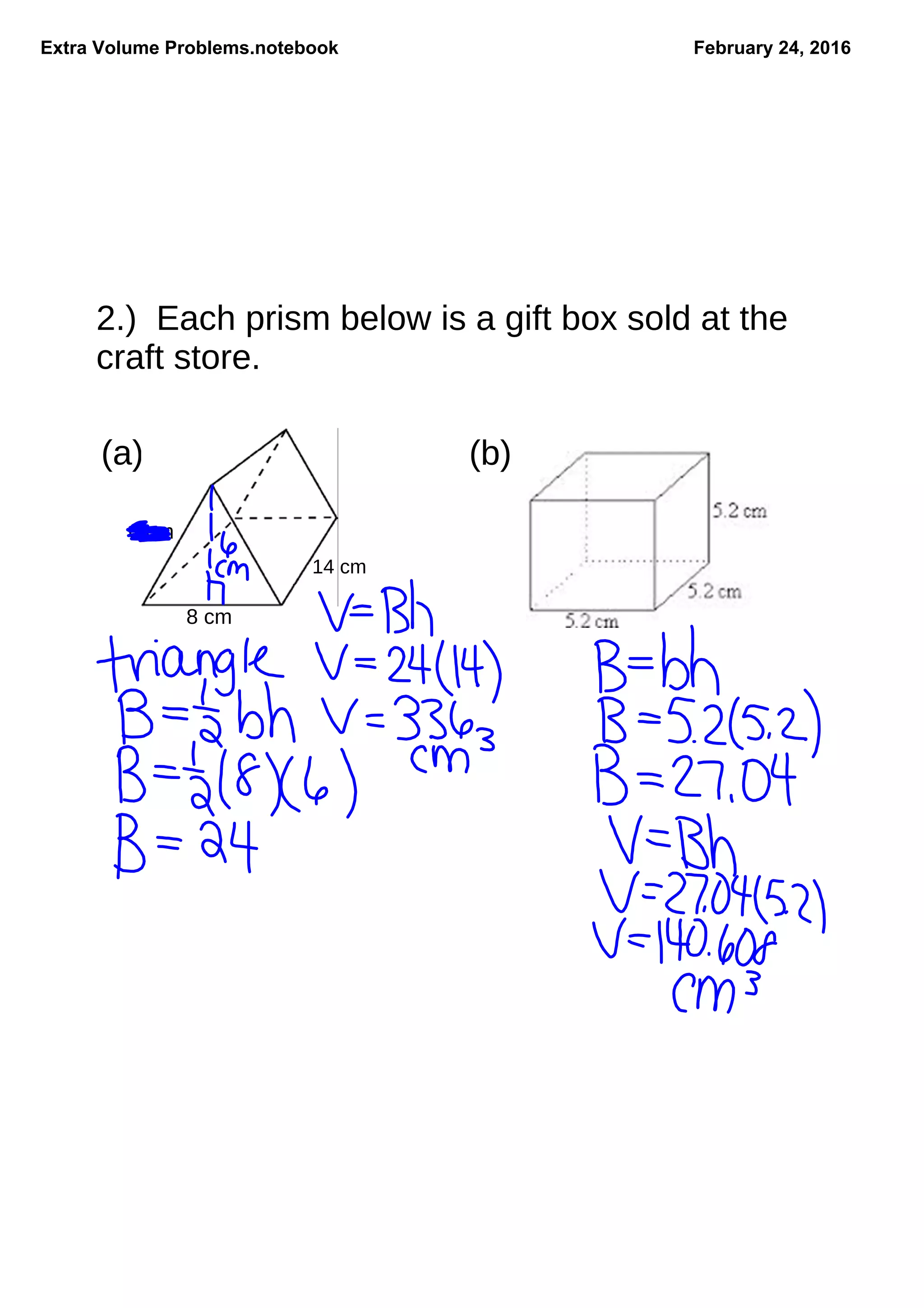
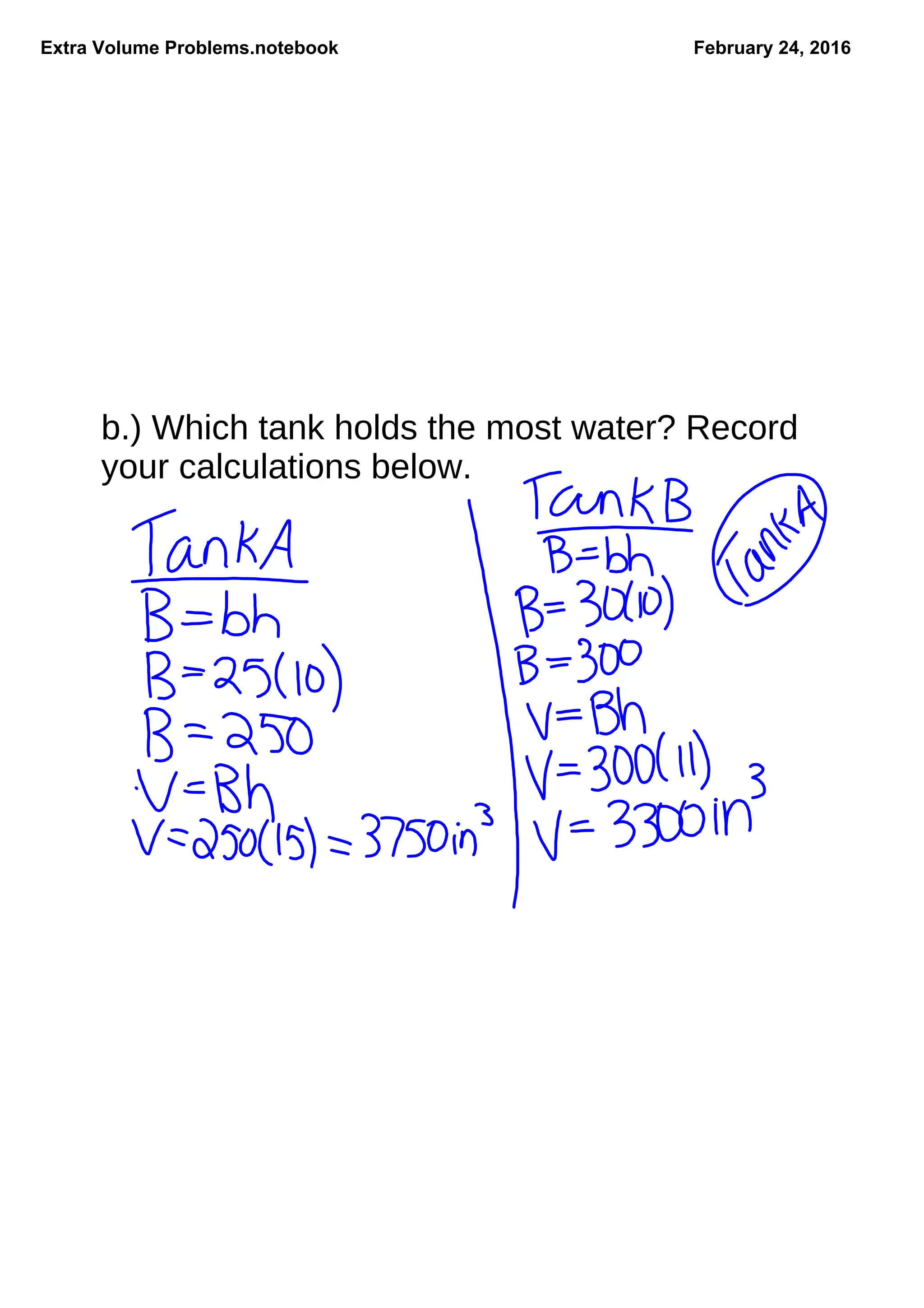The document contains extra volume problems for students to solve, focusing on various shapes including rectangular prisms and tanks. It presents practical scenarios such as calculating water capacity for fish tanks and estimating volumes for gift boxes. The exercises aim to enhance understanding of volume calculations in real-world contexts.

1. Extra Volume Problems.notebook February 24, 2016
Module 3 Lessons 25 & 26
Extra Volume Problems
2/24/16
Homework: None

2. Extra Volume Problems.notebook February 24, 2016
Homework:
1.)
8 cm
7 cm
12.5
cm
Shape of Base Calculations for Volume

3. Extra Volume Problems.notebook February 24, 2016
2.) 3/4 in
3/4 in
3/4 in
Shape of Base Calculations for Volume

4. Extra Volume Problems.notebook February 24, 2016
Find the volume of the following problems below.
1.) What is the volume of the right rectangular
prism?
10 cm
11 cm
6.5 cm

5. Extra Volume Problems.notebook February 24, 2016
2.)
a.) The diagrams below are two fish tanks. Ben
wants to figure out how much water each of them
hold. What is Ben going to need to do in order to
figure out how much water to two tanks hold?
Answer: __________________
Tank A
15 in
10 in
25 in
Tank B
30 in
10 in
11 in

6. Extra Volume Problems.notebook February 24, 2016
b.) Which tank holds the most water? Record
your calculations below.

7. Extra Volume Problems.notebook February 24, 2016
2.) Each prism below is a gift box sold at the
craft store.
(a)
14 cm
8 cm
6 cm
(b)

8. Extra Volume Problems.notebook February 24, 2016
(c) What is the volume of each prism?

9. Extra Volume Problems.notebook February 24, 2016
(d) Jen wants to fill each box with jelly beans. If
one ounce of jelly beans is approximately 30cm3,
estimate how many ounces of jelly beans Jen will
need to fill both boxes?

10. Extra Volume Problems.notebook February 24, 2016
3.) Marisa has a box that she has to fill with her
clothes. The dimensions of her box are 19 inches in
length, 9 inches in width, and 24 inches deep. How
much space does Marisa have in her box?

11. Extra Volume Problems.notebook February 24, 2016
From Yesterday's Notes
5.) Annie bought an aquarium that is a right rectangular prism.
The dimensions of the aquarium are 90 cm long, by 48 cm wide,
by 60 cm deep. She plans to pout water in the aquarium before
buying any pet fish. How many liters of water does she need to
put in the aquarium so that the water level is 5 cm below the top?
(1 L = 1000 cubic cm)