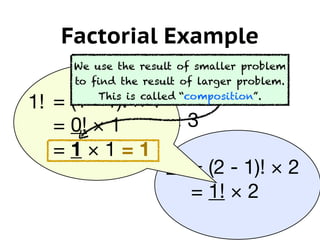
The document provides an overview of recursion in programming, particularly using Python as a teaching tool. It explains key concepts like decomposition, base case, and composition with examples of factorial calculations, the Euclidean algorithm, string reversal, and palindrome checking. Additionally, the document emphasizes the importance of recursion for writing clean and understandable code.






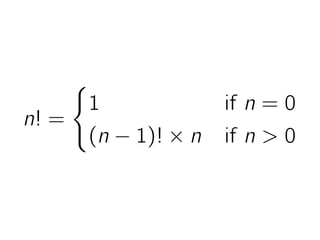













































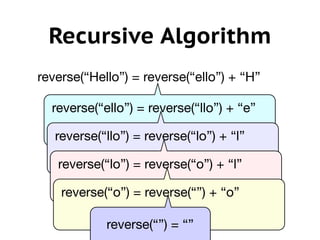





![Reverse Example
def reverse(str):
if str == "":
return str # or return “”
else:
return reverse(str[1:]) + str[0]
print reverse("reenigne")](https://image.slidesharecdn.com/recursionlecture-130627214326-phpapp02/85/Introduction-to-Recursion-Python-68-320.jpg)









![def is_palindrome(s):
if len(s) < 2:
return True
if s[0].lower() != s[-1].lower():
return False
return is_palindrome(s[1:-1])
print is_palindrome("Refer") # => True
print is_palindrome("Referrer") # => False](https://image.slidesharecdn.com/recursionlecture-130627214326-phpapp02/85/Introduction-to-Recursion-Python-78-320.jpg)
![def is_palindrome(s):
return reverse(s.lower()) == s.lower()
print is_palindrome("Refer") # => True
print is_palindrome("Referrer") # => False
def reverse(str):
if str == "":
return str
else:
return reverse(str[1:]) + str[0]](https://image.slidesharecdn.com/recursionlecture-130627214326-phpapp02/85/Introduction-to-Recursion-Python-79-320.jpg)
