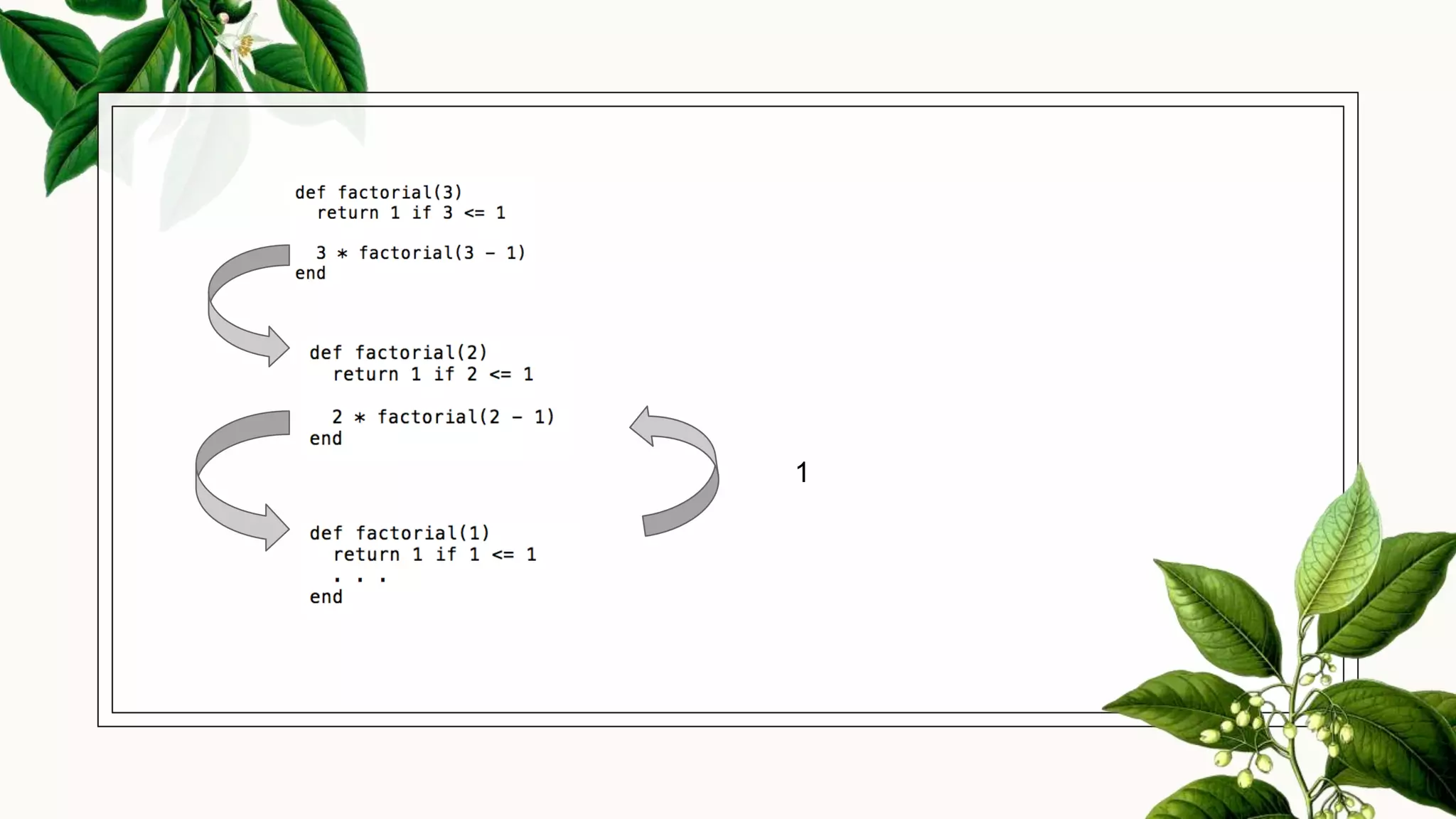
Recursion is defined as a function that calls itself. It solves a larger problem by breaking it down into smaller instances of the same problem. A recursive function must have a base case, where it stops calling itself, and it builds solutions up the call stack until the base case is reached. Examples of recursive functions include calculating factorials, Fibonacci sequences, and tree/graph traversals. While powerful, recursion risks stack overflow errors if not implemented properly.