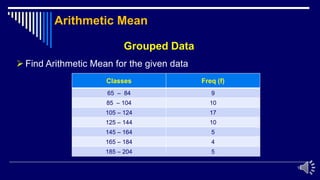
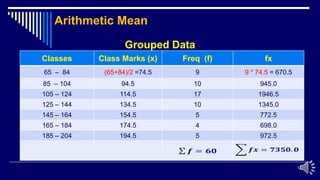
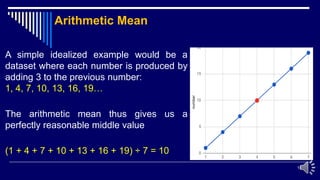
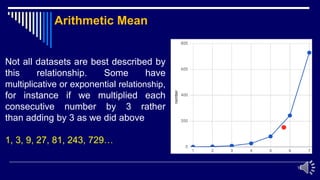
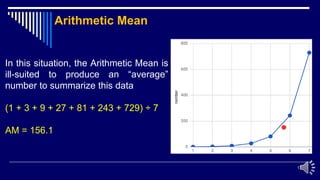
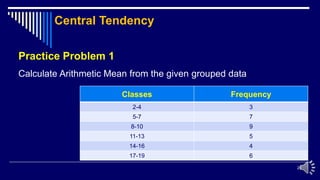
This document provides an overview of measures of central tendency, specifically focusing on the arithmetic mean. It defines the arithmetic mean and how to calculate it for both ungrouped and grouped data. For grouped data, the class marks and frequencies are used to calculate a weighted sum. Examples are provided to demonstrate calculating the arithmetic mean from raw data and grouped frequency tables. Situations when the arithmetic mean is appropriate versus when other averages like the geometric mean are better suited are also discussed. Practice problems are included to calculate arithmetic means from various data sets.