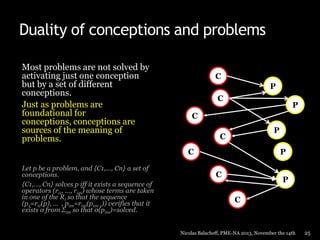
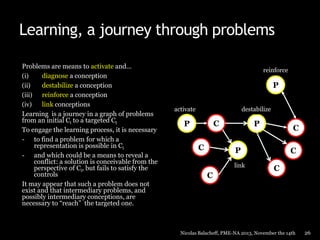
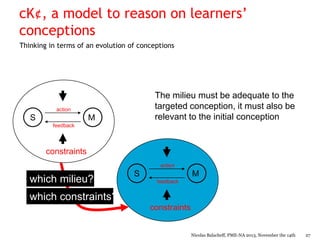
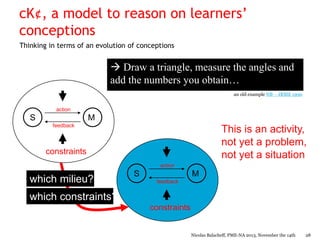
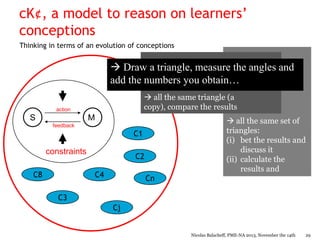
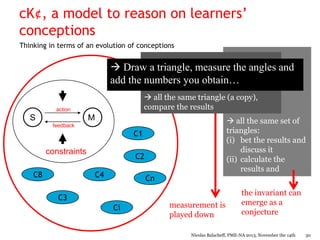
Nicolas Balacheff explores the complexities of mathematical understanding and learner conceptions from both didactical and developmental perspectives. He argues that errors made by learners often reflect reasoned attempts to comprehend situations rather than mere misconceptions, proposing that understanding is tied to behaviors shaped by the learning environment. The document delves into the interactions between a learner's cognitive and emotional characteristics and their environment, emphasizing the role of context in shaping knowledge and conceptions.

1. Nicolas Balacheff
CNRS - Laboratoire d’Informatique de Grenoble
Nicolas.balacheff@imag.fr
cK¢, A MODEL TO REASON ON
LEARNERS’ CONCEPTIONS

2. Understanding learners’ understanding
“Asking a student to understand something means asking a
teacher to assess whether the student has understood it.
But what does mathematical understanding look like?”
(Common core state standard initiative retrieved 11/10/13)
With the objective of contributing to a response , I start from the following two
theoretical postulates:
From a didactical perspective teaching design consists of
producing a game specific to the target knowledge among
different subsystems: the educational system, the student
system, the milieu, etc.
(Brousseau 1986)
From a developmental perspective, a concept is altogether: a set of
situations, a set of operational invariants, and a set of linguistic
and symbolic representations.
(Vergnaud 1980)
Nicolas Balacheff, PME-NA 2013, November the 14th
2

3. Note about the vocabulary (1)
Misconceptions, naïve theories, beliefs have been largely documented in an attempt
to make sense of learners’ errors and contradictions
« ƒ is defined by f(x) = lnx + 10sinx
Is the limit + in + ? »
with a graphic calculator 25% of errors
without a graphic calculator 5% of errors
(Guin & Trouche 2001)
Decisions are situated
Distributed in space and time decisions which are never brought face to face in
practice are practically compatible even if they are logically contradictory
(paraphrasing Bourdieu)
Contradictions and errors appear when learners are involved in situations
foreign to their actual practice but in which they have to produce a response
Nicolas Balacheff, PME-NA 2013, November the 14th
3

4. Note about the vocabulary (2)
“many times a child’s response is labeled erroneous too quickly
and […] if one were to imagine how the child was making sense of
the situation, then one would find the errors to be reasoned and
supportable” (Confrey 1990 p.29).
Learners have conceptions which are adapted and efficient in
different situations they are familiar with. They are not naïve or
misconceived, nor mere beliefs. They are situated and
operational in the adequate circumstances.
They have the properties of a piece of knowledge.
 Knowledge is a difficult English word which can refer to implicit or
explicit mental constructs, it can express the familiarity of someone
with something or be authoritative with a theoretical status.
Instead of “knowledge” I will use “knowing” as a noun, leaving
“knowledge” for those “knowings” which have a social and institutional
status.
Nicolas Balacheff, PME-NA 2013, November the 14th
4

5. Behaviors and understanding
 what does mathematical understanding look like?”
understanding cannot be reduced to behaviors, whereas it
cannot be characterized without linking it to behaviors
This is a classical feature in psychology
A behavior is
- a product of mental acts (ways of understanding)
(Harel 1998)
- a component in an activity (it is intentional)
- a response to a situation (it is situated)
it has explicit (what) and implicit (why) dimensions
- a construct not a given
Nicolas Balacheff, PME-NA 2013, November the 14th
5

6. Behaviors and understanding
 what does mathematical understanding look like?”
understanding cannot be reduced to behaviors, whereas it
cannot be characterized without linking it to behaviors
This is a classical feature in psychology
A behavior is
- a product of mental acts (ways of understanding)
(Harel 1998)
-
a component in an activity (it is intentional)
a response to a situation (it is situated)
problems as revealers of
mathematical understanding
Nicolas Balacheff, PME-NA 2013, November the 14th
6

7. the “learner/milieu system”
A learner is first a person with her
emotions, social
commitments, imagination, personal
history, cognitive characteristics. He or she
lives in a complex environment
which has physical, social and symbolic
characteristics.
However, for the sake of the modeling objective
and with in mind the practical limitations is will
entail…
action
M
S
feedback
constraints
Learners are considered here as the
epistemic subjects
The environment is reduced to those features
that are relevant from an epistemic perspective:
the milieu
the learner’s antagonist system in the learning process
Nicolas Balacheff, PME-NA 2013, November the 14th
7

8. the “learner/milieu system”
A learner is first a person with her
emotions, social
commitments, imagination, personal
history, cognitive characteristics. He or she
lives in a complex environment
which has physical, social and symbolic
characteristics.
However, for the sake of the modeling objective
and with in mind the practical limitations is will
entail…
Learners are considered here as the
epistemic subjects
The environment is reduced to those features
that are relevant from an epistemic perspective:
the milieu
the learner’s antagonist system in the learning process
action
M
S
feedback
constraints
A conception is the state of
dynamical equilibrium of an
action/feedback loop between
a learner and a milieu under
proscriptive constraints of
viability
Nicolas Balacheff, PME-NA 2013, November the 14th
8

9. Conception (2) a characterization
a “conception” is
characterized by a
quadruplet (P, R, L, Σ)
where:
 P is a set of problems.
action
M
S
feedback
constraints
 R is a set of operators.
 L is a representation system.
 Σ is a control structure.
the quadruplet is not more related to S than M: the representation system allows the formulation
and use of operators by the active sender (the learner) as well as the reactive receiver (the milieu);
the control structure allows assessing action, as well as selecting a feedback.
Nicolas Balacheff, PME-NA 2013, November the 14th
9

10. Addition, from fingers to keystrokes
C1: Verbal counting IIIII & III
P – Quantify union of two sets, objects are
physically present, both cardinals are small.
R – match fingers or objects and number
names, pointing objects
L – body language, counting
Σ – not counting twice the same, counting
all, order of the number names
C 2: Counting on 15+8
P – The numbers are given, but the
collections are not present, one of the
numbers must be small enough
R – choose the greater number, count-on to
determine the result.
L – body language, number naming, verbal
counting.
Σ – order of the number names , match
fingers to number names
C3: written addition 381+97
P – adding two integers
R – algorithm of column addition
L – decimal representation of
numbers
Σ – check the implementation of the
algorithm, check the layout of
number addition
C4: Pocket calculator
P – adding two integers
R – keystroke to represent a number, to
process number addition
L – body language (keystrokes), decimal
representation of numbers on the screen
Σ – keystrokes verification, order of
magnitude.
Nicolas Balacheff, PME-NA 2013, November the 14th
10

11. Addition, from fingers to keystrokes
C1: Verbal counting IIIII & III
P – Quantify union of two sets, objects are
physically present, both cardinals are small.
R – match fingers or objects and number
names, pointing objects
L – body language, counting
Σ – not counting twice the same, counting
all, order of the number names
prototype: “You have 5 pebbles, I give
you 3 more, how many
have you now?”
Couting-all means reciting the nursery rythme
while matching one-to-one words and objects
Nicolas Balacheff, PME-NA 2013, November the 14th
11

12. Addition, from fingers to keystrokes
prototype: “You have 15 pebbles, I give
you 8 more, how many do
have you now?”
Ability to produce the correct sequence of
counting words beginning from an arbitrary point
in the sequence, manage the « cardinal meaning »
and the « counting meaning » of number words
(K. Fuson)
C 2: Counting on 15+8
P – The numbers are given (collections are
not present), one of the numbers must be
small enough
R – choose the greater number, count-on to
determine the result.
L – body language, number naming, verbal
counting.
Σ – order of the number names , match
fingers to number names
Nicolas Balacheff, PME-NA 2013, November the 14th
12

13. Addition, from fingers to keystrokes
C3: written addition 381+97
P – adding two integers
R – algorithm of column addition
L – decimal representation of
numbers
Σ – check the implementation of the
algorithm, check the layout of
number addition
-
A number is composed of digits
Digits have a place-value
Link number names and written marks
Treat columns from right to left
To put and carry digits
most controls lies in
the symbolic register
Nicolas Balacheff, PME-NA 2013, November the 14th
13

14. Addition, from fingers to keystrokes
Keystroke might be faulty, result is bound by
the size of the screen, control rests in checking
the order of magnitude.
“along with the ability to use and interpret the results
obtained from the calculators there is a general
agreement that a greater facility in mental arithmetic
should be encouraged” (NCTM 1997)
C4: Pocket calculator
P – adding two integers
R – keystroke to represent a number, to
process number addition
L – body language (keystrokes), decimal
representation of numbers on the screen
Σ – keystrokes verification, order of
magnitude
Nicolas Balacheff, PME-NA 2013, November the 14th
14

15. Addition, from fingers to keystrokes
operators  actions at the interface of the
learner/milieu system;
representation system  semiotic means to
represent problems, support interaction and
represent operators
set of problems  problems for which the
conception provides efficient means
control structure  making choices, assessing
action and feedback, taking decisions, judging the
advancement of the problem or task
Nicolas Balacheff, PME-NA 2013, November the 14th
15

16. Arithmetic, from fingers to keystrokes
C is more general than C’ if it
exists a function of representation
ƒ: L’→L so that ∀p ∈P’, ƒ(p)∈P
Nicolas Balacheff, PME-NA 2013, November the 14th
16

17. The challenge of translation
Egyptian computation of 10 times 1/5
What is denoted by the signs are parts of
the whole, hence integers but integers
which could not be added as integers are.
Scribes used tables to establish the
correspondence between two numbers to
be multiplied and the result.
for 4055/4093 one will get the shortest and unique
additive decomposition:
[1/2 + 1/3 + 1/7 + 1/69 + 1/30650 + 1/10098761225]
Unfortunately, Egyptians could not write the last term.
Nicolas Balacheff, PME-NA 2013, November the 14th
17

18. Questioning controls to understand
representations
Construct a circle with AB as a
diameter. Split AB in two equal
parts, AC and CB. Then
construct the two circles of
diameter AC and CB… and so on.
How does the perimeter
vary at each stage?
How does the area vary?
A
C
B
Pedemonte 2002
Nicolas Balacheff, PME-NA 2013, November the 14th
18

19. Questioning controls to understand
representations
31. Vincent : the area is always divided by
2…so, at the limit? The limit is a
line, the segment from which we
started …
32. Ludovic : but the area is divided by two each
time
33. Vincent : yes, and then it is 0
34. Ludovic : yes this is true if we go on…
37. Vincent : yes, but then the perimeter … ?
38. Ludovic: no, the perimeter is always the
same
41. Vincent: It falls on the segment… the circles
are so small.
42. Ludovic: Hmm… but it is always 2πr.
43. Vincent: Yes, but when the area tends to 0 it
will be almost equal…
44. Ludovic: No, I don’t think so.
45. Vincent: If the area tends to 0, then the
perimeter also… I don’t know…
46. Ludovic: I will finish writing the proof.
A
B
Pedemonte 2002
Construct a circle with AB as a diameter. Split AB in two
equal parts, AC and CB. Then construct the two circles of
diameter AC and CB… and so on.
How does the perimeter vary at each stage?
How does the area vary?”
Nicolas Balacheff, PME-NA 2013, November the 14th
19

20. Questioning controls to understand
representations
31. Vincent : the area is always divided by
2…so, at the limit? The limit is a
line, the segment from which we
started …
32. Ludovic : but the area is divided by two each
time
33. Vincent : yes, and then it is 0
34. Ludovic : yes this is true if we go on…
37. Vincent : yes, but then the perimeter … ?
38. Ludovic: no, the perimeter is always the
same
41. Vincent: It falls on the segment… the circles
are so small.
42. Ludovic: Hmm… but it is always 2πr.
43. Vincent: Yes, but when the area tends to 0 it
will be almost equal…
44. Ludovic: No, I don’t think so.
45. Vincent: If the area tends to 0, then the
perimeter also… I don’t know…
46. Ludovic: I will finish writing the proof.
A
B
Pedemonte 2002
Construct a circle with AB as a diameter. Split AB in two
equal parts, AC and CB. Then construct the two circles of
diameter AC and CB… and so on.
How does the perimeter vary at each stage?
How does the area vary?”
Nicolas Balacheff, PME-NA 2013, November the 14th
20

21. Questioning controls to understand
representations
Algebraic frame
The symbolic
representation works
as a boundary object
adapting the different
meanings but being
robust enough to work
as a tool for both
students.
Ludovic
Algebraic
conception
formula
Vincent
symbolic-arithmetic
conception
area /perimeter
The differences lie in
the control grounding
their activity.
Nicolas Balacheff, PME-NA 2013, November the 14th
21

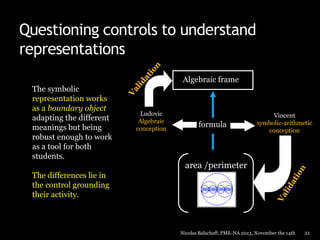
22. Controls and representation
A
B
D
C
A method used by sugar-cane farmers in
Brazil to find the areas of their fields were
to find the average lengths of the opposite
sides and multiply the averages together.
Guida de Abreu
S = [(AB+DC)/2]x[(AD+BC)/2]
C is false from the point of view of C’ if it exists a function of
representation ƒ: L→L’, and it exists [p∈P, r∈R, σ∈Σ, σ’∈Σ’] so
that σ(r(p))=true and σ’(ƒ(r(p))=false
“Generality” and “falsity” are not properties of conceptions but relations between
two conceptions whose validity depends on the translation from one system of
representation to the other.
This is often hidden by the fact that we tend to read the production
and the processes learners carry out directly in mathematical terms.
Nicolas Balacheff, PME-NA 2013, November the 14th
22

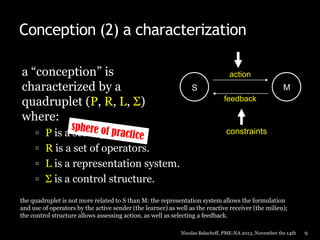
23. Conception, knowing and concept
Are the conception we diagnose and the one we “hold” referring to the
same “object”?
Difficult in mathematics where the only tangible things we manipulate are
representations, but Vergnaud’s postulate (1981) offers a solution:
problems are sources and criteria of knowing
Let C, C’ and Ca be three conceptions such that it exists functions of
representation ƒ: L→La and ƒ’: L’→La
[C and C’ have the same object with respect to Ca if for all p from
P it exists p’ from P’ such that ƒ(p)=ƒ’(p’), and reciprocally]
Conceptions have the same object if their spheres of practice can be
matched from the point of view of a more general conception
 which in our case is the conception of the researcher/teacher
Nicolas Balacheff, PME-NA 2013, November the 14th
23

24. Conception, knowing and concept
“To have the same object with respect to a conception Ca” sets
an equivalence relation among conceptions.
Let’s now claim the existence of a conception Cµ more general
than any other conception to which it can be compared
(pragmatically this is the role of a piece of a mathematical theory as a reference)
A “concept” is the set of all conceptions having
the same object with respect to Cµ.
This definition is aligned with the idea that a mathematical concept is not
reduced to the text of its formal definition, but is the product of its history
and of practices in different communities, esp. the mathematical one.
A “knowing” is any set of conceptions.
In other words: a conception is the instantiation of a knowing by a
situation (it characterizes the subject/milieu system in a situation) or a
conception is the instantiation of a concept by a pair (subject/situation).
Nicolas Balacheff, PME-NA 2013, November the 14th
24

25. Duality of conceptions and problems
Most problems are not solved by
activating just one conception
but by a set of different
conceptions.
Just as problems are
foundational for
conceptions, conceptions are
sources of the meaning of
problems.
C
P
C
P
C
P
C
C
Let p be a problem, and {C1,…, Cn} a set of
conceptions.
{C1,…, Cn} solves p iff it exists a sequence of
operators (ri1, …, rim) whose terms are taken
in one of the Ri so that the sequence
(p1=ri1(p), … , pim=rim(pim-1)) verifies that it
exists σ from Σim so that σ(pim)=solved.
P
C
P
C
Nicolas Balacheff, PME-NA 2013, November the 14th
25

26. Learning, a journey through problems
Problems are means to activate and…
(i)
diagnose a conception
(ii)
destabilize a conception
(iii)
reinforce a conception
(iv)
link conceptions
Learning is a journey in a graph of problems
from an initial Ci to a targeted Ct
To engage the learning process, it is necessary
to find a problem for which a
representation is possible in Ci
and which could be a means to reveal a
conflict: a solution is conceivable from the
perspective of Ci, but fails to satisfy the
controls
It may appear that such a problem does not
exist and that intermediary problems, and
possibly intermediary conceptions, are
necessary to “reach” the targeted one.
reinforce
P
activate
destabilize
C
P
C
P
C
P
link
C
C
C
Nicolas Balacheff, PME-NA 2013, November the 14th
26

27. cK¢, a model to reason on learners’
conceptions
Thinking in terms of an evolution of conceptions
The milieu must be adequate to the
targeted conception, it must also be
relevant to the initial conception
action
S
M
feedback
constraints
action
which milieu?
S
M
feedback
which constraints?
constraints
Nicolas Balacheff, PME-NA 2013, November the 14th
27

28. cK¢, a model to reason on learners’
conceptions
Thinking in terms of an evolution of conceptions
 Draw a triangle, measure the angles and
add the numbers you obtain…
an old example NB – JRME 1990
action
S
M
feedback
This is an activity,
not yet a problem,
not yet a situation
constraints
action
which milieu?
S
M
feedback
which constraints?
constraints
Nicolas Balacheff, PME-NA 2013, November the 14th
28

29. cK¢, a model to reason on learners’
conceptions
Thinking in terms of an evolution of conceptions
 Draw a triangle, measure the angles and
add the numbers you obtain…
 all the same triangle (aan old example NB – JRME 1990
copy), compare the results
action
S
M
feedback
C1
constraints
C8
C2
C4
Cn
 all the same set of
triangles:
(i) bet the results and
discuss it
(ii) calculate the
results and
compare
C3
Cj
Nicolas Balacheff, PME-NA 2013, November the 14th
29

30. cK¢, a model to reason on learners’
conceptions
Thinking in terms of an evolution of conceptions
 Draw a triangle, measure the angles and
add the numbers you obtain…
 all the same triangle (a copy),
compare the results
action
S
M
 all the same set of
triangles:
(i) bet the results and
discuss it
(ii) calculate the
results and
compare
feedback
C1
constraints
C8
C2
C4
Cn
C3
Ci
measurement is
played down
the invariant can
emerge as a
conjecture
Nicolas Balacheff, PME-NA 2013, November the 14th
30

31. cK¢ proposes a modeling framework to provide an
analytical tool to respond to the question:
What does mathematical understanding look like?
cK¢ dares a formalism as a unifying tool to
enhance the way we
inform the design of learning material and
learning situations, including technology
enhanced learning environments
Yet, cK¢ holds other promises:
building a bridge between knowing and proving
by constructing links between control and proof.
but this is an other story…
Nicolas Balacheff, PME-NA 2013, November the 14th
31

32. Open access to…
Slide-show on
SlideShare
Text on arXiv
Nicolas Balacheff, PME-NA 2013, November the 14th
32