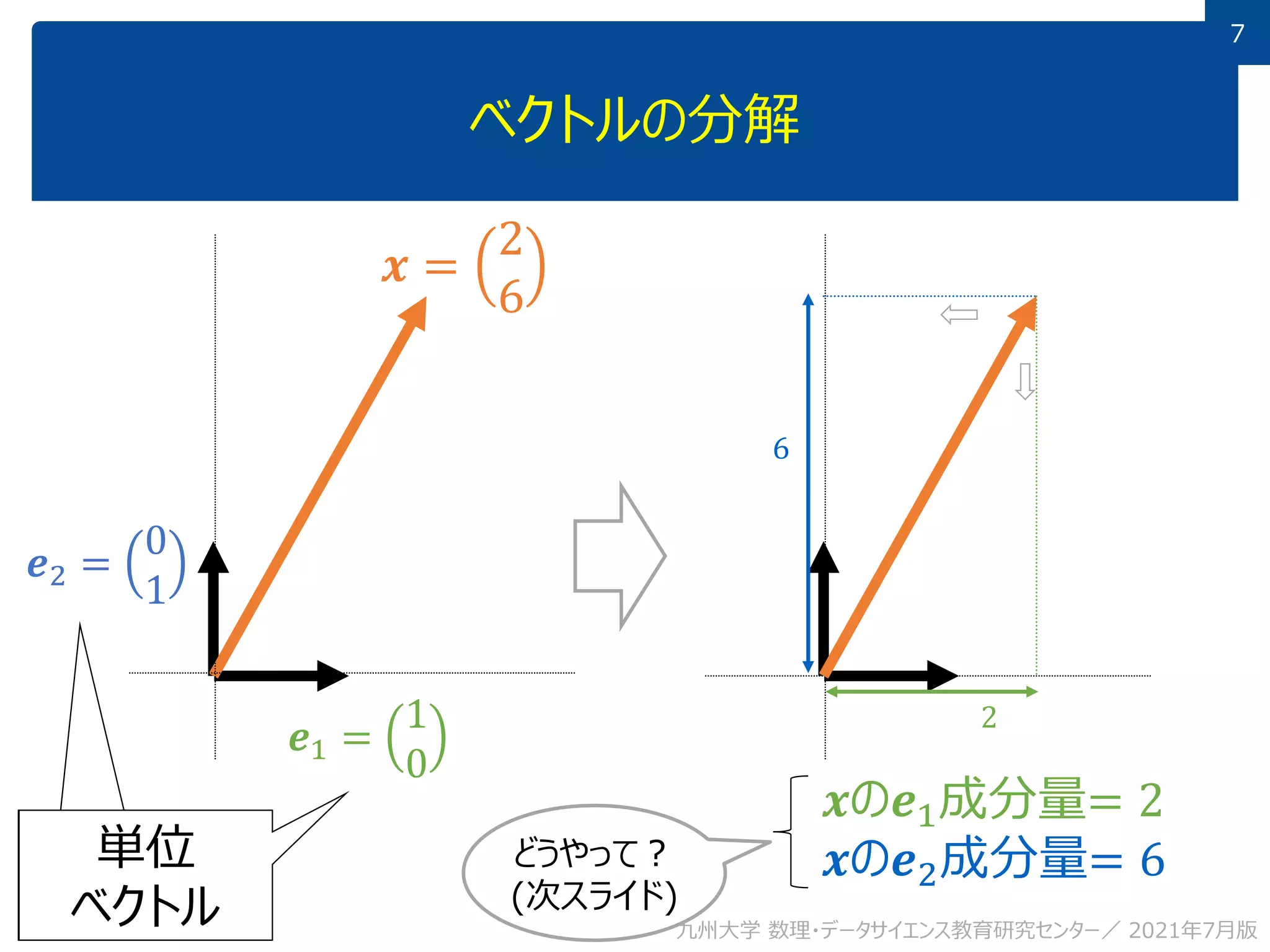
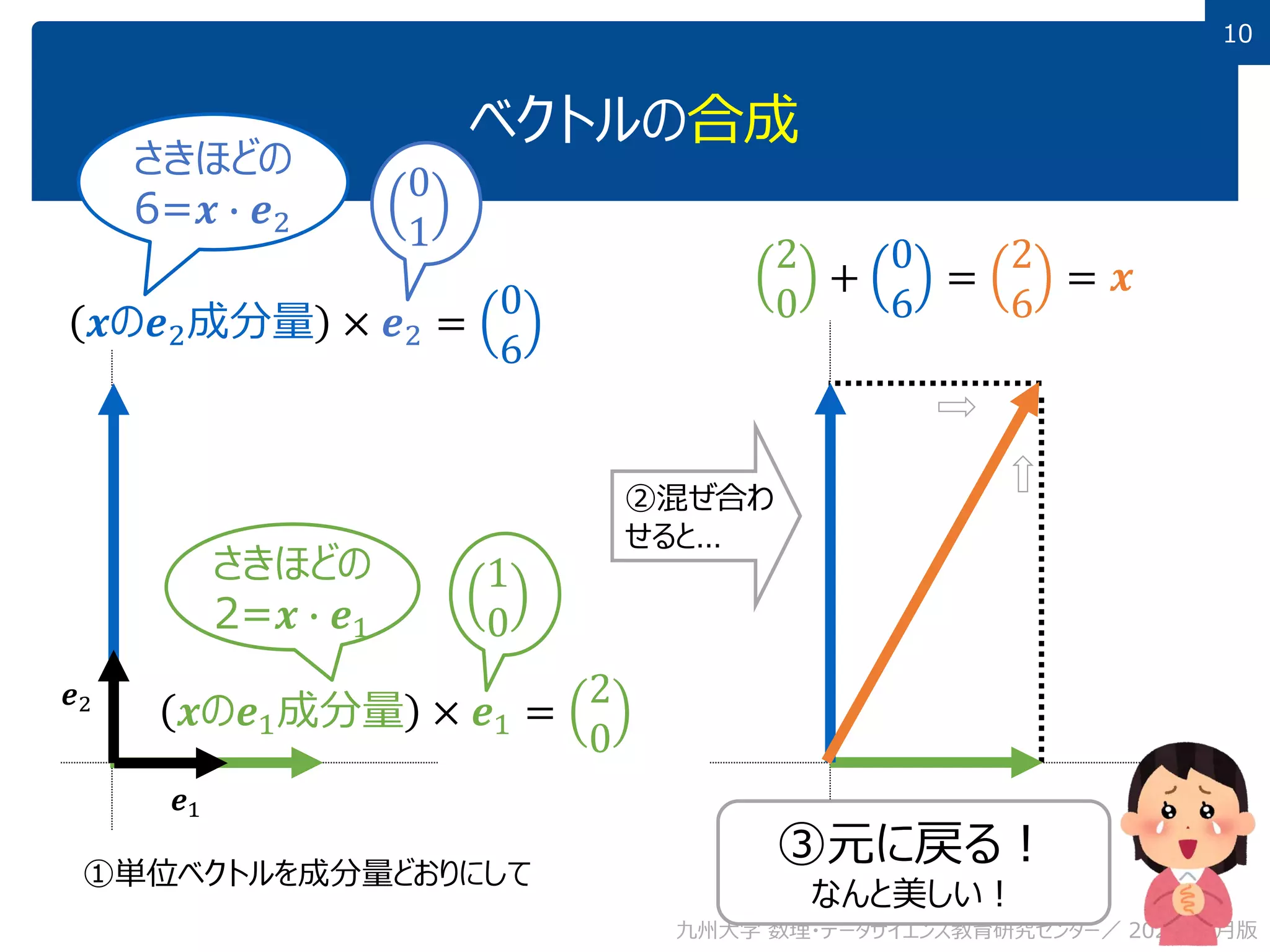
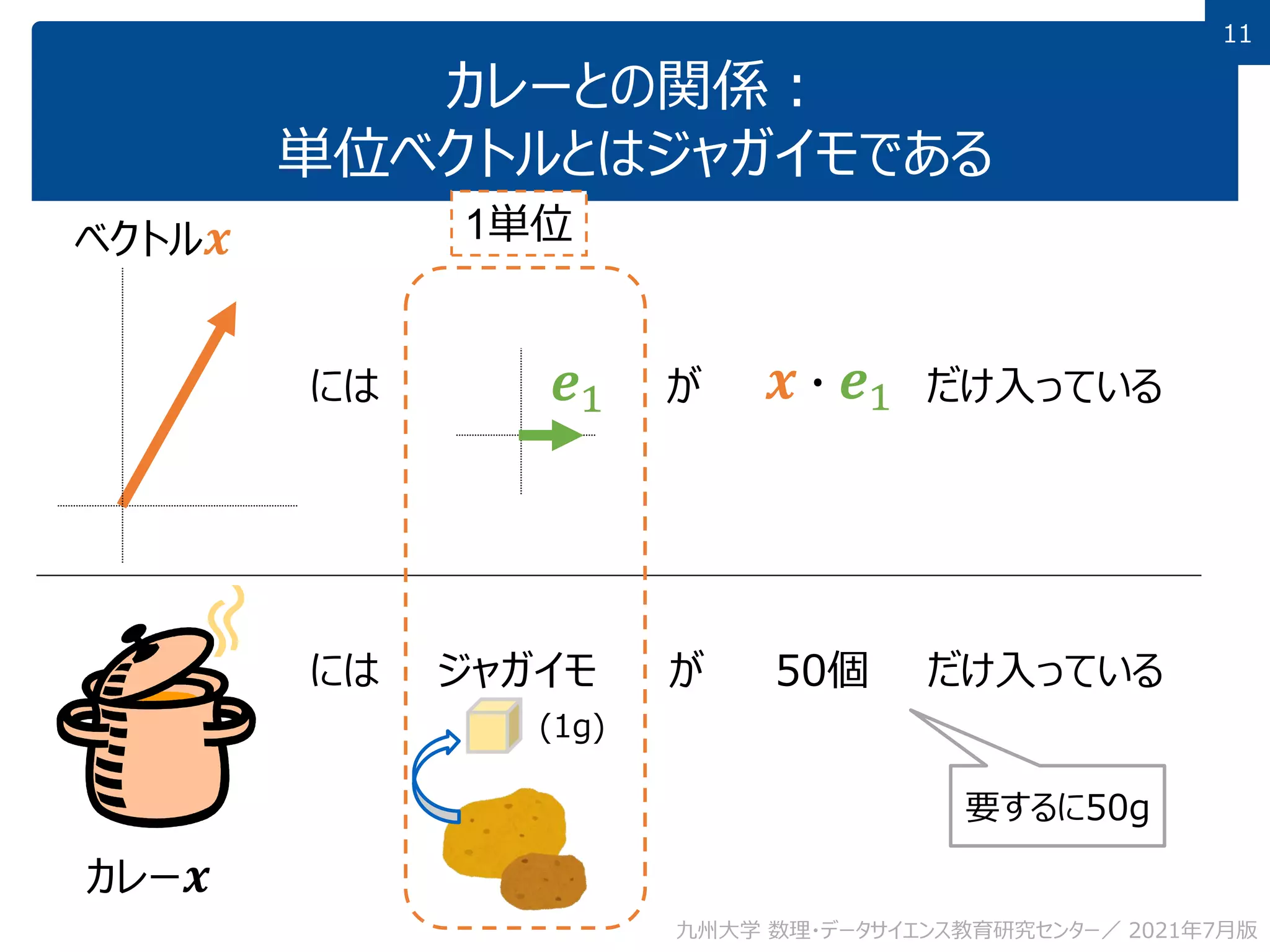
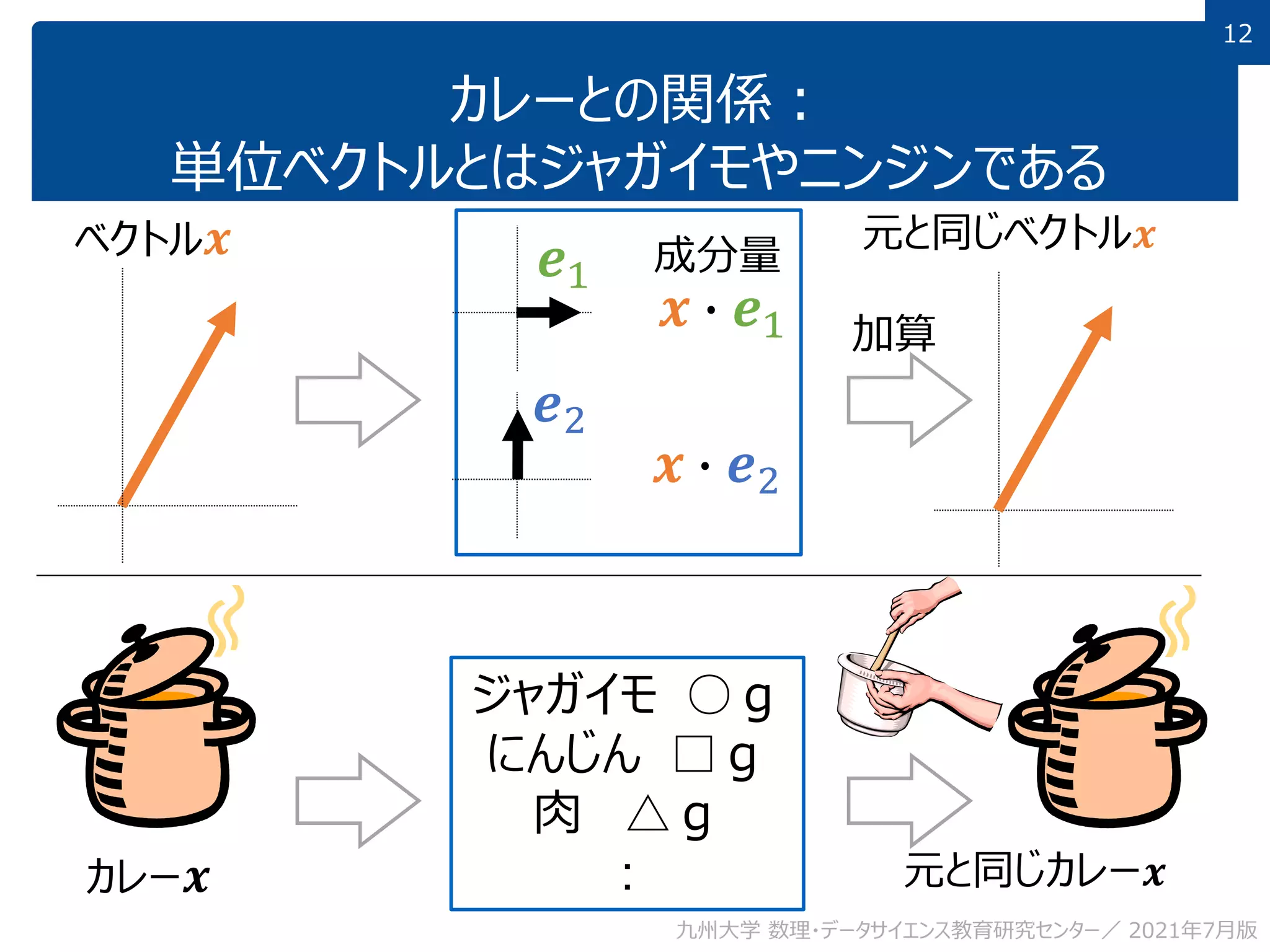
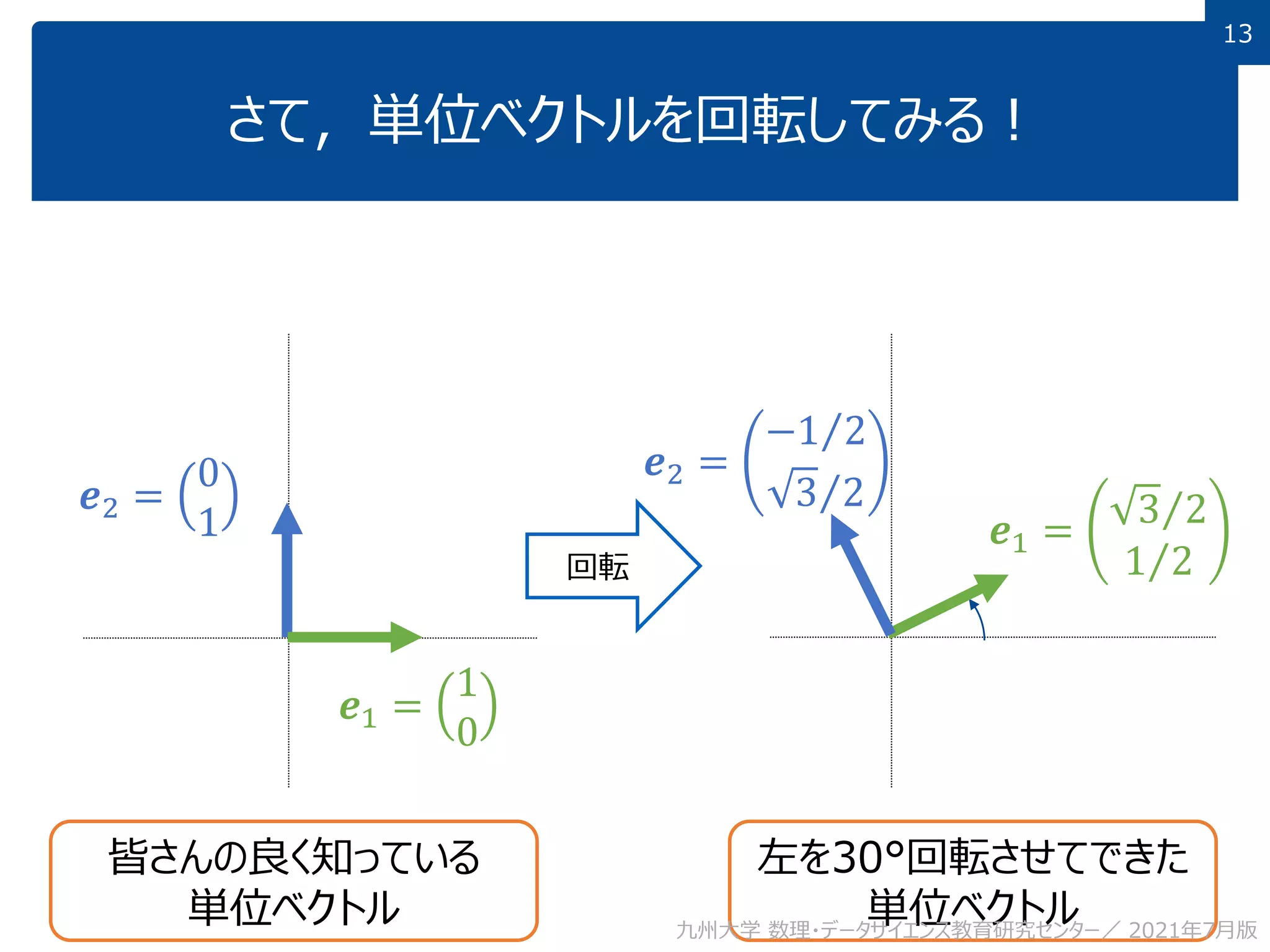
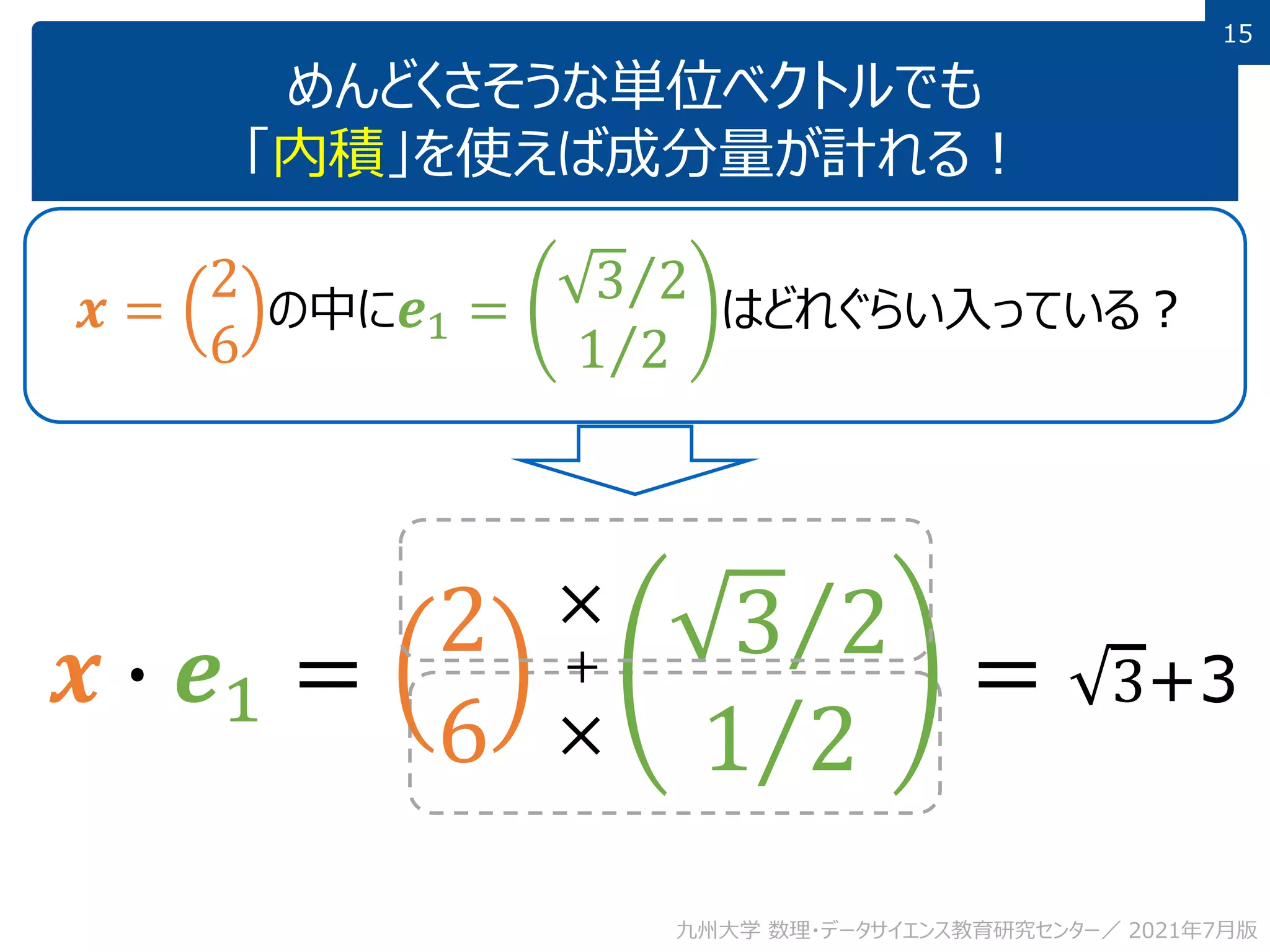
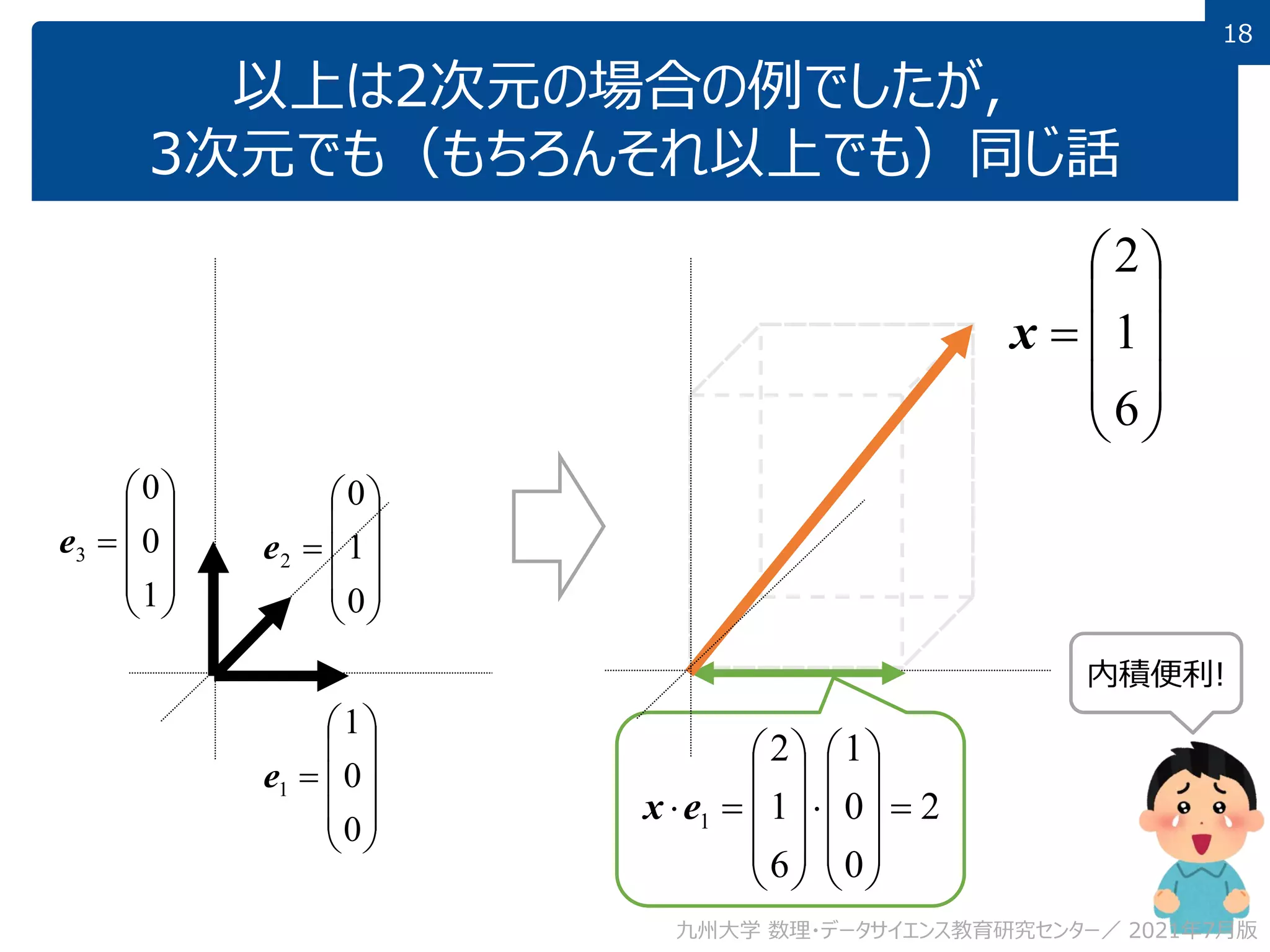
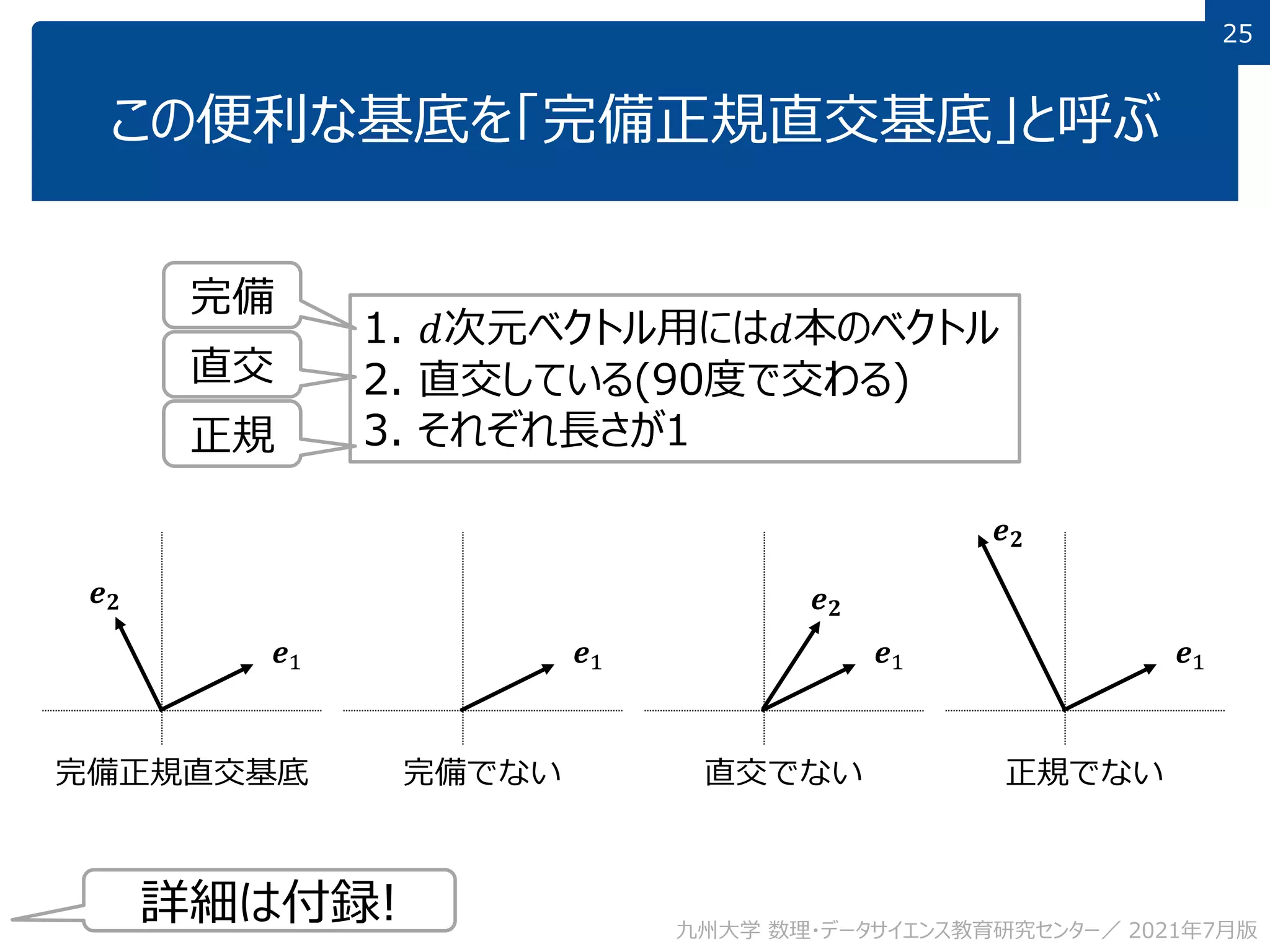
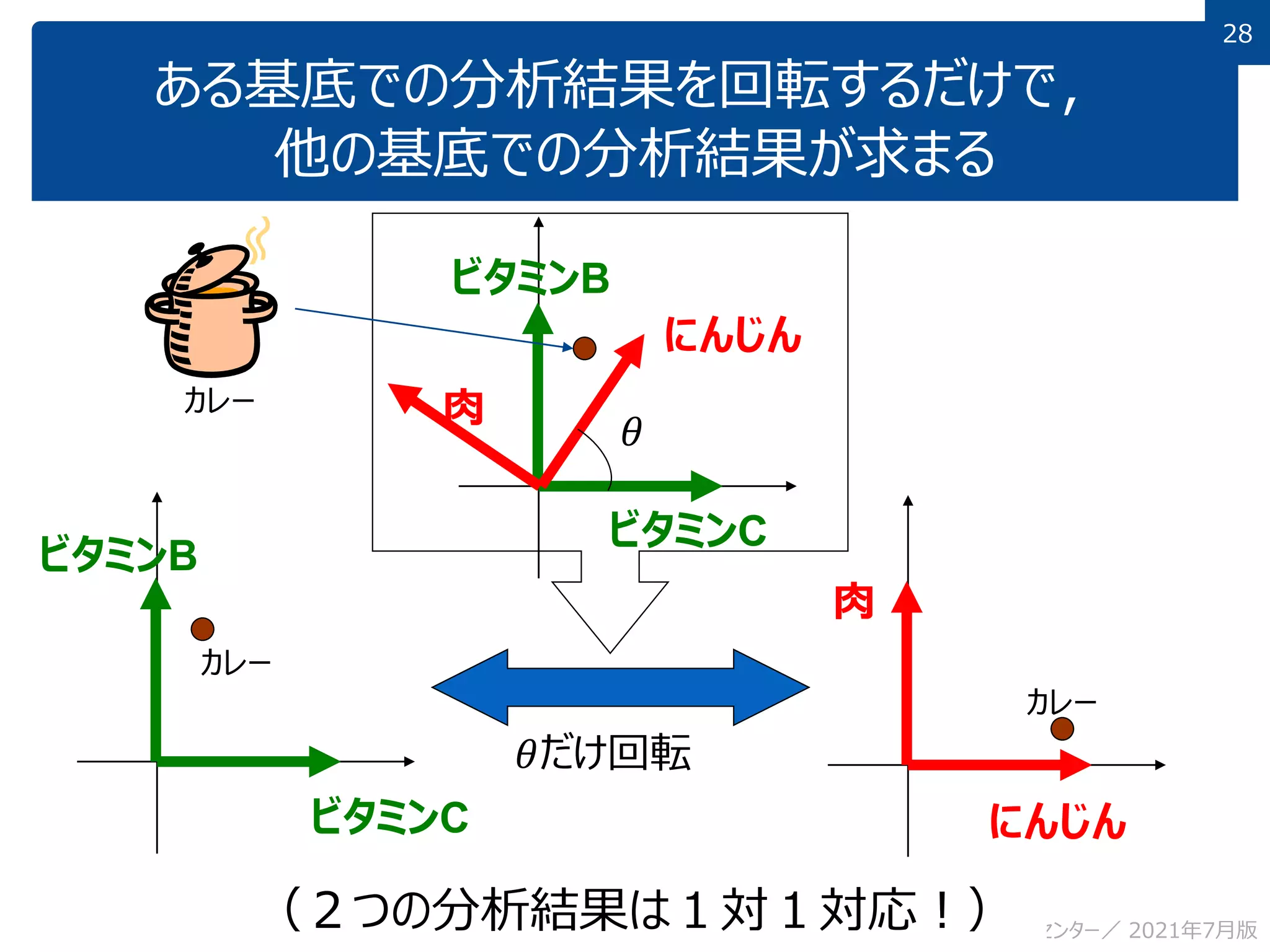
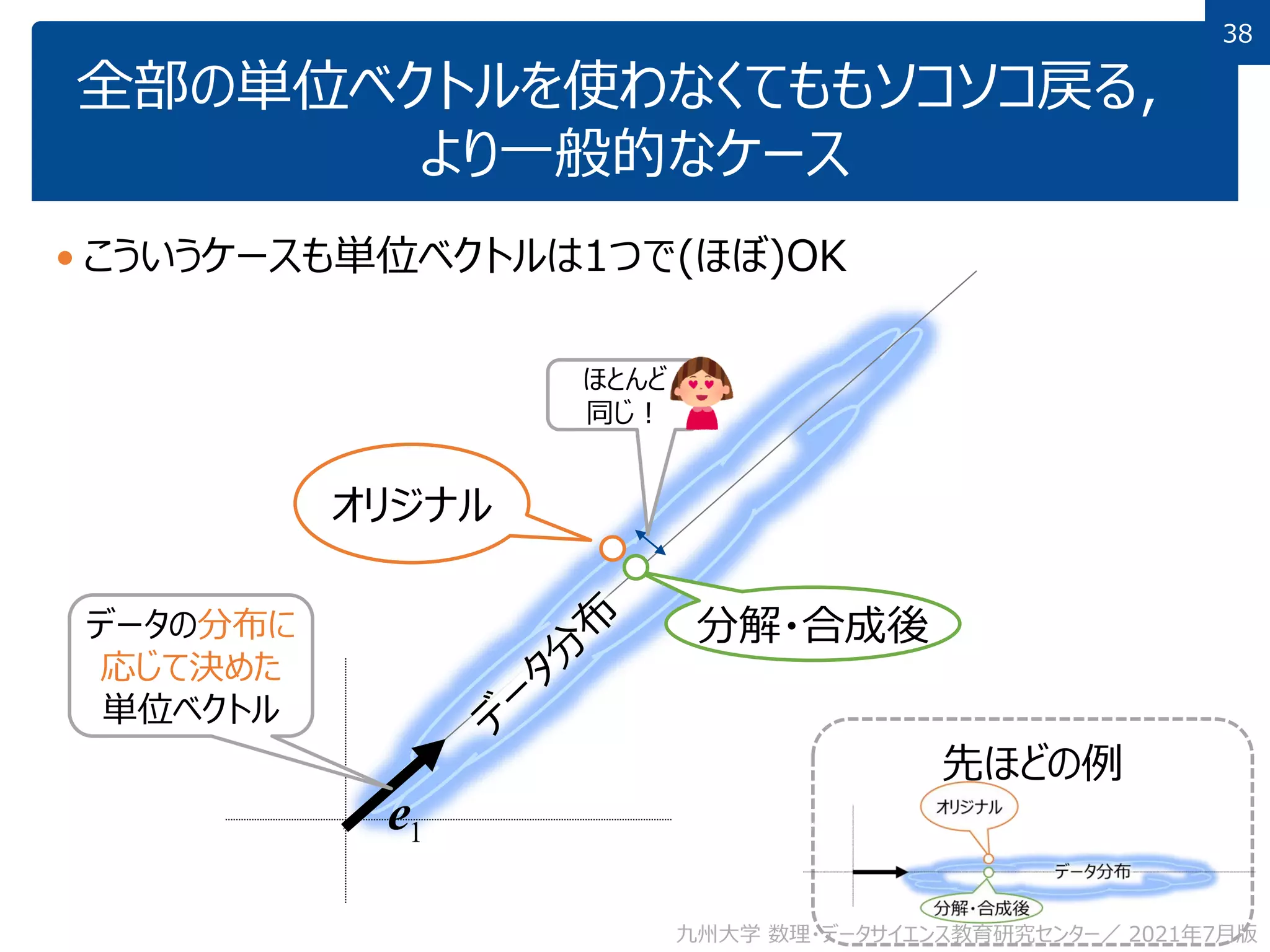
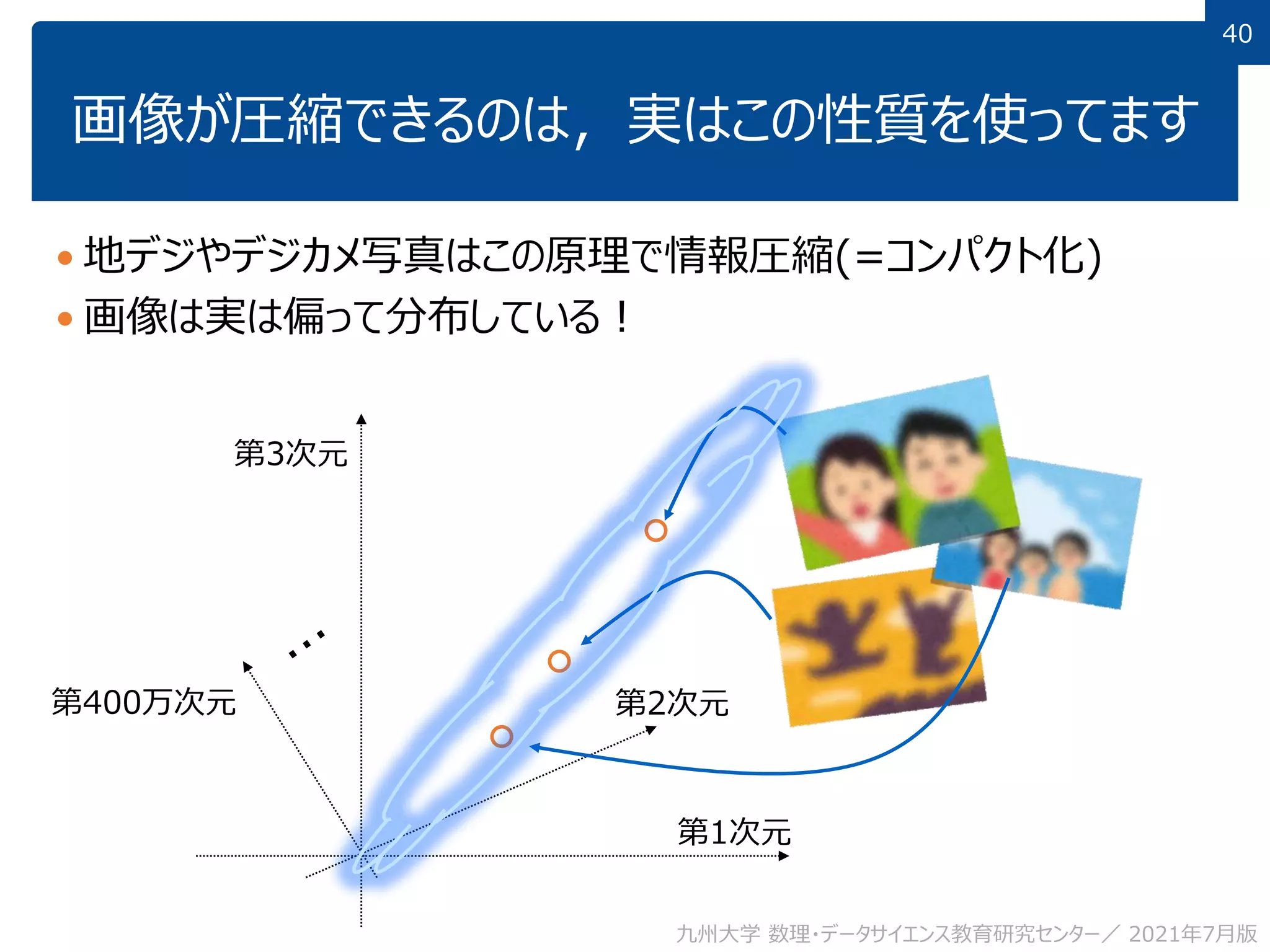
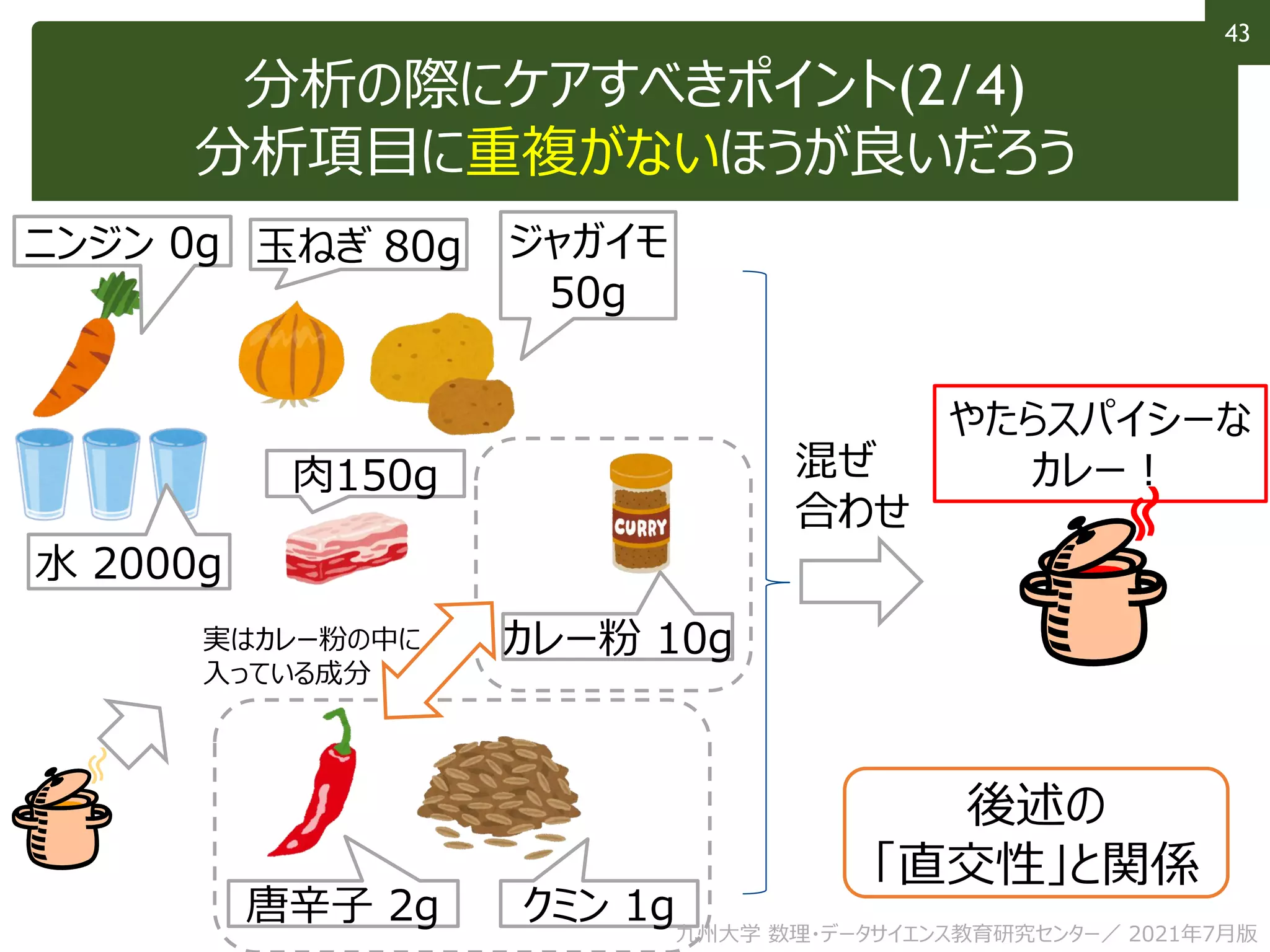
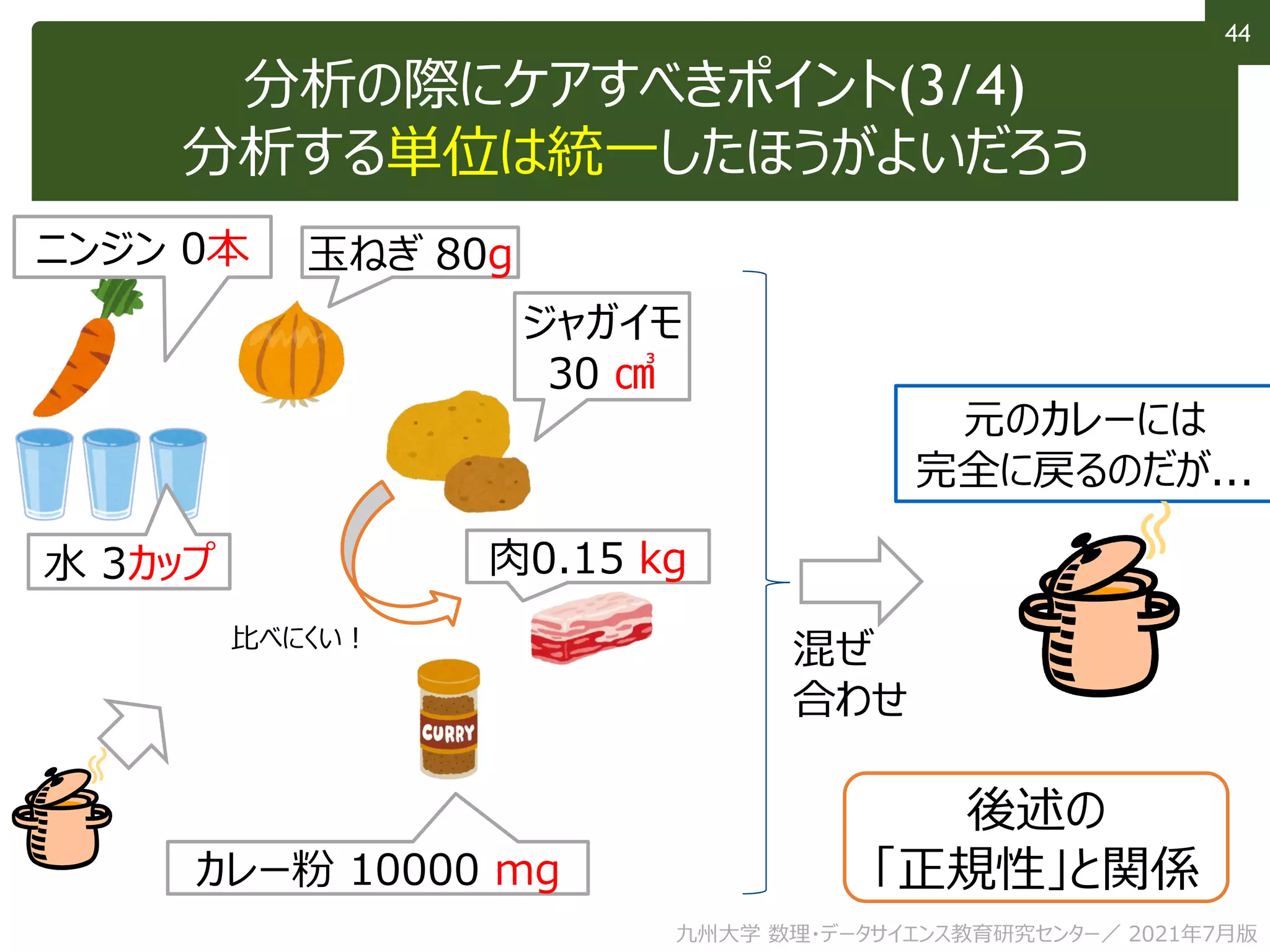
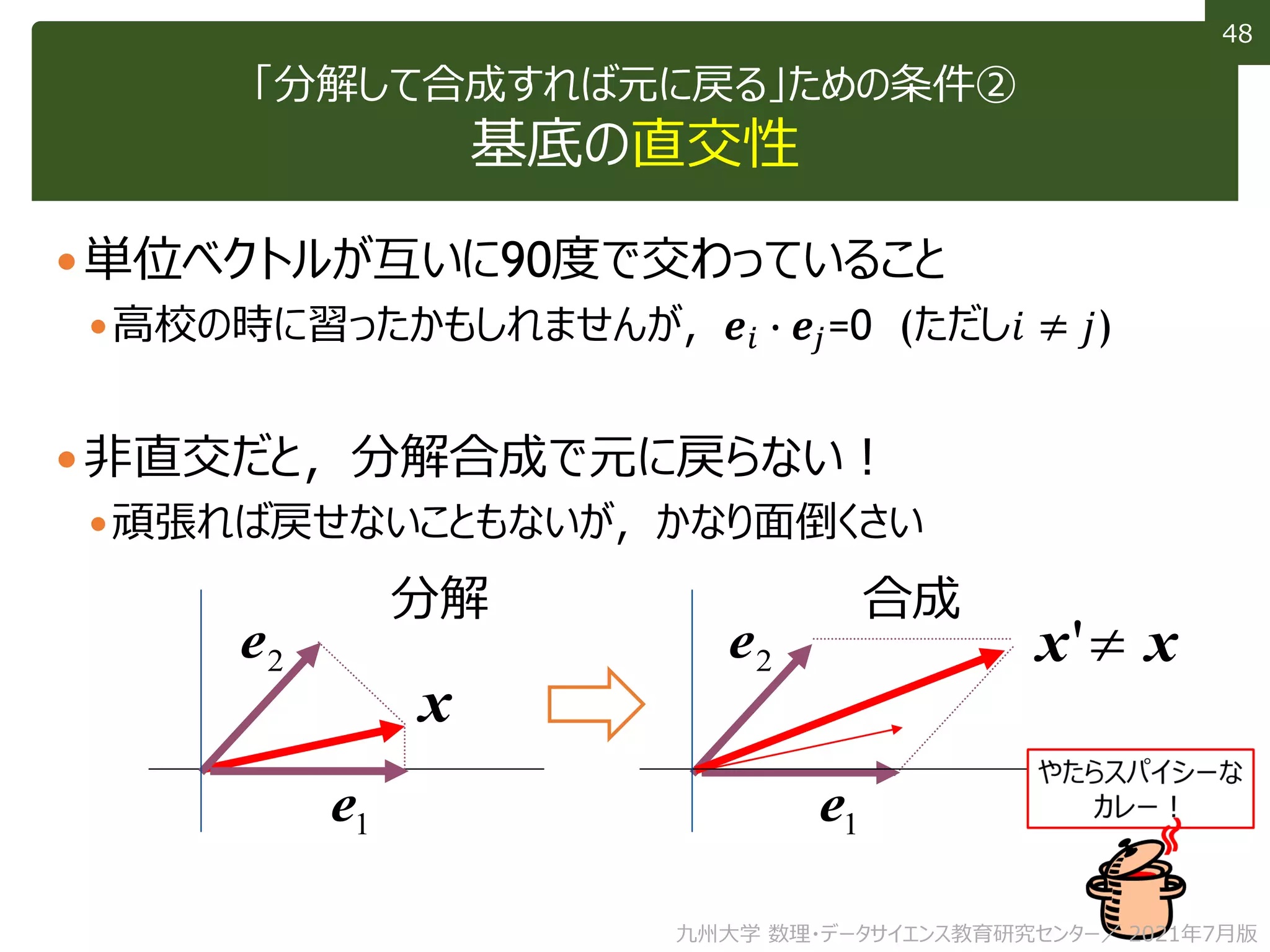
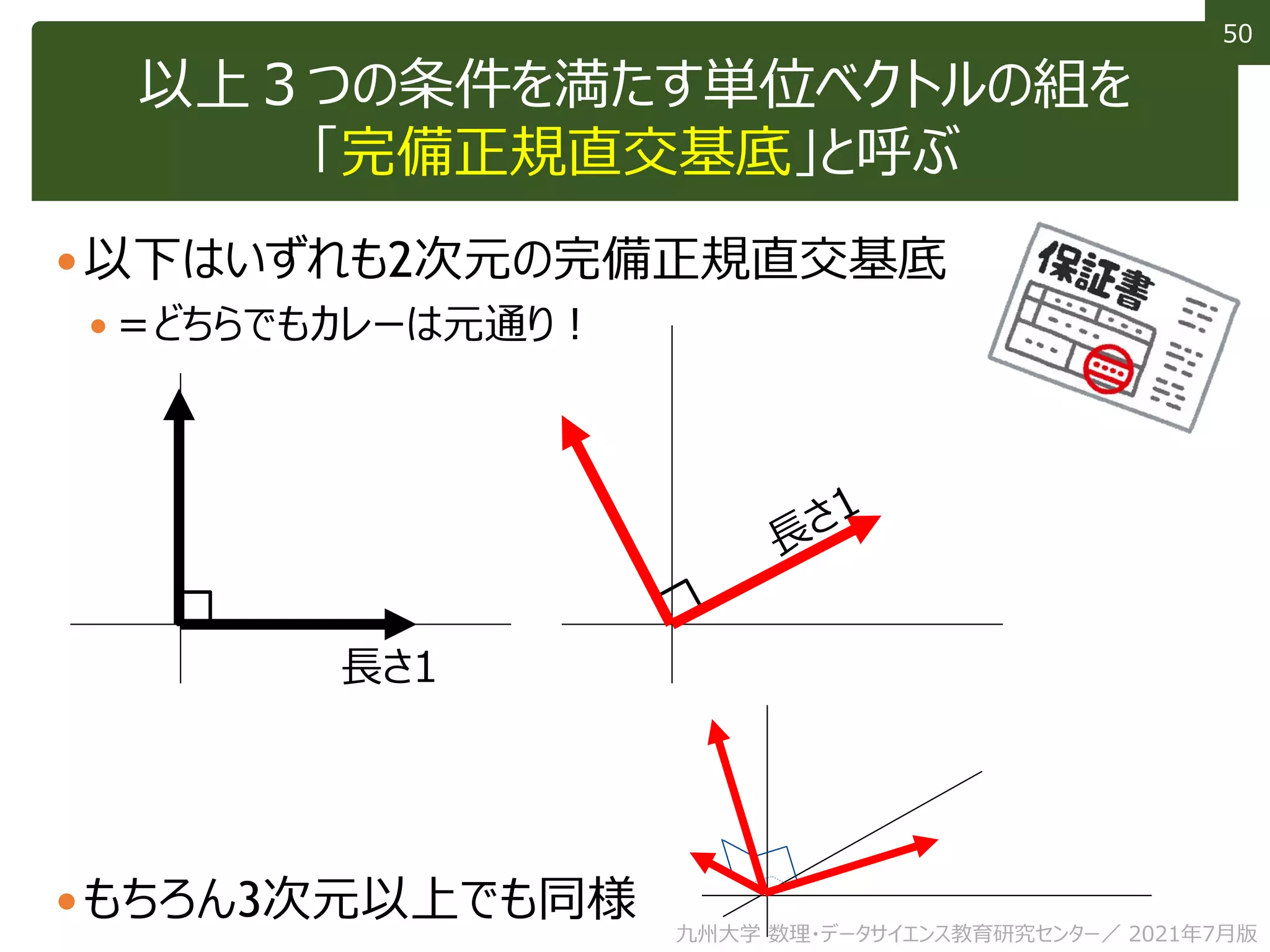
This document discusses using linear algebra concepts to analyze data. It explains that vectors can be used to represent data, with each component of the vector corresponding to a different attribute or variable. The amount of each attribute in the data is equivalent to the component value. Vectors can be decomposed into the sum of their components multiplied by basis vectors, and recomposed using those values. This relationship allows the amount of each attribute to be calculated using the inner product of the vector and basis vector. So linear algebra provides a powerful framework for understanding and analyzing complex, multi-dimensional data.