CB
Uploaded byChristophe Bontemps
409 views

Meetup Maps & Networks: Why and How to visualize

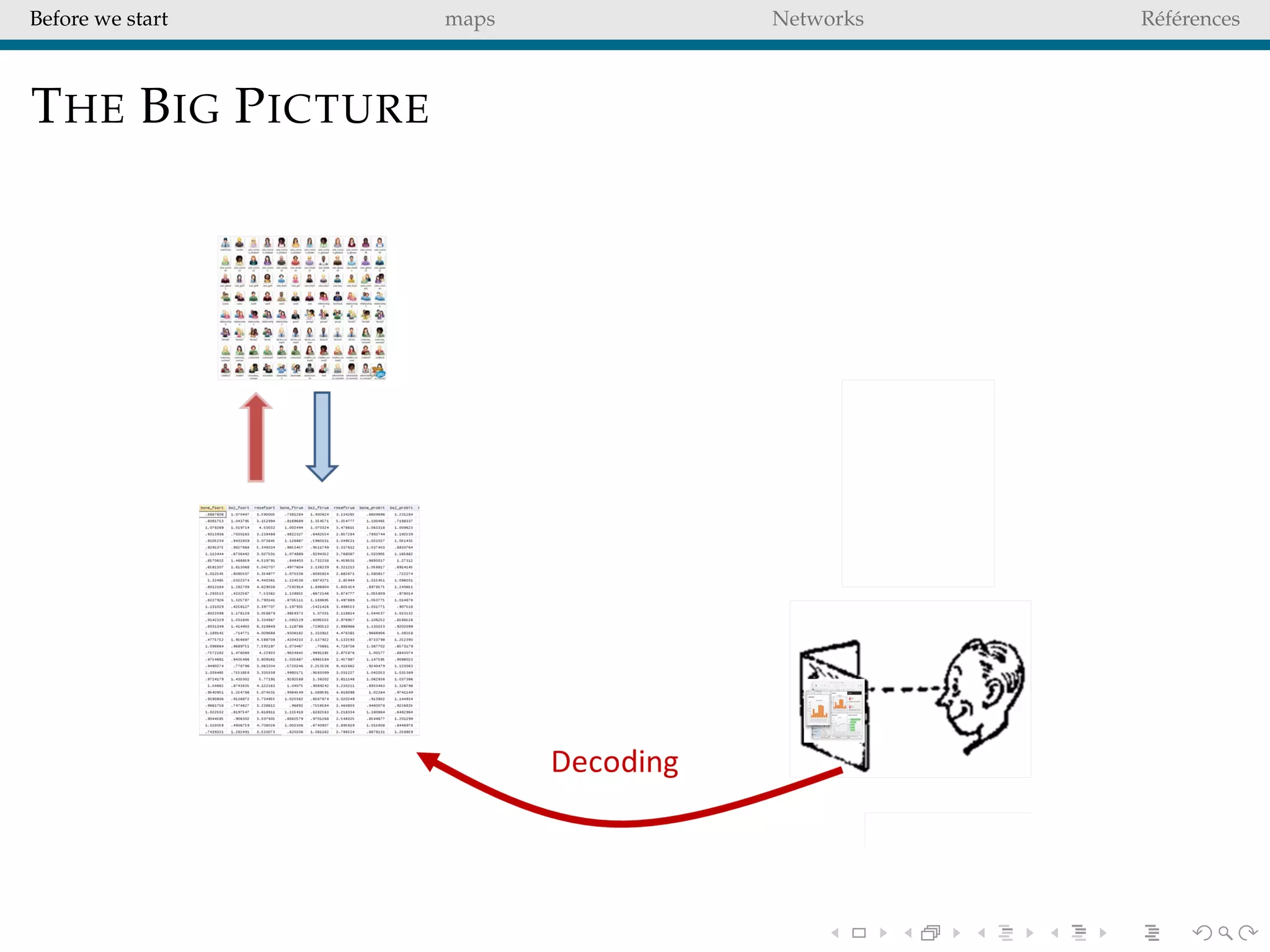
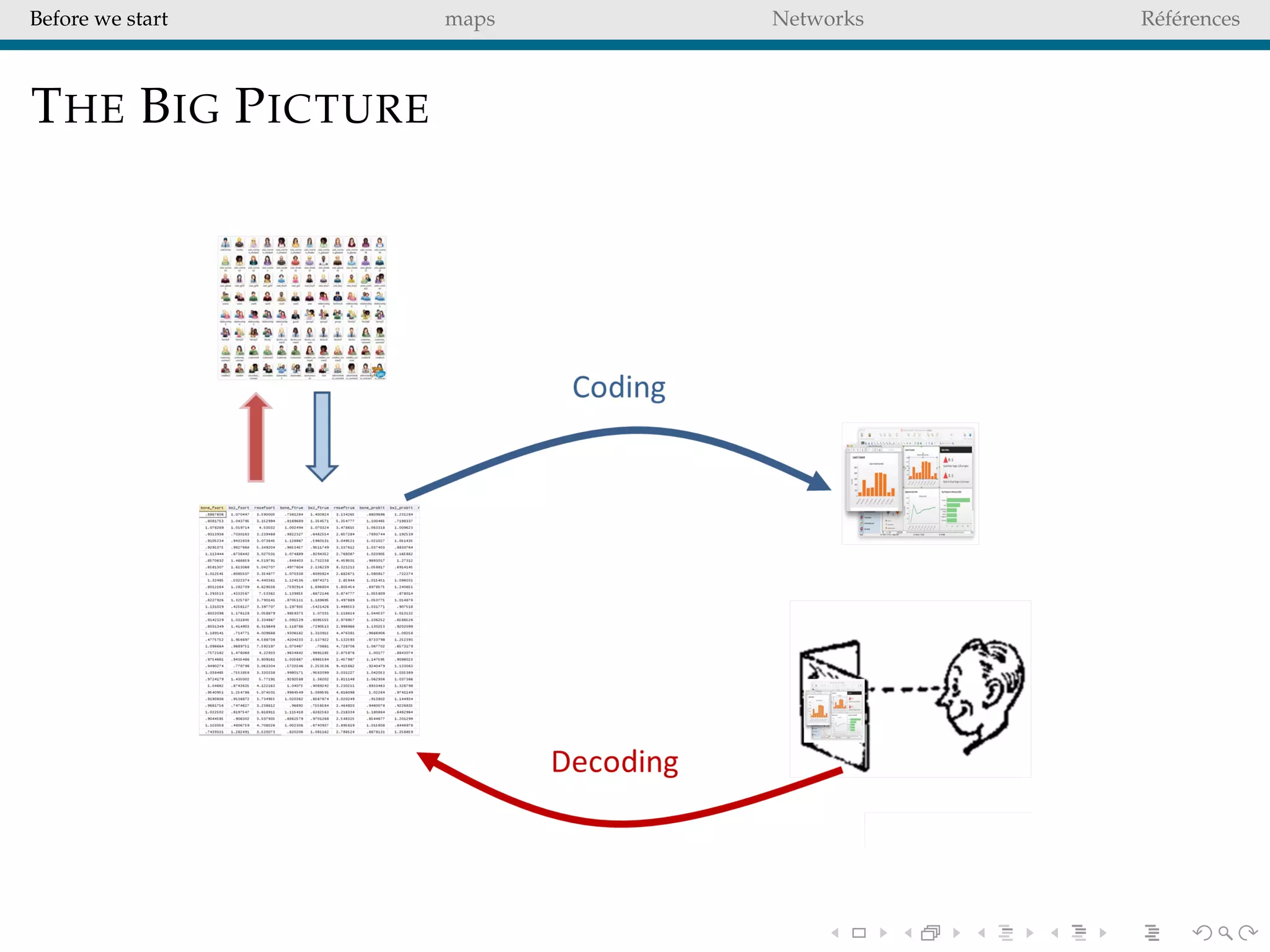
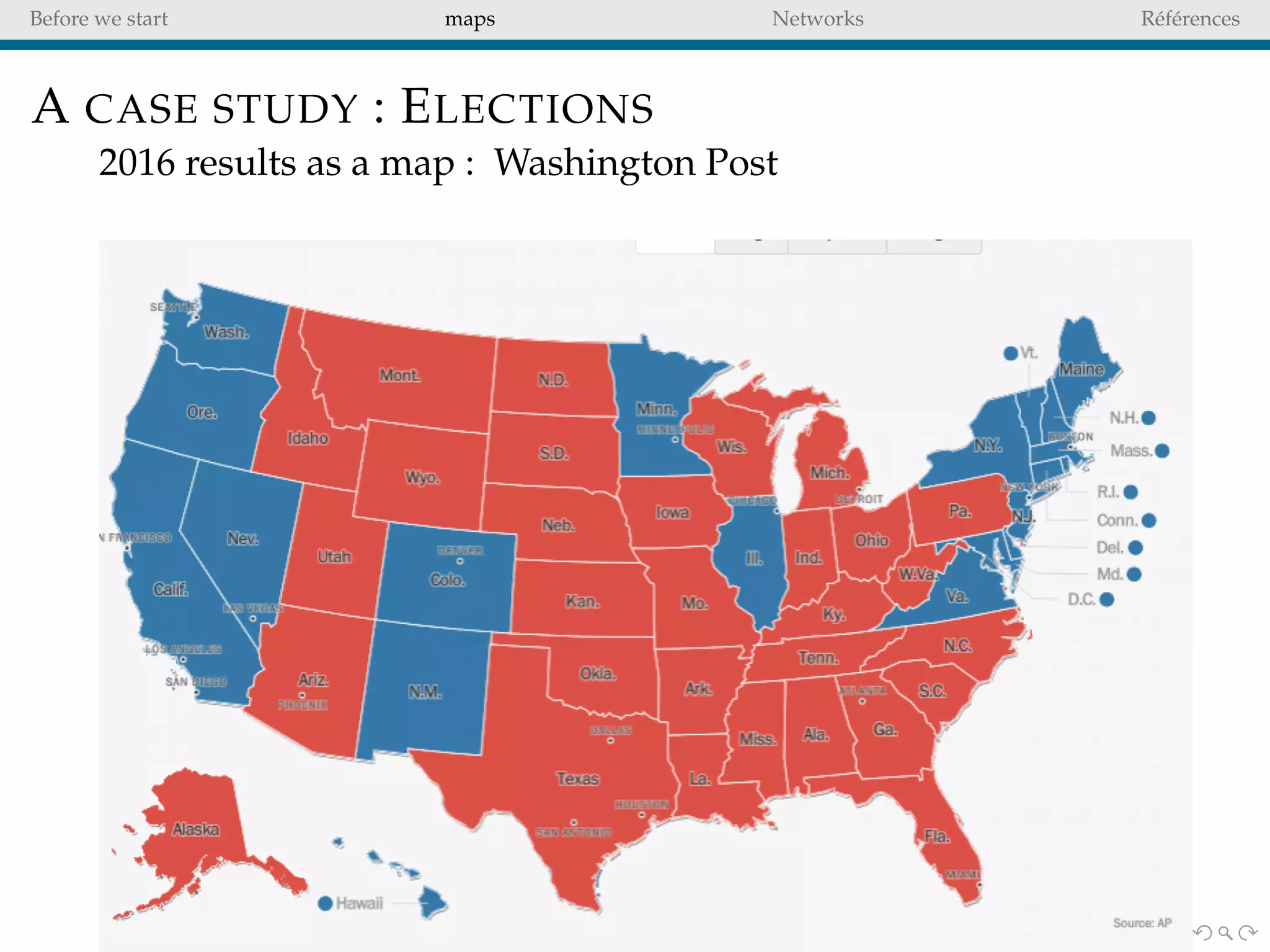
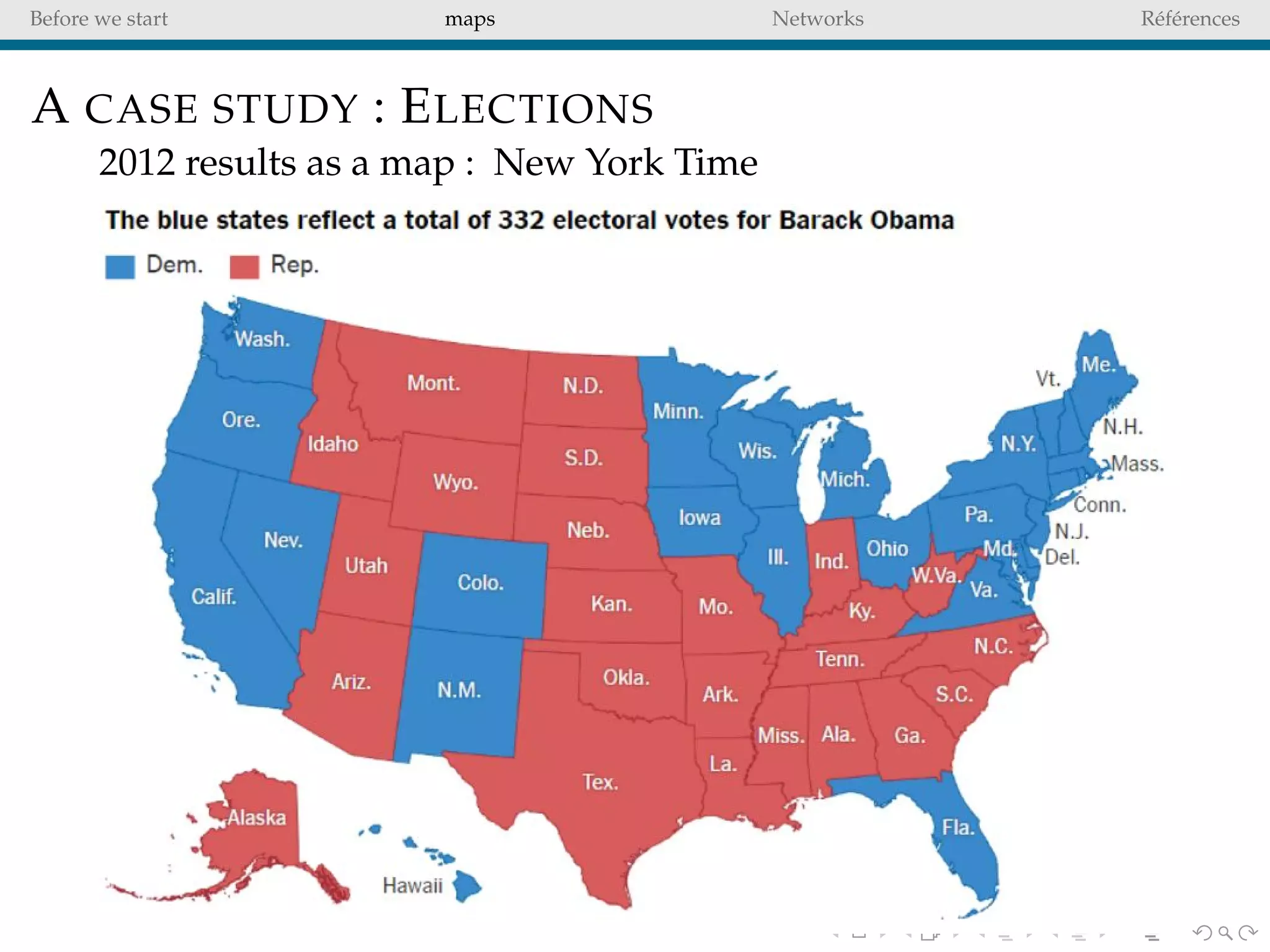
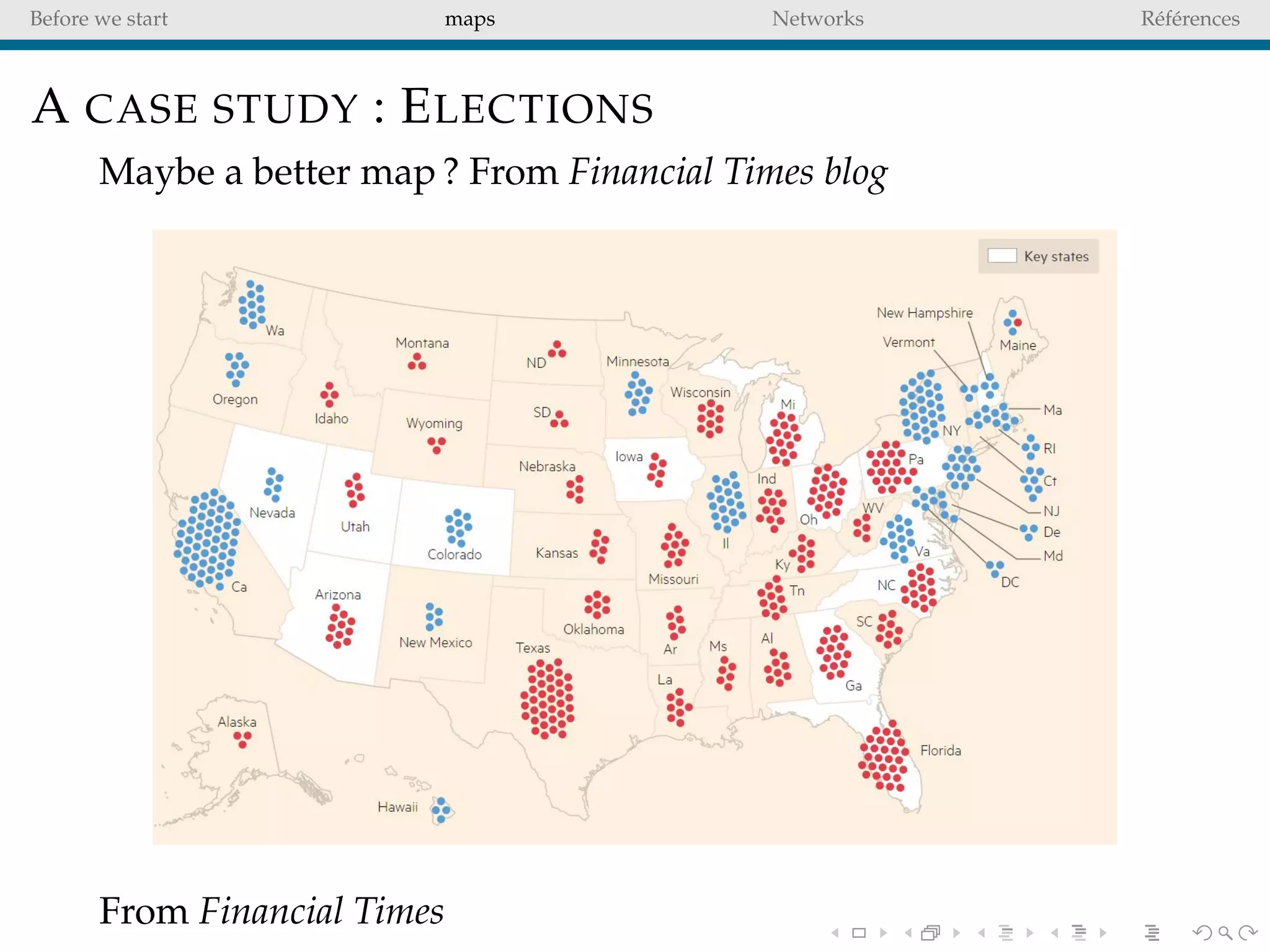
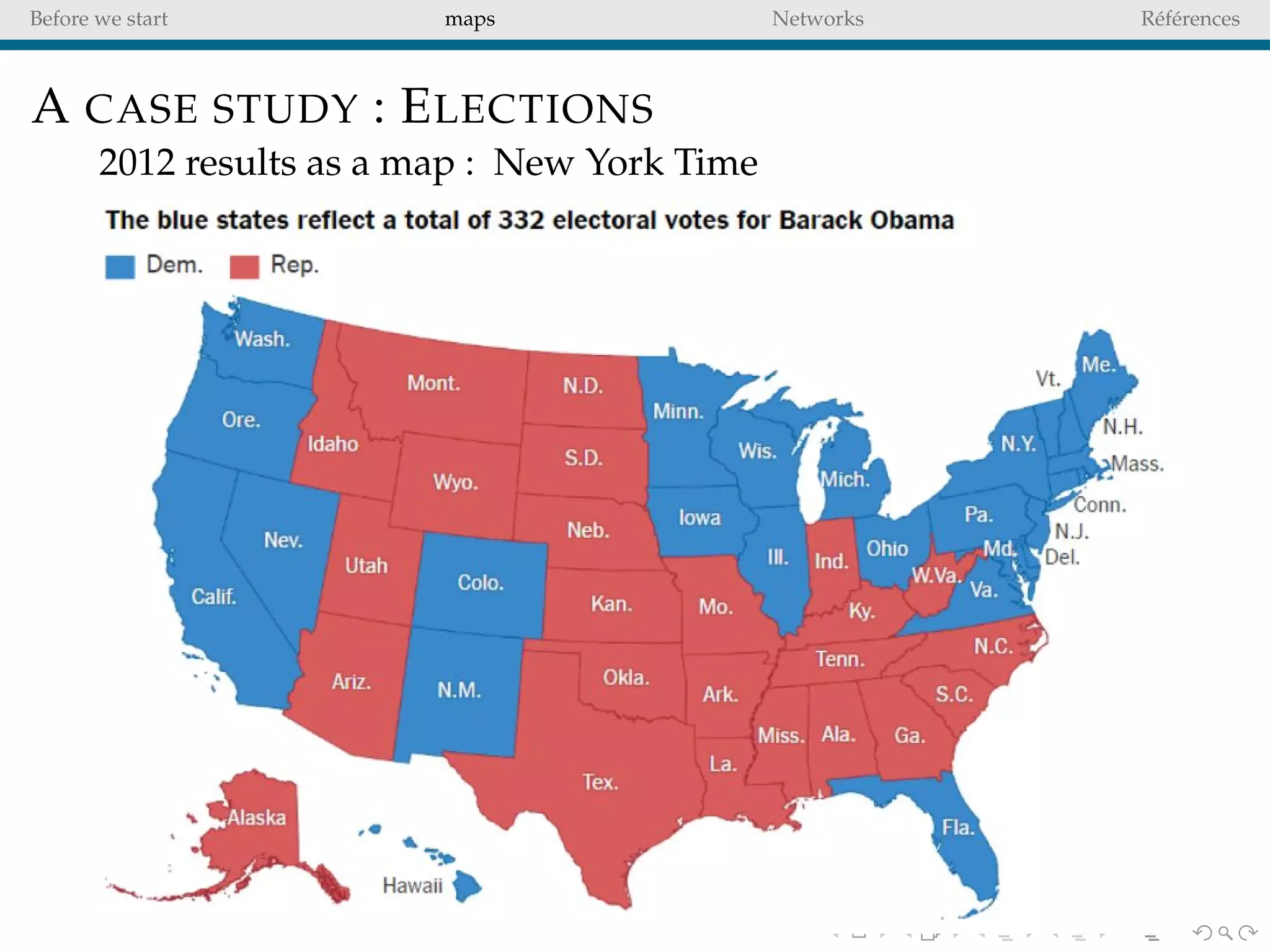
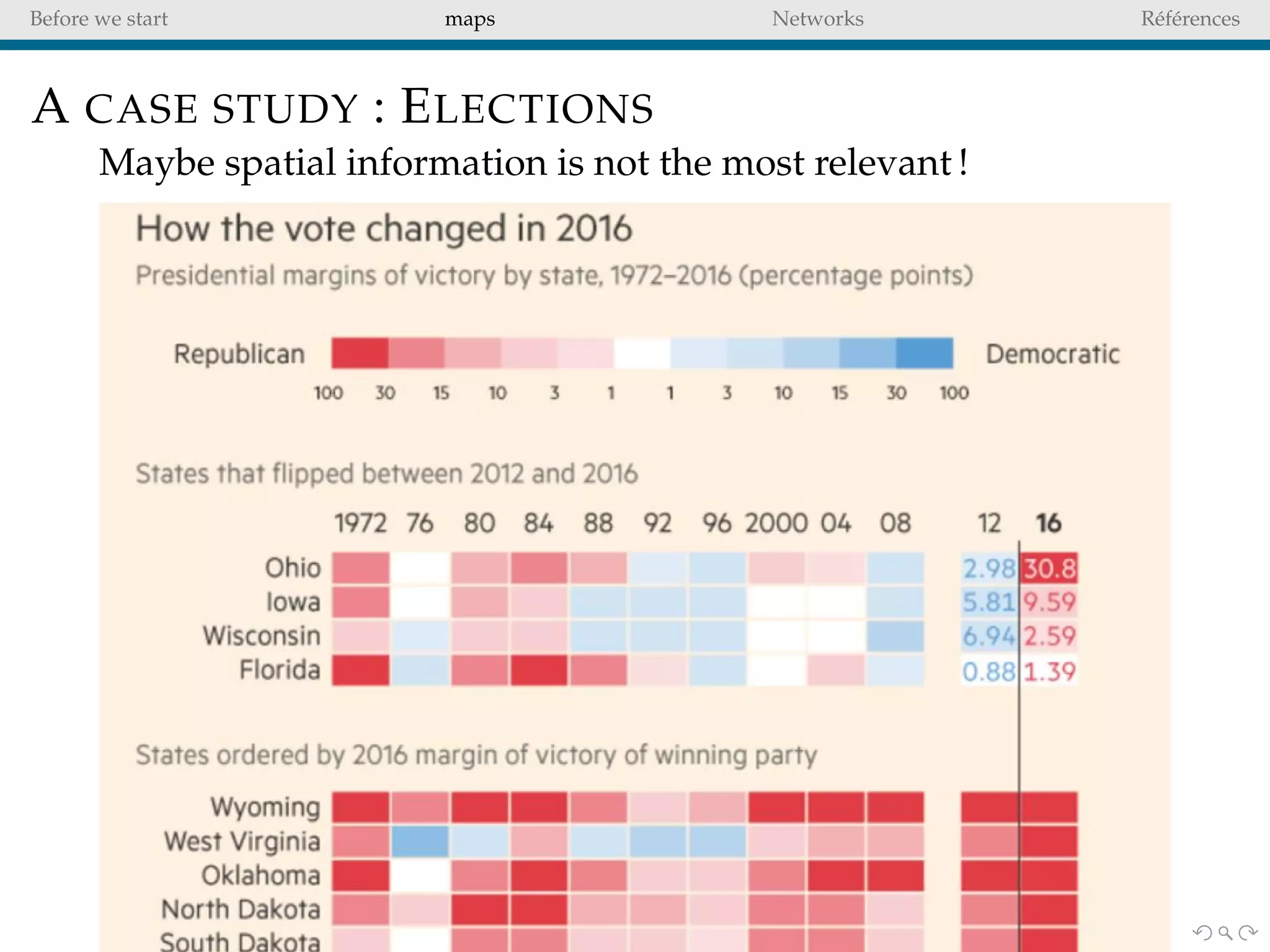
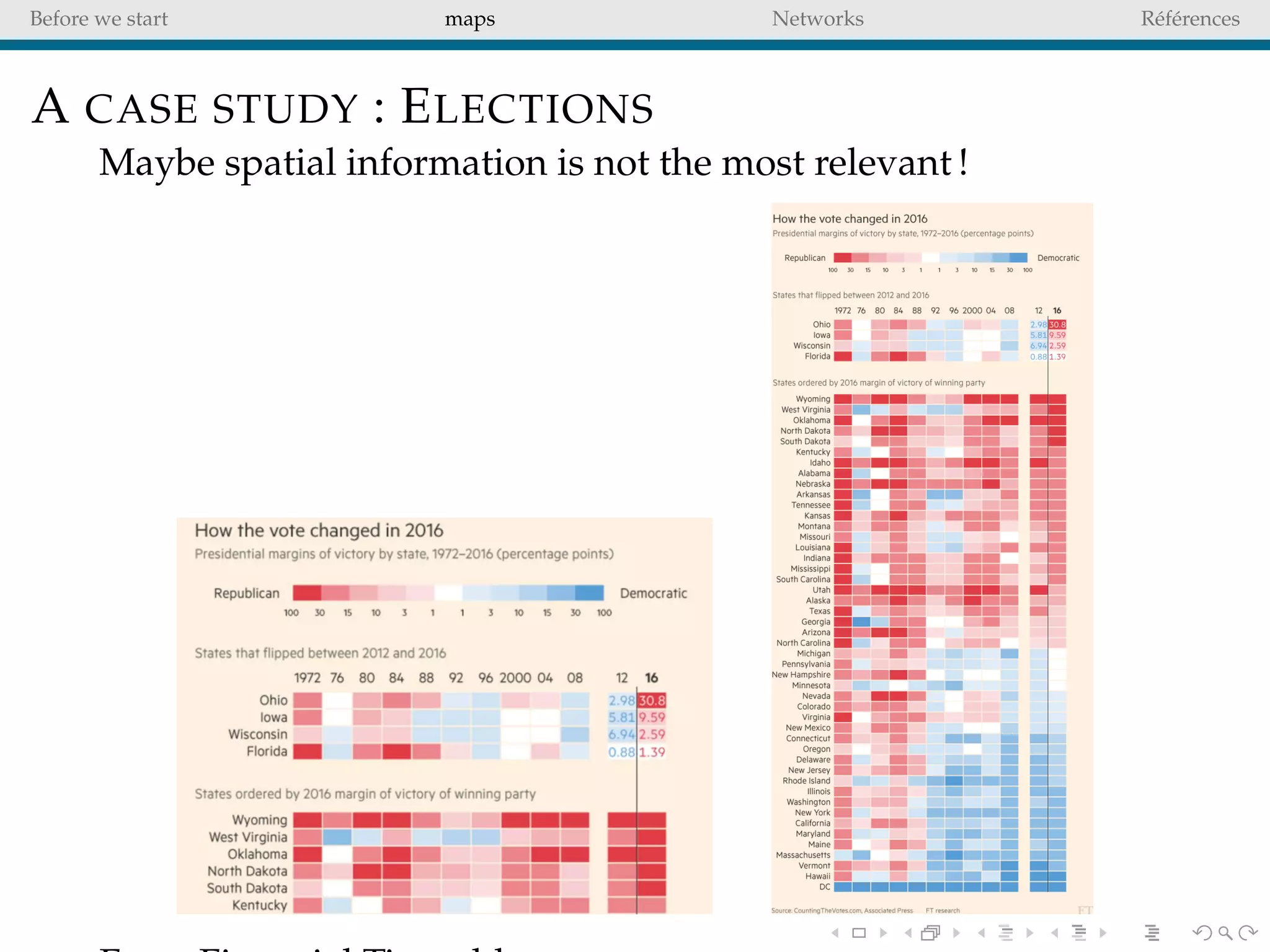
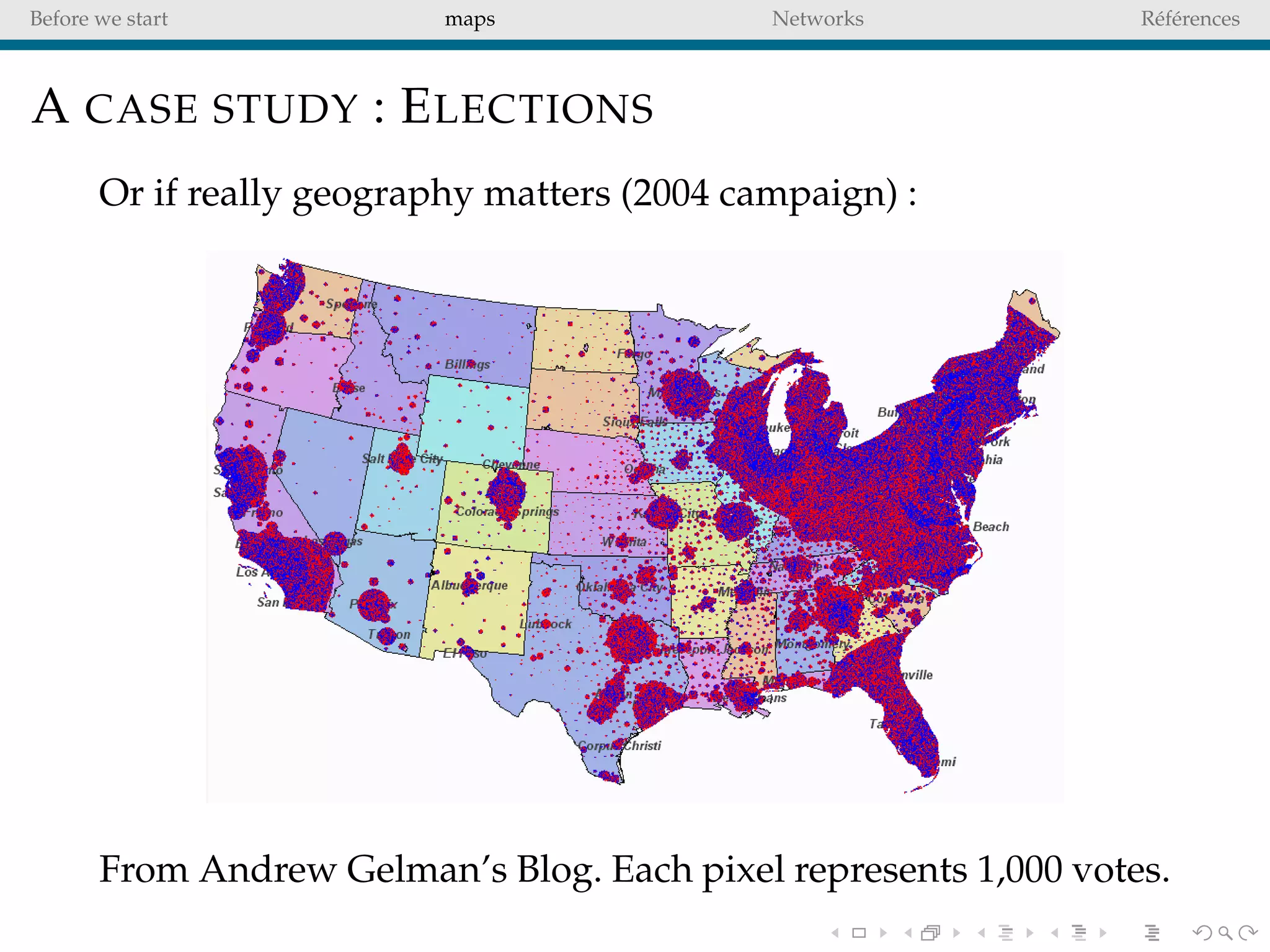
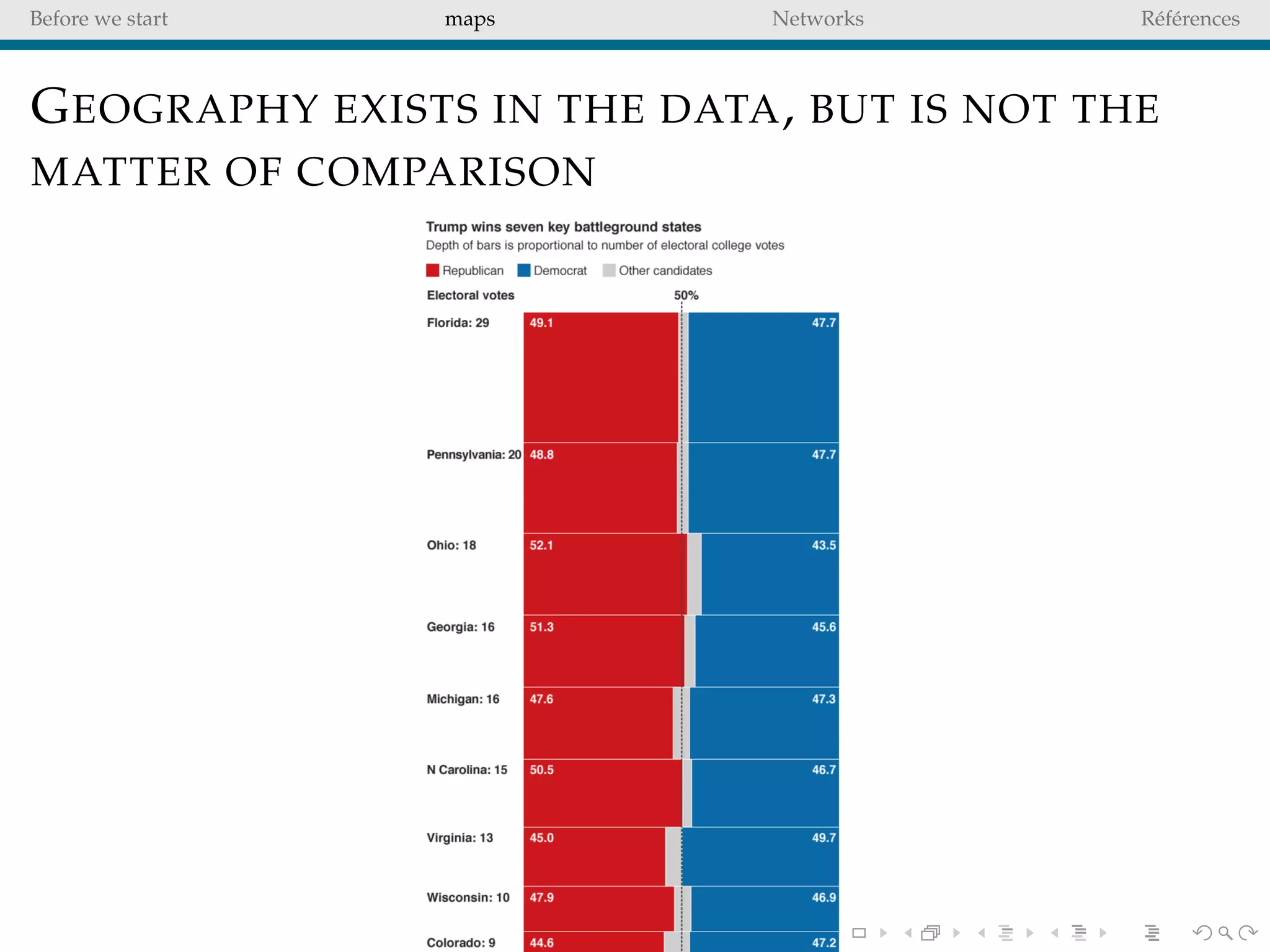
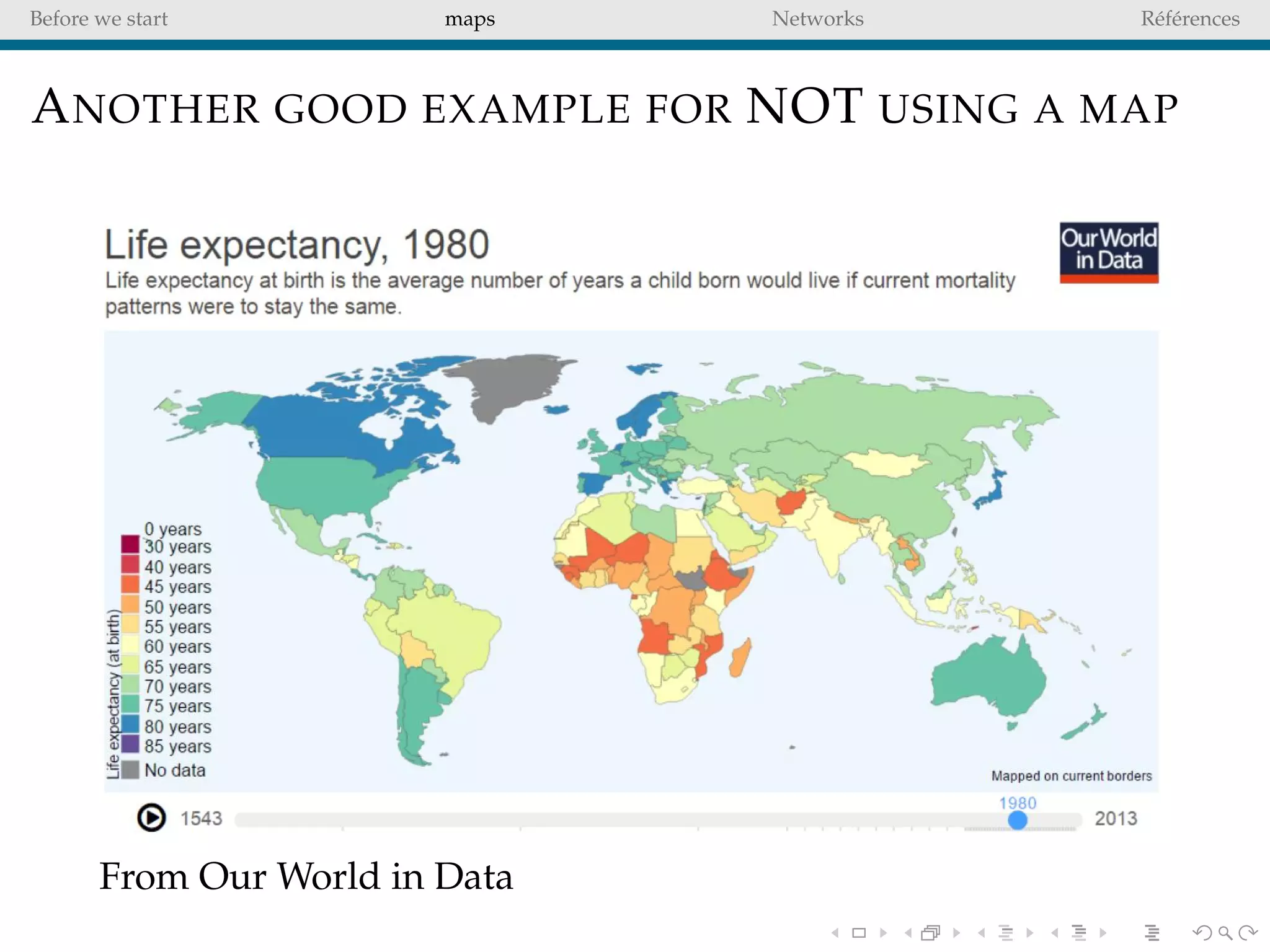
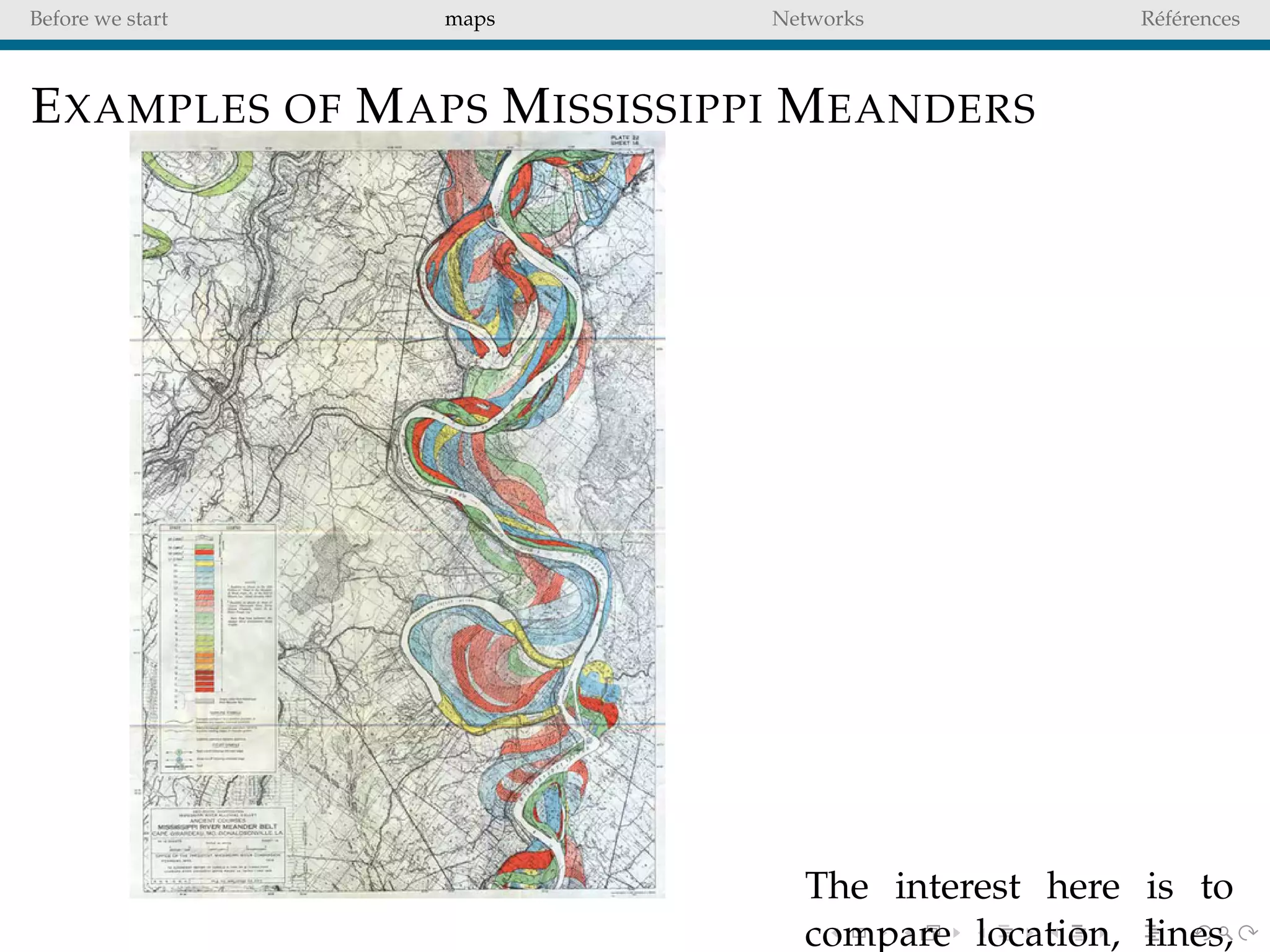
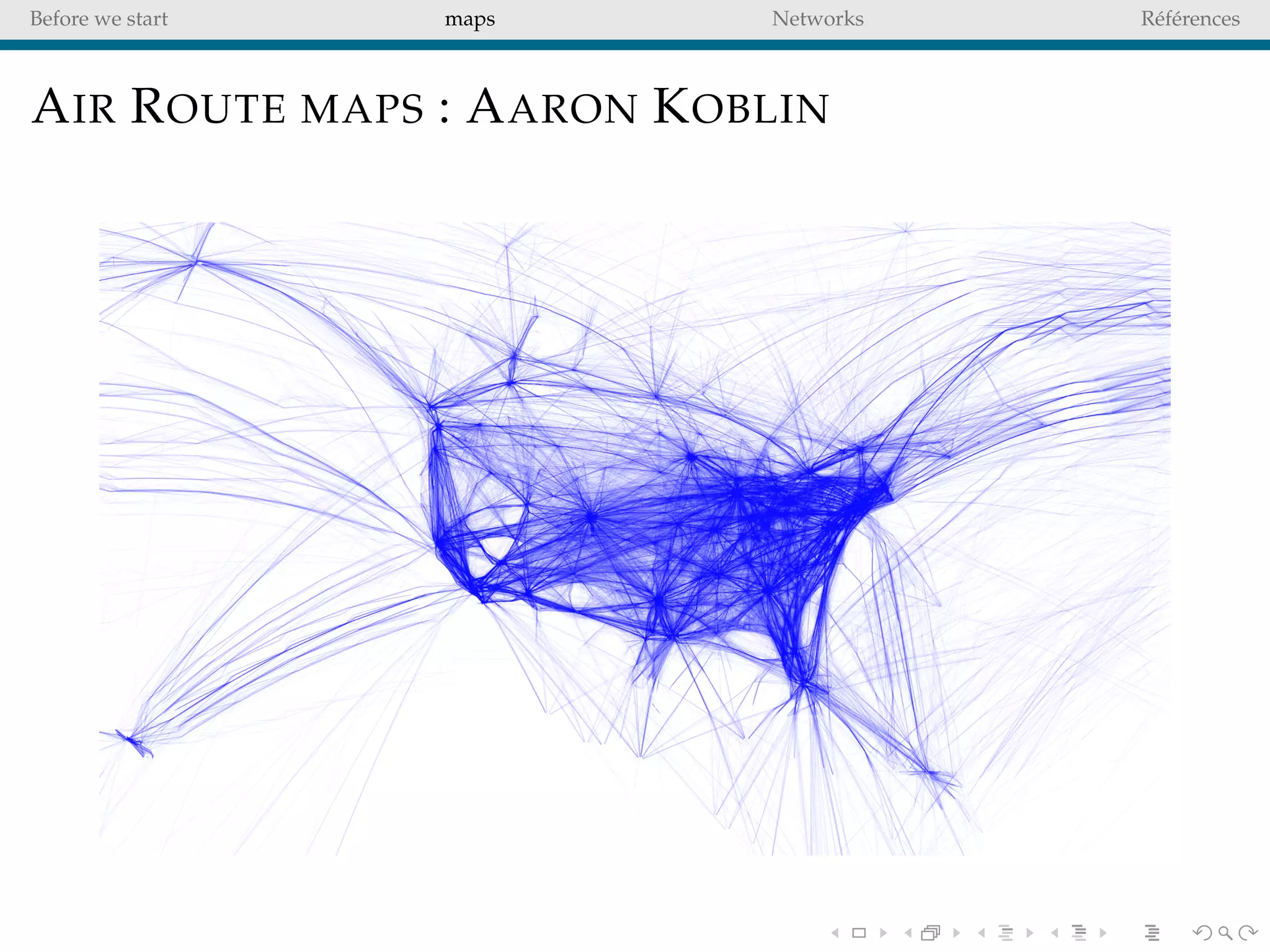
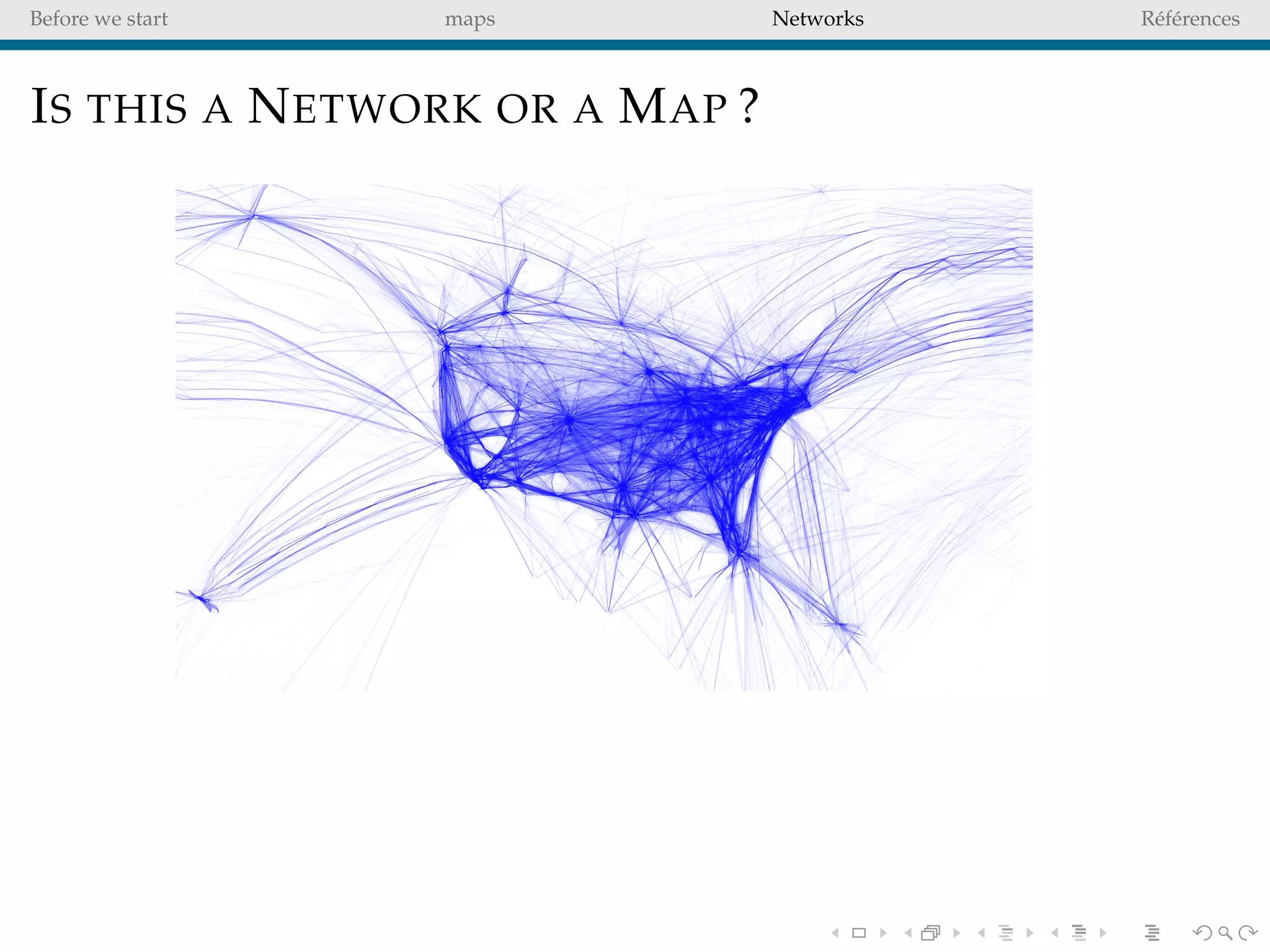
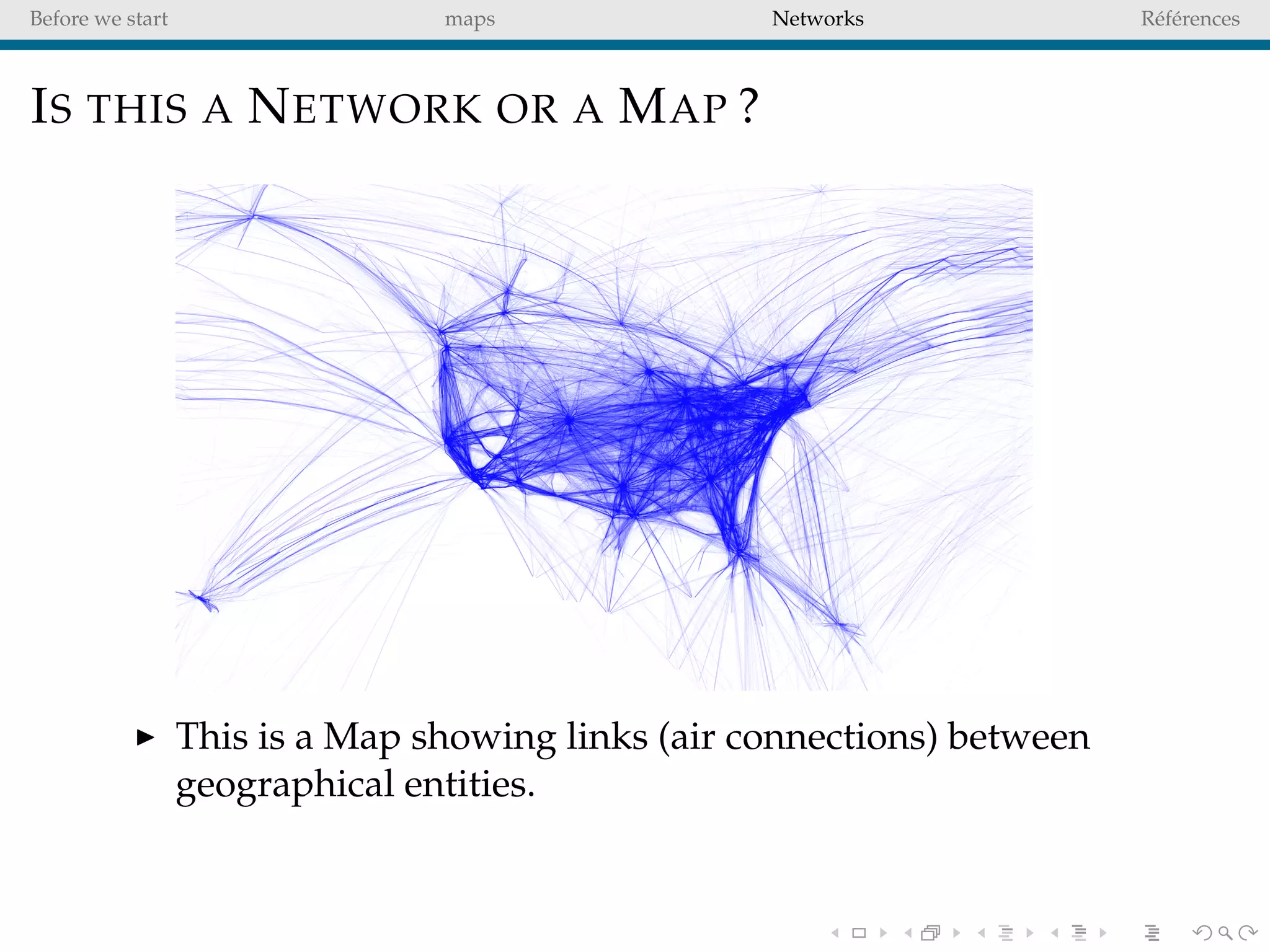
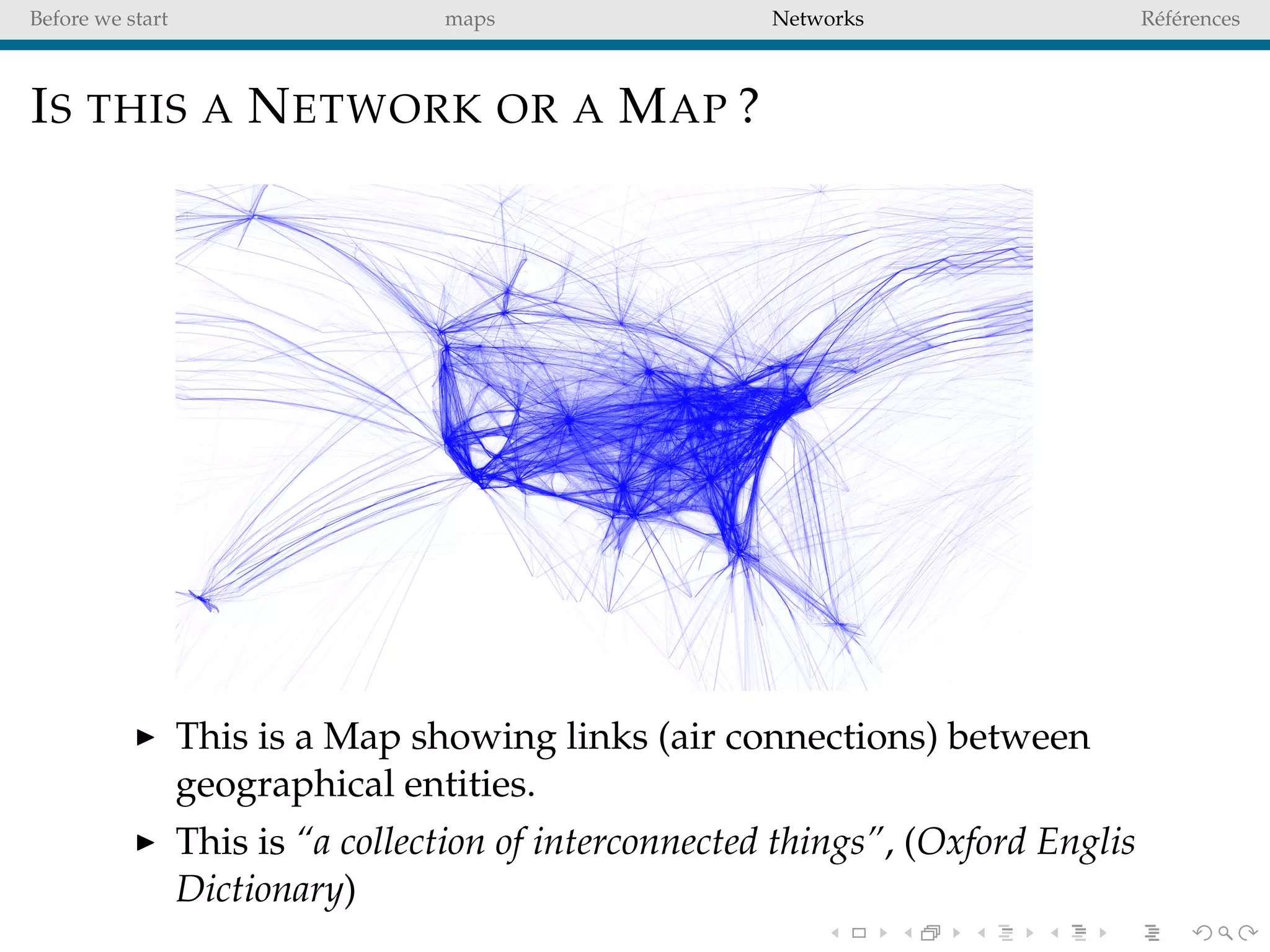
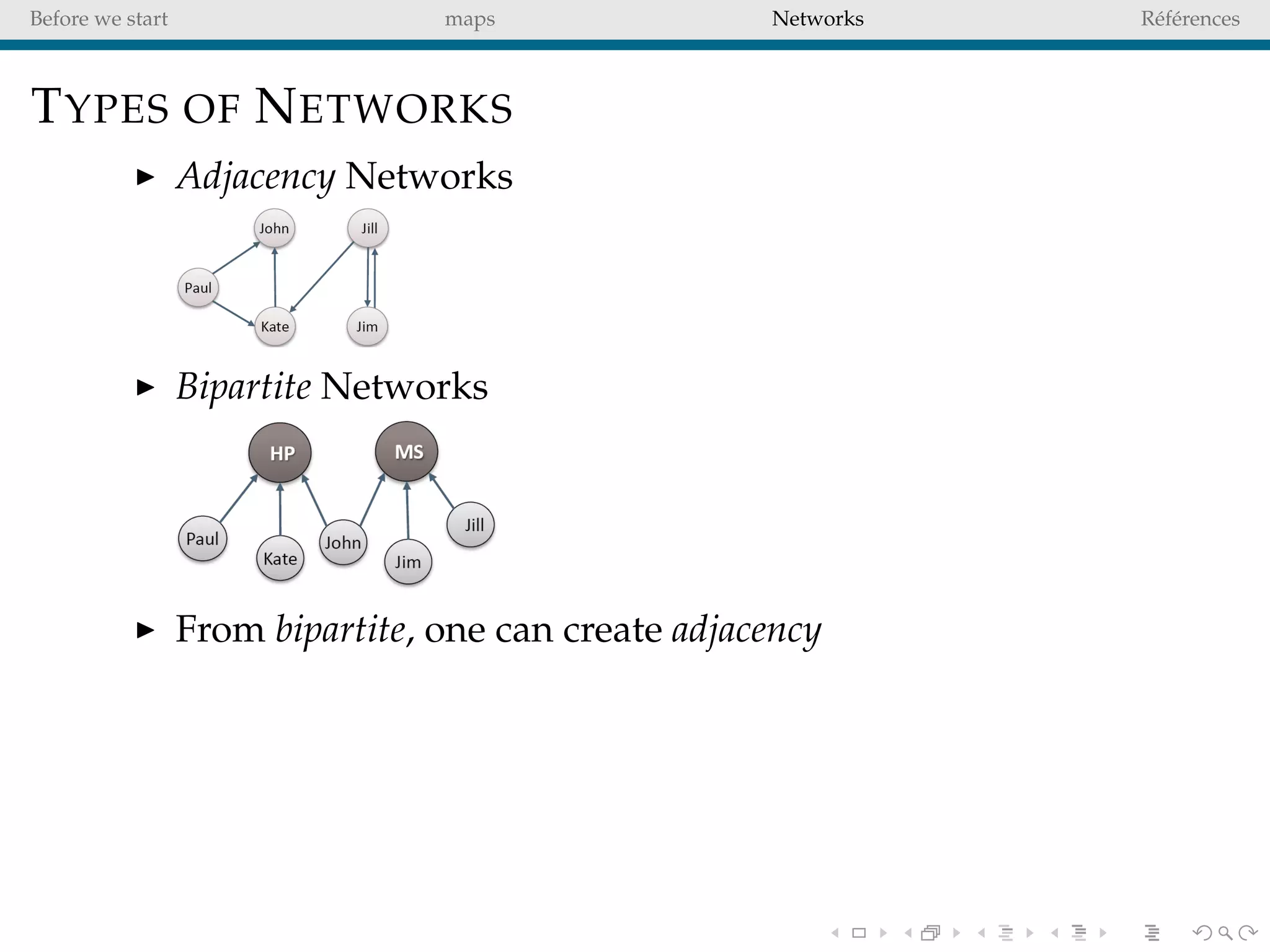
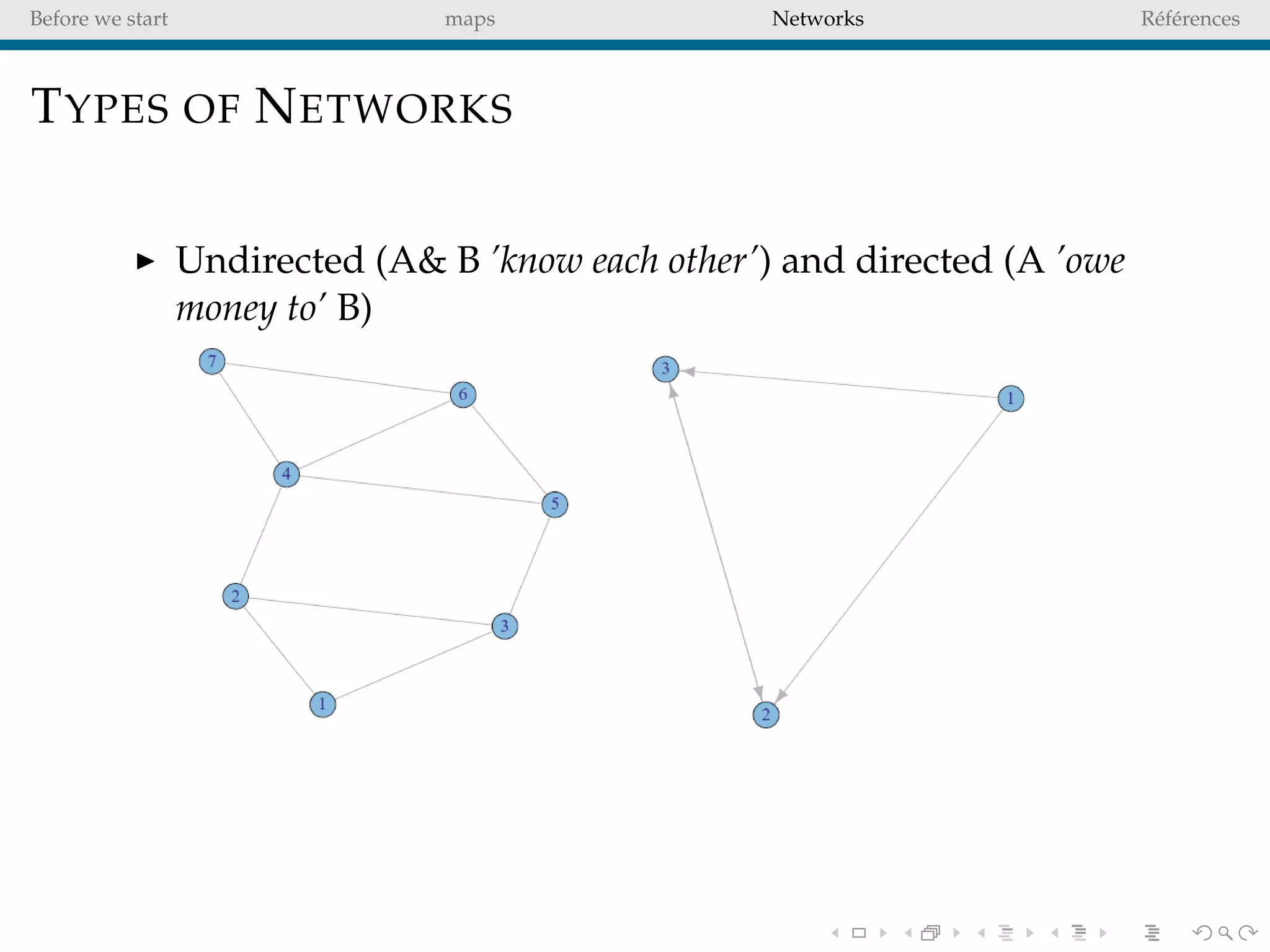
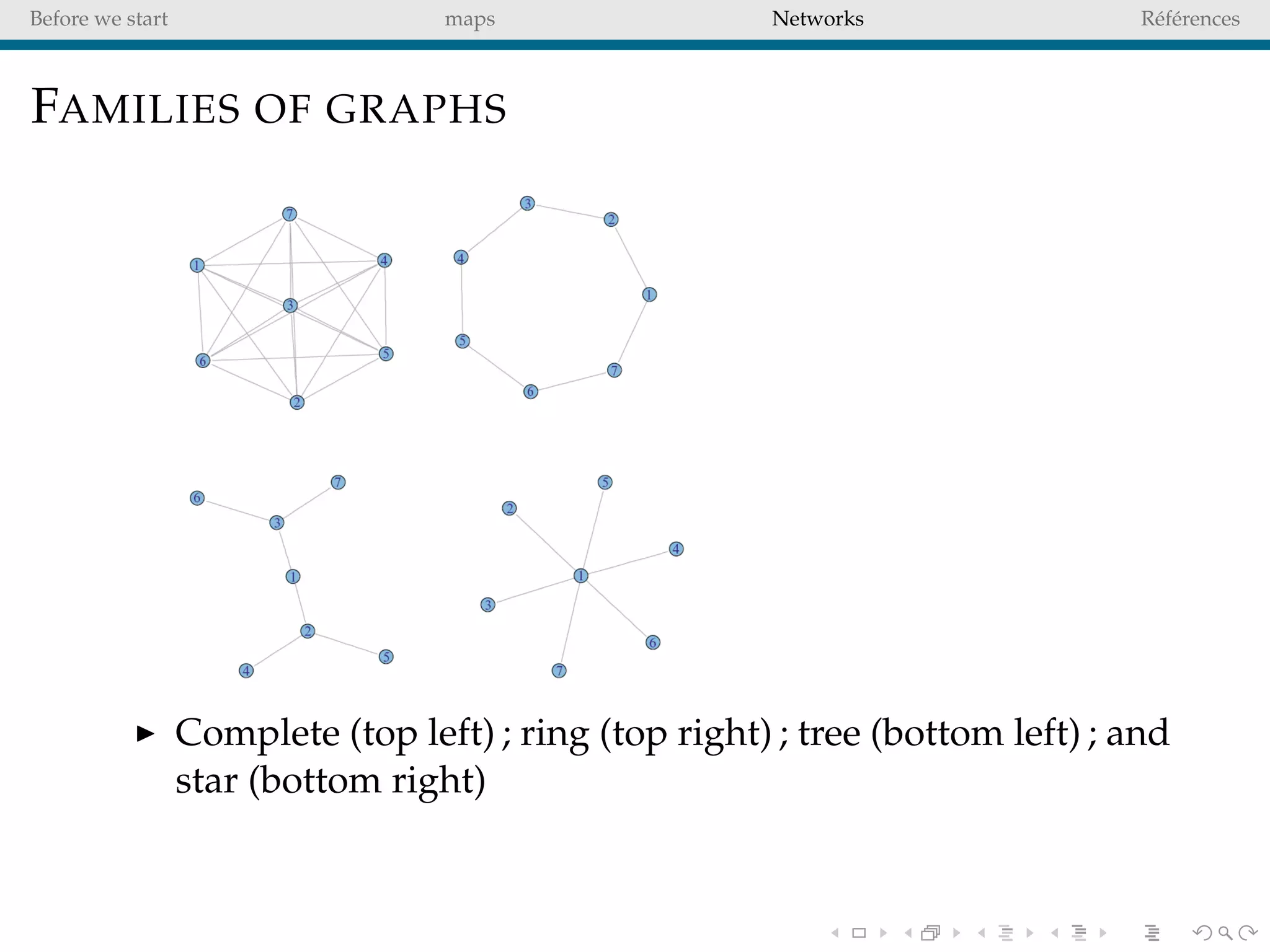
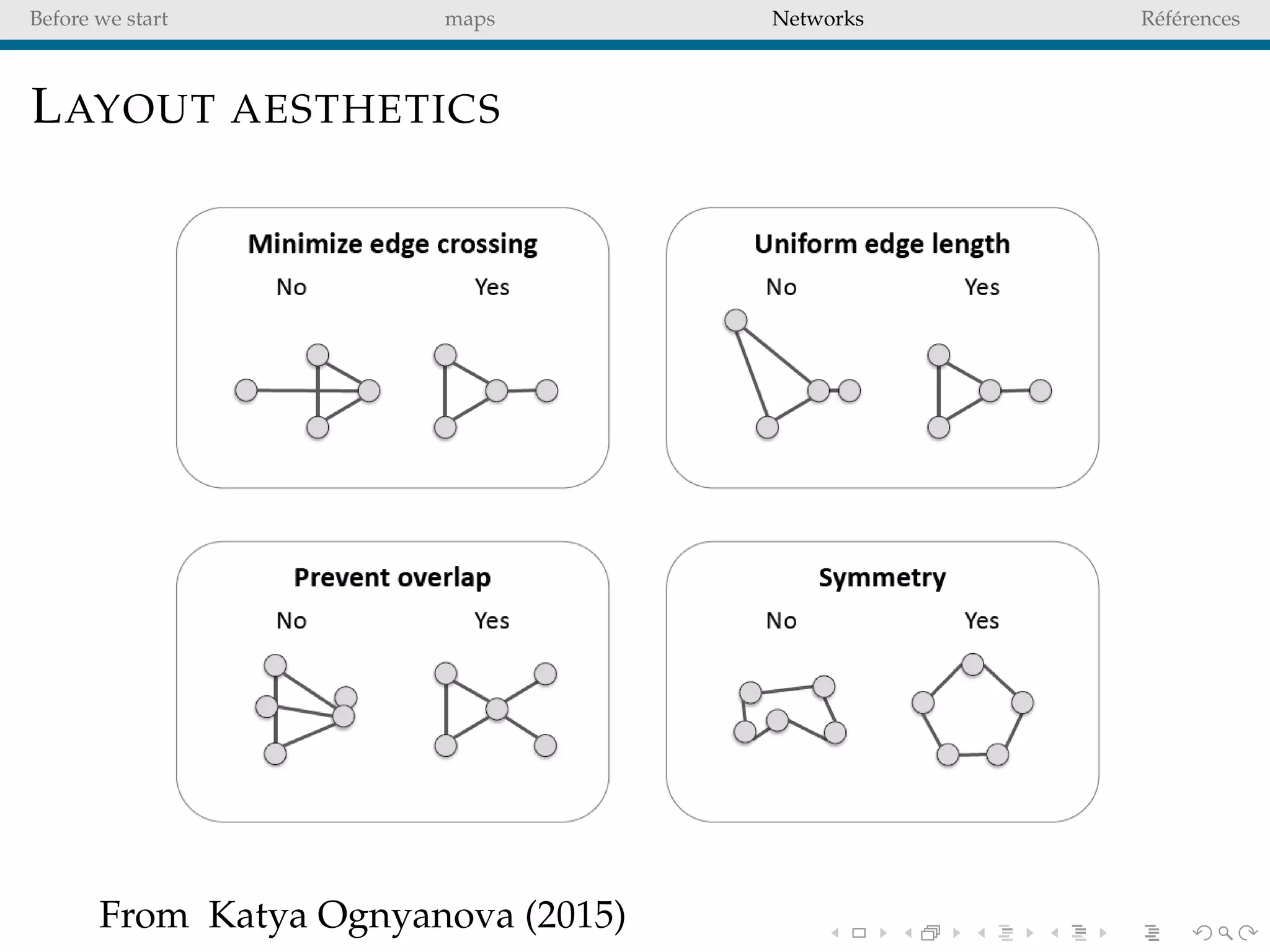
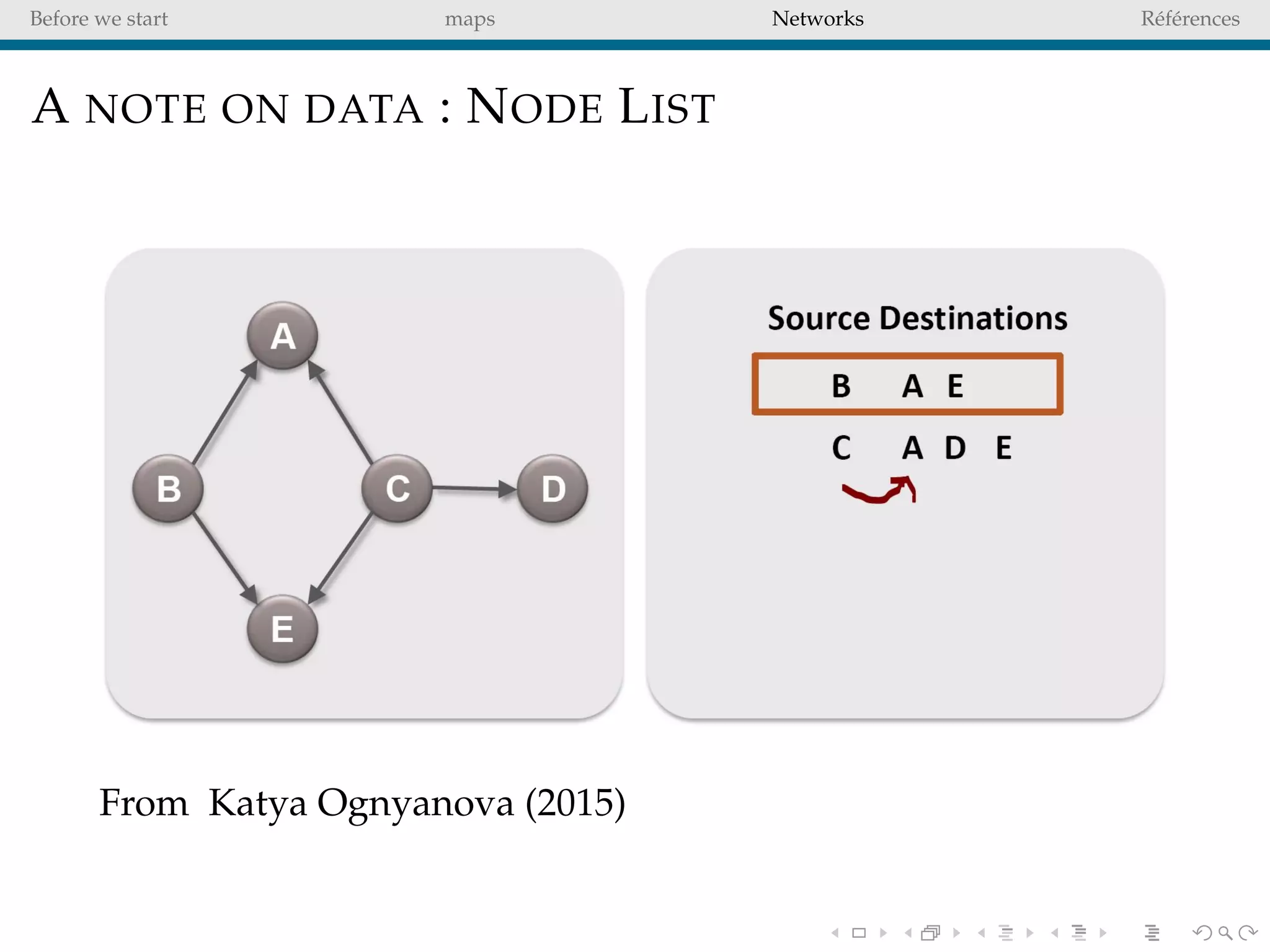
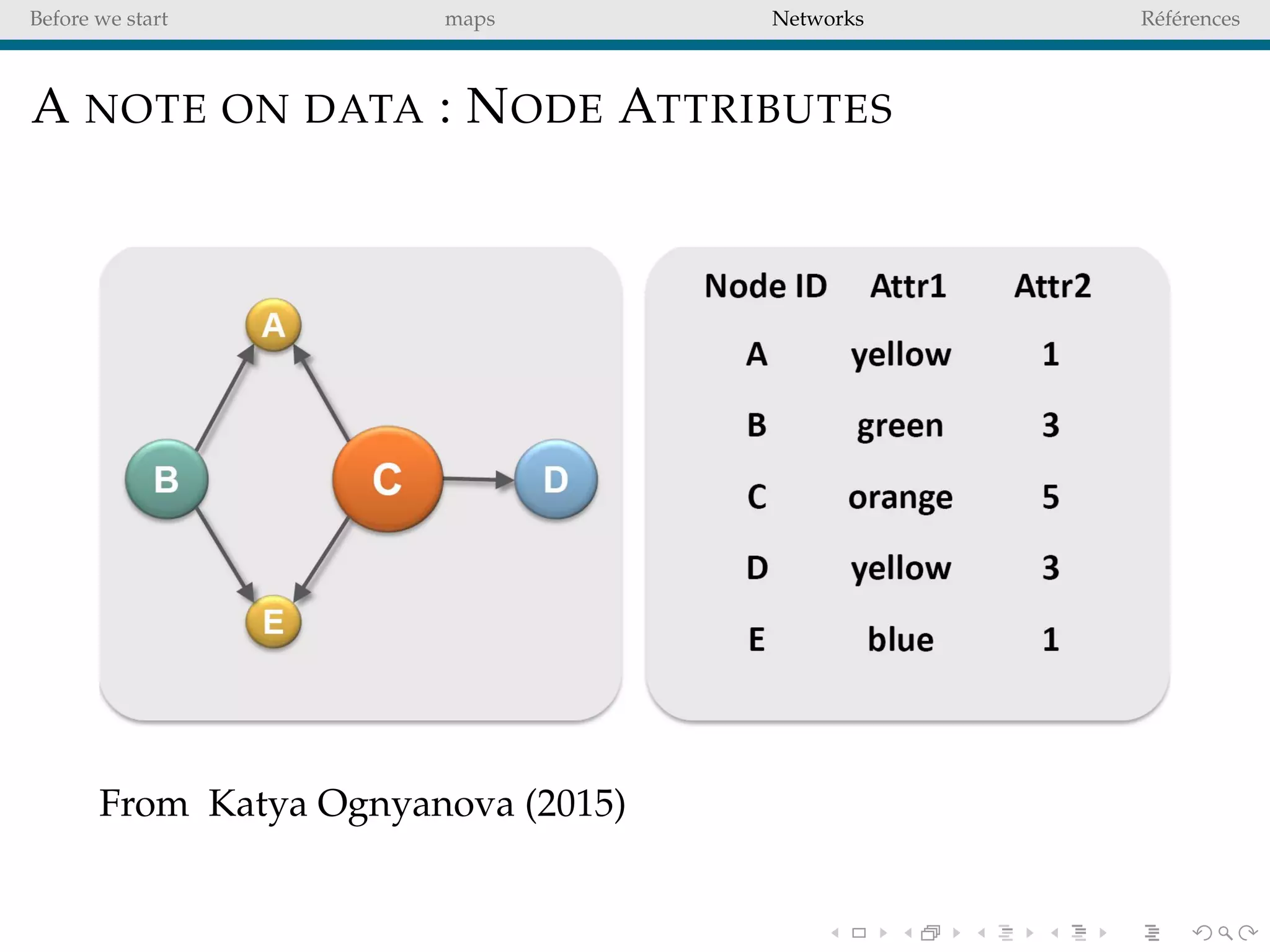
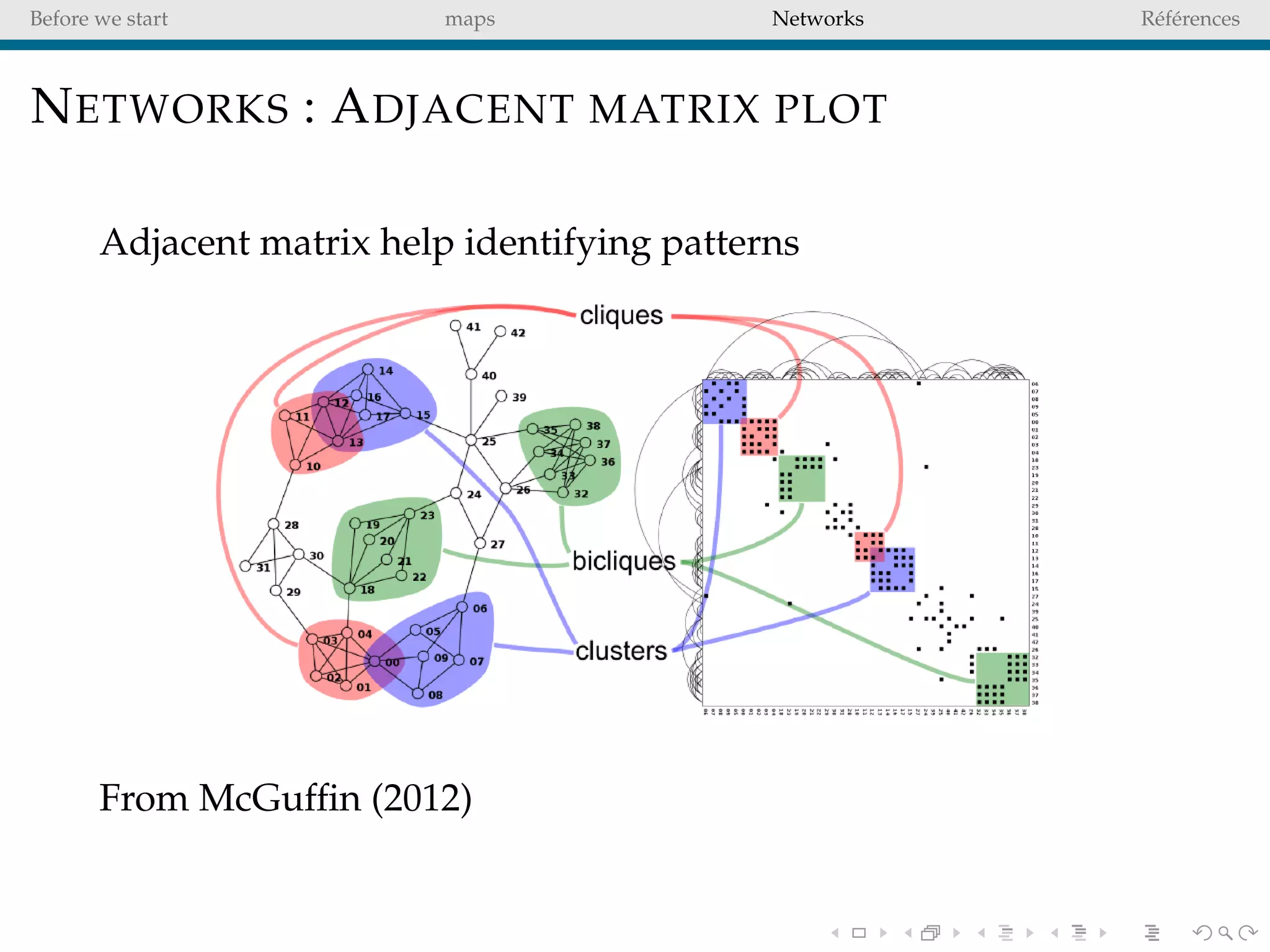
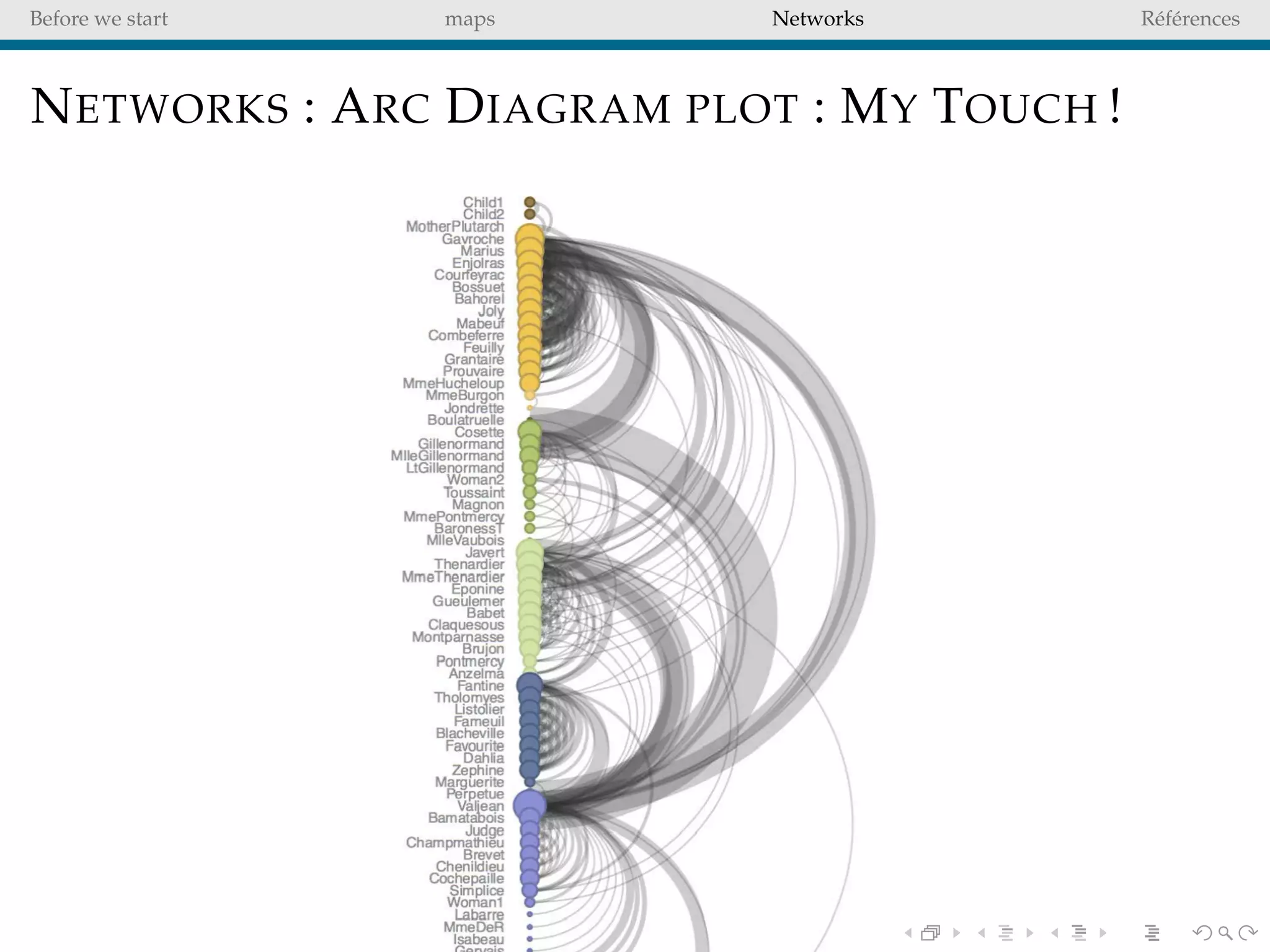
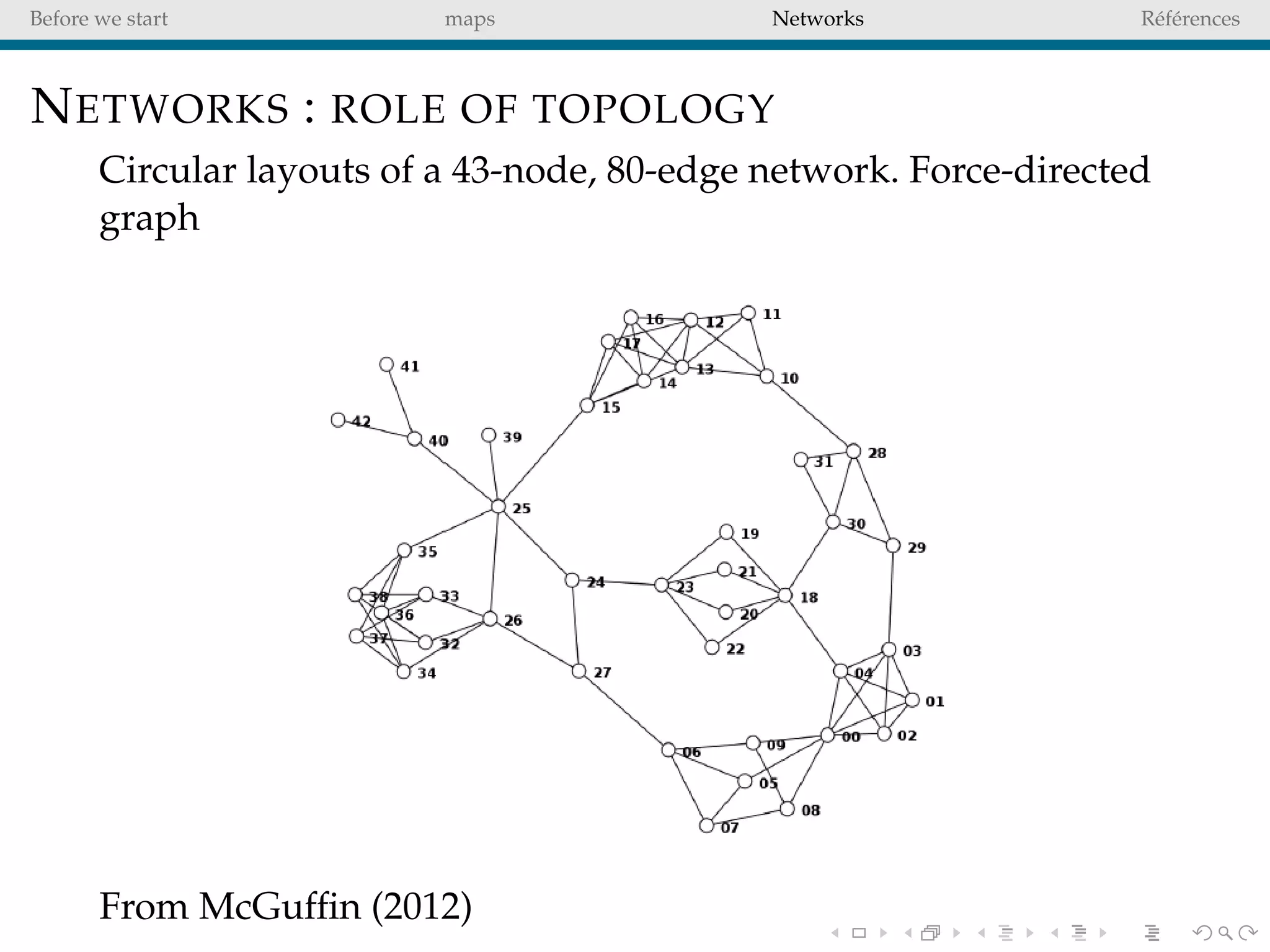
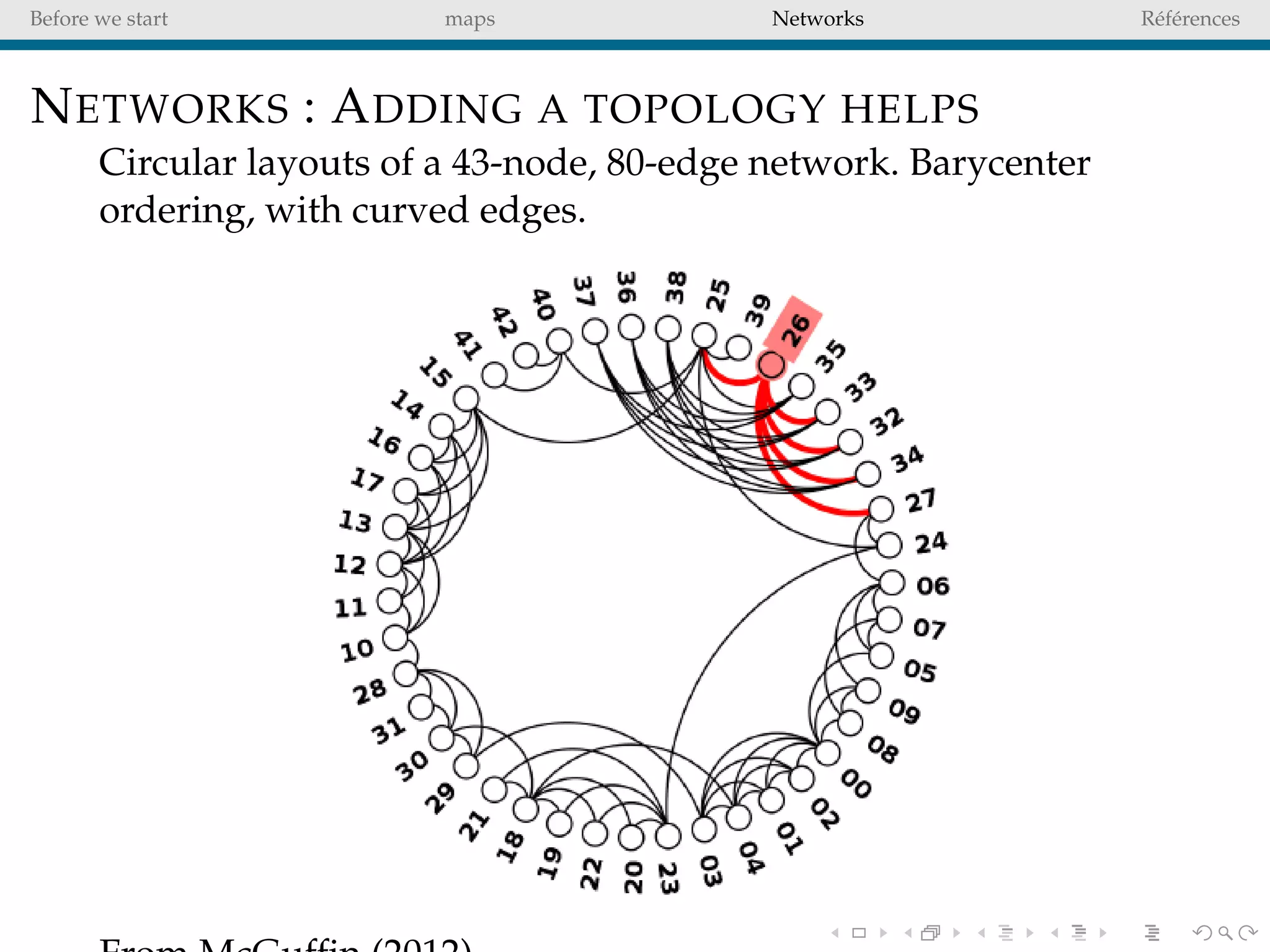
The document delves into the concepts of data visualization, focusing on its goals of data exploration and representation, and discusses how visuals can facilitate statistical comparisons and answer questions. It critiques common issues with map representations, especially in the context of election data, highlighting the potential for misrepresentation and complexity in statistical maps. Additionally, the document addresses the intricacies of network analysis, emphasizing the challenges of adequately representing relationships and the importance of clear visual rules.

Embed presentation

1 / 134
2 / 134
3 / 134
4 / 134
5 / 134
6 / 134
7 / 134
8 / 134
9 / 134
10 / 134
11 / 134
12 / 134
13 / 134
14 / 134
15 / 134
16 / 134
17 / 134
18 / 134
19 / 134
20 / 134
21 / 134
22 / 134
23 / 134
24 / 134
25 / 134
26 / 134
27 / 134
28 / 134
29 / 134
30 / 134
31 / 134
32 / 134
33 / 134
34 / 134
35 / 134
36 / 134
37 / 134
38 / 134
39 / 134
40 / 134
41 / 134
42 / 134
43 / 134
44 / 134
45 / 134
46 / 134
47 / 134
48 / 134
49 / 134
50 / 134
51 / 134
52 / 134
53 / 134
54 / 134
55 / 134
56 / 134
57 / 134
58 / 134
59 / 134
60 / 134
61 / 134
62 / 134
63 / 134
64 / 134
65 / 134
66 / 134
67 / 134
68 / 134
69 / 134
70 / 134
71 / 134
72 / 134
73 / 134
74 / 134
75 / 134
76 / 134
77 / 134
78 / 134
79 / 134
80 / 134
81 / 134
82 / 134
83 / 134
84 / 134
85 / 134
86 / 134
87 / 134
88 / 134
89 / 134
90 / 134
91 / 134
92 / 134
93 / 134
94 / 134
95 / 134
96 / 134
97 / 134
98 / 134
99 / 134
100 / 134
101 / 134
102 / 134
103 / 134
104 / 134
105 / 134
106 / 134
107 / 134
108 / 134
109 / 134
110 / 134
111 / 134
112 / 134
113 / 134
114 / 134
115 / 134
116 / 134
117 / 134
118 / 134
119 / 134
120 / 134
121 / 134
122 / 134
123 / 134
124 / 134
125 / 134
126 / 134
127 / 134
128 / 134
129 / 134
130 / 134
131 / 134
132 / 134
133 / 134
134 / 134
Before we start maps Networks Références Maps& Networks : Why and How to Visualize ? Christophe Bontemps Toulouse School of Economics, INRA @Xtophe_Bontemps
Before we start maps Networks Références MY JOB
Before we start maps Networks Références WHAT IS DATA VISUALIZATION ? Data visualisation serves at least two main purposes : Data exploration Graphs as visual tests, comparisons (short time to built and to read)
Before we start maps Networks Références WHAT IS DATA VISUALIZATION ? Data visualisation serves at least two main purposes : Data exploration Graphs as visual tests, comparisons (short time to built and to read) Data representation Summaries, storytelling (long time to build, short time to read)
Before we start maps Networks Références WHAT IS DATA VISUALIZATION ? Data visualisation serves at least two main purposes : Data exploration Graphs as visual tests, comparisons (short time to built and to read) Data representation Summaries, storytelling (long time to build, short time to read) The problem is that : “ Communicating implies simplification data exploration implies exhaustivity”
Before we start maps Networks Références SUMMARY OF PREVIOUS EPISODES From the perspective of the reader, “data visualisation” are implicitly or explicitly comparisons or even tests (in the statistical sense). Graphics should help questioning
Before we start maps Networks Références SUMMARY OF PREVIOUS EPISODES From the perspective of the reader, “data visualisation” are implicitly or explicitly comparisons or even tests (in the statistical sense). Graphics should help questioning They should provide elements, to answer legitimate questions (or, at least show the data)
Before we start maps Networks Références SUMMARY OF PREVIOUS EPISODES From the perspective of the reader, “data visualisation” are implicitly or explicitly comparisons or even tests (in the statistical sense). Graphics should help questioning They should provide elements, to answer legitimate questions (or, at least show the data) If the question implies comparison, they should truthfully show the comparison
Before we start maps Networks Références THE BIG PICTURE
Before we start maps Networks Références THE BIG PICTURE
Before we start maps Networks Références THE BIG PICTURE
Before we start maps Networks Références THE BIG PICTURE
Before we start maps Networks Références THE BIG PICTURE
Before we start maps Networks Références THE BIG PICTURE
Before we start maps Networks Références THE BIG PICTURE
Before we start maps Networks Références TO CITE A FEW “All graphs are comparisons” ...
Before we start maps Networks Références TO CITE A FEW “All graphs are comparisons” ... “All of statistics are comparisons (too).” Gelman (2004)
Before we start maps Networks Références TO CITE A FEW “All graphs are comparisons” ... “All of statistics are comparisons (too).” Gelman (2004) “ The human eye acts is a broad feature detector and general statistical test”. Buja et al. (2009)
Before we start maps Networks Références TO CITE A FEW “All graphs are comparisons” ... “All of statistics are comparisons (too).” Gelman (2004) “ The human eye acts is a broad feature detector and general statistical test”. Buja et al. (2009) “There are no “good” nor “bad” graphics (...), there are graphics answering legitimate questions and graphics that do not answer question at all ” Bertin (1981)
Before we start maps Networks Références TO CITE A FEW “All graphs are comparisons” ... “All of statistics are comparisons (too).” Gelman (2004) “ The human eye acts is a broad feature detector and general statistical test”. Buja et al. (2009) “There are no “good” nor “bad” graphics (...), there are graphics answering legitimate questions and graphics that do not answer question at all ” Bertin (1981) “Above all, show the data” Tufte (2001)
Before we start maps Networks Références WHAT’S A MAP ? Visual representation of geographical information and/or spatial data A (statistical) map is a summary of data (to be compared with pictures)
Before we start maps Networks Références WHAT’S A MAP ? Visual representation of geographical information and/or spatial data A (statistical) map is a summary of data (to be compared with pictures) Many types of maps
Before we start maps Networks Références WHAT’S A MAP ? Visual representation of geographical information and/or spatial data A (statistical) map is a summary of data (to be compared with pictures) Many types of maps What question can ask to a Map ?
Before we start maps Networks Références WHAT’S A MAP ? Visual representation of geographical information and/or spatial data A (statistical) map is a summary of data (to be compared with pictures) Many types of maps What question can ask to a Map ? Many rules for drawing a map !
Before we start maps Networks Références A CASE STUDY : ELECTIONS Most of the election’s reports are maps : legitimate questions What happened ?
Before we start maps Networks Références A CASE STUDY : ELECTIONS Most of the election’s reports are maps : legitimate questions What happened ? How can I see the most important changes ?
Before we start maps Networks Références A CASE STUDY : ELECTIONS Most of the election’s reports are maps : legitimate questions What happened ? How can I see the most important changes ? Which are the states that vote the most for Clinton ? For Trump ?
Before we start maps Networks Références A CASE STUDY : ELECTIONS Most of the election’s reports are maps : legitimate questions What happened ? How can I see the most important changes ? Which are the states that vote the most for Clinton ? For Trump ? Can I rank the importance of each state in the outcome ?
Before we start maps Networks Références A CASE STUDY : ELECTIONS 2016 results as a map : Washington Post
Before we start maps Networks Références A CASE STUDY : ELECTIONS 2012 results as a map : New York Time
Before we start maps Networks Références A CASE STUDY : ELECTIONS 2008 results as a map : New York Time
Before we start maps Networks Références A CASE STUDY : ELECTIONS What’s wrong ? I cannot see anything ! I cannot answer legitimate questions ! Quantitative information is over represented in "large" states
Before we start maps Networks Références A CASE STUDY : ELECTIONS What’s wrong ? I cannot see anything ! I cannot answer legitimate questions ! Quantitative information is over represented in "large" states Easy to see the difference between states
Before we start maps Networks Références A CASE STUDY : ELECTIONS What’s wrong ? I cannot see anything ! I cannot answer legitimate questions ! Quantitative information is over represented in "large" states Easy to see the difference between states Easy to see the results for one state
Before we start maps Networks Références A CASE STUDY : ELECTIONS What’s wrong ? I cannot see anything ! I cannot answer legitimate questions ! Quantitative information is over represented in "large" states Easy to see the difference between states Easy to see the results for one state Easy to see "regions" of the same colour
Before we start maps Networks Références A CASE STUDY : ELECTIONS What’s wrong ? I cannot see anything ! I cannot answer legitimate questions ! Quantitative information is over represented in "large" states Easy to see the difference between states Easy to see the results for one state Easy to see "regions" of the same colour Only the "raw" elements are visible, not the details (limited questions)
Before we start maps Networks Références A CASE STUDY : ELECTIONS Maybe a better map ? From Financial Times blog From Financial Times
Before we start maps Networks Références A CASE STUDY : ELECTIONS 2012 results as a map : New York Time
Before we start maps Networks Références A CASE STUDY : ELECTIONS Maybe spatial information is not the most relevant !
Before we start maps Networks Références A CASE STUDY : ELECTIONS Maybe spatial information is not the most relevant !
Before we start maps Networks Références A CASE STUDY : ELECTIONS Or if really geography matters (2004 campaign) : From Andrew Gelman’s Blog. Each pixel represents 1,000 votes.
Before we start maps Networks Références GEOGRAPHY EXISTS IN THE DATA, BUT IS NOT THE MATTER OF COMPARISON
Before we start maps Networks Références ANOTHER GOOD EXAMPLE FOR NOT USING A MAP From Our World in Data
Before we start maps Networks Références EXAMPLES OF MAPS MISSISSIPPI MEANDERS The interest here is to compare location, lines,
Before we start maps Networks Références AIR MAP OF THE WORLD (1943)
Before we start maps Networks Références THE LONDON COUNTY COUNCIL BOMB DAMAGE MAPS, 1939-1945
Before we start maps Networks Références AIR ROUTE MAPS : AARON KOBLIN
Before we start maps Networks Références PARTIAL CONCLUSION Maps are useful
Before we start maps Networks Références PARTIAL CONCLUSION Maps are useful There are rules (over representation of large area, colorpleth,etc..)
Before we start maps Networks Références PARTIAL CONCLUSION Maps are useful There are rules (over representation of large area, colorpleth,etc..) Statistical maps are difficult to built :
Before we start maps Networks Références PARTIAL CONCLUSION Maps are useful There are rules (over representation of large area, colorpleth,etc..) Statistical maps are difficult to built : How to show uncertainty on a map ?
Before we start maps Networks Références PARTIAL CONCLUSION Maps are useful There are rules (over representation of large area, colorpleth,etc..) Statistical maps are difficult to built : How to show uncertainty on a map ? How to show correlations on a map ?
Before we start maps Networks Références PARTIAL CONCLUSION Maps are useful There are rules (over representation of large area, colorpleth,etc..) Statistical maps are difficult to built : How to show uncertainty on a map ? How to show correlations on a map ? Comparisons are limited (only geographical)
Before we start maps Networks Références PARTIAL CONCLUSION Maps are useful There are rules (over representation of large area, colorpleth,etc..) Statistical maps are difficult to built : How to show uncertainty on a map ? How to show correlations on a map ? Comparisons are limited (only geographical) Maps can help select, or highlight other elements (see D3.js, dashboards, or GeoXP package)
Before we start maps Networks Références QUESTIONS ON NETWORKS : There are many challenges in statistical networks analysis : Statistics on networks are quite difficult to handle
Before we start maps Networks Références QUESTIONS ON NETWORKS : There are many challenges in statistical networks analysis : Statistics on networks are quite difficult to handle Many types of networks
Before we start maps Networks Références QUESTIONS ON NETWORKS : There are many challenges in statistical networks analysis : Statistics on networks are quite difficult to handle Many types of networks Questions related to networks are hard to state (fuzzy or unarticulated)
Before we start maps Networks Références QUESTIONS ON NETWORKS : There are many challenges in statistical networks analysis : Statistics on networks are quite difficult to handle Many types of networks Questions related to networks are hard to state (fuzzy or unarticulated) Visualizations are barely readable (decoding is hard !)
Before we start maps Networks Références IS THIS A NETWORK OR A MAP ?
Before we start maps Networks Références IS THIS A NETWORK OR A MAP ? This is a Map showing links (air connections) between geographical entities.
Before we start maps Networks Références IS THIS A NETWORK OR A MAP ? This is a Map showing links (air connections) between geographical entities. This is “a collection of interconnected things”, (Oxford Englis Dictionary)
Before we start maps Networks Références TYPES OF NETWORKS Adjacency Networks
Before we start maps Networks Références TYPES OF NETWORKS Adjacency Networks
Before we start maps Networks Références TYPES OF NETWORKS Adjacency Networks Bipartite Networks
Before we start maps Networks Références TYPES OF NETWORKS Adjacency Networks Bipartite Networks
Before we start maps Networks Références TYPES OF NETWORKS Adjacency Networks Bipartite Networks From bipartite, one can create adjacency
Before we start maps Networks Références TYPES OF NETWORKS Adjacency Networks Bipartite Networks From bipartite, one can create adjacency
Before we start maps Networks Références TYPES OF NETWORKS Adjacency Networks Bipartite Networks From bipartite, one can create adjacency From Heijmans et al. (2014), and Kolaczyk (2009)
Before we start maps Networks Références TYPES OF NETWORKS Undirected (A& B ’know each other’) and directed (A ’owe money to’ B)
Before we start maps Networks Références TYPES OF NETWORKS Undirected (A& B ’know each other’) and directed (A ’owe money to’ B)
Before we start maps Networks Références TYPES OF NETWORKS Undirected (A& B ’know each other’) and directed (A ’owe money to’ B) From Kolaczyk and Csárdi (2014)
Before we start maps Networks Références FAMILIES OF GRAPHS
Before we start maps Networks Références FAMILIES OF GRAPHS Complete (top left) ; ring (top right) ; tree (bottom left) ; and star (bottom right)
Before we start maps Networks Références FAMILIES OF GRAPHS Complete (top left) ; ring (top right) ; tree (bottom left) ; and star (bottom right) From Kolaczyk and Csárdi (2014)
Before we start maps Networks Références A CLASSICAL NETWORK EXAMPLE Relationships of all of Victor Hugo’s characters of "Les Miserables". Data composed of nodes (characters) + Links (strength of links) http://bl.ocks.org/mbostock/4062045
Before we start maps Networks Références A CLASSICAL NETWORK EXAMPLE Relationships of all of Victor Hugo’s characters of "Les Miserables". Data composed of nodes (characters) + Links (strength of links) Nodes can be coloured (information on characters) http://bl.ocks.org/mbostock/4062045
Before we start maps Networks Références A CLASSICAL NETWORK EXAMPLE Relationships of all of Victor Hugo’s characters of "Les Miserables". Data composed of nodes (characters) + Links (strength of links) Nodes can be coloured (information on characters) Force-directed graph http://bl.ocks.org/mbostock/4062045
Before we start maps Networks Références A CLASSICAL NETWORK EXAMPLE Relationships of all of Victor Hugo’s characters of "Les Miserables". Data composed of nodes (characters) + Links (strength of links) Nodes can be coloured (information on characters) Force-directed graph Here, done with d3.js http://bl.ocks.org/mbostock/4062045
Before we start maps Networks Références A CLASSICAL NETWORK EXAMPLE Relationships of all of Victor Hugo’s characters of "Les Miserables".
Before we start maps Networks Références A CLASSICAL NETWORK EXAMPLE What do we see ? An overview of problems : Not the same graph each time (nondeterminstic algorithm)
Before we start maps Networks Références A CLASSICAL NETWORK EXAMPLE What do we see ? An overview of problems : Not the same graph each time (nondeterminstic algorithm) Spacial position does not encode attributes (algorithm-driven)
Before we start maps Networks Références A CLASSICAL NETWORK EXAMPLE What do we see ? An overview of problems : Not the same graph each time (nondeterminstic algorithm) Spacial position does not encode attributes (algorithm-driven) Proximity (of nodes) sometimes meaningful sometimes arbitrary. Artefacts created (some nodes “pushed back”.)
Before we start maps Networks Références A CLASSICAL NETWORK EXAMPLE What do we see ? An overview of problems : Not the same graph each time (nondeterminstic algorithm) Spacial position does not encode attributes (algorithm-driven) Proximity (of nodes) sometimes meaningful sometimes arbitrary. Artefacts created (some nodes “pushed back”.) What can we learn ? What can we compare ?
Before we start maps Networks Références A CLASSICAL NETWORK EXAMPLE What do we see ? An overview of problems : Not the same graph each time (nondeterminstic algorithm) Spacial position does not encode attributes (algorithm-driven) Proximity (of nodes) sometimes meaningful sometimes arbitrary. Artefacts created (some nodes “pushed back”.) What can we learn ? What can we compare ? Alternative view with bezier http://bl.ocks.org/mbostock/4600693
Before we start maps Networks Références HOW DOES IT WORK ? A vast family of Force-directed placement network representation Placing nodes randomly (put colour on groups)
Before we start maps Networks Références HOW DOES IT WORK ? A vast family of Force-directed placement network representation Placing nodes randomly (put colour on groups) Iteratively refine location following “forces”
Before we start maps Networks Références HOW DOES IT WORK ? A vast family of Force-directed placement network representation Placing nodes randomly (put colour on groups) Iteratively refine location following “forces” Nodes have “repulsive forces” (like electrons)
Before we start maps Networks Références HOW DOES IT WORK ? A vast family of Force-directed placement network representation Placing nodes randomly (put colour on groups) Iteratively refine location following “forces” Nodes have “repulsive forces” (like electrons) Links are “springs” (strength proportional to nb of connections)
Before we start maps Networks Références HOW DOES IT WORK ? A vast family of Force-directed placement network representation Placing nodes randomly (put colour on groups) Iteratively refine location following “forces” Nodes have “repulsive forces” (like electrons) Links are “springs” (strength proportional to nb of connections) Apply “some other rules‘” (see next slides)
Before we start maps Networks Références HOW DOES IT WORK ? A vast family of Force-directed placement network representation Placing nodes randomly (put colour on groups) Iteratively refine location following “forces” Nodes have “repulsive forces” (like electrons) Links are “springs” (strength proportional to nb of connections) Apply “some other rules‘” (see next slides) Iterate (computationally demanding)
Before we start maps Networks Références HOW DOES IT WORK ? A vast family of Force-directed placement network representation Placing nodes randomly (put colour on groups) Iteratively refine location following “forces” Nodes have “repulsive forces” (like electrons) Links are “springs” (strength proportional to nb of connections) Apply “some other rules‘” (see next slides) Iterate (computationally demanding) Wait until it stabilizes (even on a local equilibrium)
Before we start maps Networks Références FORCE-DIRECTED GRAPHS : Physically-based model + aesthetic touch + fuzzy stuff... From Tunkelang (1998)
Before we start maps Networks Références RULES FOR “NODE-LINK” REPRESENTATIONS Node-links representation follow rules : General rules : From Katya Ognyanova (2015) and Bahoken et al. (2013)
Before we start maps Networks Références RULES FOR “NODE-LINK” REPRESENTATIONS Node-links representation follow rules : General rules : Most connected nodes in the center From Katya Ognyanova (2015) and Bahoken et al. (2013)
Before we start maps Networks Références RULES FOR “NODE-LINK” REPRESENTATIONS Node-links representation follow rules : General rules : Most connected nodes in the center Less connected nodes at the periphery From Katya Ognyanova (2015) and Bahoken et al. (2013)
Before we start maps Networks Références RULES FOR “NODE-LINK” REPRESENTATIONS Node-links representation follow rules : General rules : Most connected nodes in the center Less connected nodes at the periphery Layout aesthetics rules : From Katya Ognyanova (2015) and Bahoken et al. (2013)
Before we start maps Networks Références RULES FOR “NODE-LINK” REPRESENTATIONS Node-links representation follow rules : General rules : Most connected nodes in the center Less connected nodes at the periphery Layout aesthetics rules : Minimize edge crossing From Katya Ognyanova (2015) and Bahoken et al. (2013)
Before we start maps Networks Références RULES FOR “NODE-LINK” REPRESENTATIONS Node-links representation follow rules : General rules : Most connected nodes in the center Less connected nodes at the periphery Layout aesthetics rules : Minimize edge crossing Prevent overlap From Katya Ognyanova (2015) and Bahoken et al. (2013)
Before we start maps Networks Références RULES FOR “NODE-LINK” REPRESENTATIONS Node-links representation follow rules : General rules : Most connected nodes in the center Less connected nodes at the periphery Layout aesthetics rules : Minimize edge crossing Prevent overlap Symmetry From Katya Ognyanova (2015) and Bahoken et al. (2013)
Before we start maps Networks Références RULES FOR “NODE-LINK” REPRESENTATIONS Node-links representation follow rules : General rules : Most connected nodes in the center Less connected nodes at the periphery Layout aesthetics rules : Minimize edge crossing Prevent overlap Symmetry Uniform edge length From Katya Ognyanova (2015) and Bahoken et al. (2013)
Before we start maps Networks Références LAYOUT AESTHETICS From Katya Ognyanova (2015)
Before we start maps Networks Références A NOTE ON DATA : MATRIX From Katya Ognyanova (2015)
Before we start maps Networks Références A NOTE ON DATA : EDGE LIST From Katya Ognyanova (2015)
Before we start maps Networks Références A NOTE ON DATA : NODE LIST From Katya Ognyanova (2015)
Before we start maps Networks Références A NOTE ON DATA : NODE ATTRIBUTES From Katya Ognyanova (2015)
Before we start maps Networks Références ALTERNATIVE VIEW : ADJACENT MATRIX PLOT An adjacency matrix, where each cell ij represents an edge from vertex i to vertex j. Here, vertices represent characters in a book, while edges represent co-occurrence in a chapter. http://bost.ocks.org/mike/miserables/
Before we start maps Networks Références NETWORKS : ADJACENT MATRIX PLOT As in many example, sorting is very useful !
Before we start maps Networks Références NETWORKS : ADJACENT MATRIX PLOT Adjacent matrix help identifying patterns From McGuffin (2012)
Before we start maps Networks Références NETWORKS : ARC DIAGRAM PLOT To put some structure in the graph : Horizontal alignment From Gaston Sanchez see also McGuffin (2012)
Before we start maps Networks Références NETWORKS : ARC DIAGRAM PLOT Now we can sort ! (according to groups, and then degrees) FromGaston Sanchez
Before we start maps Networks Références NETWORKS : ARC DIAGRAM PLOT : MY TOUCH !
Before we start maps Networks Références NETWORKS : ROLE OF TOPOLOGY Circular layouts of a 43-node, 80-edge network. Force-directed graph From McGuffin (2012)
Before we start maps Networks Références NETWORKS : ADDING A TOPOLOGY HELPS Circular layouts of a 43-node, 80-edge network. No ordering, with curved edges. From McGuffin (2012)
Before we start maps Networks Références NETWORKS : ADDING A TOPOLOGY HELPS Circular layouts of a 43-node, 80-edge network. Barycenter ordering, with curved edges.
Before we start maps Networks Références PROBLEM 1 : IDENTIFY REFERENCE GRAPHS Random Graphs difficult to identify
Before we start maps Networks Références PROBLEM 1 : IDENTIFY REFERENCE GRAPHS Random Graphs difficult to identify
Before we start maps Networks Références PROBLEM 1 : IDENTIFY REFERENCE GRAPHS Random Graphs difficult to identify Or
Before we start maps Networks Références PROBLEM 1 : IDENTIFY REFERENCE GRAPHS Random Graphs difficult to identify Or
Before we start maps Networks Références PROBLEM 1 : IDENTIFY REFERENCE GRAPHS Random Graphs difficult to identify Or → How to do any visual test ?
Before we start maps Networks Références PROBLEM 2 : LAYOUT CHANGE PERCEPTION Three layouts of the same graph From Kolaczyk and Csárdi (2014)
Before we start maps Networks Références PROBLEM 2 : LAYOUT CHANGE PERCEPTION Three layouts of the same graph From Kolaczyk and Csárdi (2014)
Before we start maps Networks Références PROBLEM 2 : LAYOUT CHANGE PERCEPTION Three layouts of the same graph From Kolaczyk and Csárdi (2014)
Before we start maps Networks Références PROBLEM 2 : LAYOUT CHANGE PERCEPTION Three layouts of the same graph → Circular, radial, layered. From Kolaczyk and Csárdi (2014)
Before we start maps Networks Références PROBLEM 3 : DECORATION HELPS ? From Kolaczyk and Csárdi (2014)
Before we start maps Networks Références PROBLEM 3 : DECORATION HELPS ? Plain and decorated visualizations of a karate club network From Kolaczyk and Csárdi (2014)
Before we start maps Networks Références PROBLEM 4 : SCALABILITY ? (192 blogs linked by 1,431 edges indicating at least one of the two blogs referenced the other). From Kolaczyk and Csárdi (2014)
Before we start maps Networks Références PROBLEM 4 : SCALABILITY ? French political blog network (192 blogs linked by 1,431 edges indicating at least one of the two blogs referenced the other). From Kolaczyk and Csárdi (2014)
Before we start maps Networks Références PROBLEM 4 : SCALABILITY ? French political blog network Towards an "hairball" + complexity is O(N2 v) (192 blogs linked by 1,431 edges indicating at least one of the two blogs referenced the other). From Kolaczyk and Csárdi (2014)
Before we start maps Networks Références SOLUTIONS : SPLIT ? From Kolaczyk and Csárdi (2014)
Before we start maps Networks Références SOLUTIONS : SPLIT ? Two ego-centric views of the karate club network From Kolaczyk and Csárdi (2014)
Before we start maps Networks Références SOLUTIONS : AGGREGATE ? From Kolaczyk and Csárdi (2014)
Before we start maps Networks Références SOLUTIONS : AGGREGATE ? French political blog network at the level of political parties From Kolaczyk and Csárdi (2014)
Before we start maps Networks Références REFERENCES I Bahoken, F., Beauguitte, L., and Lhomme, S. (2013). La visualisation des réseaux. principes, enjeux et perspectives. Bertin, J. (1981). Théorie matricielle de la graphique. Communication et langages, 48(1) :62–74. Buja, A., Cook, D., Hofmann, H., Lawrence, M., Lee, E.-K., Swayne, D. F., and Wickham, H. (2009). Statistical inference for exploratory data analysis and model diagnostics. Philosophical Transactions of the Royal Society of London A : Mathematical, Physical and Engineering Sciences, 367(1906) :4361–4383. Gelman, A. (2004). Exploratory data analysis for complex models. Journal of Computational and Graphical Statistics, 13(4). Heijmans, R., Heuver, R., Levallois, C., and Lelyveld, I. V. (2014). Dynamic visualization of large transaction networks : the daily dutch overnight money market. Kolaczyk, E. D. (2009). Statistical Analysis of Network Data : Methods and Models. Springer Series in Statistics. Springer-Verlag New York, 1 edition. Kolaczyk, E. D. and Csárdi, G. (2014). Statistical Analysis of Network Data with R. Use R ! 65. Springer-Verlag New York, 1 edition.
Before we start maps Networks Références REFERENCES II McGuffin, M. J. (2012). Simple algorithms for network visualization : A tutorial. Tsinghua Science and Technology, 17(4) :383–398. Ognyanova, K. (2015). R network visualization workshop. In POLNET 2015, Portland OR. Tufte, E. R. (2001). The Visual Display of Quantitative Information. Graphics Press, 2 edition. Tunkelang, D. (1998). A Numerical Optimization Approach to Graph Drawing. PhD thesis, Dissertation, Carnegie Mellon University, School of Computer Science.

More Related Content

PDF
Meetup D3.js Paris - Christophe Blefari - Equancy
byChristophe Blefari
 
PDF
Information Visualization Workshop, ASIS&T 2015
byJoseph Ryan
 
PPTX
Data visualisation as a campaign tool for change
byLittle Web Giants
 
PDF
Network Mapping & Data Storytelling for Beginners
byRenaud Clément
 
PPTX
Unit III.pptx
byKennyPratheepKumar
 
PPTX
TYBSC IT PGIS Unit V Data Visualization
byArti Parab Academics
 
PDF
Painting a clearer picture
byAna Figueiras
 
PDF
12. Map Visualization .pdf
byssusercc3ff71
 
Meetup D3.js Paris - Christophe Blefari - Equancy
byChristophe Blefari
 
Information Visualization Workshop, ASIS&T 2015
byJoseph Ryan
 
Data visualisation as a campaign tool for change
byLittle Web Giants
 
Network Mapping & Data Storytelling for Beginners
byRenaud Clément
 
Unit III.pptx
byKennyPratheepKumar
 
TYBSC IT PGIS Unit V Data Visualization
byArti Parab Academics
 
Painting a clearer picture
byAna Figueiras
 
12. Map Visualization .pdf
byssusercc3ff71
 

Similar to Meetup Maps & Networks: Why and How to visualize

PPTX
Data Visulalization
byGirish Khanzode
 
PDF
Introduction to Information Visualization (Part 2)
byAndrew Vande Moere
 
PPTX
Data Visualization1.pptx
byqwtadhsaber
 
PDF
Data Journalism - Storytelling with Data
byBahareh Heravi
 
PPTX
SEMINAR Presentation ppt.pptx
byWageYado
 
PPTX
SEMINAR Presentation ppt.pptx
byWageYado
 
PDF
Data Visualization in the Newsroom
byCarl V. Lewis
 
PPT
Information visualisation
byhcicourse
 
PDF
Transcript - Data Visualisation - Design and Principals
byARDC
 
PPTX
Making abstract data visible
byPriyanshi Jain
 
PPTX
Making sense of data visually: A modern look at datavisualization
byVladimir Milev
 
PPT
Manila Workshop Infographics
byZoltan Nagy
 
PDF
Pratiques historiques et actuelles
bymarionboucharlat
 
PDF
Making an Impact With Data Visualization
byUNCResearchHub
 
PDF
Dublinked Data Visualisation Competition Launch Event - Andy Kirk Presentation
byDublinked .
 
PDF
Data visualization tools & techniques - 1
byKorivi Sravan Kumar
 
PDF
European creativity festival 2014: DataViz workshop
byOutliers Collective
 
PPTX
Data Visualization
byMarco Torchiano
 
PDF
Lies, damned lies & dataviz
byAndrew Clegg
 
PPTX
Introduction to Data Visualisation - Andrew Errity
byaerrity
 
Data Visulalization
byGirish Khanzode
 
Introduction to Information Visualization (Part 2)
byAndrew Vande Moere
 
Data Visualization1.pptx
byqwtadhsaber
 
Data Journalism - Storytelling with Data
byBahareh Heravi
 
SEMINAR Presentation ppt.pptx
byWageYado
 
SEMINAR Presentation ppt.pptx
byWageYado
 
Data Visualization in the Newsroom
byCarl V. Lewis
 
Information visualisation
byhcicourse
 
Transcript - Data Visualisation - Design and Principals
byARDC
 
Making abstract data visible
byPriyanshi Jain
 
Making sense of data visually: A modern look at datavisualization
byVladimir Milev
 
Manila Workshop Infographics
byZoltan Nagy
 
Pratiques historiques et actuelles
bymarionboucharlat
 
Making an Impact With Data Visualization
byUNCResearchHub
 
Dublinked Data Visualisation Competition Launch Event - Andy Kirk Presentation
byDublinked .
 
Data visualization tools & techniques - 1
byKorivi Sravan Kumar
 
European creativity festival 2014: DataViz workshop
byOutliers Collective
 
Data Visualization
byMarco Torchiano
 
Lies, damned lies & dataviz
byAndrew Clegg
 
Introduction to Data Visualisation - Andrew Errity
byaerrity
 

Recently uploaded

PPTX
AI in Business course, Power BI BNU LHE.
bymuhammadasad96468
 
PDF
AI 1.pdf AI in Business Training - Revolutionizing Business Operations
byCA Suvidha Chaplot
 
PPTX
25CSM2R26_AditiMIshra_WDSAttackcybe.pptx
bydrfareesafirdouse
 
PPTX
2ai_mockinterview.pptx hjijjjjjjjjjnhhbh
bypankajponia112
 
PPTX
project physics.pptx for class 12th students for therir schhol and enough
bykhantdevanshi12
 
PPTX
Sales_Analysis_Presentation.pptx dashboard
bydheerendras984
 
PPT
unit-3 Introduction to drawing and instruments part-2.ppt
byalemayehuc1
 
PDF
CSE550_ Lecture 02robosssssssssssstik.pdf
byfarfauziar
 
PPTX
Statistical Analysis for Researchers - Presentation - Lecture Two.pptx
byAmgad Fahmy
 
PDF
Azure Data Factory Overview for SSIS Developers.pdf
bySrinivas V
 
PPTX
ict_presentation_final_final_final[1].pptx
bysaadabdulghafoor24
 
PPTX
Ch6 Automata & Complexity Theory 2016.pptx
bytechnologyn387
 
PPTX
Vector Space Modelin Information Storage and Retrieval .pptx
byhermelamisganew
 
PPTX
LinkedIn Lead Generation expert for B2B Lead Generation
byMdBelalSharif1
 
PDF
CLINICO-SOCIAL CASE DISCUSSION-antenatal
bymlaksh790
 
PPTX
Pakistan Tableau User Group Event: A guide to Salesforce Certified Data Analyst
byWaqarAhmedShaikh8
 
PPTX
Testing-Results-and-Outcomes (1).pptx dfw
bySrini Vasan
 
PDF
AI 30.pdf Practical Insights from CA Suvidha Chaplot for AI Implementation in...
byCA Suvidha Chaplot
 
PPTX
1-FUEL IN A DIESEL ENGINE UNDERSTANDING AND KNOWLEDGE CONCEPTS
byMarkFenwick10
 
PDF
apidays Paris 2025 | Optimize your architecture for the next wave of AI-infus...
byapidays
 
AI in Business course, Power BI BNU LHE.
bymuhammadasad96468
 
AI 1.pdf AI in Business Training - Revolutionizing Business Operations
byCA Suvidha Chaplot
 
25CSM2R26_AditiMIshra_WDSAttackcybe.pptx
bydrfareesafirdouse
 
2ai_mockinterview.pptx hjijjjjjjjjjnhhbh
bypankajponia112
 
project physics.pptx for class 12th students for therir schhol and enough
bykhantdevanshi12
 
Sales_Analysis_Presentation.pptx dashboard
bydheerendras984
 
unit-3 Introduction to drawing and instruments part-2.ppt
byalemayehuc1
 
CSE550_ Lecture 02robosssssssssssstik.pdf
byfarfauziar
 
Statistical Analysis for Researchers - Presentation - Lecture Two.pptx
byAmgad Fahmy
 
Azure Data Factory Overview for SSIS Developers.pdf
bySrinivas V
 
ict_presentation_final_final_final[1].pptx
bysaadabdulghafoor24
 
Ch6 Automata & Complexity Theory 2016.pptx
bytechnologyn387
 
Vector Space Modelin Information Storage and Retrieval .pptx
byhermelamisganew
 
LinkedIn Lead Generation expert for B2B Lead Generation
byMdBelalSharif1
 
CLINICO-SOCIAL CASE DISCUSSION-antenatal
bymlaksh790
 
Pakistan Tableau User Group Event: A guide to Salesforce Certified Data Analyst
byWaqarAhmedShaikh8
 
Testing-Results-and-Outcomes (1).pptx dfw
bySrini Vasan
 
AI 30.pdf Practical Insights from CA Suvidha Chaplot for AI Implementation in...
byCA Suvidha Chaplot
 
1-FUEL IN A DIESEL ENGINE UNDERSTANDING AND KNOWLEDGE CONCEPTS
byMarkFenwick10
 
apidays Paris 2025 | Optimize your architecture for the next wave of AI-infus...
byapidays
 

Meetup Maps & Networks: Why and How to visualize

  • 1.
    Before we startmaps Networks Références Maps& Networks : Why and How to Visualize ? Christophe Bontemps Toulouse School of Economics, INRA @Xtophe_Bontemps
  • 2.
    Before we startmaps Networks Références MY JOB
  • 3.
    Before we startmaps Networks Références WHAT IS DATA VISUALIZATION ? Data visualisation serves at least two main purposes : Data exploration Graphs as visual tests, comparisons (short time to built and to read)
  • 4.
    Before we startmaps Networks Références WHAT IS DATA VISUALIZATION ? Data visualisation serves at least two main purposes : Data exploration Graphs as visual tests, comparisons (short time to built and to read) Data representation Summaries, storytelling (long time to build, short time to read)
  • 5.
    Before we startmaps Networks Références WHAT IS DATA VISUALIZATION ? Data visualisation serves at least two main purposes : Data exploration Graphs as visual tests, comparisons (short time to built and to read) Data representation Summaries, storytelling (long time to build, short time to read) The problem is that : “ Communicating implies simplification data exploration implies exhaustivity”
  • 6.
    Before we startmaps Networks Références SUMMARY OF PREVIOUS EPISODES From the perspective of the reader, “data visualisation” are implicitly or explicitly comparisons or even tests (in the statistical sense). Graphics should help questioning
  • 7.
    Before we startmaps Networks Références SUMMARY OF PREVIOUS EPISODES From the perspective of the reader, “data visualisation” are implicitly or explicitly comparisons or even tests (in the statistical sense). Graphics should help questioning They should provide elements, to answer legitimate questions (or, at least show the data)
  • 8.
    Before we startmaps Networks Références SUMMARY OF PREVIOUS EPISODES From the perspective of the reader, “data visualisation” are implicitly or explicitly comparisons or even tests (in the statistical sense). Graphics should help questioning They should provide elements, to answer legitimate questions (or, at least show the data) If the question implies comparison, they should truthfully show the comparison
  • 9.
    Before we startmaps Networks Références THE BIG PICTURE
  • 10.
    Before we startmaps Networks Références THE BIG PICTURE
  • 11.
    Before we startmaps Networks Références THE BIG PICTURE
  • 12.
    Before we startmaps Networks Références THE BIG PICTURE
  • 13.
    Before we startmaps Networks Références THE BIG PICTURE
  • 14.
    Before we startmaps Networks Références THE BIG PICTURE
  • 15.
    Before we startmaps Networks Références THE BIG PICTURE
  • 16.
    Before we startmaps Networks Références TO CITE A FEW “All graphs are comparisons” ...
  • 17.
    Before we startmaps Networks Références TO CITE A FEW “All graphs are comparisons” ... “All of statistics are comparisons (too).” Gelman (2004)
  • 18.
    Before we startmaps Networks Références TO CITE A FEW “All graphs are comparisons” ... “All of statistics are comparisons (too).” Gelman (2004) “ The human eye acts is a broad feature detector and general statistical test”. Buja et al. (2009)
  • 19.
    Before we startmaps Networks Références TO CITE A FEW “All graphs are comparisons” ... “All of statistics are comparisons (too).” Gelman (2004) “ The human eye acts is a broad feature detector and general statistical test”. Buja et al. (2009) “There are no “good” nor “bad” graphics (...), there are graphics answering legitimate questions and graphics that do not answer question at all ” Bertin (1981)
  • 20.
    Before we startmaps Networks Références TO CITE A FEW “All graphs are comparisons” ... “All of statistics are comparisons (too).” Gelman (2004) “ The human eye acts is a broad feature detector and general statistical test”. Buja et al. (2009) “There are no “good” nor “bad” graphics (...), there are graphics answering legitimate questions and graphics that do not answer question at all ” Bertin (1981) “Above all, show the data” Tufte (2001)
  • 21.
    Before we startmaps Networks Références WHAT’S A MAP ? Visual representation of geographical information and/or spatial data A (statistical) map is a summary of data (to be compared with pictures)
  • 22.
    Before we startmaps Networks Références WHAT’S A MAP ? Visual representation of geographical information and/or spatial data A (statistical) map is a summary of data (to be compared with pictures) Many types of maps
  • 23.
    Before we startmaps Networks Références WHAT’S A MAP ? Visual representation of geographical information and/or spatial data A (statistical) map is a summary of data (to be compared with pictures) Many types of maps What question can ask to a Map ?
  • 24.
    Before we startmaps Networks Références WHAT’S A MAP ? Visual representation of geographical information and/or spatial data A (statistical) map is a summary of data (to be compared with pictures) Many types of maps What question can ask to a Map ? Many rules for drawing a map !
  • 25.
    Before we startmaps Networks Références A CASE STUDY : ELECTIONS Most of the election’s reports are maps : legitimate questions What happened ?
  • 26.
    Before we startmaps Networks Références A CASE STUDY : ELECTIONS Most of the election’s reports are maps : legitimate questions What happened ? How can I see the most important changes ?
  • 27.
    Before we startmaps Networks Références A CASE STUDY : ELECTIONS Most of the election’s reports are maps : legitimate questions What happened ? How can I see the most important changes ? Which are the states that vote the most for Clinton ? For Trump ?
  • 28.
    Before we startmaps Networks Références A CASE STUDY : ELECTIONS Most of the election’s reports are maps : legitimate questions What happened ? How can I see the most important changes ? Which are the states that vote the most for Clinton ? For Trump ? Can I rank the importance of each state in the outcome ?
  • 29.
    Before we startmaps Networks Références A CASE STUDY : ELECTIONS 2016 results as a map : Washington Post
  • 30.
    Before we startmaps Networks Références A CASE STUDY : ELECTIONS 2012 results as a map : New York Time
  • 31.
    Before we startmaps Networks Références A CASE STUDY : ELECTIONS 2008 results as a map : New York Time
  • 32.
    Before we startmaps Networks Références A CASE STUDY : ELECTIONS What’s wrong ? I cannot see anything ! I cannot answer legitimate questions ! Quantitative information is over represented in "large" states
  • 33.
    Before we startmaps Networks Références A CASE STUDY : ELECTIONS What’s wrong ? I cannot see anything ! I cannot answer legitimate questions ! Quantitative information is over represented in "large" states Easy to see the difference between states
  • 34.
    Before we startmaps Networks Références A CASE STUDY : ELECTIONS What’s wrong ? I cannot see anything ! I cannot answer legitimate questions ! Quantitative information is over represented in "large" states Easy to see the difference between states Easy to see the results for one state
  • 35.
    Before we startmaps Networks Références A CASE STUDY : ELECTIONS What’s wrong ? I cannot see anything ! I cannot answer legitimate questions ! Quantitative information is over represented in "large" states Easy to see the difference between states Easy to see the results for one state Easy to see "regions" of the same colour
  • 36.
    Before we startmaps Networks Références A CASE STUDY : ELECTIONS What’s wrong ? I cannot see anything ! I cannot answer legitimate questions ! Quantitative information is over represented in "large" states Easy to see the difference between states Easy to see the results for one state Easy to see "regions" of the same colour Only the "raw" elements are visible, not the details (limited questions)
  • 37.
    Before we startmaps Networks Références A CASE STUDY : ELECTIONS Maybe a better map ? From Financial Times blog From Financial Times
  • 38.
    Before we startmaps Networks Références A CASE STUDY : ELECTIONS 2012 results as a map : New York Time
  • 39.
    Before we startmaps Networks Références A CASE STUDY : ELECTIONS Maybe spatial information is not the most relevant !
  • 40.
    Before we startmaps Networks Références A CASE STUDY : ELECTIONS Maybe spatial information is not the most relevant !
  • 41.
    Before we startmaps Networks Références A CASE STUDY : ELECTIONS Or if really geography matters (2004 campaign) : From Andrew Gelman’s Blog. Each pixel represents 1,000 votes.
  • 42.
    Before we startmaps Networks Références GEOGRAPHY EXISTS IN THE DATA, BUT IS NOT THE MATTER OF COMPARISON
  • 43.
    Before we startmaps Networks Références ANOTHER GOOD EXAMPLE FOR NOT USING A MAP From Our World in Data
  • 44.
    Before we startmaps Networks Références EXAMPLES OF MAPS MISSISSIPPI MEANDERS The interest here is to compare location, lines,
  • 45.
    Before we startmaps Networks Références AIR MAP OF THE WORLD (1943)
  • 46.
    Before we startmaps Networks Références THE LONDON COUNTY COUNCIL BOMB DAMAGE MAPS, 1939-1945
  • 47.
    Before we startmaps Networks Références AIR ROUTE MAPS : AARON KOBLIN
  • 48.
    Before we startmaps Networks Références PARTIAL CONCLUSION Maps are useful
  • 49.
    Before we startmaps Networks Références PARTIAL CONCLUSION Maps are useful There are rules (over representation of large area, colorpleth,etc..)
  • 50.
    Before we startmaps Networks Références PARTIAL CONCLUSION Maps are useful There are rules (over representation of large area, colorpleth,etc..) Statistical maps are difficult to built :
  • 51.
    Before we startmaps Networks Références PARTIAL CONCLUSION Maps are useful There are rules (over representation of large area, colorpleth,etc..) Statistical maps are difficult to built : How to show uncertainty on a map ?
  • 52.
    Before we startmaps Networks Références PARTIAL CONCLUSION Maps are useful There are rules (over representation of large area, colorpleth,etc..) Statistical maps are difficult to built : How to show uncertainty on a map ? How to show correlations on a map ?
  • 53.
    Before we startmaps Networks Références PARTIAL CONCLUSION Maps are useful There are rules (over representation of large area, colorpleth,etc..) Statistical maps are difficult to built : How to show uncertainty on a map ? How to show correlations on a map ? Comparisons are limited (only geographical)
  • 54.
    Before we startmaps Networks Références PARTIAL CONCLUSION Maps are useful There are rules (over representation of large area, colorpleth,etc..) Statistical maps are difficult to built : How to show uncertainty on a map ? How to show correlations on a map ? Comparisons are limited (only geographical) Maps can help select, or highlight other elements (see D3.js, dashboards, or GeoXP package)
  • 55.
    Before we startmaps Networks Références QUESTIONS ON NETWORKS : There are many challenges in statistical networks analysis : Statistics on networks are quite difficult to handle
  • 56.
    Before we startmaps Networks Références QUESTIONS ON NETWORKS : There are many challenges in statistical networks analysis : Statistics on networks are quite difficult to handle Many types of networks
  • 57.
    Before we startmaps Networks Références QUESTIONS ON NETWORKS : There are many challenges in statistical networks analysis : Statistics on networks are quite difficult to handle Many types of networks Questions related to networks are hard to state (fuzzy or unarticulated)
  • 58.
    Before we startmaps Networks Références QUESTIONS ON NETWORKS : There are many challenges in statistical networks analysis : Statistics on networks are quite difficult to handle Many types of networks Questions related to networks are hard to state (fuzzy or unarticulated) Visualizations are barely readable (decoding is hard !)
  • 59.
    Before we startmaps Networks Références IS THIS A NETWORK OR A MAP ?
  • 60.
    Before we startmaps Networks Références IS THIS A NETWORK OR A MAP ? This is a Map showing links (air connections) between geographical entities.
  • 61.
    Before we startmaps Networks Références IS THIS A NETWORK OR A MAP ? This is a Map showing links (air connections) between geographical entities. This is “a collection of interconnected things”, (Oxford Englis Dictionary)
  • 62.
    Before we startmaps Networks Références TYPES OF NETWORKS Adjacency Networks
  • 63.
    Before we startmaps Networks Références TYPES OF NETWORKS Adjacency Networks
  • 64.
    Before we startmaps Networks Références TYPES OF NETWORKS Adjacency Networks Bipartite Networks
  • 65.
    Before we startmaps Networks Références TYPES OF NETWORKS Adjacency Networks Bipartite Networks
  • 66.
    Before we startmaps Networks Références TYPES OF NETWORKS Adjacency Networks Bipartite Networks From bipartite, one can create adjacency
  • 67.
    Before we startmaps Networks Références TYPES OF NETWORKS Adjacency Networks Bipartite Networks From bipartite, one can create adjacency
  • 68.
    Before we startmaps Networks Références TYPES OF NETWORKS Adjacency Networks Bipartite Networks From bipartite, one can create adjacency From Heijmans et al. (2014), and Kolaczyk (2009)
  • 69.
    Before we startmaps Networks Références TYPES OF NETWORKS Undirected (A& B ’know each other’) and directed (A ’owe money to’ B)
  • 70.
    Before we startmaps Networks Références TYPES OF NETWORKS Undirected (A& B ’know each other’) and directed (A ’owe money to’ B)
  • 71.
    Before we startmaps Networks Références TYPES OF NETWORKS Undirected (A& B ’know each other’) and directed (A ’owe money to’ B) From Kolaczyk and Csárdi (2014)
  • 72.
    Before we startmaps Networks Références FAMILIES OF GRAPHS
  • 73.
    Before we startmaps Networks Références FAMILIES OF GRAPHS Complete (top left) ; ring (top right) ; tree (bottom left) ; and star (bottom right)
  • 74.
    Before we startmaps Networks Références FAMILIES OF GRAPHS Complete (top left) ; ring (top right) ; tree (bottom left) ; and star (bottom right) From Kolaczyk and Csárdi (2014)
  • 75.
    Before we startmaps Networks Références A CLASSICAL NETWORK EXAMPLE Relationships of all of Victor Hugo’s characters of "Les Miserables". Data composed of nodes (characters) + Links (strength of links) http://bl.ocks.org/mbostock/4062045
  • 76.
    Before we startmaps Networks Références A CLASSICAL NETWORK EXAMPLE Relationships of all of Victor Hugo’s characters of "Les Miserables". Data composed of nodes (characters) + Links (strength of links) Nodes can be coloured (information on characters) http://bl.ocks.org/mbostock/4062045
  • 77.
    Before we startmaps Networks Références A CLASSICAL NETWORK EXAMPLE Relationships of all of Victor Hugo’s characters of "Les Miserables". Data composed of nodes (characters) + Links (strength of links) Nodes can be coloured (information on characters) Force-directed graph http://bl.ocks.org/mbostock/4062045
  • 78.
    Before we startmaps Networks Références A CLASSICAL NETWORK EXAMPLE Relationships of all of Victor Hugo’s characters of "Les Miserables". Data composed of nodes (characters) + Links (strength of links) Nodes can be coloured (information on characters) Force-directed graph Here, done with d3.js http://bl.ocks.org/mbostock/4062045
  • 79.
    Before we startmaps Networks Références A CLASSICAL NETWORK EXAMPLE Relationships of all of Victor Hugo’s characters of "Les Miserables".
  • 80.
    Before we startmaps Networks Références A CLASSICAL NETWORK EXAMPLE What do we see ? An overview of problems : Not the same graph each time (nondeterminstic algorithm)
  • 81.
    Before we startmaps Networks Références A CLASSICAL NETWORK EXAMPLE What do we see ? An overview of problems : Not the same graph each time (nondeterminstic algorithm) Spacial position does not encode attributes (algorithm-driven)
  • 82.
    Before we startmaps Networks Références A CLASSICAL NETWORK EXAMPLE What do we see ? An overview of problems : Not the same graph each time (nondeterminstic algorithm) Spacial position does not encode attributes (algorithm-driven) Proximity (of nodes) sometimes meaningful sometimes arbitrary. Artefacts created (some nodes “pushed back”.)
  • 83.
    Before we startmaps Networks Références A CLASSICAL NETWORK EXAMPLE What do we see ? An overview of problems : Not the same graph each time (nondeterminstic algorithm) Spacial position does not encode attributes (algorithm-driven) Proximity (of nodes) sometimes meaningful sometimes arbitrary. Artefacts created (some nodes “pushed back”.) What can we learn ? What can we compare ?
  • 84.
    Before we startmaps Networks Références A CLASSICAL NETWORK EXAMPLE What do we see ? An overview of problems : Not the same graph each time (nondeterminstic algorithm) Spacial position does not encode attributes (algorithm-driven) Proximity (of nodes) sometimes meaningful sometimes arbitrary. Artefacts created (some nodes “pushed back”.) What can we learn ? What can we compare ? Alternative view with bezier http://bl.ocks.org/mbostock/4600693
  • 85.
    Before we startmaps Networks Références HOW DOES IT WORK ? A vast family of Force-directed placement network representation Placing nodes randomly (put colour on groups)
  • 86.
    Before we startmaps Networks Références HOW DOES IT WORK ? A vast family of Force-directed placement network representation Placing nodes randomly (put colour on groups) Iteratively refine location following “forces”
  • 87.
    Before we startmaps Networks Références HOW DOES IT WORK ? A vast family of Force-directed placement network representation Placing nodes randomly (put colour on groups) Iteratively refine location following “forces” Nodes have “repulsive forces” (like electrons)
  • 88.
    Before we startmaps Networks Références HOW DOES IT WORK ? A vast family of Force-directed placement network representation Placing nodes randomly (put colour on groups) Iteratively refine location following “forces” Nodes have “repulsive forces” (like electrons) Links are “springs” (strength proportional to nb of connections)
  • 89.
    Before we startmaps Networks Références HOW DOES IT WORK ? A vast family of Force-directed placement network representation Placing nodes randomly (put colour on groups) Iteratively refine location following “forces” Nodes have “repulsive forces” (like electrons) Links are “springs” (strength proportional to nb of connections) Apply “some other rules‘” (see next slides)
  • 90.
    Before we startmaps Networks Références HOW DOES IT WORK ? A vast family of Force-directed placement network representation Placing nodes randomly (put colour on groups) Iteratively refine location following “forces” Nodes have “repulsive forces” (like electrons) Links are “springs” (strength proportional to nb of connections) Apply “some other rules‘” (see next slides) Iterate (computationally demanding)
  • 91.
    Before we startmaps Networks Références HOW DOES IT WORK ? A vast family of Force-directed placement network representation Placing nodes randomly (put colour on groups) Iteratively refine location following “forces” Nodes have “repulsive forces” (like electrons) Links are “springs” (strength proportional to nb of connections) Apply “some other rules‘” (see next slides) Iterate (computationally demanding) Wait until it stabilizes (even on a local equilibrium)
  • 92.
    Before we startmaps Networks Références FORCE-DIRECTED GRAPHS : Physically-based model + aesthetic touch + fuzzy stuff... From Tunkelang (1998)
  • 93.
    Before we startmaps Networks Références RULES FOR “NODE-LINK” REPRESENTATIONS Node-links representation follow rules : General rules : From Katya Ognyanova (2015) and Bahoken et al. (2013)
  • 94.
    Before we startmaps Networks Références RULES FOR “NODE-LINK” REPRESENTATIONS Node-links representation follow rules : General rules : Most connected nodes in the center From Katya Ognyanova (2015) and Bahoken et al. (2013)
  • 95.
    Before we startmaps Networks Références RULES FOR “NODE-LINK” REPRESENTATIONS Node-links representation follow rules : General rules : Most connected nodes in the center Less connected nodes at the periphery From Katya Ognyanova (2015) and Bahoken et al. (2013)
  • 96.
    Before we startmaps Networks Références RULES FOR “NODE-LINK” REPRESENTATIONS Node-links representation follow rules : General rules : Most connected nodes in the center Less connected nodes at the periphery Layout aesthetics rules : From Katya Ognyanova (2015) and Bahoken et al. (2013)
  • 97.
    Before we startmaps Networks Références RULES FOR “NODE-LINK” REPRESENTATIONS Node-links representation follow rules : General rules : Most connected nodes in the center Less connected nodes at the periphery Layout aesthetics rules : Minimize edge crossing From Katya Ognyanova (2015) and Bahoken et al. (2013)
  • 98.
    Before we startmaps Networks Références RULES FOR “NODE-LINK” REPRESENTATIONS Node-links representation follow rules : General rules : Most connected nodes in the center Less connected nodes at the periphery Layout aesthetics rules : Minimize edge crossing Prevent overlap From Katya Ognyanova (2015) and Bahoken et al. (2013)
  • 99.
    Before we startmaps Networks Références RULES FOR “NODE-LINK” REPRESENTATIONS Node-links representation follow rules : General rules : Most connected nodes in the center Less connected nodes at the periphery Layout aesthetics rules : Minimize edge crossing Prevent overlap Symmetry From Katya Ognyanova (2015) and Bahoken et al. (2013)
  • 100.
    Before we startmaps Networks Références RULES FOR “NODE-LINK” REPRESENTATIONS Node-links representation follow rules : General rules : Most connected nodes in the center Less connected nodes at the periphery Layout aesthetics rules : Minimize edge crossing Prevent overlap Symmetry Uniform edge length From Katya Ognyanova (2015) and Bahoken et al. (2013)
  • 101.
    Before we startmaps Networks Références LAYOUT AESTHETICS From Katya Ognyanova (2015)
  • 102.
    Before we startmaps Networks Références A NOTE ON DATA : MATRIX From Katya Ognyanova (2015)
  • 103.
    Before we startmaps Networks Références A NOTE ON DATA : EDGE LIST From Katya Ognyanova (2015)
  • 104.
    Before we startmaps Networks Références A NOTE ON DATA : NODE LIST From Katya Ognyanova (2015)
  • 105.
    Before we startmaps Networks Références A NOTE ON DATA : NODE ATTRIBUTES From Katya Ognyanova (2015)
  • 106.
    Before we startmaps Networks Références ALTERNATIVE VIEW : ADJACENT MATRIX PLOT An adjacency matrix, where each cell ij represents an edge from vertex i to vertex j. Here, vertices represent characters in a book, while edges represent co-occurrence in a chapter. http://bost.ocks.org/mike/miserables/
  • 107.
    Before we startmaps Networks Références NETWORKS : ADJACENT MATRIX PLOT As in many example, sorting is very useful !
  • 108.
    Before we startmaps Networks Références NETWORKS : ADJACENT MATRIX PLOT Adjacent matrix help identifying patterns From McGuffin (2012)
  • 109.
    Before we startmaps Networks Références NETWORKS : ARC DIAGRAM PLOT To put some structure in the graph : Horizontal alignment From Gaston Sanchez see also McGuffin (2012)
  • 110.
    Before we startmaps Networks Références NETWORKS : ARC DIAGRAM PLOT Now we can sort ! (according to groups, and then degrees) FromGaston Sanchez
  • 111.
    Before we startmaps Networks Références NETWORKS : ARC DIAGRAM PLOT : MY TOUCH !
  • 112.
    Before we startmaps Networks Références NETWORKS : ROLE OF TOPOLOGY Circular layouts of a 43-node, 80-edge network. Force-directed graph From McGuffin (2012)
  • 113.
    Before we startmaps Networks Références NETWORKS : ADDING A TOPOLOGY HELPS Circular layouts of a 43-node, 80-edge network. No ordering, with curved edges. From McGuffin (2012)
  • 114.
    Before we startmaps Networks Références NETWORKS : ADDING A TOPOLOGY HELPS Circular layouts of a 43-node, 80-edge network. Barycenter ordering, with curved edges.
  • 115.
    Before we startmaps Networks Références PROBLEM 1 : IDENTIFY REFERENCE GRAPHS Random Graphs difficult to identify
  • 116.
    Before we startmaps Networks Références PROBLEM 1 : IDENTIFY REFERENCE GRAPHS Random Graphs difficult to identify
  • 117.
    Before we startmaps Networks Références PROBLEM 1 : IDENTIFY REFERENCE GRAPHS Random Graphs difficult to identify Or
  • 118.
    Before we startmaps Networks Références PROBLEM 1 : IDENTIFY REFERENCE GRAPHS Random Graphs difficult to identify Or
  • 119.
    Before we startmaps Networks Références PROBLEM 1 : IDENTIFY REFERENCE GRAPHS Random Graphs difficult to identify Or → How to do any visual test ?
  • 120.
    Before we startmaps Networks Références PROBLEM 2 : LAYOUT CHANGE PERCEPTION Three layouts of the same graph From Kolaczyk and Csárdi (2014)
  • 121.
    Before we startmaps Networks Références PROBLEM 2 : LAYOUT CHANGE PERCEPTION Three layouts of the same graph From Kolaczyk and Csárdi (2014)
  • 122.
    Before we startmaps Networks Références PROBLEM 2 : LAYOUT CHANGE PERCEPTION Three layouts of the same graph From Kolaczyk and Csárdi (2014)
  • 123.
    Before we startmaps Networks Références PROBLEM 2 : LAYOUT CHANGE PERCEPTION Three layouts of the same graph → Circular, radial, layered. From Kolaczyk and Csárdi (2014)
  • 124.
    Before we startmaps Networks Références PROBLEM 3 : DECORATION HELPS ? From Kolaczyk and Csárdi (2014)
  • 125.
    Before we startmaps Networks Références PROBLEM 3 : DECORATION HELPS ? Plain and decorated visualizations of a karate club network From Kolaczyk and Csárdi (2014)
  • 126.
    Before we startmaps Networks Références PROBLEM 4 : SCALABILITY ? (192 blogs linked by 1,431 edges indicating at least one of the two blogs referenced the other). From Kolaczyk and Csárdi (2014)
  • 127.
    Before we startmaps Networks Références PROBLEM 4 : SCALABILITY ? French political blog network (192 blogs linked by 1,431 edges indicating at least one of the two blogs referenced the other). From Kolaczyk and Csárdi (2014)
  • 128.
    Before we startmaps Networks Références PROBLEM 4 : SCALABILITY ? French political blog network Towards an "hairball" + complexity is O(N2 v) (192 blogs linked by 1,431 edges indicating at least one of the two blogs referenced the other). From Kolaczyk and Csárdi (2014)
  • 129.
    Before we startmaps Networks Références SOLUTIONS : SPLIT ? From Kolaczyk and Csárdi (2014)
  • 130.
    Before we startmaps Networks Références SOLUTIONS : SPLIT ? Two ego-centric views of the karate club network From Kolaczyk and Csárdi (2014)
  • 131.
    Before we startmaps Networks Références SOLUTIONS : AGGREGATE ? From Kolaczyk and Csárdi (2014)
  • 132.
    Before we startmaps Networks Références SOLUTIONS : AGGREGATE ? French political blog network at the level of political parties From Kolaczyk and Csárdi (2014)
  • 133.
    Before we startmaps Networks Références REFERENCES I Bahoken, F., Beauguitte, L., and Lhomme, S. (2013). La visualisation des réseaux. principes, enjeux et perspectives. Bertin, J. (1981). Théorie matricielle de la graphique. Communication et langages, 48(1) :62–74. Buja, A., Cook, D., Hofmann, H., Lawrence, M., Lee, E.-K., Swayne, D. F., and Wickham, H. (2009). Statistical inference for exploratory data analysis and model diagnostics. Philosophical Transactions of the Royal Society of London A : Mathematical, Physical and Engineering Sciences, 367(1906) :4361–4383. Gelman, A. (2004). Exploratory data analysis for complex models. Journal of Computational and Graphical Statistics, 13(4). Heijmans, R., Heuver, R., Levallois, C., and Lelyveld, I. V. (2014). Dynamic visualization of large transaction networks : the daily dutch overnight money market. Kolaczyk, E. D. (2009). Statistical Analysis of Network Data : Methods and Models. Springer Series in Statistics. Springer-Verlag New York, 1 edition. Kolaczyk, E. D. and Csárdi, G. (2014). Statistical Analysis of Network Data with R. Use R ! 65. Springer-Verlag New York, 1 edition.
  • 134.
    Before we startmaps Networks Références REFERENCES II McGuffin, M. J. (2012). Simple algorithms for network visualization : A tutorial. Tsinghua Science and Technology, 17(4) :383–398. Ognyanova, K. (2015). R network visualization workshop. In POLNET 2015, Portland OR. Tufte, E. R. (2001). The Visual Display of Quantitative Information. Graphics Press, 2 edition. Tunkelang, D. (1998). A Numerical Optimization Approach to Graph Drawing. PhD thesis, Dissertation, Carnegie Mellon University, School of Computer Science.