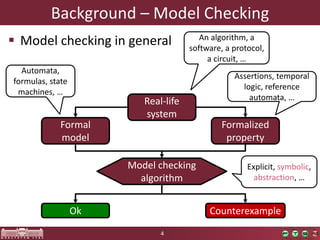
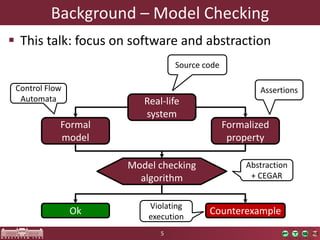
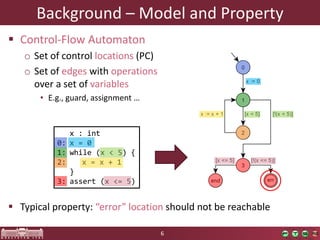
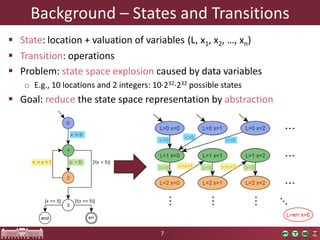
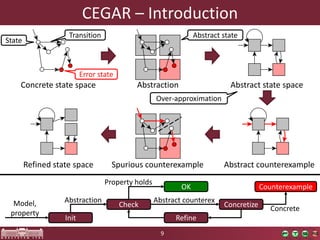
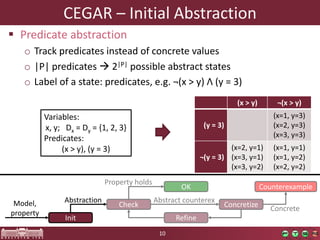
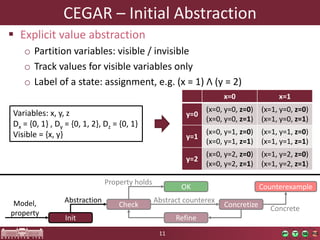
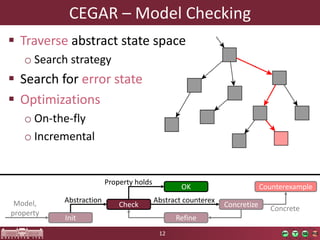
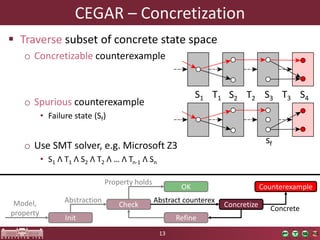
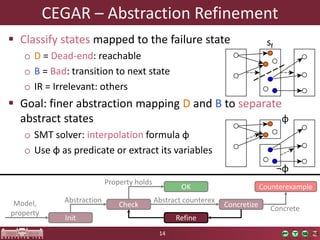
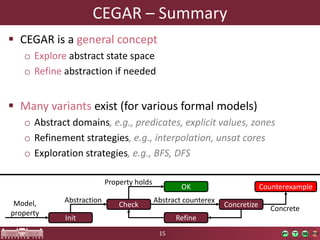
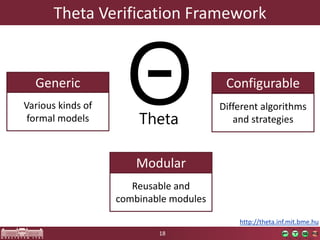
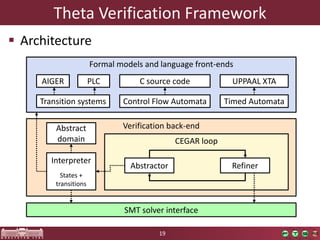
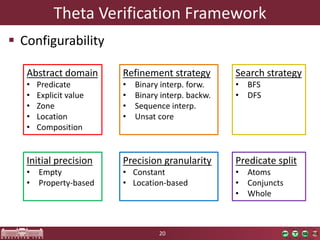
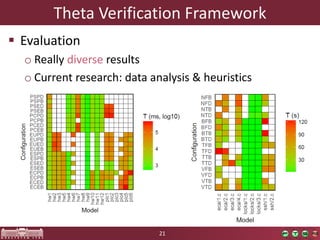
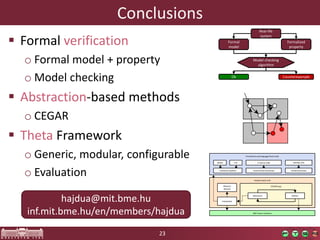
This document discusses abstraction-based software verification using Counterexample-Guided Abstraction Refinement (CEGAR). CEGAR iteratively refines an abstract model of the software by analyzing counterexamples generated from model checking the abstract model against a property. The document introduces CEGAR and describes how it uses abstraction, model checking, concretization, and refinement. It also discusses the Theta Verification Framework, a configurable CEGAR framework that can handle different formal models, abstract domains, and refinement strategies.

1. 1
Budapest University of Technology and Economics
Department of Measurement and Information Systems
Software Verification with
Abstraction-Based Methods
Ákos Hajdu
PhD student
Department of Measurement and Information Systems, Budapest University of Technology and Economics
MTA-BME Lendület Cyber-Physical Systems Research Group
Electrical and Computer Engineering Department, McGill University

2. 2
Background

3. 3
Background – Formal Verification
 Formal verification
o Prove or disprove the correctness of a system with
respect to a formal property (specification) relying
on sound mathematical basis
 Model checking
o Exhaustively enumerate the possible states and
transitions (the state space) of the system and
check if it meets the property

4. 4
Background – Model Checking
 Model checking in general
Formal
model
Formalized
property
Model checking
algorithm
Ok Counterexample
Real-life
system
An algorithm, a
software, a protocol,
a circuit, …
Automata,
formulas, state
machines, …
Assertions, temporal
logic, reference
automata, …
Explicit, symbolic,
abstraction, …

5. 5
Background – Model Checking
 This talk: focus on software and abstraction
Formal
model
Formalized
property
Model checking
algorithm
Ok Counterexample
Real-life
system
Source code
Control Flow
Automata
Assertions
Abstraction
+ CEGAR
Violating
execution

6. 6
Background – Model and Property
 Control-Flow Automaton
o Set of control locations (PC)
o Set of edges with operations
over a set of variables
• E.g., guard, assignment …
 Typical property: “error” location should not be reachable
x : int
0: x = 0
1: while (x < 5) {
2: x = x + 1
}
3: assert (x <= 5)

7. 7
Background – States and Transitions
 State: location + valuation of variables (L, x1, x2, …, xn)
 Transition: operations
 Problem: state space explosion caused by data variables
o E.g., 10 locations and 2 integers: 10·232·232 possible states
 Goal: reduce the state space representation by abstraction

8. 8
Counterexample-Guided
Abstraction Refinement (CEGAR)

9. 9
CEGAR – Introduction
Concrete state space Abstraction Abstract state space
Abstract counterexampleSpurious counterexampleRefined state space
Init
Check
OK
Concretize
Counterexample
Refine
Model,
property
Abstraction
Property holds
Abstract counterex
Concrete
State
Transition
Error state
Abstract state
Over-approximation

10. 10
ConcretizeCheck
OK Counterexample
Refine
Property holds
Abstract counterex
Concrete
CEGAR – Initial Abstraction
 Predicate abstraction
o Track predicates instead of concrete values
o |P| predicates  2|P| possible abstract states
o Label of a state: predicates, e.g. ¬(x > y) Ʌ (y = 3)
(x > y) ¬(x > y)
(y = 3)
(x=1, y=3)
(x=2, y=3)
(x=3, y=3)
¬(y = 3)
(x=2, y=1)
(x=3, y=1)
(x=3, y=2)
(x=1, y=1)
(x=1, y=2)
(x=2, y=2)
Variables:
x, y; Dx = Dy = {1, 2, 3}
Predicates:
(x > y), (y = 3)
Init
Model,
property
Abstraction

11. 11
Refine
Counterexample
ConcreteConcretize
Abstract counterex
OK
Property holds
Check
CEGAR – Initial Abstraction
 Explicit value abstraction
o Partition variables: visible / invisible
o Track values for visible variables only
o Label of a state: assignment, e.g. (x = 1) Ʌ (y = 2)
Variables: x, y, z
Dx = {0, 1} , Dy = {0, 1, 2}, Dz = {0, 1}
Visible = {x, y}
x=0 x=1
y=0
(x=0, y=0, z=0)
(x=0, y=0, z=1)
(x=1, y=0, z=0)
(x=1, y=0, z=1)
y=1
(x=0, y=1, z=0)
(x=0, y=1, z=1)
(x=1, y=1, z=0)
(x=1, y=1, z=1)
y=2
(x=0, y=2, z=0)
(x=0, y=2, z=1)
(x=1, y=2, z=0)
(x=1, y=2, z=1)
Init
Model,
property
Abstraction

12. 12
Refine
Counterexample
ConcreteConcretize
Init
Model,
property
CEGAR – Model Checking
 Traverse abstract state space
o Search strategy
 Search for error state
 Optimizations
o On-the-fly
o Incremental
Check
OK
Abstraction
Property holds
Abstract counterex

13. 13
Refine
OK
Property holds
Check
Abstraction
Init
Model,
property
CEGAR – Concretization
 Traverse subset of concrete state space
o Concretizable counterexample
o Spurious counterexample
• Failure state (Sf)
o Use SMT solver, e.g. Microsoft Z3
• S1 Ʌ T1 Ʌ S2 Ʌ T2 Ʌ … Ʌ Tn-1 Ʌ Sn
sf
Concretize
Counterexample
Abstract counterex
Concrete
S1 S2 S3 S4T1 T2 T3

14. 14
Counterexample
ConcreteConcretize
Abstract counterex
OK
Property holds
Check
Abstraction
Init
Model,
property
CEGAR – Abstraction Refinement
 Classify states mapped to the failure state
o D = Dead-end: reachable
o B = Bad: transition to next state
o IR = Irrelevant: others
 Goal: finer abstraction mapping D and B to separate
abstract states
o SMT solver: interpolation formula φ
o Use φ as predicate or extract its variables
Refine
φ
¬φ
sf

15. 15
CEGAR – Summary
 CEGAR is a general concept
o Explore abstract state space
o Refine abstraction if needed
 Many variants exist (for various formal models)
o Abstract domains, e.g., predicates, explicit values, zones
o Refinement strategies, e.g., interpolation, unsat cores
o Exploration strategies, e.g., BFS, DFS
Counterexample
ConcreteConcretize
Abstract counterex
OK
Property holds
Check
Abstraction
Init
Model,
property
Refine

16. 16
Research Questions
 Integrate variants into common framework? Combine?
o Theta Verification Framework. http://theta.inf.mit.bme.hu
o A configurable CEGAR framework with interpolation-based refinements. Ákos Hajdu,
Tamás Tóth, András Vörös, and István Majzik. FORTE 2016, vol. 9688 of LNCS.
 Which variants perform well for given verification tasks?
o Exploratory analysis of the performance of a configurable CEGAR framework. Ákos
Hajdu and Zoltán Micskei. PhD Mini-Symposium 2017, BME DMIS.
o Towards evaluating size reduction techniques for software model checking. Gyula
Sallai, Ákos Hajdu, Tamás Tóth, and Zoltán Micskei. VPT 2017. (Accepted)
 Domain specific CEGAR variants?
o Exploiting hierarchy in the abstraction-based verification of statecharts using SMT
solvers. Bence Czipó, Ákos Hajdu, Tamás Tóth, and István Majzik. FESCA 2017, vol.
245 of EPTCS.
o New search strategies for the Petri net CEGAR approach. Ákos Hajdu, András Vörös,
and Tamás Bartha. ICATPN 2015, vol. 9115 of LNCS.
http://home.mit.bme.hu/~hajdua/publications

17. 17
Theta Verification Framework

18. 18
Theta Verification Framework
ΘTheta
Generic
Various kinds of
formal models
Modular
Reusable and
combinable modules
Configurable
Different algorithms
and strategies
http://theta.inf.mit.bme.hu

19. 19
Formal models and language front-ends
Theta Verification Framework
 Architecture
Transition systems Control Flow Automata Timed Automata
C source code UPPAAL XTAAIGER PLC
Verification back-end
SMT solver interface
Abstract
domain
Interpreter
States +
transitions
CEGAR loop
Abstractor Refiner

20. 20
Theta Verification Framework
 Configurability
Abstract domain
• Predicate
• Explicit value
• Zone
• Location
• Composition
Refinement strategy
• Binary interp. forw.
• Binary interp. backw.
• Sequence interp.
• Unsat core
Search strategy
• BFS
• DFS
Initial precision
• Empty
• Property-based
Precision granularity
• Constant
• Location-based
Predicate split
• Atoms
• Conjuncts
• Whole

21. 21
Theta Verification Framework
 Evaluation
o Really diverse results
o Current research: data analysis & heuristics

22. 22
Conclusions

23. 23
Conclusions
 Formal verification
o Formal model + property
o Model checking
 Abstraction-based methods
o CEGAR
 Theta Framework
o Generic, modular, configurable
o Evaluation
hajdua@mit.bme.hu
inf.mit.bme.hu/en/members/hajdua
Formal
model
Formalized
property
Model checking
algorithm
Ok Counterexample
Real-life
system
Formalisms and language front-ends
Transition systems Control Flow Automata Timed Automata
C source code UPPAAL XTAAIGER PLC
Analysis back-end
SMT solver interface
Abstract
domain
Interpreter
CEGAR loop
Abstractor Refiner