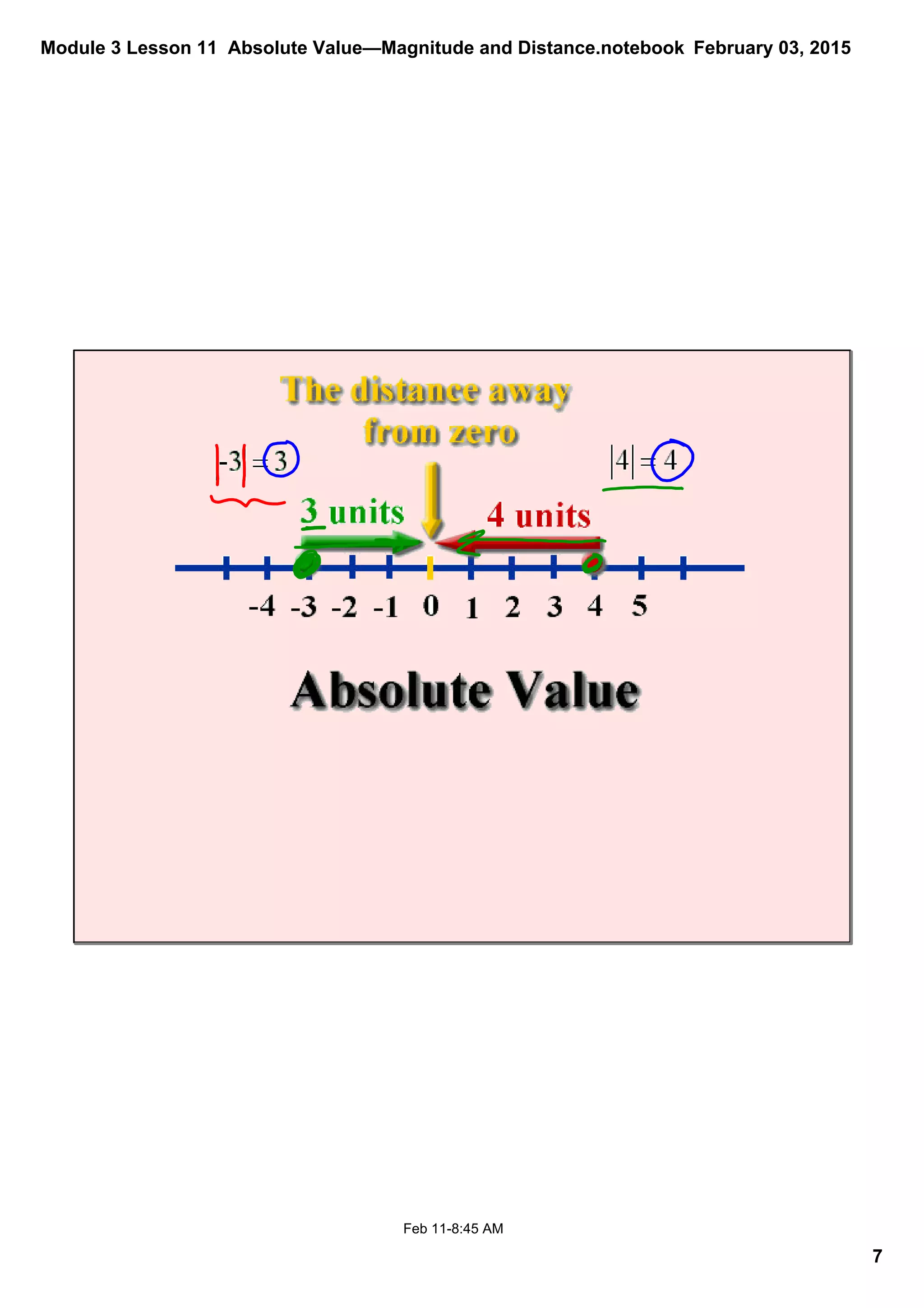
This document discusses absolute value and its uses. It begins with examples of absolute value as the distance between numbers and zero on the number line. Students then work through exercises calculating absolute values and using absolute value to find the magnitude, or size, of quantities in real-world contexts like temperatures, debts, and weights. The document ensures students understand that absolute value is never negative, as it represents distance or magnitude. It poses discussion questions at the end to check understanding of key absolute value concepts.