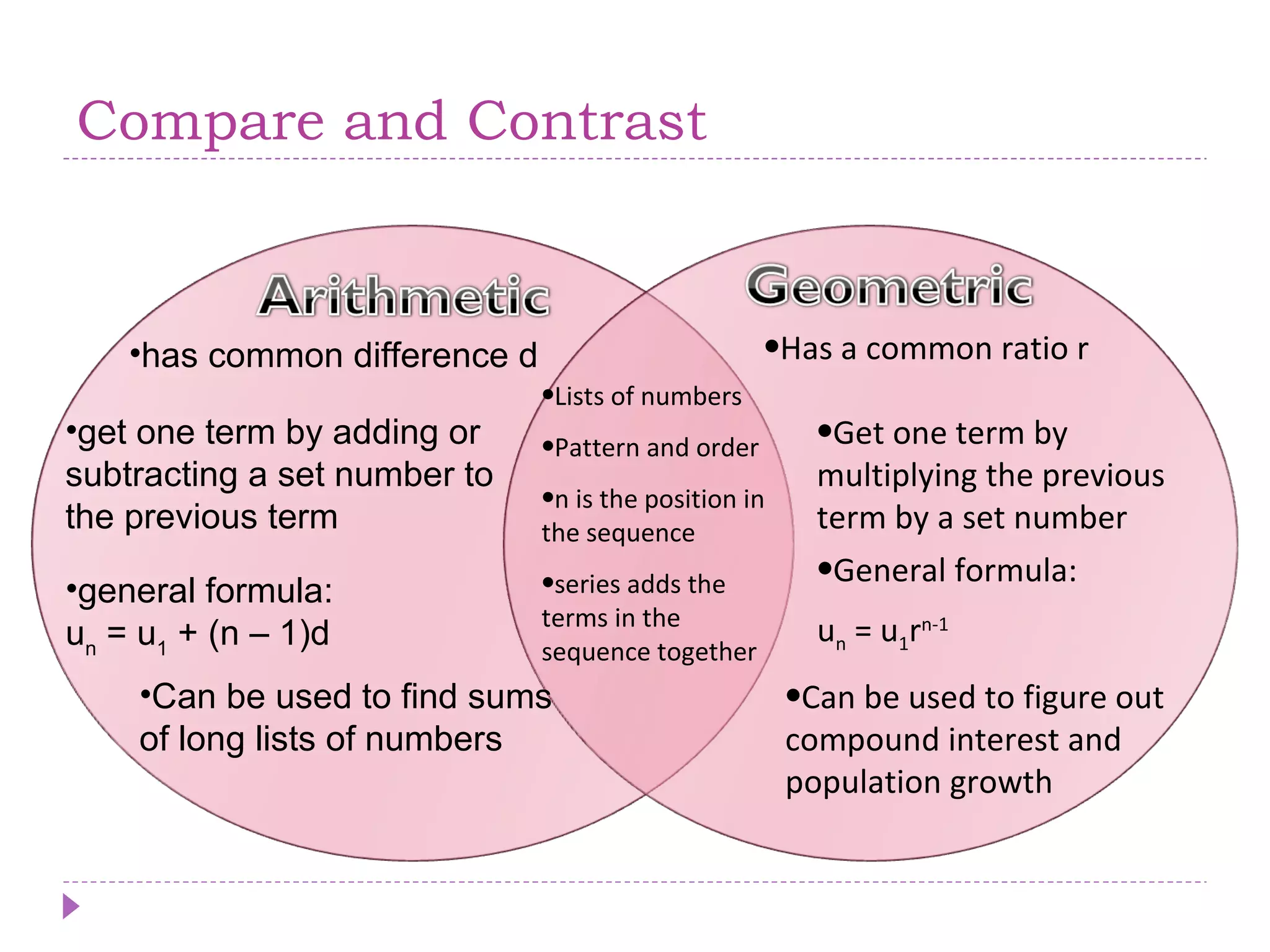
The document discusses arithmetic and geometric sequences and series. It provides examples of different sequences and explains how to determine the general formulas for finding any term in the sequence. Specifically, it explains that arithmetic sequences have a common difference and use the formula un = u1 + (n-1)d, while geometric sequences have a common ratio and use the formula un = u1rn-1. It also discusses how series are used to sum the terms of sequences and provides examples of applications for arithmetic and geometric sequences/series such as solving math problems, determining total costs or earnings, and calculating compound interest or population growth.

1. Sequences …and Series Exploring Arithmetic and Geometric Sequences

2. Sequences 1, 2, 3, 4, 5, 6, 7, … 1, 3, 5, 7, 9, 11, … 2, 4, 8, 16, 32, 64, … 1, 1, 2, 3, 5, 8, 13, 21, … 27, 20, 13, 6, -1, -8, … 40, 20, 10, 5, 2.5, 1.25, … 3, 9, 27, 81, 243, 729, …

3. Arithmetic Sequences Ex.1) 2, 5, 8, 11, 14, 17, 20, … Ex. 2) 4, 9, 14, 19, 24, 29, 34, … Ex. 3) 1, 8, 15, 22, 29, 36, … Notes: Lists of Numbers Pattern Set difference between terms

4. Generalizing Arithmetic Sequences Ex.1) 2, 5, 8, 11, 14, 17, 20, … 5 – 2 = 3, 8 – 5 = 3, 11 – 8 = 3 … 20 – 17 = 3 Difference = 3 = d (2 + 3) = u 2 , (5 + 3) = u 3 , (u 2 + 3) = u 3 (2 + 3 + 3) = u 3 , 2 + 2(3) = u 3 , 2 = 3 – 1 u n = (2 + 3(n – 1)) Ex. 3) 1, 8, 15, 22, 29, 36, … 8 – 1 = 7, 15 – 8 = 7, 22 – 15 = 7 … 36 – 29 = 7 d = 7 (1 + 7) = u 2 , (8 + 7) = u 3 (1 + 7 + 7) = u 3 , 1 + 2(7) = u 3 , 2 = 3 – 1 u n = (1 + 7(n – 1)) Notes: Determine common difference General formula: u n = u 1 + (n – 1)d

5. Geometric Sequences Ex. 1) 2, 4, 8, 16, 32, 64, … Ex. 2) 1000,100, 10, 1, 0.1, 0.01, … Ex.3) 3, 9, 27, 81, 243, 729, … Notes: List of numbers Pattern [Multiplication] Common ratio [r]

6. Generalizing Geometric Sequences Ex. 1) 2, 4, 8, 16, 32, 64, … 4÷2 = 2, 8÷4 = 2, … 64÷32 = 2 Common ratio r = 2 u 1 ×2 = u 2 , u 2 ×2 = u 3 , (u 1 ×2)×2 = u 3 u 3 = u 1 ×(2 2 ) , thus u n = u 1 (2 n-1 ) Ex. 2) 1000,100, 10, 1, 0.1, 0.01, … 100÷1000 = 1 / 10 , 10÷100 = 1 / 10 Common ratio r = 1 / 10 1 / 10 × u 1 = u 2 , 1 / 10 × u 2 = u 3 , 1 / 10 × ( 1 / 10 × u 1 )= u 3 u 3 = u 1 ×( 1 / 10 ) 2 , thus u n = u 1 ( 1 / 10 ) n-1 Notes: Find common ration r [dividing one term by previous term] General formula: u n = u 1 (r n-1 )

7. Series Arithmetic Series 2 + 5 + 8 + 11+ 14 +17 + 20 +… 4 + 9 +14 +19 + 24 + 29 + 34 +… Geometric Series 2 + 4 + 8 + 16 + 32 + 64… 3 + 9 + 27 + 81 + 243 + 729… What is a series? Lists of numbers with patterns Terms of sequences added together

8. Applications What are Arithmetic Sequences used for? Solving Math Problems Used in conjunction with Series [Arithmetic Series] Can be used to sum up long lists of numbers Can be used to sum up prices Ex. Theater tickets are sold for $60 for odd numbered tickets and $40 for even numbered tickets. There are 50 seats in the theater, how much money do even tickets bring in if all are sold? What are Geometric Sequences used for? Solving Compound Interest When money is put into a bank it gains a percentage interest. At any given point in time geometric series can determine how much money is in the bank, with interest. To calculate population growth, often in biology.

9. Recognizing Sequences 1, 2, 3, 4, 5, 6, 7, … 1, 3, 5, 7, 9, 11, … 2, 4, 8, 16, 32, 64, … 1, 1, 2, 3, 5, 8, 13, 21, … 27, 20, 13, 6, -1, -8, … 40, 20, 10, 5, 2.5, 1.25, … 3, 9, 27, 81, 243, 729, …

10. Properties Arithmetic Sequences Geometric Sequences A list of numbers There is a pattern and order Get one term by adding a number to the previous term in the sequence There is a common difference d n represents position in the list (nth term) General formula: u n =u 1 +(n-1)d Series adds each term in a sequence together Can be used to sum lists of numbers, cost and money A list of numbers There is a pattern and order Get one term by multiplying the previous term by a set number There is a common ratio r n represents position in the list (nth term) General formula: u n = u 1 r n-1 Series adds each term n a sequence together Can be used to determine growth, population growth and interest

11. Properties - Similarities Arithmetic Sequences Geometric Sequences A list of numbers There is a pattern and order Get one term by adding a number to the previous term in the sequence There is a common difference d n represents position in the list (nth term) General formula: u n =u 1 +(n-1)d Series adds each term in a sequence together Can be used to sum lists of numbers, cost and money A list of numbers There is a pattern and order Get one term by multiplying the previous term by a set number There is a common ratio r n represents position in the list (nth term) General formula: u n = u 1 r n-1 Series adds each term n a sequence together Can be used to determine growth, population growth and interest

12. Properties - Differences Arithmetic Sequences Geometric Sequences A list of numbers There is a pattern and order Get one term by adding a number to the previous term in the sequence A common difference d n represents position in the list (nth term) Gen. formula: u n =u 1 +(n-1)d Series adds each term in a sequence together Can be used to sum lists of numbers, cost and money A list of numbers There is a pattern and order Get one term by multiplying the previous term by a set number There is a common ratio r n represents position in the list (nth term) General formula: u n = u 1 r n-1 Series adds each term n a sequence together Can be used to determine growth, population growth and interest

13. Compare and Contrast Lists of numbers Pattern and order n is the position in the sequence series adds the terms in the sequence together has common difference d get one term by adding or subtracting a set number to the previous term general formula: u n = u 1 + (n – 1)d Can be used to find sums of long lists of numbers Has a common ratio r Get one term by multiplying the previous term by a set number General formula: u n = u 1 r n-1 Can be used to figure out compound interest and population growth

14. Now for Review Get into groups of four Review information presented in class Write helpful information on index cards [keep it on the lines – one side] 5 minutes