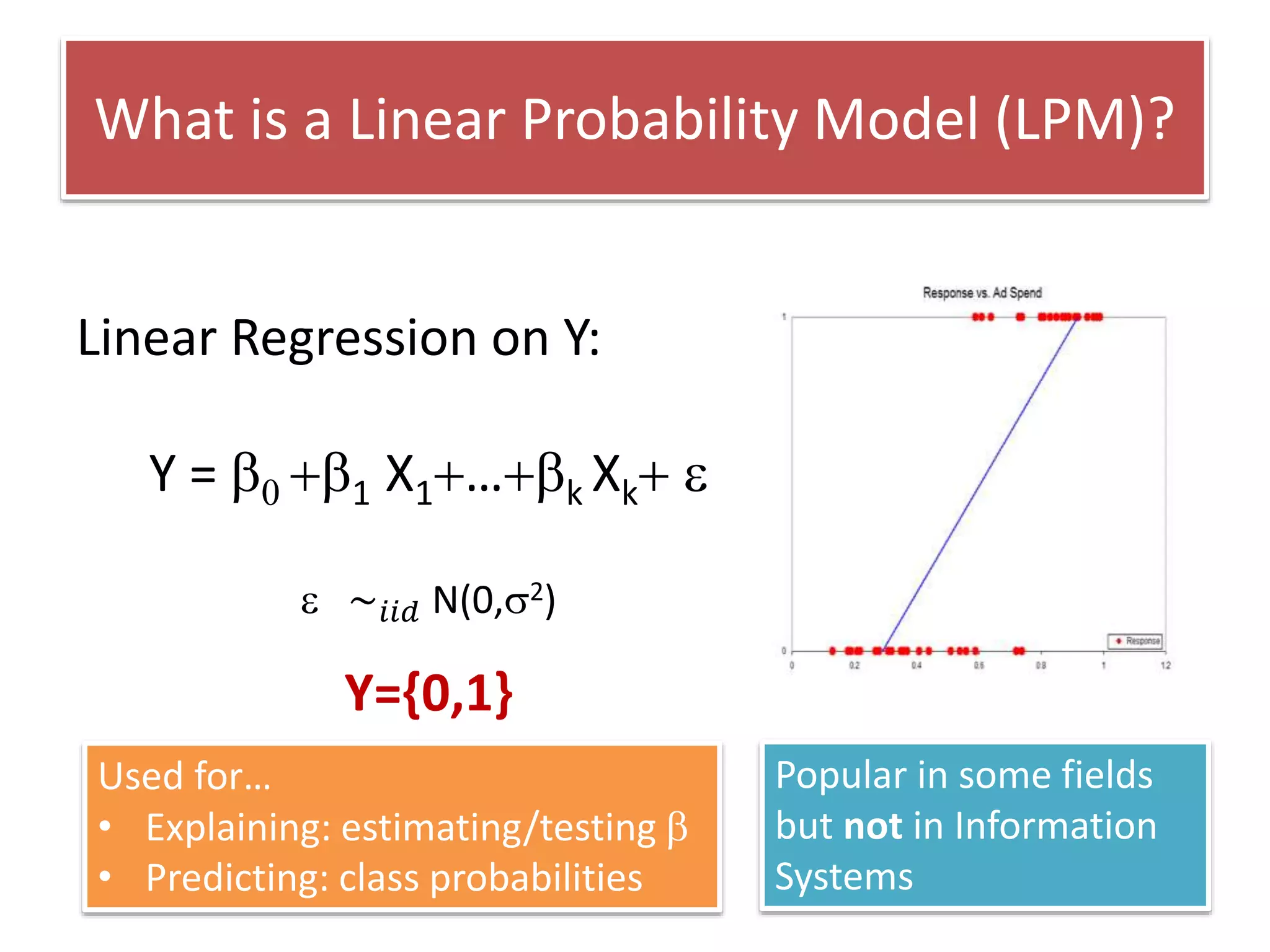
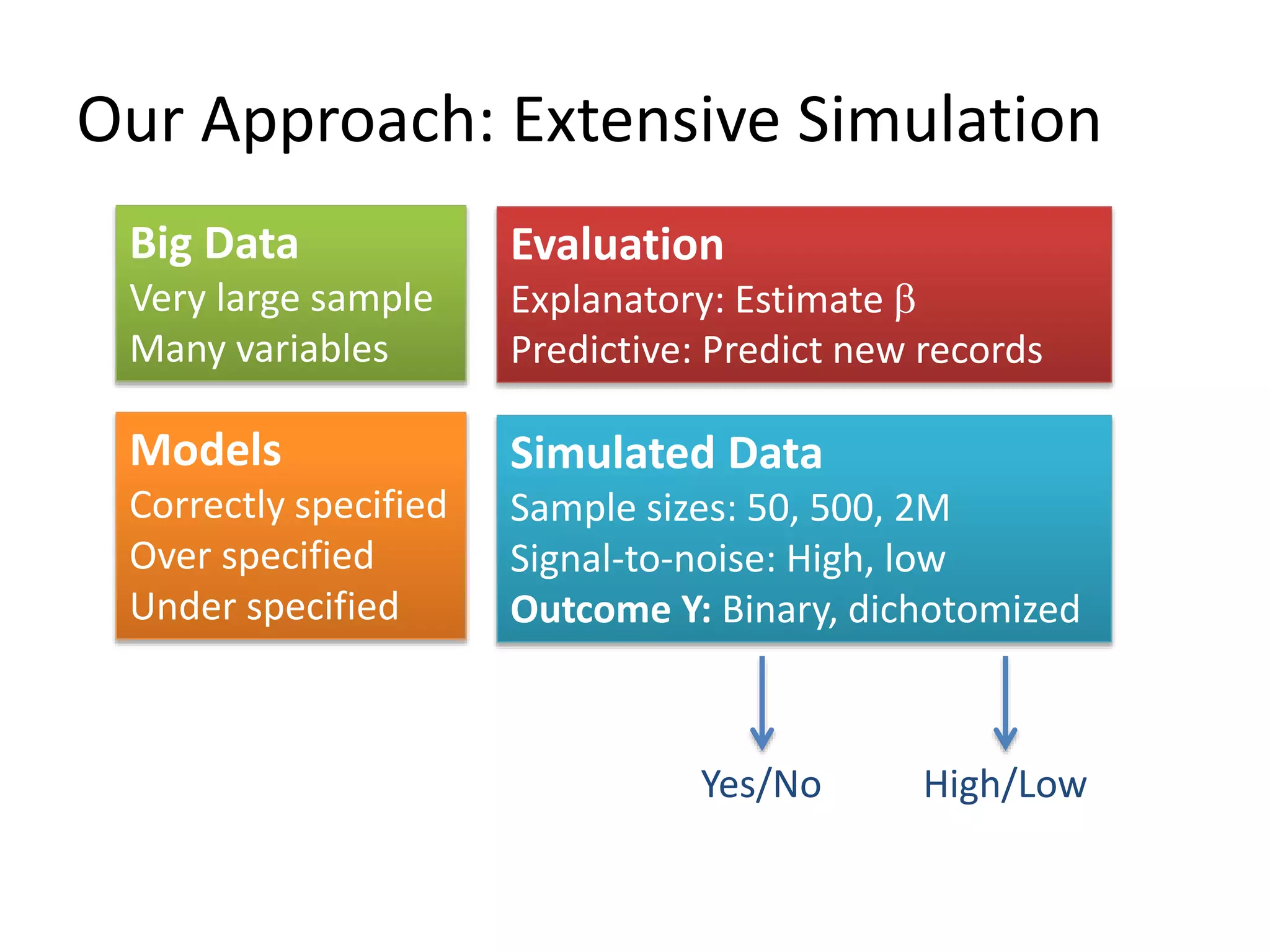
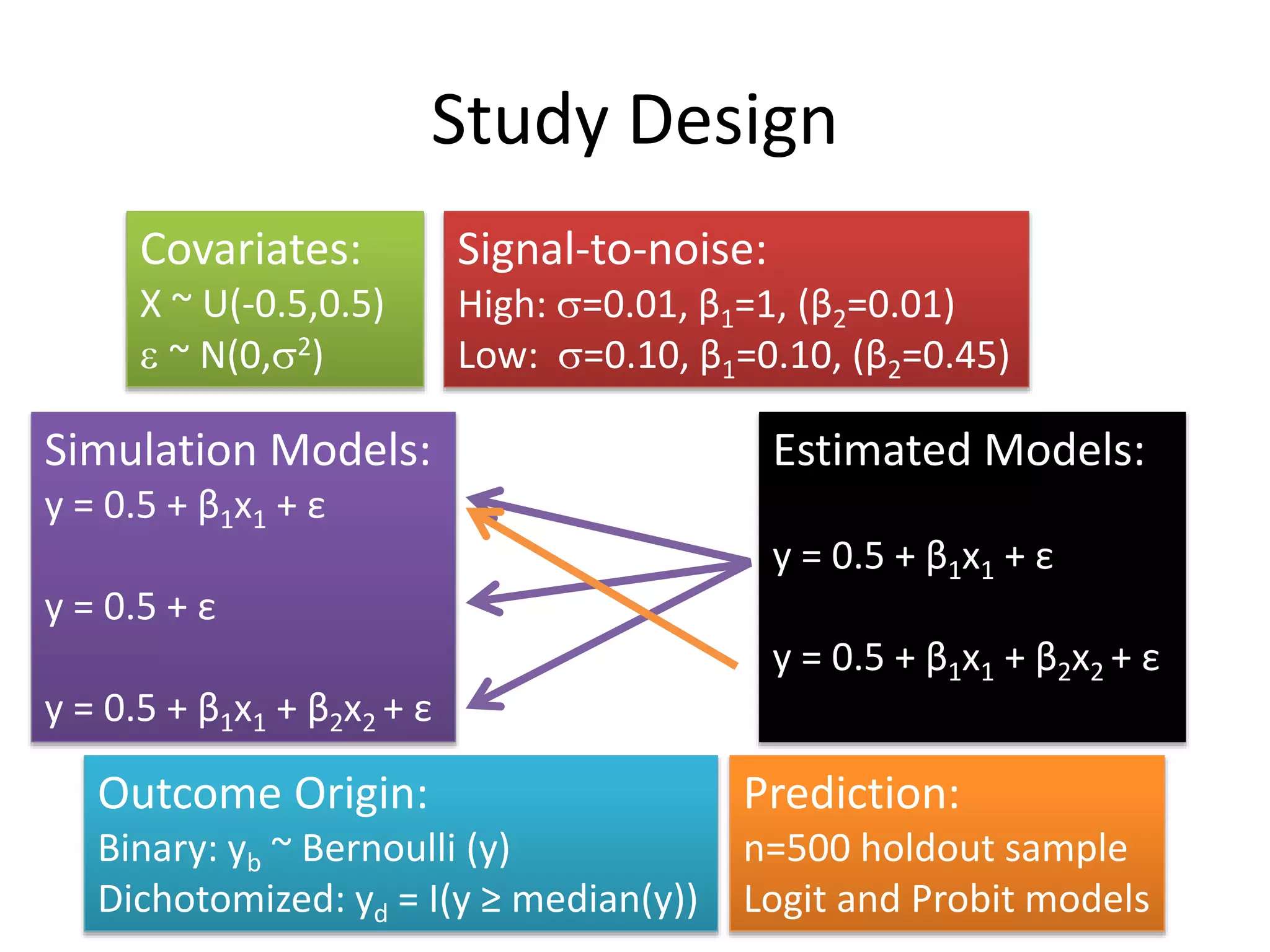
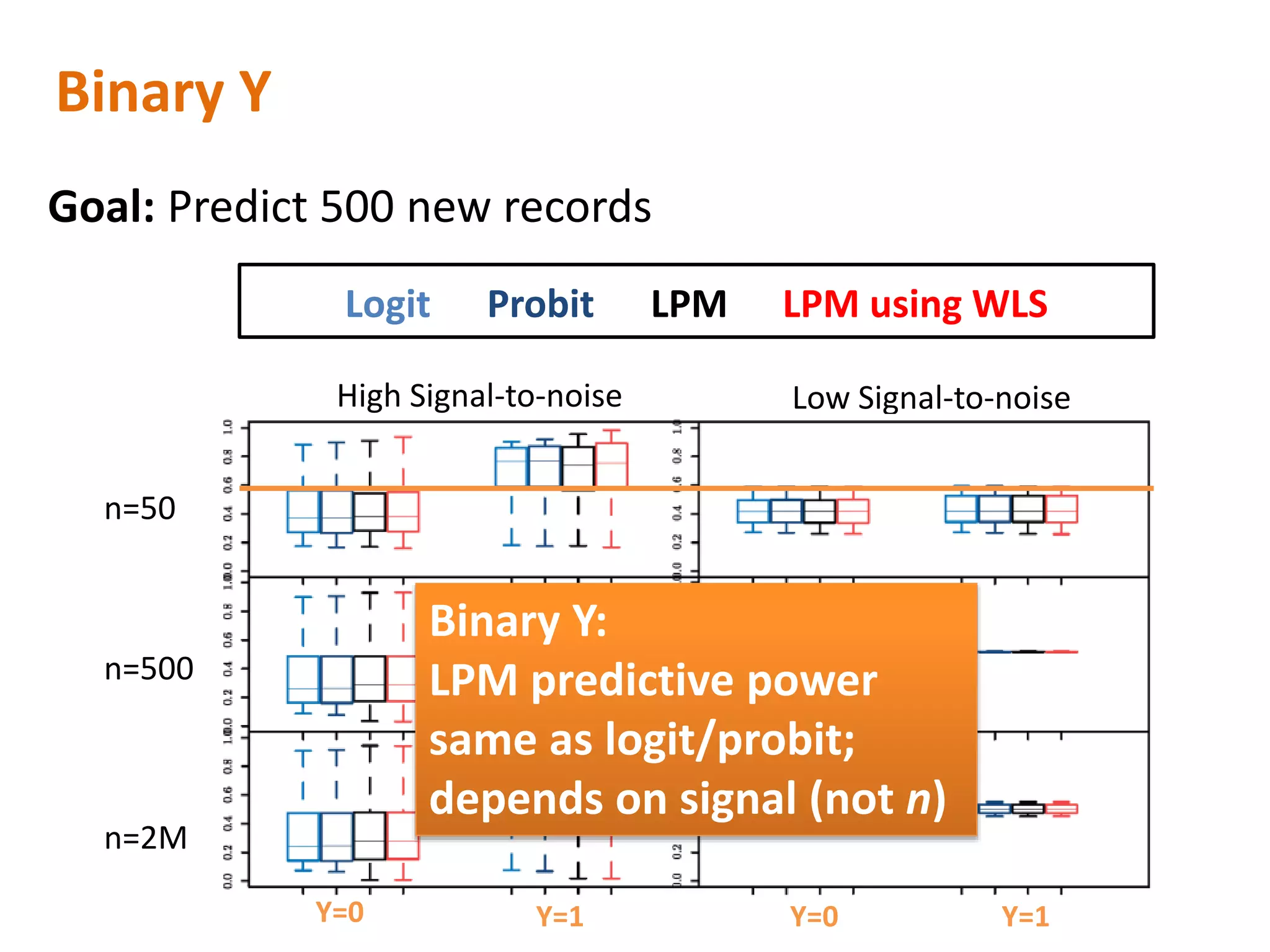
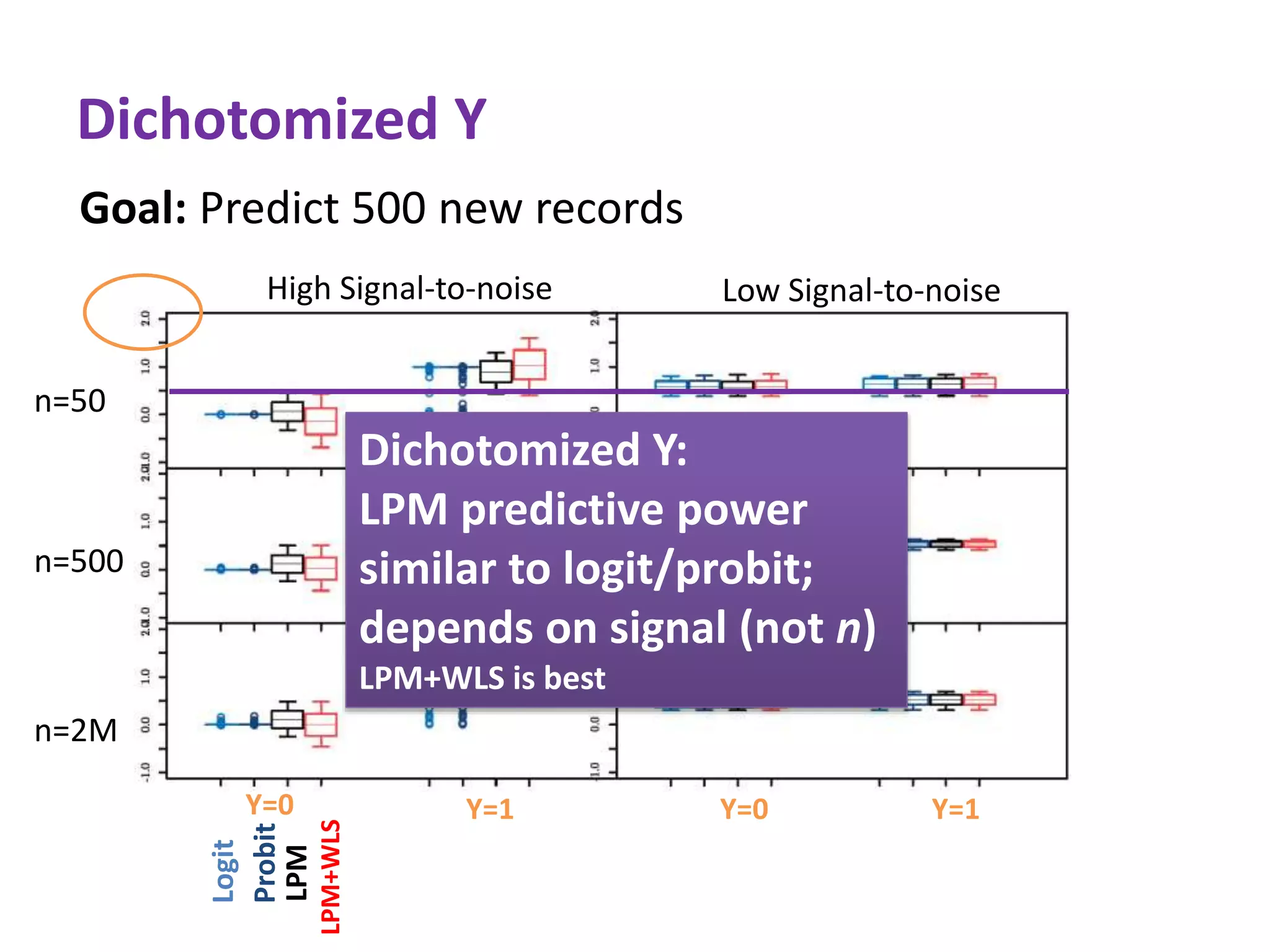
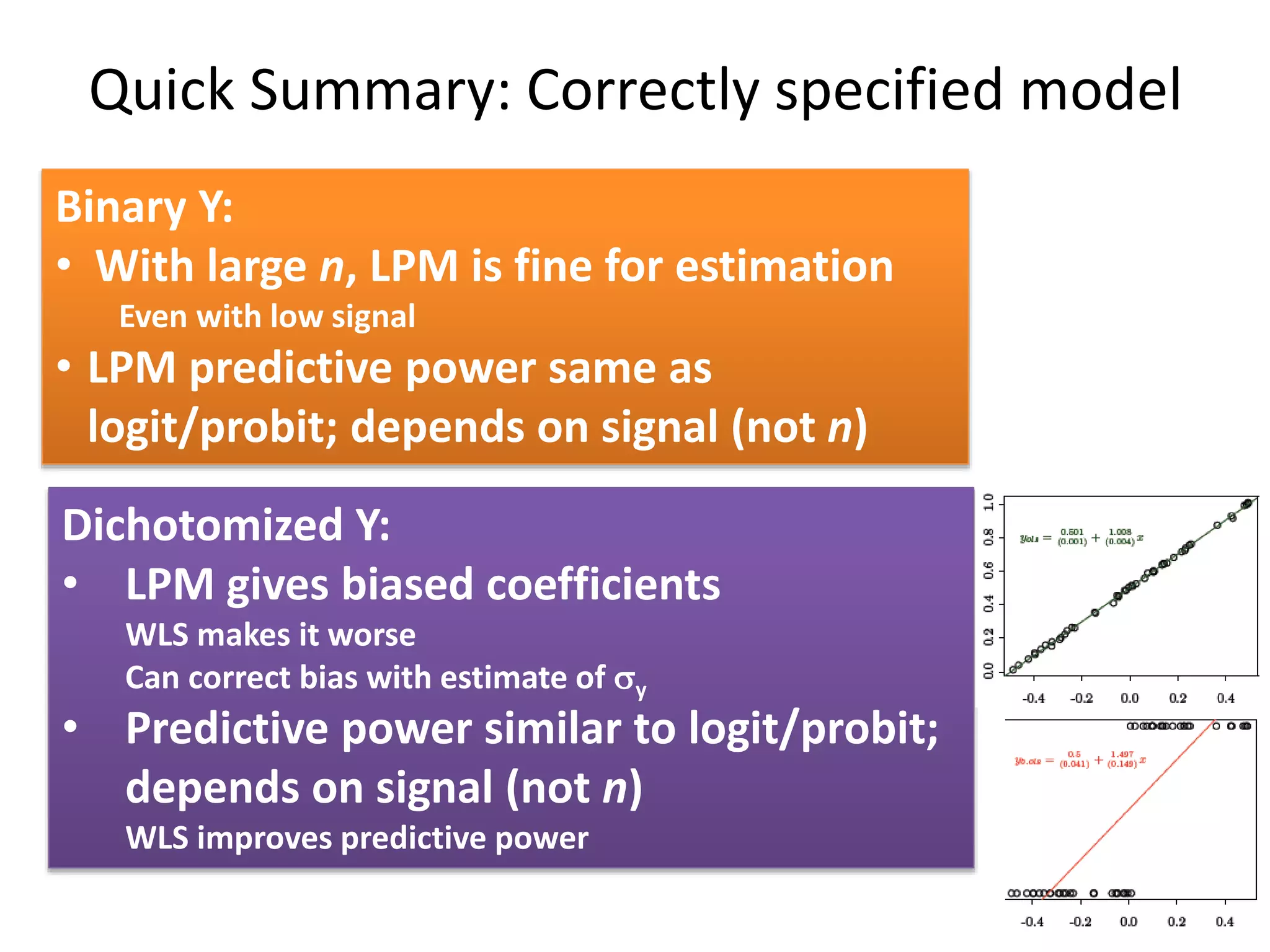
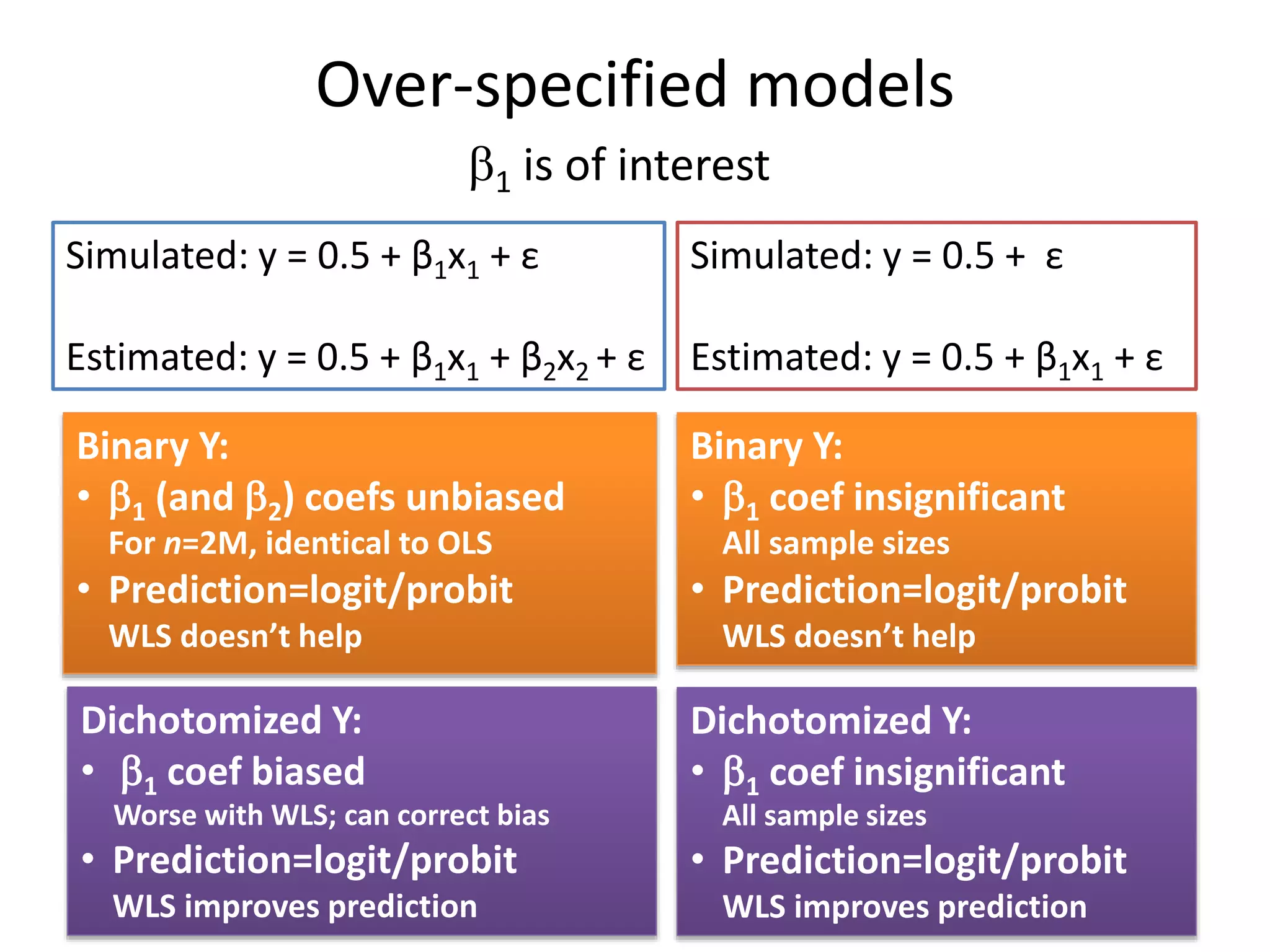
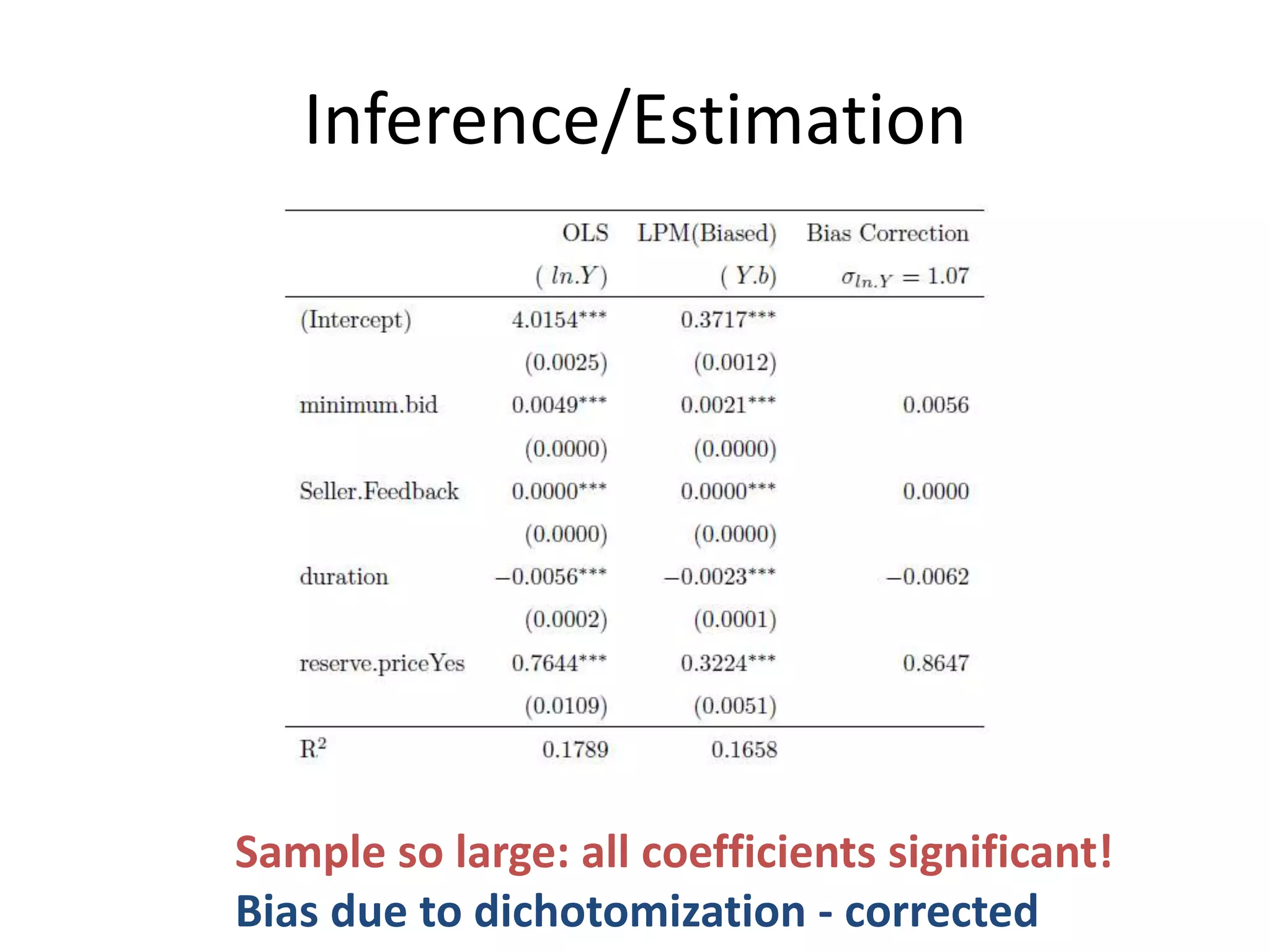
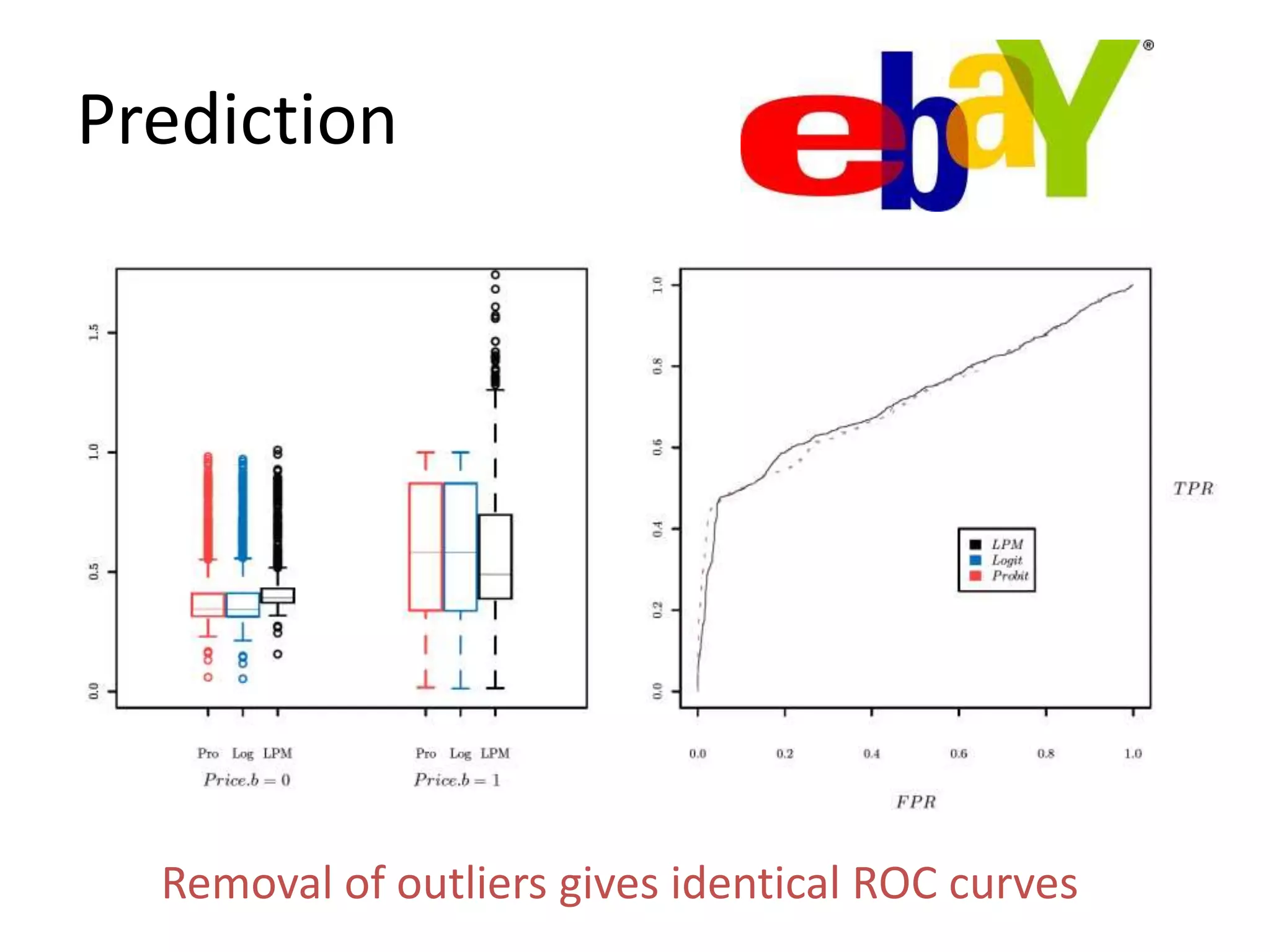
The document discusses the use of linear probability models (LPM) for binary outcomes, highlighting their simplicity and comparable predictive power to logistic/probit models despite frequent criticism. It presents a simulation study that evaluates LPM's effectiveness under varying conditions, revealing that large sample sizes can mitigate bias and yield satisfactory estimation results. The authors conclude that while LPM is rare in information systems, it can be a viable option in certain contexts, particularly with adequately large datasets.

1. Linear Probability Models and Big Data
Kosher or Not?
Galit Shmueli & Suneel Chatla

2. Linear Regression on Y:
Y = b0 +b1 X1+…+bk Xk+ e
e ~𝑖𝑖𝑑 N(0,s2)
Y={0,1}
What is a Linear Probability Model (LPM)?
Used for…
• Explaining: estimating/testing b
• Predicting: class probabilities
Popular in some fields
but not in Information
Systems

3. Criticism in the Literature e ~𝒊𝒊𝒅 N(0,s2)
Common advice: use logistic/probit model

4. Why do researchers still use LPM?
Compared to logit/probit:
• Easy coefficient interpretation
• Same statistical significance
• Works under quasi/full-separation
• Cheap computation
Relevant
for
InferenceRelevant
for
Prediction
LPM is rare in IS

5. Should we use LPM?

6. Our Approach: Extensive Simulation
Evaluation
Explanatory: Estimate b
Predictive: Predict new records
Big Data
Very large sample
Many variables
Models
Correctly specified
Over specified
Under specified
Simulated Data
Sample sizes: 50, 500, 2M
Signal-to-noise: High, low
Outcome Y: Binary, dichotomized
Yes/No High/Low

7. Study Design
Covariates:
X ~ U(-0.5,0.5)
e ~ N(0,s2)
Simulation Models:
y = 0.5 + β1x1 + ε
y = 0.5 + ε
y = 0.5 + β1x1 + β2x2 + ε
Signal-to-noise:
High: s=0.01, β1=1, (β2=0.01)
Low: s=0.10, β1=0.10, (β2=0.45)
Outcome Origin:
Binary: yb ~ Bernoulli (y)
Dichotomized: yd = I(y ≥ median(y))
Estimated Models:
y = 0.5 + β1x1 + ε
y = 0.5 + β1x1 + β2x2 + ε
Prediction:
n=500 holdout sample
Logit and Probit models

8. Binary Y
High Signal-to-noise Low Signal-to-noise
n=50
n=500
n=2M
— True Model
--- LPM y=0.5+b1x1+ε
--- LPM using WLS
Simulated: yb~Bernoulli(0.5+b1x1+e )
Fitted: Correctly-specified model
Goal: Estimate slope (b1)
Binary Y:
With large sample, LPM
is fine for estimation
𝐸 𝛽 𝑏 = 𝛽 +
𝑋′ 𝑋
𝑛
−1
𝑋′ 𝜀
𝑛
𝑛→∞
𝜷
Even with low signal

9. High Signal-to-noise Low Signal-to-noise
n=50
n=500
n=2M
Y=0 Y=0Y=1 Y=1
Binary Y:
LPM predictive power
same as logit/probit;
depends on signal (not n)
Binary Y
Goal: Predict 500 new records
Logit Probit LPM LPM using WLS

10. Dichotomized Y
High Signal-to-noise Low Signal-to-noise
n=50
n=500
n=2M
— OLS (numerical Y)
--- LPM (yd)
--- LPM using WLS
Dichotomized Y:
LPM gives biased coefs
𝛽 𝑑 =
1
2𝜋𝜎 𝑦
𝛽
WLS makes it worse
Can correct bias if sy can be estimated
Simulated: y=0.5+b1x1+e , yd=I(y>med)
Fitted: Correctly-specified model
Goal: Estimate slope (b1)

11. Dichotomized Y
High Signal-to-noise Low Signal-to-noise
n=50
n=500
n=2M
Logit
Probit
LPM
LPM+WLS
Y=0 Y=0Y=1 Y=1
Dichotomized Y:
LPM predictive power
similar to logit/probit;
depends on signal (not n)
LPM+WLS is best
Goal: Predict 500 new records

12. Dichotomized Y:
• LPM gives biased coefficients
WLS makes it worse
Can correct bias with estimate of sy
• Predictive power similar to logit/probit;
depends on signal (not n)
WLS improves predictive power
Quick Summary: Correctly specified model
Binary Y:
• With large n, LPM is fine for estimation
Even with low signal
• LPM predictive power same as
logit/probit; depends on signal (not n)

13. Over-specified models
b1 is of interest
Simulated: y = 0.5 + β1x1 + ε
Estimated: y = 0.5 + β1x1 + β2x2 + ε
Simulated: y = 0.5 + ε
Estimated: y = 0.5 + β1x1 + ε
Binary Y:
• b1 coef insignificant
All sample sizes
• Prediction=logit/probit
WLS doesn’t help
Binary Y:
• b1 (and b2) coefs unbiased
For n=2M, identical to OLS
• Prediction=logit/probit
WLS doesn’t help
Dichotomized Y:
• b1 coef insignificant
All sample sizes
• Prediction=logit/probit
WLS improves prediction
Dichotomized Y:
• b1 coef biased
Worse with WLS; can correct bias
• Prediction=logit/probit
WLS improves prediction

14. Modeling Auction Price
300,000 eBay auctions (Aug 2007- Jan 2008)
Price = f(min_bid, duration, seller_feedback, reserve)
1. Estimation/inference: determinants of price
2. Prediction: holdout sample (n = 5,000)
Dichotomized
Price

15. Inference/Estimation
Sample so large: all coefficients significant!
Bias due to dichotomization - corrected

16. Prediction
Removal of outliers gives identical ROC curves

17. Study Conclusions
• Explanatory modeling with a binary outcome –
large sample needed to reduce bias.
• Explanatory modeling with dichotomous outcome
requires sy to correct bias.
• Predicting a binary outcome (without WLS) or
dichotomous outcome (with WLS) – sample size
irrelevant
• Robust to over- or under-specified models
LPM is rare in IS