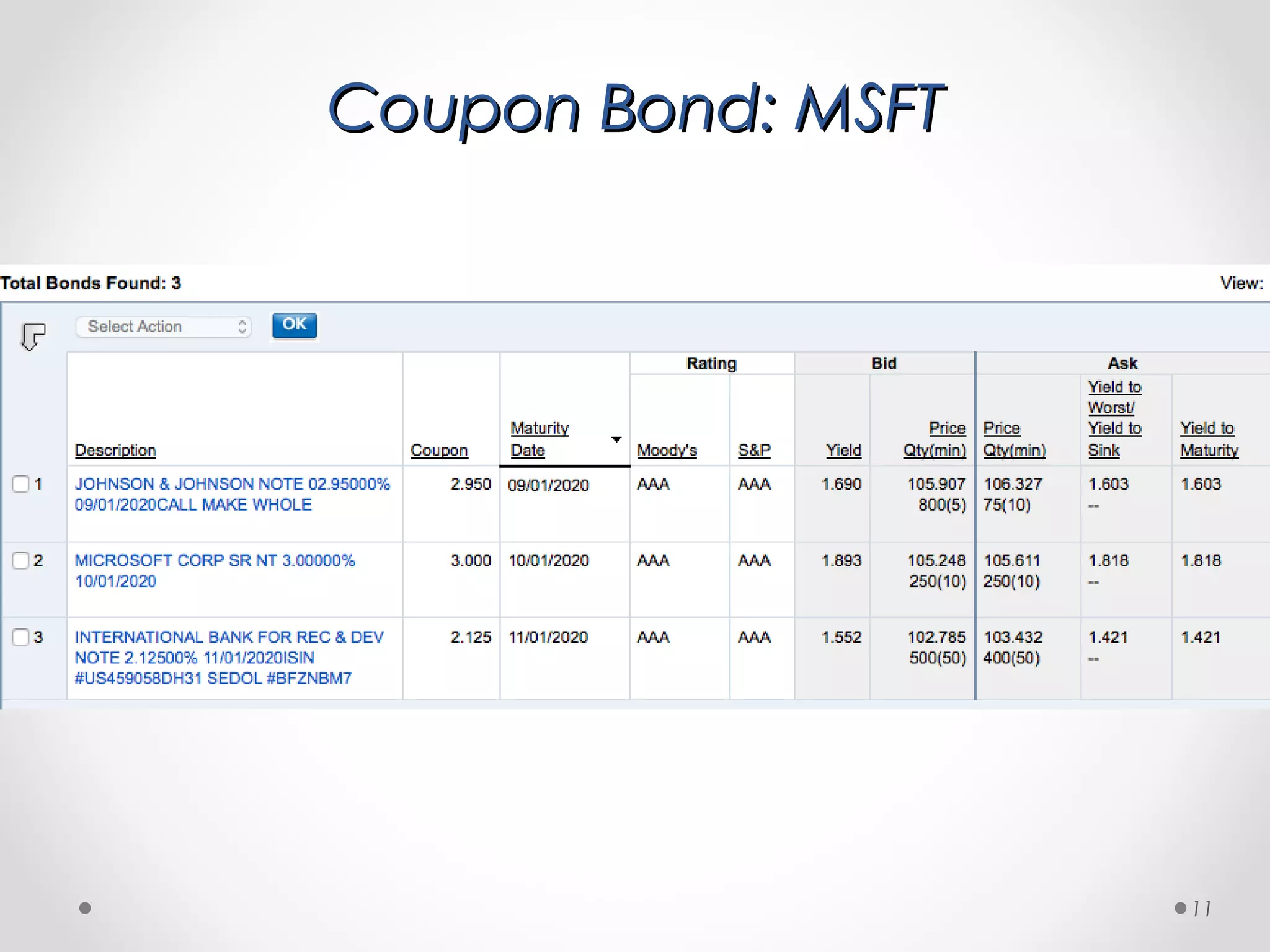
The document provides a comprehensive overview of bond pricing and yields, detailing key bond parameters such as principal, yield, maturity, and coupon rates. It explains calculations for bond prices and yields for both zero coupon and coupon bonds, alongside practical examples. Additionally, it addresses concepts like reinvestment risk and the impact of cash flow timing on bond pricing.

1. Bond Prices and YieldsBond Prices and Yields
Part 1Part 1

2. Learning ObjectivesLearning Objectives
• Types of bonds
• Bond parameters including yield
• Bond price as discounted expected cash flow
o Applications
• Compute bond yield from a known price
• Compute bond price from a known yield
• Plot bond price v. yield
• Compute bond price when yield is not known
• Plot bond price v. time to maturity
• Compute mortgage payments
• Bond formulas
• Bond price quotes
2

3. Bond OverviewBond Overview
• Corporations and governments can raise capital by selling
bonds
o Long term liability (accounting)
o Debt capital (finance)
• The bond has
o Principal, par, or face value: F
o Price: P
o Yield: y (also the discount rate )
o Maturity date, time to maturity, term, or tenor: T
• Date at which the bond principal, F, is returned to investors
• This is different than the duration
o In the case of a coupon bond (not a zero coupon bond)
• Coupon rate: c (annual, simple, nominal rate)
• Annual payment frequency: m; or period ∆t
o In the U.S. semiannual coupons is typical: m = 2 or ∆t = .5
3

4. Zero Coupon BondsZero Coupon Bonds
• ZCBs do not pay a coupon
o No intermediate cash flow
• The rate of return or ‘yield’ is due to the bond being bought,
at P, a discount to face value, F
• U.S. Treasury bills (T – bills) are zero coupon bonds
o Time-to-maturity at issue is 4, 13, 26, 52 weeks
o Face value $100 to $5,000,000
• A ZCB yield is the interest rate,
(and the discount rate) denoted z
4
F
P
t=0
t=T

5. Zero Coupon BondZero Coupon Bond
• For T ≤ 1 year:
where z is the annual yield – a simple rate
• For T > 1 year
where z is the annualized yield – an effective rate
If a bond has a term of a year or less, simple interest is used,
otherwise compound annual interest is used
5
P=
F
(1+z×T)
P=
F
(1+z)T
F
P
t=0
t=T

6. Zero Coupon Bond ExampleZero Coupon Bond Example
• The face value is $1000, the market price is $850, and the time
to maturity is 3.5 years. What is the annualized yield ?
• The face value is $1000, the market price is $975, and the
time-to-maturity is 0.5 years. What is the annualized yield?
6
$850=
$1000
(1+y)3.5
y=
$1000
$850





÷
1
3.5
-1=4.753%
P=
F
(1+z×T)
$975=
$1000
(1+0.5×y)
y=2×
$1000
$975
-1





÷=5.128%
P =
F
(1+z)T

7. Zero Coupon BondZero Coupon Bond
• A bond dealer can split a coupon bond into ZCBs
o one for the principal and
o one for each coupon
o This is called ‘stripping’ the bond
• The advantage of a ZCB is that there is no reinvestment risk
• For a ZCB, the yield, y, is the zero coupon rate denoted as z
7

8. Coupon BondCoupon Bond
8

9. Coupon Bond: MSFTCoupon Bond: MSFT
9
June 30

10. Coupon Bond: MSFTCoupon Bond: MSFT
10
June 30

11. Coupon Bond: MSFTCoupon Bond: MSFT
11

12. Coupon BondCoupon Bond
12
P =
current
price
C = coupon payment
c = coupon rate (simple interest)
F = face
or par
value
t=0.0 t=∆t t=2∙∆t t=m∙N∙∆t=T
i=0 i=1 i=2 i=m∙N
t0=0.0 t1=∆t t2=2∆t tm∙N= m∙N∙∆t =T
12

13. Coupon PaymentCoupon Payment
• Bond coupon cash flows, C, are defined by a nominal, simple
coupon rate, c, and a compounding frequency per year, m,
or coupon period measured in years, ∆t
o m is always 1 or 2 for a bond
o ∆t = .5 or 1 year
• The total cash flow at time ti, CFi, is defined as:
13
CFi = C for i < m×N
CFm×N = C + F
C = c×F×∆t =
c×F
m
example
c=1.625%
F=$1000
∆t=.5
C = $8.125
Effective coupon rate
c= 1+
c
m





÷
m
-1
c= 1+
1.625%
2





÷
2
-1=1.632%

14. Current interest and yield summaryCurrent interest and yield summary
• Bloomberg
• Yahoo
• Bankrate
14

15. Coupon Bond YieldCoupon Bond Yield
• Yield to maturity is the actual yield achieved for a coupon bond if
o The bond is held to maturity, and
o Each coupon payment is reinvested at the rate of return y through time T
• The risk that coupons cannot be reinvested at a rate greater than or equal to y
due to market conditions is called “reinvestment risk”
• The yield to maturity, y, is the investor’s expected return on the
investment of P and is thus the issuer’s rate cost
o It’s the issuer’s ‘cost of debt’, kD, for the bond
• The yield reflects both the time value of money and the credit risk of
the borrower
o The expected variance of the cash flows is reflected in the yield, y
15

16. Bond PriceBond Price
• The discount rate y is the yield to maturity or simply the yield
on a coupon bond
• It’s the internal rate of return that sets the discounted cash
flow on the right hand side to the market price of the bond, P,
on the left hand sidex4
16
P=
CFi
(1+y)ti
i=1
M
∑P=
CFi
1+
y
m





÷
i
i=1
M
∑
y is the nominal annual
yield to maturity
y is effective annual
yield to maturity
M is the number of periods or “cash flows”
M = N * m if N is an integer number of years
M = T * m if T is floating point years

17. Homework 10Homework 10
• Compute the price, P, of the following bond and
the nominal yield to maturity, y
o Time to maturity 4.5 years
o Annual, nominal coupon rate is 7%
o Semi annual coupons and compounding
o Par value is $1000
o Yield to maturity 8% (effective annual rate)
• Submit a knitr pdf with explanation and echoed
code
o Print the data frame or table for clarity
17

18. Homework 11Homework 11
• Compute the nominal and effective yields to
maturity for this bond
o Time to maturity 4.5 years
o Annual, nominal coupon rate is 7%
o Semi annual coupons and compounding
o Par value is $1000
o Price is $900.00
• Submit a knitr pdf with explanation and echoed
code
o Print the data frame or table for clarity
18

19. • For a fractional initial coupon period: t1 < ∆t
Fractional Initial Time PeriodFractional Initial Time Period
For a bond with semi-annual coupons, assume that the next
coupon payment is in 3 months. The coupon payments occur at
t0=0.0, t1=0.25, t2=0.75, t3=1.25, t4 = 1.75, …
i=0 i=1 i=2 i=M
t0=0.0 t1 t2=t1+∆t tM= T
C = coupon payment
F = face
or par
value
19

20. Homework 12Homework 12
• Compute the price of this bond
o Time to maturity 4.25 years
o The next coupon is paid 3 months from present
o Annual, nominal coupon rate is 7%
o Semi annual coupons and compounding
o Par value is $1000
o Yield to maturity 8% (effective annual rate)
• Submit a knitr pdf with explanation and echoed
code
o Print the data frame or table for clarity
20

21. Bond Price to MaturityBond Price to Maturity
$825
$850
$875
$900
$925
$950
$975
$1,000
$1,025
$1,050
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5
Time
Price
21
• For a bond with price $840.34 at time 0, here’s a plot of price as
time progresses from 0 to 4.5 years assuming a constant yield to
maturity of 12%
• The plot is computed using the DCF formula. These prices are
referred to as ‘dirty’ prices. There are also ‘clean’ prices.

22. Homework 13Homework 13
• Plot price v. time for the following bond
o Time to maturity 10 years
o Annual, nominal, simple coupon rate is 5%
o Par value is $1000
o Effective annual yield to maturity is a constant 6%
o (It’s a saw tooth curve)
• Submit a knitr pdf with explanation and echoed
code
o Print the data frame or table for clarity
22