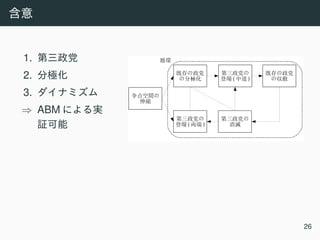
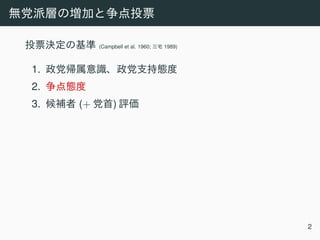
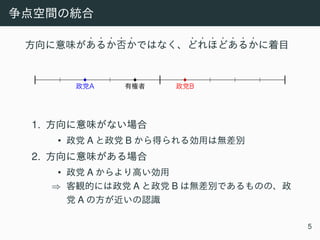
This document contains a literature review and outlines three statistical models to analyze political attitudes and behavior: 1. A Bayesian model is used to analyze left-right ideological positions and proximity to political parties. 2. A second model examines sophistication, engagement, and detachment in political thinking using individual-level data. 3. A third multi-level model analyzes country-level data on political knowledge to study how system-level factors like press freedom and competitiveness influence individuals. The document concludes by discussing future research directions.

1. – –
2018/03/07
0

2. Table of Contents
1

5. (Campbell et al. 1960; 1989)
1.
2.
3. (+ )
2

6. 1. (Downs 1957)
• Westholm (1997, 2001) Claassen (2007) Tomz and
Van Houweling (2008) Lacy and Paolino (2010)
2. (Rabinowitz and Macdonald 1989)
• Macdonald, Listhaug, and Rabinowitz (1991)
Macdonald, Rabinowitz, and Listhaug (1998)
3. !
• Lewis and King (1999) Merrill and Grofman (1999)
Weber (2015)
3

8. 2
•
•
•
• : ˙ ˙ ˙ ˙
×
• :
˙ ˙ ˙ (neutral point)
•
4

18. :
•
•
•
• ( )
• (projection)
⇒ (Lewis and King 1999)
9

21. A B
1
⃝ A ⃝ B
10

22. 10 ( )
1 9 6
2 7
3 8
4 9
5 10
10

23. Ci,A i A
(Ci,A ∈ {0,1})
Di i
(Di ∈ {−1,0,1})
Ii i
(Di ∈ {0,1,2,...,7})
ω
(0 ≤ ω ≤ 1)
Ci,A ∼ Bernoulli(θA
i ),
logit(θA
i ) = β0 +β1(Ui,A −Ui,B),
Ui,c = −|P
adj.
i −P
adj.
i,c |,
P
adj.
i = Di
Ii−1
∑
j=0
ωj
,
ω ∼ Normal+
(0,102
),
β ∼ Normal(0,102
) (1)
11

24. (ω)
( ( 5 ))
90% HPDI 90% HPDI
MAP MAP
1 0.897 0.864 0.925 6 0.921 0.891 0.951
2 1.017 0.986 1.052 7 0.940 0.908 0.970
3 0.937 0.900 0.966 8 0.918 0.889 0.951
4 0.920 0.886 0.952 9 0.909 0.873 0.940
5 0.935 0.901 0.969 10 0.957 0.924 0.989
2 Pr(ω < 1) > 0.9
12

25. 1. (Downs 1957)
2. (Rabinowitz and Macdonald 1989)
3. Representatinal Policy Leadership (Iversen 1994)
4. (Grofman 1985)
5.
• κ (Cohen 1960) WAIC (Watanabe 2010)
13

30. vs.
• Merrill (1995) Maddens (1996)
•
↑
• Merrill (1995)
• ( )
⇔ ( )
• (2005)
•
15

31. •
• (Deli Carpini and Keeter 1997)
• :
• & : ( 1985)
•
• :
• :
• :
•
16

32. : Luskin (1987)
DK
(IRT )
• (1985) (2006)
•
+
17

33. :
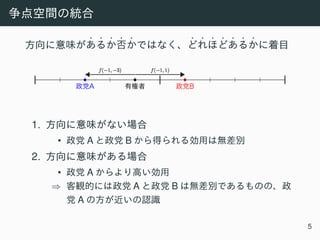
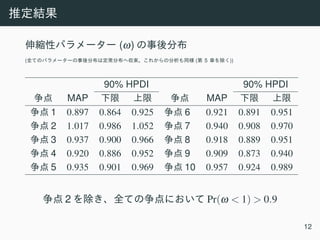
ω
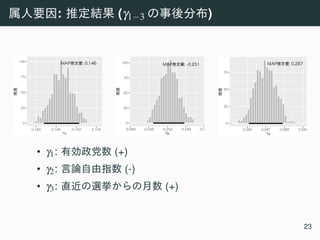
• ωi,j: j i
(j = {1,2,3,4};i = {1,2,...,N};ω ∈ [0,1])
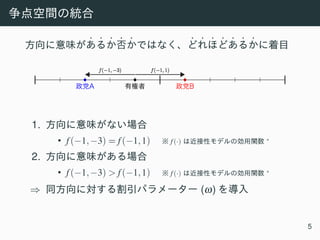
logit(ωi,j) = γ0,j +γ1Sophistication+γ2Engagement
γ3Detached+γ4Engagement·Detached,
γ0 ∼ Normal(2.669,0.490),
γ1∼4 ∼ Normal(0,104
). (2)
18

36. (CSES) 33
• ≃ ⇐
• ⇒
• ≃ ⇐
• & ⇒
• ≃ ⇐
• ⇒
21

37. :
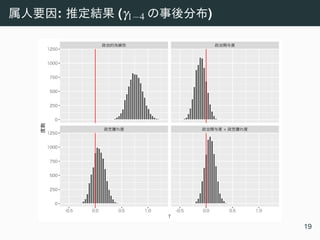
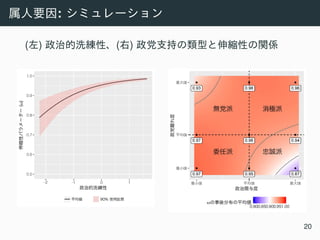
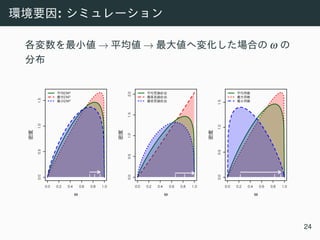
• ωi: i
• j[i]: i j
ωi ∼ Beta(θj[i]φj[i],(1−θj[i])φj[i]),
logit(θj[i]) = γ0 +logENPj[i] +logPressj[i] +logLastj[i],
φ ∼ Normal+
(0,104
),
γ ∼ Normal(ζγ
,τγ
),
ζ ∼ Cauchy(0,104
),
τ ∼ Cauchy+
(0,104
). (3)
22

38. :
( 1)
1.
•
2. ( ) : →
• j i
• (random-effect)
•
(three-level)
• (2 ∼ 9 ) ← ←
22

42. •
⇔
•
•
• ↑
• ( )
•
• :
• :
25

45. 1.
2.
3.
⇒ ABM
争点空間の
伸縮
既存の政党
の分極化
第三政党の
登場 両端
第三政党の
登場 中道
既存の政党
の収斂
第三政党の
消滅
循環
26

46. •
•
•
• ?
•
• :
• :
•
•
• JES
27