1) The document derives the formula for the volume of a square-based pyramid using integration. 2) It models the pyramid with the base at the origin and height along the x-axis, and considers the volume as the sum of cross-sectional areas from the base to the vertex. 3) Through similar triangles and integrating the changing cross-sectional areas, it arrives at the formula Volume = (1/3) x Area of Base x Height.

1. Using Integration to develop the formula for the volume of a square based pyramid.
Volume of a pyramid is 𝑉 =
1
3
𝐴𝐻 𝑤ℎ𝑒𝑟𝑒 𝐴 𝑖𝑠 𝑡ℎ𝑒 𝑎𝑟𝑒𝑎 𝑜𝑓 𝑡ℎ𝑒 𝑏𝑎𝑠𝑒 𝑎𝑛𝑑 𝐻 𝑖𝑠 𝑡ℎ𝑒 ℎ𝑒𝑖𝑔ℎ𝑡
 Position the pyramid withits base at the origin and its height along the x-axis. ABCD isa planeat the origin positioned
into the page. 𝐸(0, 𝐻) is the vertex of the pyramid.
 The volumeof the pyramid willbe the sum of the cross-sectional areas from the base of the pyramid (theorigin) to its
vertex 𝐸(0, 𝐻).
 The area of each the cross-section of the pyramid (in this case a square) is dependenton thedistance that the square is
along the x-axis.
 𝐹𝑜𝑟 𝑐𝑜𝑛𝑣𝑒𝑛𝑖𝑒𝑛𝑐𝑒 𝑎𝑙𝑙𝑜𝑤 𝑡ℎ𝑒 𝑏𝑎𝑠𝑒 𝑡𝑜 ℎ𝑎𝑣𝑒 𝑎 𝑠𝑖𝑑𝑒 𝑙𝑒𝑛𝑔𝑡ℎ 𝑜𝑓 2𝑎 𝑎𝑛𝑑 𝑎 ℎ𝑒𝑖𝑔ℎ𝑡 𝑜𝑓 𝐻,
𝐴𝑡 𝑥 = 0 𝑡ℎ𝑒 𝑎𝑟𝑒𝑎 𝑜𝑓 𝑡ℎ𝑒 𝑐𝑟𝑜𝑠𝑠 𝑠𝑒𝑐𝑡𝑖𝑜𝑛𝑎𝑙 𝑎𝑟𝑒𝑎 ( 𝑡ℎ𝑒 𝑏𝑎𝑠𝑒) 𝑖𝑠 𝐴 = 2𝑎 × 2𝑎
𝑎𝑡 𝑥 = 𝐻 𝑡ℎ𝑒 𝑎𝑟𝑒𝑎 𝑤𝑖𝑙𝑙 𝑏𝑒 0

2.  𝐶𝑜𝑛𝑠𝑖𝑑𝑒𝑟 𝑎 𝑔𝑒𝑛𝑒𝑟𝑎𝑙 𝑝𝑜𝑖𝑛𝑡 𝐹( 𝑥, 0) 𝑤ℎ𝑒𝑟𝑒 0 ≪ 𝑥 ≤ 𝐻
𝐿𝑒𝑡 𝑡ℎ𝑒 𝑐𝑟𝑜𝑠𝑠 𝑠𝑒𝑐𝑡𝑖𝑜𝑛𝑎𝑙 𝑎𝑟𝑒𝑎 𝑎𝑡 𝑡ℎ𝑖𝑠 𝑝𝑜𝑖𝑛𝑡 𝑏𝑒 2𝑘 × 2𝑘
𝑇ℎ𝑖𝑠 𝑎𝑟𝑒𝑎 𝑐ℎ𝑎𝑛𝑔𝑒𝑠 𝑤𝑖𝑡ℎ 𝑥. 𝑊𝑒 𝑛𝑒𝑒𝑑 𝑡𝑜 𝑓𝑖𝑛𝑑 𝑡ℎ𝑖𝑠 𝑎𝑟𝑒𝑎 𝑎𝑠 𝑎 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛 𝑜𝑓 𝑥.
 𝐹𝑖𝑟𝑠𝑡 𝑓𝑖𝑛𝑑 𝑘 𝑎𝑠 𝑎 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛 𝑜𝑓 𝑥
𝐶𝑜𝑛𝑠𝑖𝑑𝑒𝑟∆𝐸𝑂𝑇
𝐵𝑦 𝑠𝑖𝑚𝑖𝑙𝑎𝑟 𝑡𝑟𝑖𝑎𝑛𝑔𝑙𝑒𝑠
𝑘
𝑎
=
𝐻 − 𝑥
ℎ
𝐻𝑘 = 𝑎( 𝐻 − 𝑥)
𝐻𝑘 = 𝑎𝐻 − 𝑎𝑥
𝑘 =
𝑎( 𝐻 − 𝑥)
𝐻

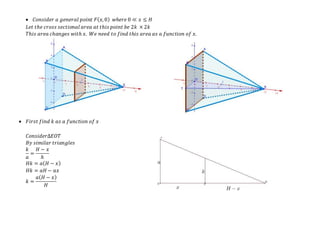
3.  𝐹𝑖𝑛𝑑 𝑡ℎ𝑒 𝑎𝑟𝑒𝑎 𝑜𝑓 𝑡ℎ𝑒 𝑐𝑟𝑜𝑠𝑠 𝑠𝑒𝑐𝑡𝑖𝑜𝑛 𝑜𝑓 𝑡ℎ𝑒 𝑝𝑦𝑟𝑎𝑚𝑖𝑑 𝑖𝑛 𝑡𝑒𝑟𝑚𝑠 𝑜𝑓 𝑥
𝐴𝑟𝑒𝑎 = 2𝑘 × 2𝑘
= 4𝑘2
= 4 [
𝑎( 𝐻 − 𝑥)
𝐻
]
2
=
4𝑎2( 𝐻 − 𝑥)2
𝐻2
=
4𝑎2
𝐻2
(𝐻2
− 2𝐻𝑥 + 𝑥2
)
 𝐹𝑖𝑛𝑑 𝑡ℎ𝑒 𝑣𝑜𝑙𝑢𝑚𝑒 𝑜𝑓 𝑡ℎ𝑒 𝑝𝑦𝑟𝑎𝑚𝑖𝑑 𝑏𝑦 𝑠𝑢𝑚𝑚𝑖𝑛𝑔 𝑡ℎ𝑒 𝑎𝑟𝑒𝑎𝑠 𝑜𝑓 𝑡ℎ𝑒 𝑐𝑟𝑜𝑠𝑠 𝑠𝑒𝑐𝑡𝑖𝑜𝑛 𝑓𝑟𝑜𝑚 𝑥 = 0 𝑡𝑜 𝑥 = 𝐻
= ∫
4𝑎2
𝐻2
( 𝐻2
− 2𝐻𝑥 + 𝑥2) 𝑑𝑥
𝐻
0
=
4𝑎2
𝐻2
∫ 𝐻2
− 2𝐻𝑥 + 𝑥2
𝑑𝑥
𝐻
0
=
4𝑎2
𝐻2
[ 𝐻2
𝑘 − 𝐻𝑘2
+
𝑥3
3
]
=
4𝑎2
𝐻2
[(𝐻3
− 𝐻3
+
𝐻3
3
) − (0)]
=
4𝑎2
𝐻2
×
𝐻3
3
=
4𝑎2
𝐻
3
𝑔𝑖𝑣𝑒𝑛 𝑡ℎ𝑒 𝑎𝑟𝑒𝑎 𝑜𝑓 𝑡ℎ𝑒 𝑏𝑎𝑠𝑒 𝐴 = 2𝑎 × 2𝑎 = 4𝑎2
𝑉𝑜𝑙𝑢𝑚𝑒 𝑜𝑓 𝑝𝑦𝑟𝑎𝑚𝑖𝑑 =
1
3
𝐴𝐻 𝑎𝑠 𝑟𝑒𝑞𝑢𝑖𝑟𝑒𝑑