Recommended
PDF
PDF
PPT
наша первая экскурсия в осенний лес
PDF
PPTX
PDF
【AWS Summit2013】チームラボ流クラウドスピードクッキング~この講演中にゼロからサービス一個立ちあげます~
PDF
PDF
PPTX
PDF
Unity × graphics × effects
PPTX
Robot upgrade school to SICTIC2013
PPTX
PPTX
チームラボ スマホアプリチームの面白い仕事の作り方
PPTX
Pepperモーション制作ハッカソン 〜チームラボ流モーション制作術〜 【前編】
PPTX
PDF
チームラボ流 デジタルマーケティングにおけるクラウド活用術
PDF
PDF
WebRTC開発者向けプラットフォーム SkyWayの裏側
PDF
20140321 makershub 専門家が手を動かしながら、
PPTX
20160706 深圳最新情報 メイカーズのエコシステム 東大暦本研,筑波大落合研
PPTX
ここまで来た!2017年 Web VRでできること
PPTX
WebRTC NextVersion時代のJavaScript開発
PPTX
メイカームーブメントで世界の何が変わってるのか? 2015/07/29 明治大学講演
PDF
Cotocoto ac43 slide20140922_v2
PPTX
More Related Content
PDF
PDF
PPT
наша первая экскурсия в осенний лес
PDF
PPTX
PDF
【AWS Summit2013】チームラボ流クラウドスピードクッキング~この講演中にゼロからサービス一個立ちあげます~
PDF
PDF
Viewers also liked
PPTX
PDF
Unity × graphics × effects
PPTX
Robot upgrade school to SICTIC2013
PPTX
PPTX
チームラボ スマホアプリチームの面白い仕事の作り方
PPTX
Pepperモーション制作ハッカソン 〜チームラボ流モーション制作術〜 【前編】
PPTX
PDF
チームラボ流 デジタルマーケティングにおけるクラウド活用術
PDF
PDF
WebRTC開発者向けプラットフォーム SkyWayの裏側
PDF
20140321 makershub 専門家が手を動かしながら、
PPTX
20160706 深圳最新情報 メイカーズのエコシステム 東大暦本研,筑波大落合研
PPTX
ここまで来た!2017年 Web VRでできること
PPTX
WebRTC NextVersion時代のJavaScript開発
PPTX
メイカームーブメントで世界の何が変わってるのか? 2015/07/29 明治大学講演
PDF
Cotocoto ac43 slide20140922_v2
PPTX
あるTweetから調べたmin suffixの話 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. w’=UV | ... | UV | U を満たすU,Vを探すには、
ある位置xで、xからはじまるsuffixがw’のprefixになってい
ればよい(xは最初の|の直後の位置になる)。
これはZ algorithmをw’にかけておくと各xについてO(1)で
調べることができる。
14
15. 16. 各Lyndon Word Lについて、Z algorithmを適用し、
任意のy≦|L|について、
1≦x≦yかつz[x]+x≧y を満たす最小のxを見つければ良い。
x=yのときはL[0,y)はfactorizeされないのでL[0]の位置が答
え。
x<yのときはU=L[0,y%x)になる。すこし横着して(L[0,y-x)
のときの答え)+xになる。
16
17. 18. 19. 20. 参考文献
・Duval, Jean-Pierre (1983), "Factorizing words over an ordered alphabet", Journal of Algorithms 4 (4)
・Apostolico, A., and Crochemore, M., Optimal canonization of all substrings of a string, Information
and Computation 95, 1 (1991): 76--95.
・Maxim A. Babenko, Pawel Gawrychowski, Tomasz Kociumaka, Tatiana A. Starikovskaya:
Computing Minimal and Maximal Suffixes of a Substring Revisited. CPM 2014: 30--39
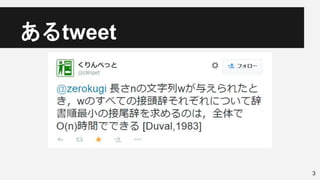
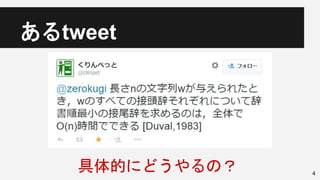
・https://twitter.com/climpet/status/598440489935769601
20
Editor's Notes #3 戦績を書こうと思ったが大きな大会で特に入賞していないので書きませんでした #4 あとで説明するので割りと早めに #19 時間がなければ飛ばして良い

![例
5
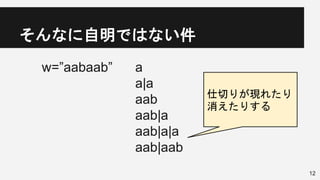
w = “aabaab”
w[0,0]=”a”の辞書順最小の接尾辞(min suffix)は”a”
w[0,1]=”aa” -> “a”
w[0,2]=”aab” -> “aab”
w[0,3]=”aaba” -> “a”
w[0,4]=”aabaa” -> “a”
w[0,5]=”aabaab” -> “aab”
上記を求める。](https://image.slidesharecdn.com/tweetminsuffix1-150525141501-lva1-app6891/85/Tweet-min-suffix-5-320.jpg)

![Suffix Array?
7
3
0
4
1
5
2
aab
aabaab
ab
abaab
b
baab
[0,4]からはじまる
wの最小のsuffixは3(aab)だが、
w[0,4]の最小のsuffixは4(a[b])
Suffix Arrayでの最小値をそのま
ま答えに出来るわけではない。](https://image.slidesharecdn.com/tweetminsuffix1-150525141501-lva1-app6891/85/Tweet-min-suffix-7-320.jpg)
![Suffix Array?
8
3
0
4
1
5
2
aab
aabaab
ab
abaab
b
baab
[0,4]からはじまる
wの最小のsuffixは3(aab)だが、
w[0,4]の最小のsuffixは4(a[b])
Suffix Arrayでの最小値をそのま
ま答えに出来るわけではない。
未知のアルゴリズムの予感!!](https://image.slidesharecdn.com/tweetminsuffix1-150525141501-lva1-app6891/85/Tweet-min-suffix-8-320.jpg)





![Z algorithm
各iについて、wのi文字目以降とwとの共通prefixの長さを格
納した配列をO(n)でつくるアルゴリズム。
w=”aabaab”
z_w=[6,1,0,3,1,0]
i=4では”ab”と”aabaab”の共通prefixは”a”なのでz_w[4]=1.
15](https://image.slidesharecdn.com/tweetminsuffix1-150525141501-lva1-app6891/85/Tweet-min-suffix-15-320.jpg)
![各Lyndon Word Lについて、Z algorithmを適用し、
任意のy≦|L|について、
1≦x≦yかつz[x]+x≧y を満たす最小のxを見つければ良い。
x=yのときはL[0,y)はfactorizeされないのでL[0]の位置が答
え。
x<yのときはU=L[0,y%x)になる。すこし横着して(L[0,y-x)
のときの答え)+xになる。
16](https://image.slidesharecdn.com/tweetminsuffix1-150525141501-lva1-app6891/85/Tweet-min-suffix-16-320.jpg)
![例のO(n)のアルゴリズム
wのLyndon Factorizationを求める。
各Lyndon Word Lについて
Z algorithmでz[]を求める。
reach:=0,argmax:=-1
y=1→|L|-1
reach>=yなら求めるxはargmaxで、そうでなければyである。x=yのと
きはL[0]の位置が答え。x<yのときは(L[0,y-x)のときの答え)+xになる。
z[y]+y > reachならreach:=z[y]+y, argmax:=yとする。
y=0のはL[0]の位置が答え。
17](https://image.slidesharecdn.com/tweetminsuffix1-150525141501-lva1-app6891/85/Tweet-min-suffix-17-320.jpg)
![例
w=”aabaab”
LyndonFactorization(w)=aab|aab
z_“aab”=[3,1,0]
minsuffixlen=[1,1,3,1,1,3]
18](https://image.slidesharecdn.com/tweetminsuffix1-150525141501-lva1-app6891/85/Tweet-min-suffix-18-320.jpg)

