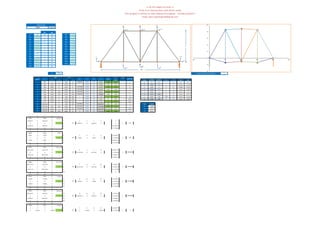
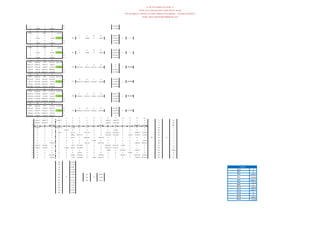
This document contains information about optimizing a Pratt truss structure using Excel Solver, including: - The program was written by Salar Delavar Ghashghaei on February 12, 2017. - It provides member cross-sectional areas, displacement results from the optimization, and equilibrium equations for the joints of the truss structure. - The objective is to minimize the total weight of the truss subject to stress constraints on each member.

1. >> IN THE NAME OF GOD <<
Truss Optimization with EXCEL Solver
This program is written by Salar Delavar Ghashghaei ‐ 12/February/2017
Email: salar d ghashghaei@gmail comEmail: salar.d.ghashghaei@gmail.com
weight
Target Function
14.67207125
5.732818824
6.34433E‐07
W=0.5[P]{Δ}
[K]{Δ}‐[P]=0
Min Max
A1= 6.62375 5 30
A2= 5 5 30
A3= 7.26792 5 30
A4= 5 5 30
A5= 5 5 30
A6= 5 5 30
A7= 5.36694 5 30
5 3 1
3
4 8
7 11
12
1 2
A8= 5 5 30
A9= 5 5 30
A10= 5 5 30
Δ5= ‐0.6269
Δ6= ‐1.8807
Δ7= 0.62689
Δ8= ‐1.7443
Δ9= ‐0.8855
Δ10= ‐3.9882
h5 6
7
8
9
10
Δ11= 0.8037
Δ12= ‐3.8113
L= 9.144
h= 9.144
0.600
6 4 2
2
1 5
6
9
10
L L
3 4
E P
member L
start end
A Fy stress ratioP/A
F.S 1.667 node coordinate-X coordinate-Y Px Py Ux Uy
x y x y 0.6Fy 1 18.288 9.144 0 0 0.804 ‐3.811
1 9.144 0 3 9.144 3 6.624 2100000 2400 9536.294 1439.712 1439.712 1 2 18.288 0 0 -5 ‐0.886 ‐3.988
2 9.144 9.144 9.144 18.288 9.144 5.000 2100000 2400 2030.251 406.050 1439.712 0.28 3 9.144 9.144 0 0 0.627 ‐1.744
3 9.144 0 0 9.144 0 7.268 2100000 2400 ‐10463.7 1439.712 1439.712 1 4 9.144 0 0 ‐5 ‐0.627 ‐1.881
4 9.144 9.144 0 18.288 0 5.000 2100000 2400 ‐2969.75 593.950 1439.712 0.41
5 9.144 9.144 0 9.144 9.144 5.000 2100000 2400 1566.545 313.309 1439.712 0.22
6 9.144 18.288 0 18.288 9.144 5.000 2100000 2400 2030.251 406.050 1439.712 0.28
7 12.9316 9.144 0 0 9.144 5.367 2100000 2400 7726.848 1439.712 1439.712 1
E P
member L
start end
A Fy stress ratioP/A
8 12.9316 0 0 9.144 9.144 5.000 2100000 2400 ‐6415.29 1283.058 1439.712 0.89
9 12.9316 18.288 0 9.144 9.144 5.000 2100000 2400 4199.859 839.972 1439.712 0.58
10 12.9316 9.144 0 18.288 9.144 5.000 2100000 2400 ‐2871.21 574.242 1439.712 0.4
3 4 7 8
lanada-x 1 landa-y 0 15212
15212.03 0 ‐15212 0 3 3 4 7 8 0
0 0 0 0 1 4 q1= ‐15212 0 15212.02552 0 0 = 9536.294
‐15212 0 15212 0 7 0.627
0 0 0 0 8 ‐1.744
7 8 11 12
lanada-x 1 landa-y 0 11482.9
11482.94 0 ‐11483 0 7 7 8 11 12 0.627
0 0 0 0 2 8 q2= ‐11482.9 0 11482.93963 0 ‐1.744 = 2030.251
‐11482.9 0 11482.9 0 11 0.804
0 0 0 0 12 ‐3.811
1 2 5 6
lanada-x 1 landa-y 0 16691.4
16691.41 0 ‐16691 0 1 1 2 5 6 0
0 0 0 0 3 2 q3= ‐16691.4 0 16691.40843 0 0 = -10463.71
‐16691.4 0 16691.4 0 5 ‐0.627
0 0 0 0 6 ‐1.881
5 6 9 10
lanada-x 1 landa-y 0 11482.9
11482.94 0 ‐11483 0 5 5 6 9 10 ‐0.627
0 0 0 0 4 6 q4= ‐11482.9 0 11482.93963 0 ‐1.881 = -2969.749
‐11482.9 0 11482.9 0 9 ‐0.88551444
0 0 0 0 10 ‐3.988
5 6 7 8
lanada-x 0 landa-y 1 11482.9
0 0 0 0 5 5 6 7 8 ‐0.627
0 11482.94 0 ‐11482.9 5 6 q5= 0 ‐11482.93963 0 11482.94 ‐1.881 = 1566.545
0 0 0 0 7 0.627
0 ‐11482.9 0 11482.94 8 ‐1.744
9 10 11 12
lanada-x 0 landa-y 1 11482.9
0 0 0 0 9 9 10 11 12 ‐0.88551444
0 11482.94 0 ‐11482.9 6 10 q6= 0 ‐11482.93963 0 11482.94 ‐3.988 = 2030.251
0 0 0 0 11 0.804
0 ‐11482.9 0 11482.94 12 ‐3.811
5 6 3 4
lanada-x ‐0.70711 landa-y 0.707107 8715.55
4357.775 ‐4357.77 ‐4357.8 4357.775 5 5 6 3 4 ‐0.627
‐4357.77 4357.775 4357.77 ‐4357.77 7 6 q7= 6162.824 ‐6162.824467 ‐6162.824467 6162.824 ‐1.881 = 7726.848
‐4357.77 4357.775 4357.77 ‐4357.77 3 0
4357.775 ‐4357.77 ‐4357.8 4357.775 4 0
1 2 7 8
lanada-x 0.707107 landa-y 0.707107 8119.66
4059.832 4059.832 ‐4059.8 ‐4059.83 1 1 2 7 8 0
4059.832 4059.832 ‐4059.8 ‐4059.83 8 2 q8= ‐5741.47 ‐5741.469816 5741.469816 5741.47 0 = -6415.288
‐4059.83 ‐4059.83 4059.83 4059.832 7 0.627
‐4059.83 ‐4059.83 4059.83 4059.832 8 ‐1.744
9 10 7 8
lanada-x ‐0.70711 landa-y 0.707107 8119.66
4059 832 4059 83 4059 8 4059 832 9 9 10 7 8 0 885514444059.832 ‐4059.83 ‐4059.8 4059.832 9 9 10 7 8 ‐0.88551444
‐4059.83 4059.832 4059.83 ‐4059.83 9 10 q9= 5741.47 ‐5741.469816 ‐5741.469816 5741.47 ‐3.988 = 4199.859
‐4059.83 4059.832 4059.83 ‐4059.83 7 0.627
4059.832 ‐4059.83 ‐4059.8 4059.832 8 ‐1.744
5 6 11 12
lanada-x 0.707107 landa-y 0.707107 8119.66
4059.832 4059.832 ‐4059.8 ‐4059.83 5 5 6 11 12 ‐0.627
4059.832 4059.832 ‐4059.8 ‐4059.83 10 6 q10= ‐5741.47 ‐5741.469816 5741.469816 5741.47 ‐1.881 = -2871.209
‐4059.83 ‐4059.83 4059.83 4059.832 11 0.804
4059 83 4059 83 4059 83 4059 832 12 3 811‐4059.83 ‐4059.83 4059.83 4059.832 12 ‐3.811
1 2 3 4 5 6 7 8 9 10 11 12
1 20751.2 4059.83 0 0 ‐16691.40843 0 ‐4059.83 ‐4059.83 0 0 0 0 0 Q1
2 4059.83 4059.83 0 0 0 0 ‐4059.83 ‐4059.83 0 0 0 0 0 Q2
3 0 0 19569.8 ‐4357.77 ‐4357.774972 4357.774972 ‐15212 0 0 0 0 0 0 Q3
4 0 0 ‐4357.77 4357.775 4357.774972 ‐4357.774972 0 0 0 0 0 0 0 Q4
5 16691 4 0 4357 77 4357 775 36591 95527 297 9427306 0 0 11482 9396 0 4059 83 4059 83 D5 05 ‐16691.4 0 ‐4357.77 4357.775 36591.95527 ‐297.9427306 0 0 ‐11482.9396 0 ‐4059.83 ‐4059.83 D5 0
6 0 0 4357.775 ‐4357.77 ‐297.9427306 19900.54685 0 ‐11482.9 0 0 ‐4059.83 ‐4059.83 D6 ‐5000
7 ‐4059.83 ‐4059.83 ‐15212 0 0 0 34814.63 0 ‐4059.83224 4059.832 ‐11482.9 0 D7 0
8 ‐4059.83 ‐4059.83 0 0 0 ‐11482.93963 0 19602.6 4059.83224 ‐4059.832 0 0 D8 0
9 0 0 0 0 ‐11482.93963 0 ‐4059.83 4059.832 15542.7719 ‐4059.832 0 0 D9 0
10 0 0 0 0 0 0 4059.832 ‐4059.83 ‐4059.83224 15542.77 0 ‐11482.9 D10 ‐5000
11 0 0 0 0 ‐4059.832241 ‐4059.832241 ‐11482.9 0 0 0 15542.77 4059.832 D11 0
12 0 0 0 0 ‐4059.832241 ‐4059.832241 0 0 0 ‐11482.94 4059.832 15542.77 D12 0
6.3E‐07 ΣFx=0 ‐1.59162E‐12
‐6.3E‐07 ΣFy=0 ‐6.82121E‐13
‐1.8E‐12 ΣFx=0 ‐1.36424E‐12
‐1.8E‐12 ΣFy=0 7.27596E‐12
‐1.8E‐12 ΣFx=0 3.18323E‐12
0 ΣFy=0 5.00222E‐12
3.6E‐12 ΣFx=0 ‐6.3443E‐07
0 ΣFy=0 6 3442E‐07ΣF12=0
Constrains
ΣF5=0
ΣF6=0
ΣF7=0
ΣF8=0
joint‐4
joint‐3
Equilibrium Equation in Joints
joint‐1
joint‐2
ΣF9=0
ΣF10=0
ΣF11=0
0 ΣFy=0 6.3442E‐07ΣF12=0

2. >> IN THE NAME OF GOD <<
Pratt Truss Optimization with EXCEL Solver
This program is written by Salar Delavar Ghashghaei ‐ 12/February/2017
Email: salar.d.ghashghaei@gmail.com
15201.46
Min Max
h= 100 100 500 D3= 0.3429
A1= 1.002083 1 30 D4= ‐2.7764
A2= 1 1 30 D5= 0.6857
A3= 2.167014 1 30 D6= ‐2.1246
A4= 2.167014 1 30 D7= 1.0286
A5= 4.633333 1 30 D8= ‐2.6902
A6= 4.394444 1 30 D9= 1.3714
A7= 1 1 30 D11= 0.9119
A8= 1 1 30 D12= ‐2.7766
A9= 1 1 30 D13= 1.2547
A10= 2.394769 1 30 D14= ‐2.124
A11= 2.338113 1 30 D15= 0.9119
A12= 7.222189 1 30 D16= ‐2.6906
A13= 2.203555 1 30
L= 500 5
0.6
F.S 1.667
x y x y 0.6Fy node coordinate-X coordinate-Y Px Py Ux Uy
1 500 0 0 500 0 1.002083333 2100000 2400 1443 1440 1440 1 1 0 0 1 2 0 0
2 500 500 0 1000 0 1 2100000 2400 1440 1440 1440 1 2 500 0 3 4 0.343 ‐2.776
3 500 1000 0 1500 0 2.167013889 2100000 2400 3120.5 1440 1440 1 3 1000 0 5 0 0.686 ‐2.125
4 500 1500 0 2000 0 2.167013889 2100000 2400 3120.5 1440 1440 1 4 1500 0 0 8 1.029 ‐2.690
5 500 500 100 1000 100 4.633333333 2100000 2400 6672 1440 1440 1 5 2000 0 9 10 1.371 0
6 500 1000 100 1500 100 4.394444445 2100000 2400 ‐6328 1440 1440 1 6 500 100 11 12 0.912 ‐2.777
7 100 500 0 500 100 1 2100000 2400 ‐4 4 1440 0 7 1000 100 13000 14 1.255 ‐2.124
8 100 1000 0 1000 100 1 2100000 2400 14 14 1440 0.01 8 1500 100 15 16 0.912 ‐2.691
9 100 1500 0 1500 100 1 2100000 2400 ‐8 8 1440 0.01
10 509.902 0 0 500 100 2.394768679 2100000 2400 3448.467 1440 1440 1 node reaction
11 509.902 500 100 1000 0 2.338112906 2100000 2400 ‐3366.88 1440 1440 1 1-x ‐4.826
12 509.902 1000 0 1500 100 7.222189243 2100000 2400 3295.496 456.3016 1440 0.32 1-y ‐0.678
13 509.902 1500 100 2000 0 10 2100000 2400 ‐3173.12 1440 1440 1 5-y 0.612
1 2 3 4
lanada-x 1 landa-y 0 4208.75
4208.75 0 ‐4208.75 0 1 1 2 3 4 0
0 0 0 0 1 2 q1= ‐4208.75 0 4208.75 0 0 = 1443
‐4208.75 0 4208.75 0 3 0.342857
0 0 0 0 4 ‐2.776404
3 4 5 6
lanada-x 1 landa-y 0 4200
4200 0 ‐4200 0 3 3 4 5 6 0.342857
0 0 0 0 2 4 q2= ‐4200 0 4200 0 ‐2.776404 = 1440
‐4200 0 4200 0 5 0.685714
0 0 0 0 6 ‐2.124618
5 6 7 8
lanada-x 1 landa-y 0 9101.458
9101.458 0 ‐9101.46 0 5 5 6 7 8 0.685714
0 0 0 0 3 6 q3= ‐9101.458 0 9101.46 0 ‐2.124618 = 3120.500001
‐9101.46 0 9101.458 0 7 1.028571
0 0 0 0 8 ‐2.690173
7 8 9 10
lanada-x 1 landa-y 0 9101.458
9101.458 0 ‐9101.46 0 7 7 8 9 10 1.028571
0 0 0 0 4 8 q4= ‐9101.458 0 9101.46 0 ‐2.690173 = 3120.500001
‐9101.46 0 9101.458 0 9 1.371429
0 0 0 0 10 0
11 12 13 14
lanada-x 1 landa-y 0 19460
19460 0 ‐19460 0 11 11 12 13 14 0.91189
0 0 0 0 5 12 q5= ‐19460 0 19460 0 ‐2.776595 = 6671.999999
‐19460 0 19460 0 13 1.254748
0 0 0 0 14 ‐2.123951
13 14 15 16
lanada-x 1 landa-y 0 18456.67
18456.67 0 ‐18456.7 0 13 13 14 15 16 1.254748
0 0 0 0 6 14 q6= ‐18456.67 0 18456.7 0 ‐2.123951 = -6328.000001
‐18456.7 0 18456.67 0 15 0.91189
0 0 0 0 16 ‐2.690553
3 4 11 12
lanada-x 0 landa-y 1 21000
0 0 0 0 3 3 4 11 12 0.342857
0 21000 0 ‐21000 7 4 q7= 0 ‐21000 0 21000 ‐2.776404 = -4
Target Function
weight
Fy P P/A
Define Scale Factor to show Deformation :
stress ratio
m
emb er L
start end
A E
‐40
‐20
0
20
40
60
80
100
‐500 0 500 1000 1500 2000 2500
4*L
2
1
4
3
16
15
14
13
10
9
8
7
6
5
12
11
h
4*L

3. >> IN THE NAME OF GOD <<
Pratt Truss Optimization with EXCEL Solver
This program is written by Salar Delavar Ghashghaei ‐ 12/February/2017
Email: salar.d.ghashghaei@gmail.com
0 0 0 0 11 0.91189
0 ‐21000 0 21000 12 ‐2.776595
5 6 13 14
lanada-x 0 landa-y 1 21000
0 0 0 0 5 5 6 13 14 0.685714
0 21000 0 ‐21000 8 6 q8= 0 ‐21000 0 21000 ‐2.124618 = 14
0 0 0 0 13 1.254748
0 ‐21000 0 21000 14 ‐2.123951
7 8 15 16
lanada-x 0 landa-y 1 21000
0 0 0 0 7 7 8 15 16 1.028571
0 21000 0 ‐21000 9 8 q9= 0 ‐21000 0 21000 ‐2.690173 = -8
0 0 0 0 15 0.91189
0 ‐21000 0 21000 16 ‐2.690553
1 2 11 12
lanada-x 0.980581 landa-y 0.196116 9862.708
9483.373 1896.675 ‐9483.37 ‐1896.67 1 1 2 11 12 0
1896.675 379.3349 ‐1896.67 ‐379.335 10 2 q10= ‐9671.181 ‐1934.24 9671.18 1934.236 0 = 3448.466897
‐9483.37 ‐1896.67 9483.373 1896.675 11 0.91189
‐1896.67 ‐379.335 1896.675 379.3349 12 ‐2.776595
11 12 5 6
lanada-x 0.980581 landa-y ‐0.19612 9629.375
9259.014 ‐1851.8 ‐9259.01 1851.803 11 11 12 5 6 0.91189
‐1851.8 370.3606 1851.803 ‐370.361 11 12 q11= ‐9442.379 1888.476 9442.38 ‐1888.48 ‐2.776595 = -3366.882585
‐9259.01 1851.803 9259.014 ‐1851.8 5 0.685714
1851.803 ‐370.361 ‐1851.8 370.3606 6 ‐2.124618
5 6 15 16
lanada-x 0.980581 landa-y 0.196116 29744.14
28600.14 5720.028 ‐28600.1 ‐5720.03 5 5 6 15 16 0.685714
5720.028 1144.006 ‐5720.03 ‐1144.01 12 6 q12= ‐29166.53 ‐5833.31 29166.5 5833.307 ‐2.124618 = 3295.496312
‐28600.1 ‐5720.03 28600.14 5720.028 15 0.91189
‐5720.03 ‐1144.01 5720.028 1144.006 16 ‐2.690553
15 16 9 10
lanada-x 0.980581 landa-y ‐0.19612 41184.39
39600.37 ‐7920.07 ‐39600.4 7920.075 15 15 16 9 10 0.91189
‐7920.07 1584.015 7920.075 ‐1584.01 13 16 q13= ‐40384.62 8076.923 40384.6 ‐8076.92 ‐2.690553 = -3173.119844
‐39600.4 7920.075 39600.37 ‐7920.07 9 1.371429
7920.075 ‐1584.01 ‐7920.07 1584.015 10 0
1 2 10 3 4 5 6 7 8 9 11 12 13 14 15 16
1 13692.12 1896.675 0 ‐4208.75 0 0 0 0 0 0 ‐9483.37 ‐1896.675 0 0 0 0 0 Q1
2 1896.675 379.3349 0 0 0 0 0 0 0 0 ‐1896.67 ‐379.3349 0 0 0 0 0 Q2
10 0 0 1584.015 0 0 0 0 0 0 ‐7920.07 0 0 0 0 7920.075 ‐1584.01 0 Q10
3 ‐4208.75 0 0 8408.75 0 ‐4200 0 0 0 0 0 0 0 0 0 0 D3 3
4 0 0 0 0 21000 0 0 0 0 0 0 ‐21000 0 0 0 0 D4 4
5 0 0 0 ‐4200 0 51161 0 ‐9101.46 0 0 ‐9259.01 1851.803 0 0 ‐28600.1 ‐5720.03 D5 5
6 0 0 0 0 0 3868.2 22514.37 0 0 0 1851.803 ‐370.3606 0 ‐21000 ‐5720.03 ‐1144.01 D6 0
7 0 0 0 0 0 ‐9101.5 0 18202.92 0 ‐9101.46 0 0 0 0 0 0 X D7 = 0
8 0 0 0 0 0 0 0 0 21000 0 0 0 0 0 0 ‐21000 D8 8
9 0 0 ‐7920.07 0 0 0 0 ‐9101.46 0 48701.83 0 0 0 0 ‐39600.4 7920.075 D9 9
11 ‐9483.37 ‐1896.67 0 0 0 ‐9259 1851.803 0 0 0 38202.39 44.87179 ‐19460 0 0 0 D11 11
12 ‐1896.67 ‐379.335 0 0 ‐21000 1851.8 ‐370.3606 0 0 0 44.87179 21749.7 0 0 0 0 D12 12
13 0 0 0 0 0 0 0 0 0 0 ‐19460 0 37916.67 0 ‐18456.7 0 D13 13000
14 0 0 0 0 0 0 ‐21000 0 0 0 0 0 0 21000 0 0 D14 14
15 0 0 7920.075 0 0 ‐28600 ‐5720.028 0 0 ‐39600.4 0 0 ‐18456.7 0 86657.18 ‐2200.05 D15 15
16 0 0 ‐1584.01 0 0 ‐5720 ‐1144.006 0 ‐21000 7920.075 0 0 0 0 ‐2200.05 23728.02 D16 16
D3 0.3429
D4 ‐2.7764
D5 0.6857
D6 ‐2.1246 0
D7 1.0286 0
D8 ‐2.6902 Q1 ‐4825.5 1.79E‐07
D9 = 1.3714 Q2 = ‐678.3 7.16E‐08
D11 0.9119 Q10 612.3 5.46E‐12
D12 ‐2.7766 ‐7.3E‐12
D13 1.2547 0
D14 ‐2.124 ‐3.6E‐12
D15 0.9119 1.46E‐11
D16 ‐2.6906 0
0
‐3.6E‐07
‐7.2E‐08
Constrains
ΣF3=0
ΣF4=0
ΣF5=0
ΣF6=0
ΣF7=0
ΣF8=0
ΣF9=0
ΣF11=0
ΣF12=0
ΣF13=0
ΣF14=0
ΣF15=0
ΣF16=0