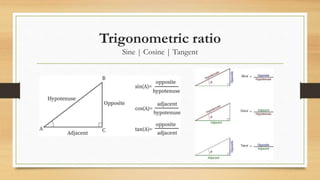
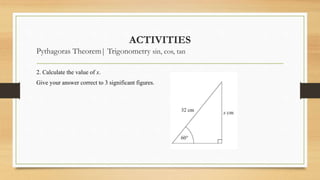
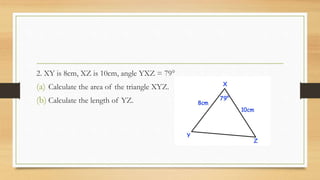
1) The document discusses trigonometry and solving right triangles using Pythagorean theorem, trigonometric ratios (sine, cosine, tangent), sine rule, and cosine rule. 2) Examples are provided to use these concepts to calculate missing side lengths and angles of right triangles given various inputs. 3) Activities at the end instruct students to solve additional right triangle problems applying these trigonometry concepts.

1. TRIGONOMETRY
Monday 27th September 2022

2. Reminder
• The longest side is called the hypotenuse
• a2 + b2 = c2

3. From previous class
PYTHAGORAS THEOREM
1. PQR is a right-angled triangle. PQ = 16 cm. PR = 8 cm.
Calculate the length of QR.
Give your answer correct to 2 decimal places.
2. XYZ is a right-angled triangle. XY = 3.2 cm. XZ = 1.7 cm.
Calculate the length of YZ.
Give your answer correct to 3 significant figures
8cm
Q
p
16cm
R
X Y
Z
1.7cm
3.2cm

5. Trigonometric ratio
Sine | Cosine | Tangent

6. • These, along with Pythagoras theorem, allow us solve problems involving
right-angled triangles.
Note: These definitions apply only to angles less than 900 (Q < 900 )
SOH CAH TOA
Sine Cosine Tangent

7. Examples
• ABC is a right-angled triangle. Angle B = 900.
Angle A = 360. AB = 8.7 cm.
Work out the length of BC.
• Give your answer correct to 3 significant figures.

8. LMN is a right-angled triangle. MN = 9.6 cm.
LM = 6.4 cm. Calculate the size of the angle marked x0.
• Give your answer correct to 1 decimal place.
Examples

9. ACTIVITIES
Pythagoras Theorem| Trigonometry sin, cos, tan
1. A rectangular television screen has a width of 45 cm and a height of 34 cm.
Work out the length of the diagonal of the screen.
Give your answer correct to the nearest centimetre

10. 2. Calculate the value of x.
Give your answer correct to 3 significant figures.
ACTIVITIES
Pythagoras Theorem| Trigonometry sin, cos, tan

11. Sine Rule
a) two angles and one side
b) two sides and a non-included angle
• Study the triangle ABC shown below. Let B stands for the angle at B. Let C
stand for the angle at C and so on. Also, let b = AC, a = BC and c = AB.
• The sine rule : 𝐚
𝐬𝐢𝐧 𝐀
=
𝐛
𝐬𝐢𝐧 𝐁
=
𝐂
𝐬𝐢𝐧 𝐂

12. Cosine Rule
a) three sides
b) two sides and the included angle.
The cosine rule:
• a2 = b2 + c2 − 2bc cosA,
• b2 = a2 + c2 − 2ac cosB,
• c2 = a2 + b2 − 2ab cosC

13. Examples
1. In triangle ABC, AB = 42cm, BC = 37cm and AC = 26cm. Solve this
triangle.
2. Solve the triangle ABC in which AC = 105cm, AB = 76cm and A = 29◦

15. Activities
1. Calculate the size of the angle labelled y.
2. Solve the triangle ABC given C = 40◦, b = 23cm and c = 19cm.

17. Activities
1. Find the size of x.

18. 2. XY is 8cm, XZ is 10cm, angle YXZ = 79°
(a) Calculate the area of the triangle XYZ.
(b) Calculate the length of YZ.