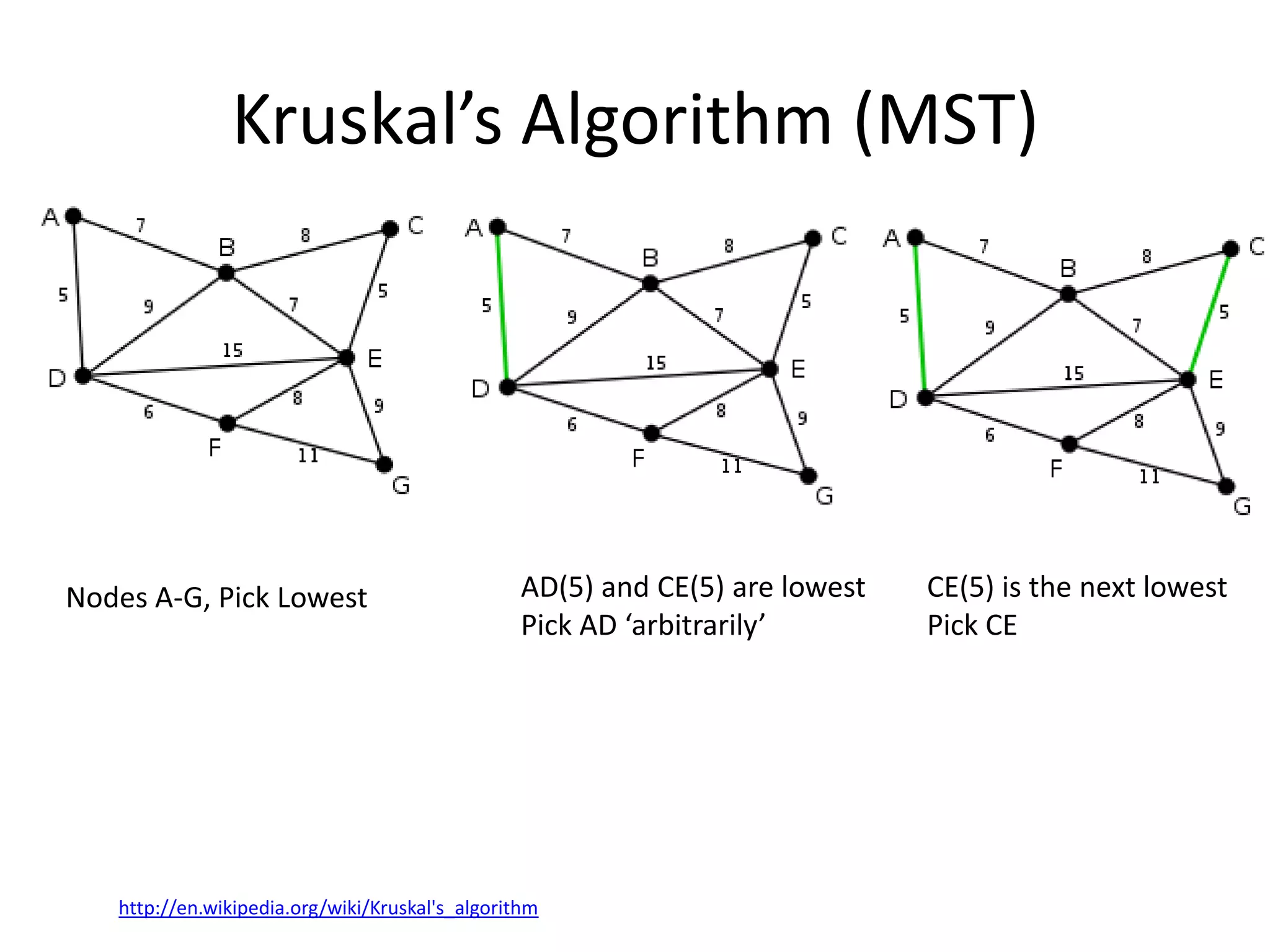
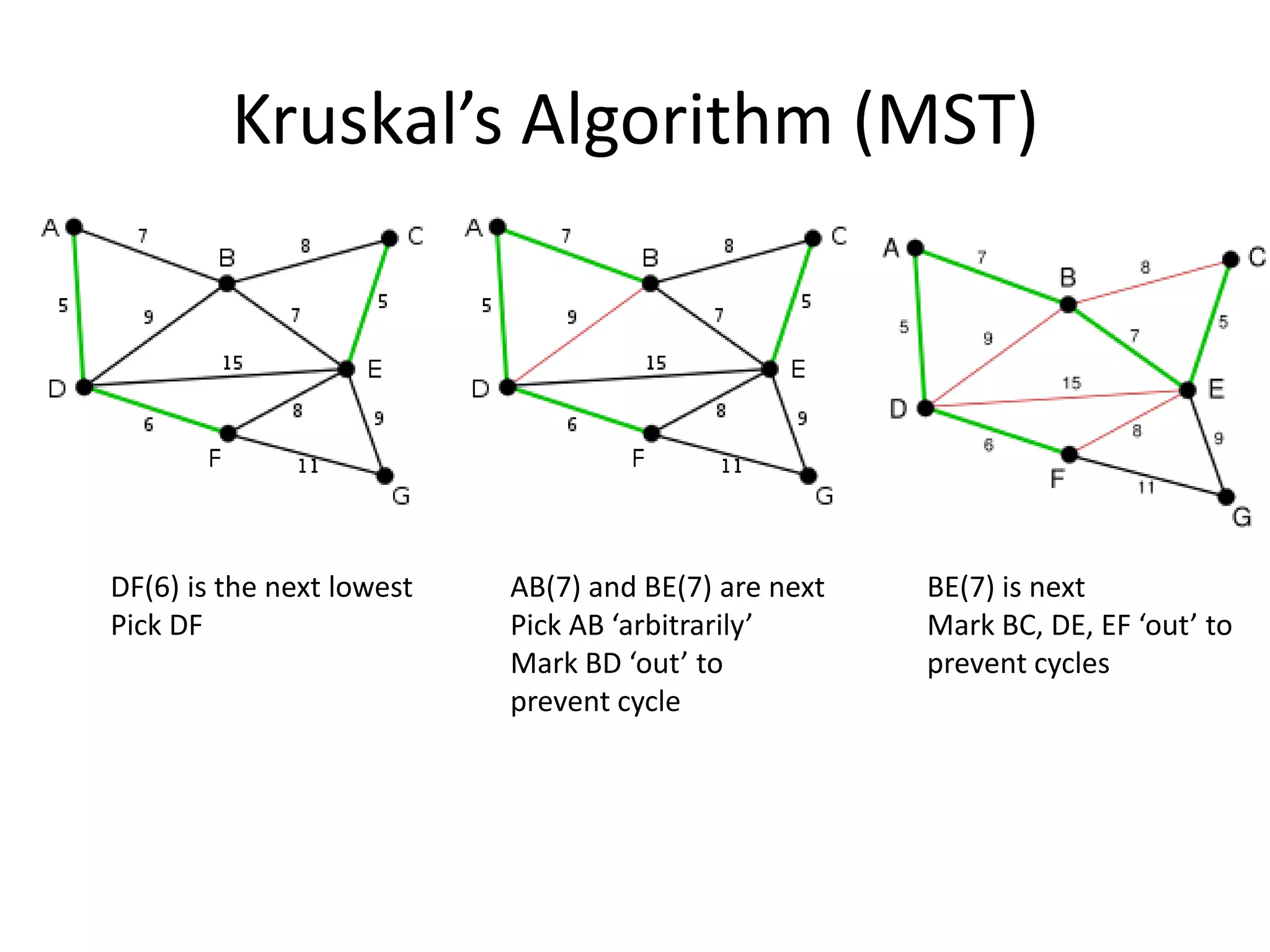
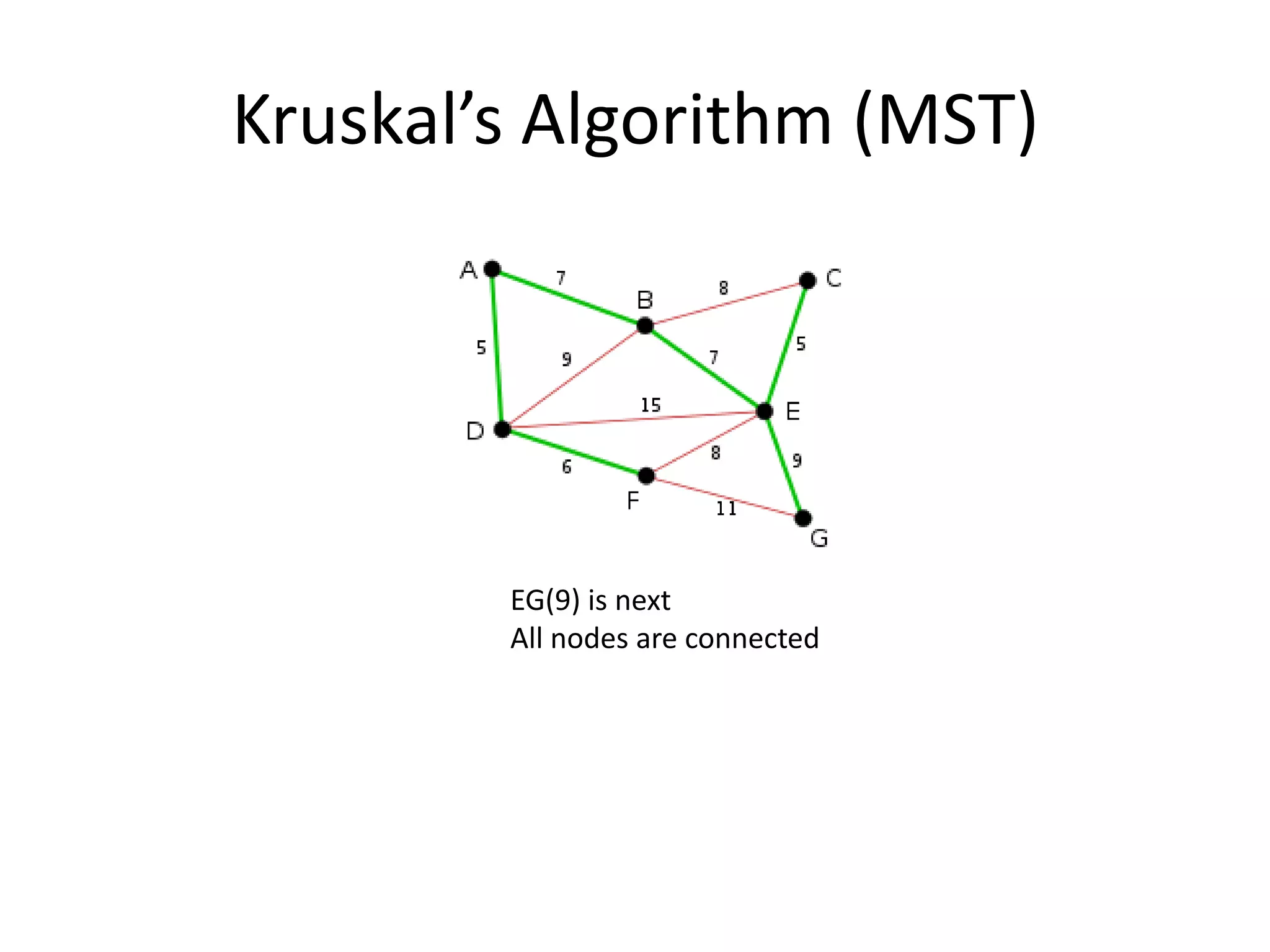
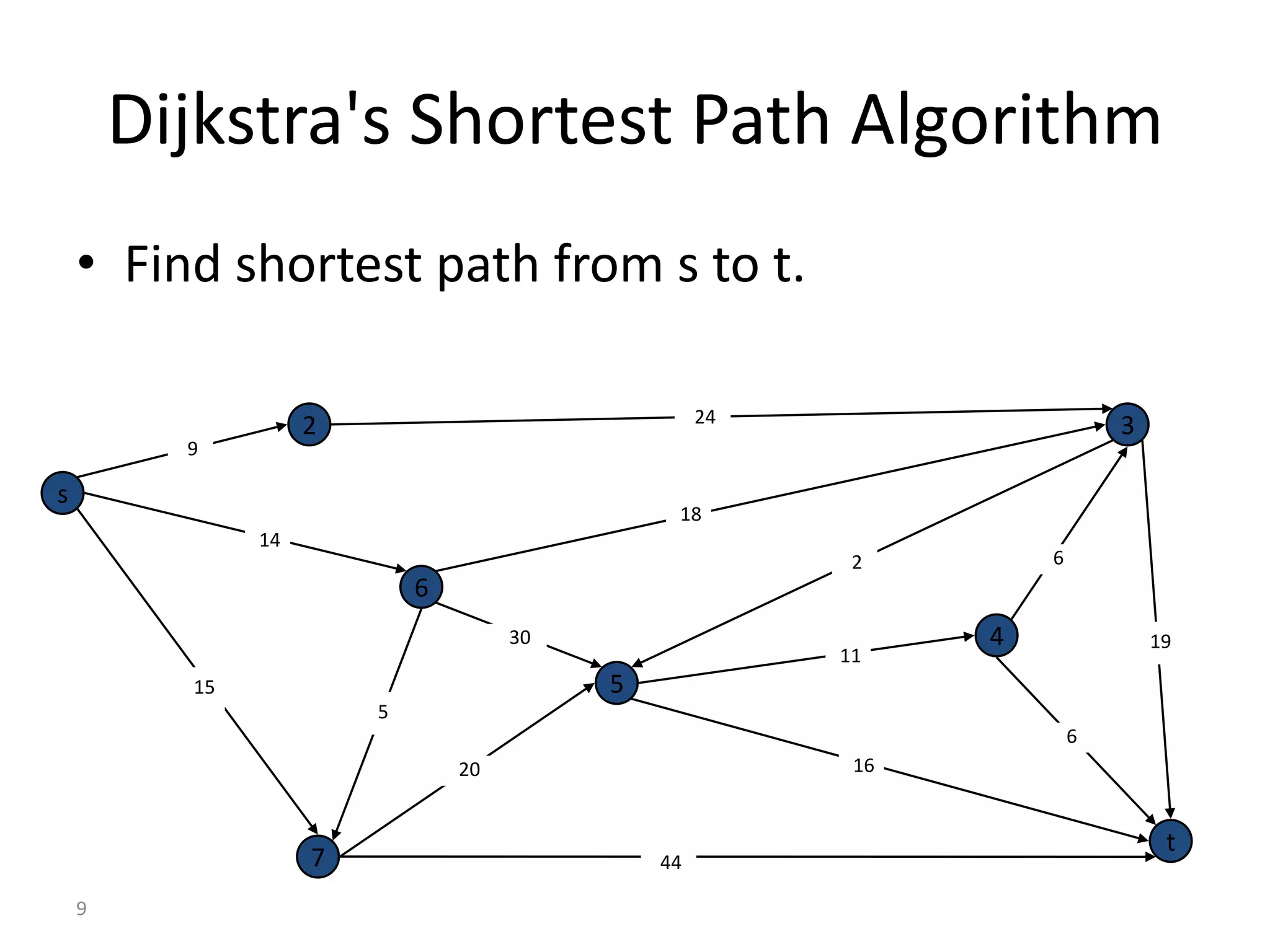
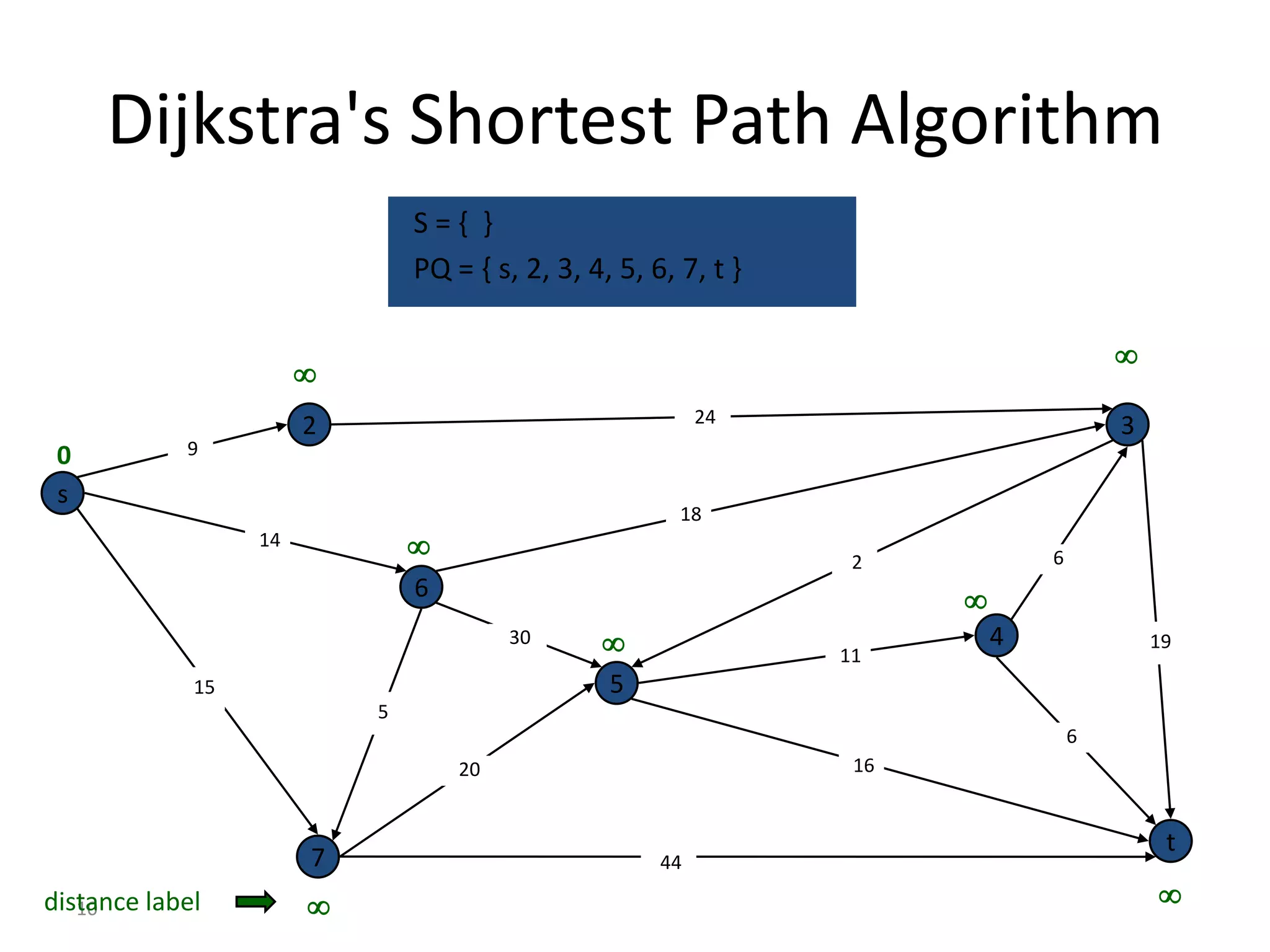
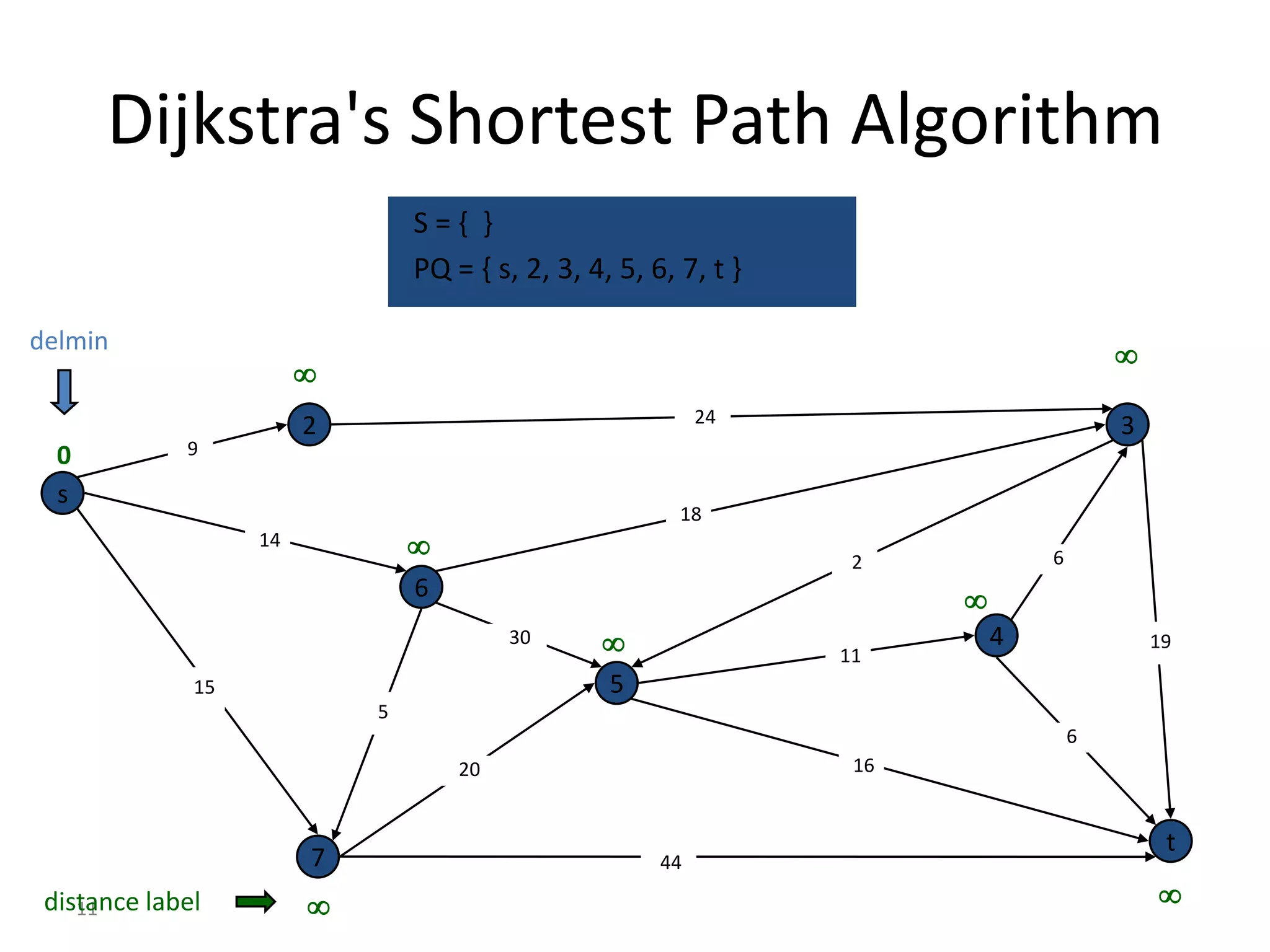
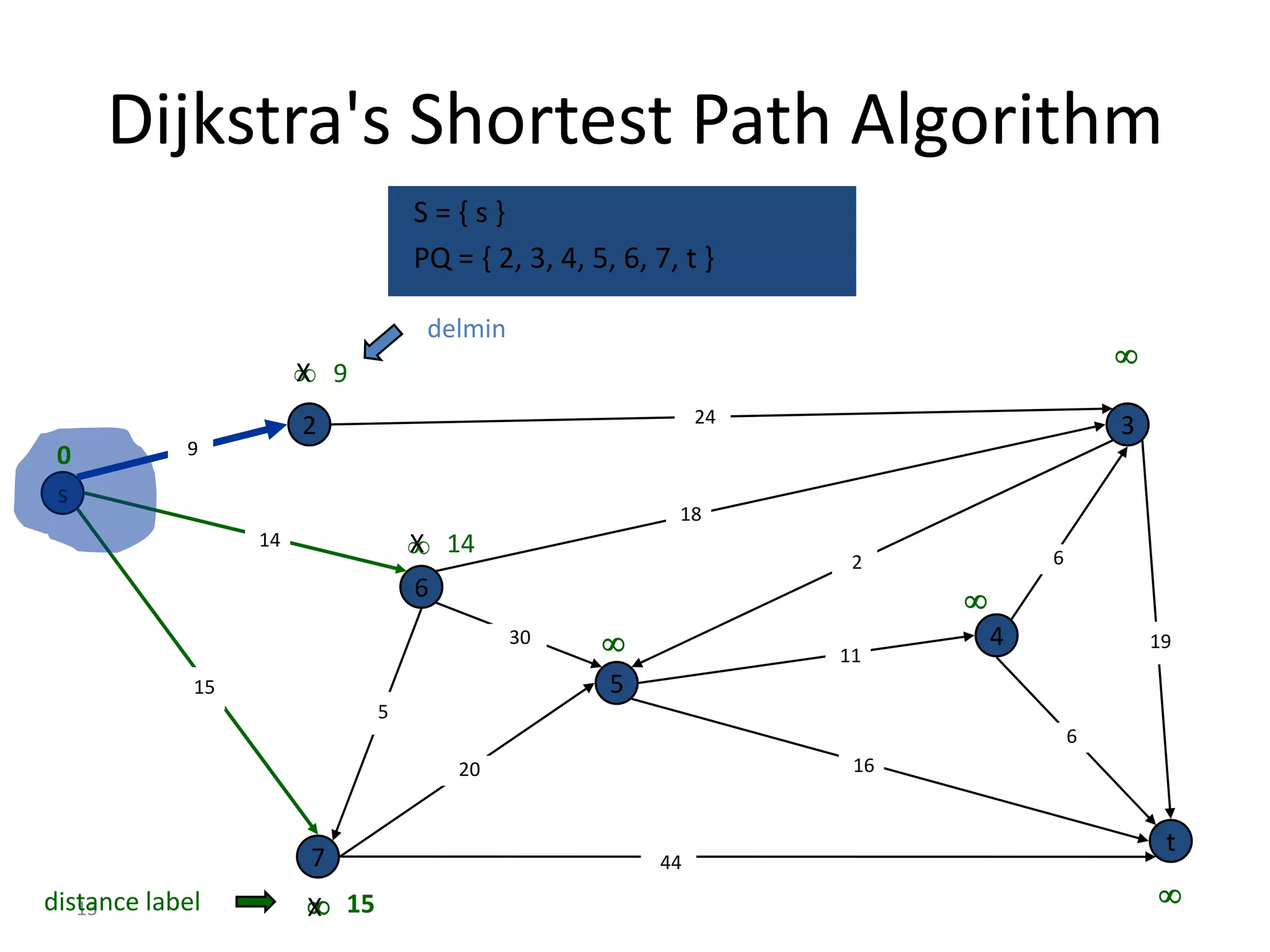
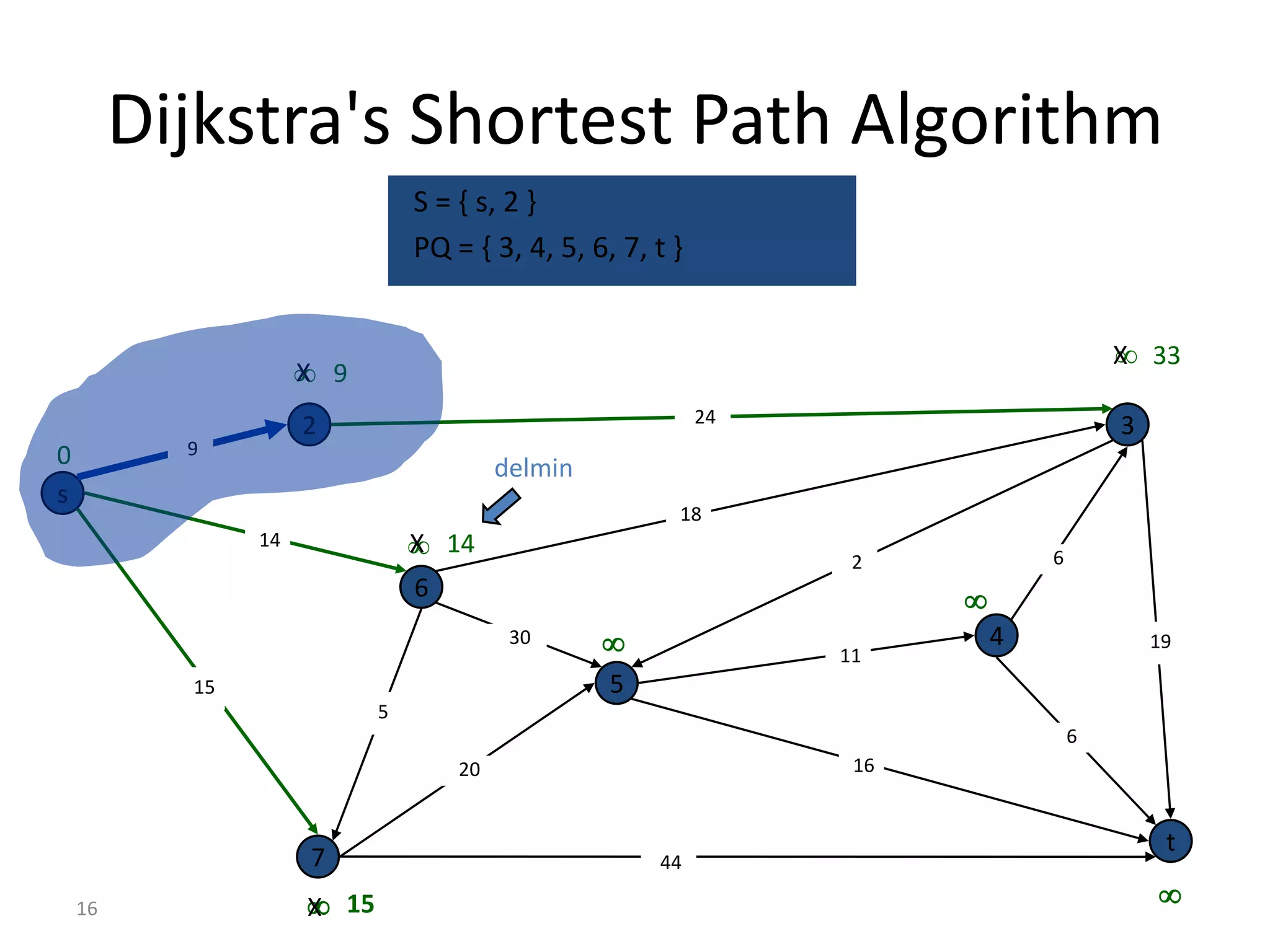
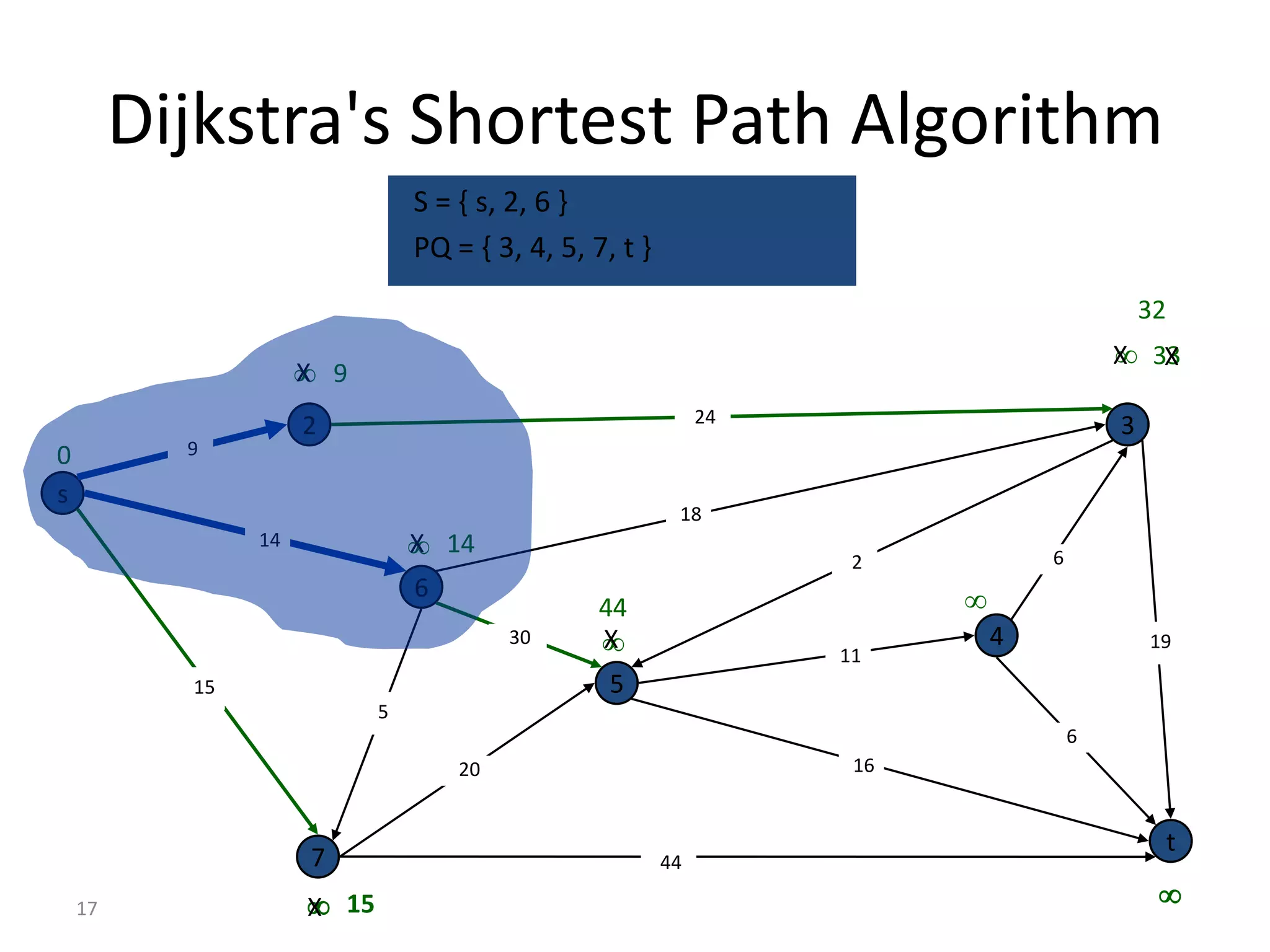
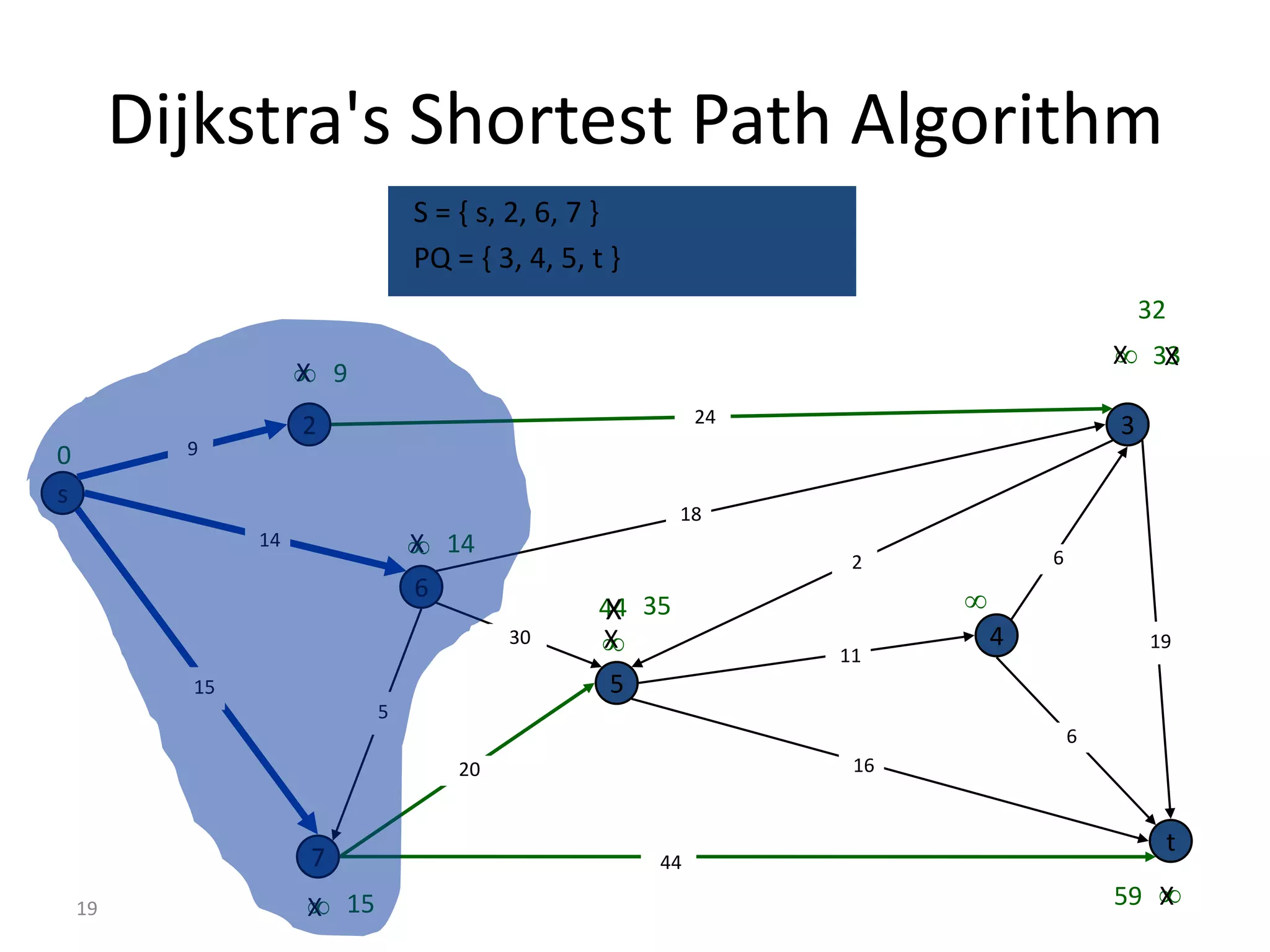
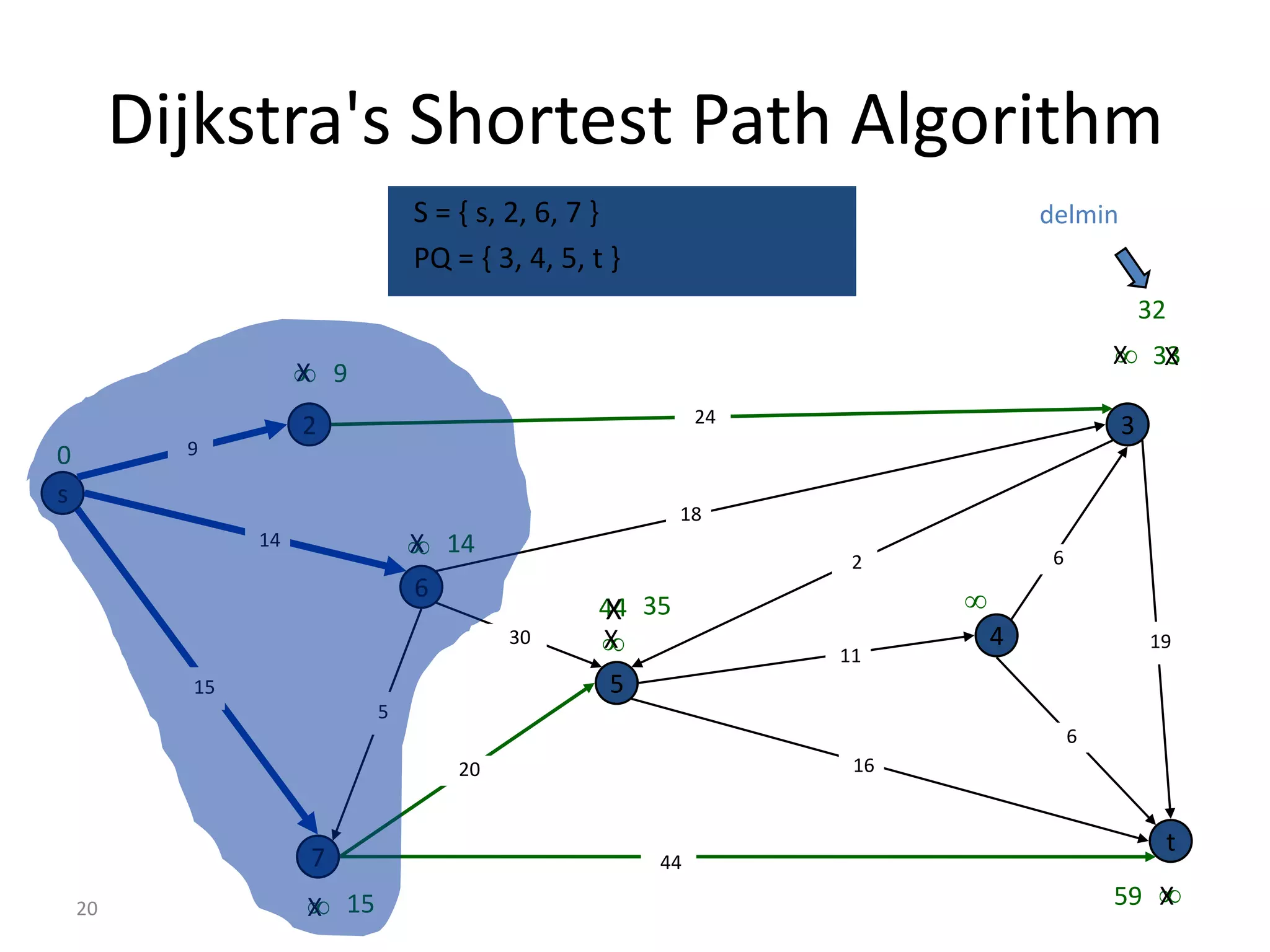
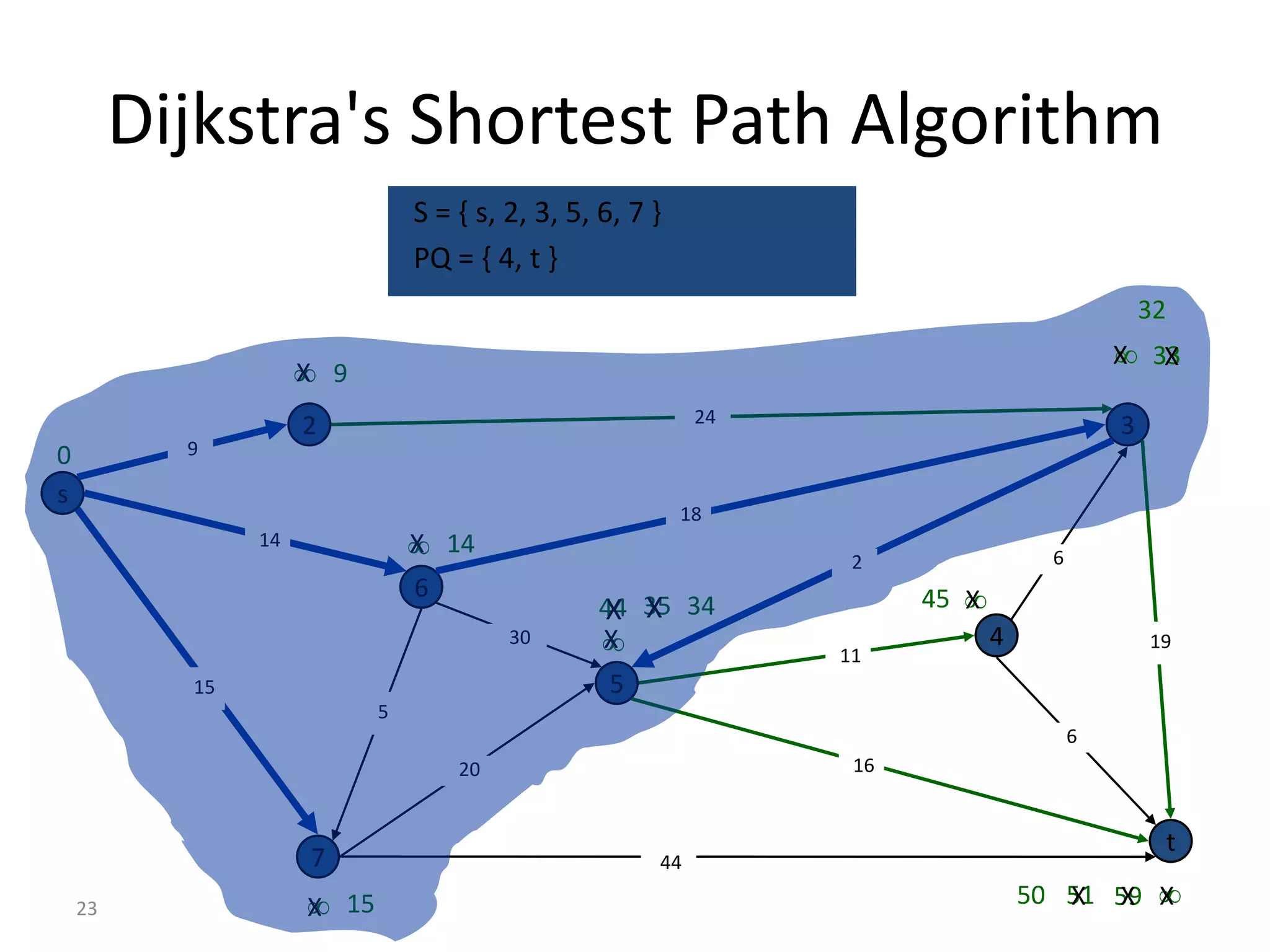
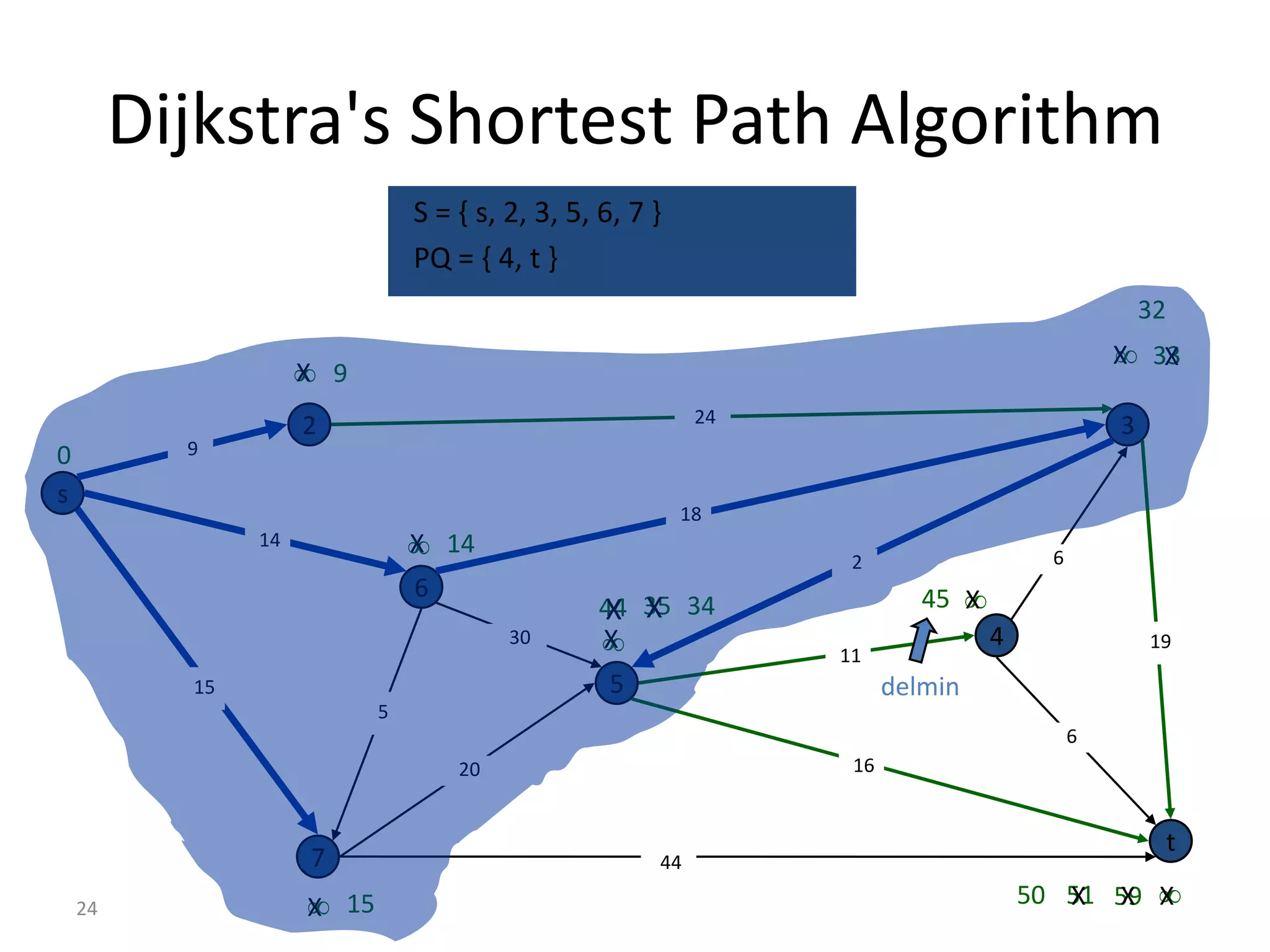
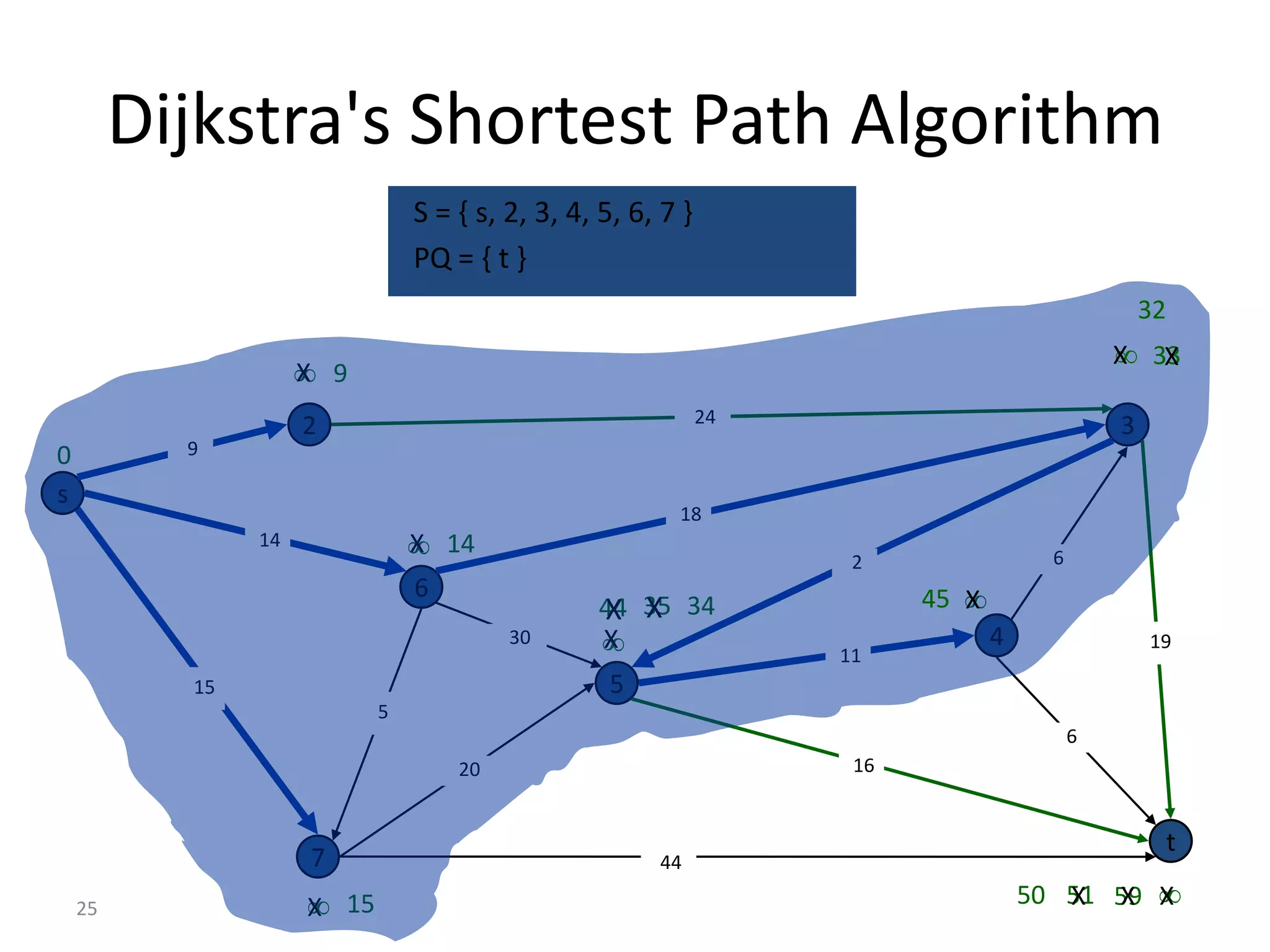
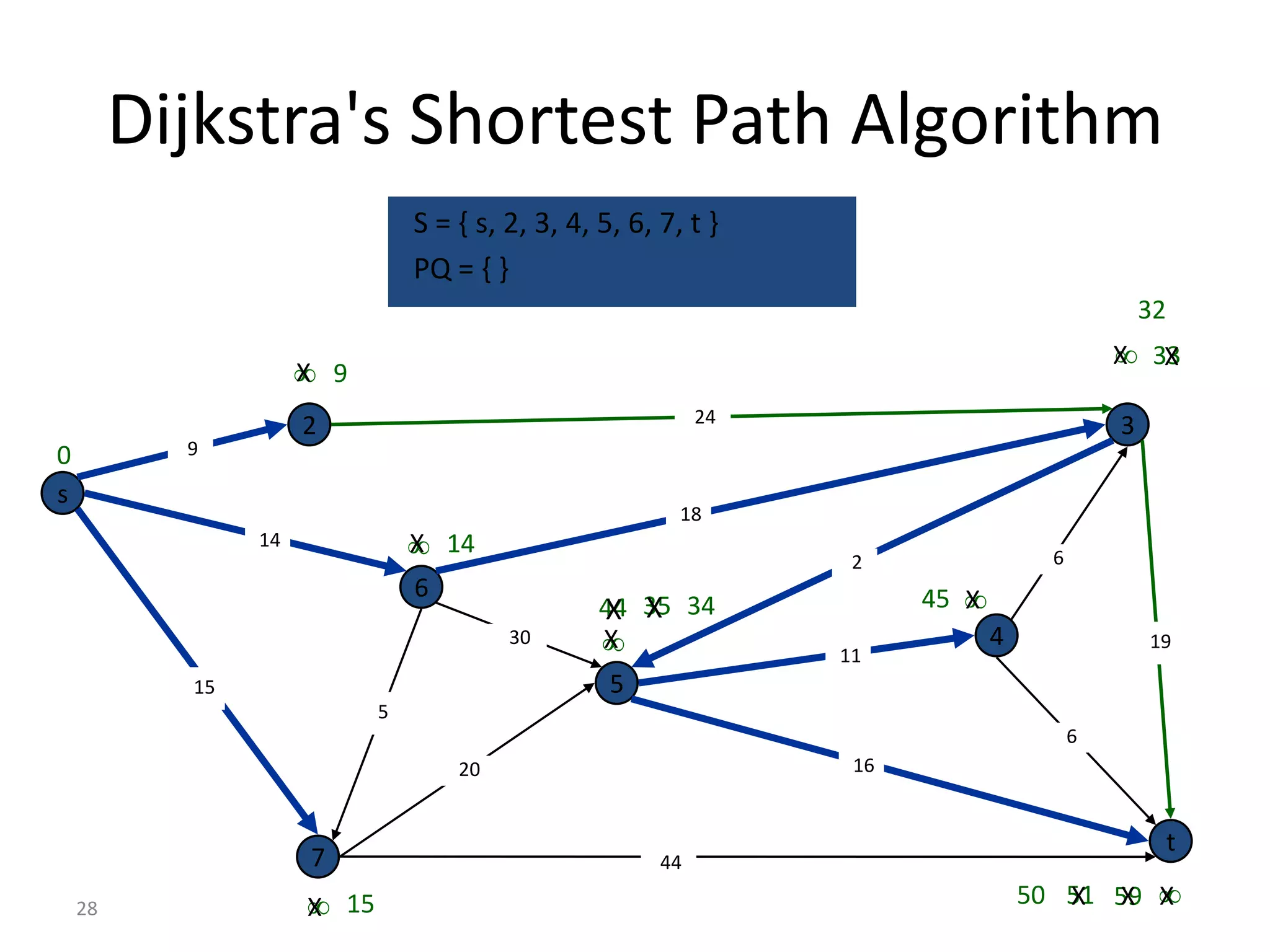
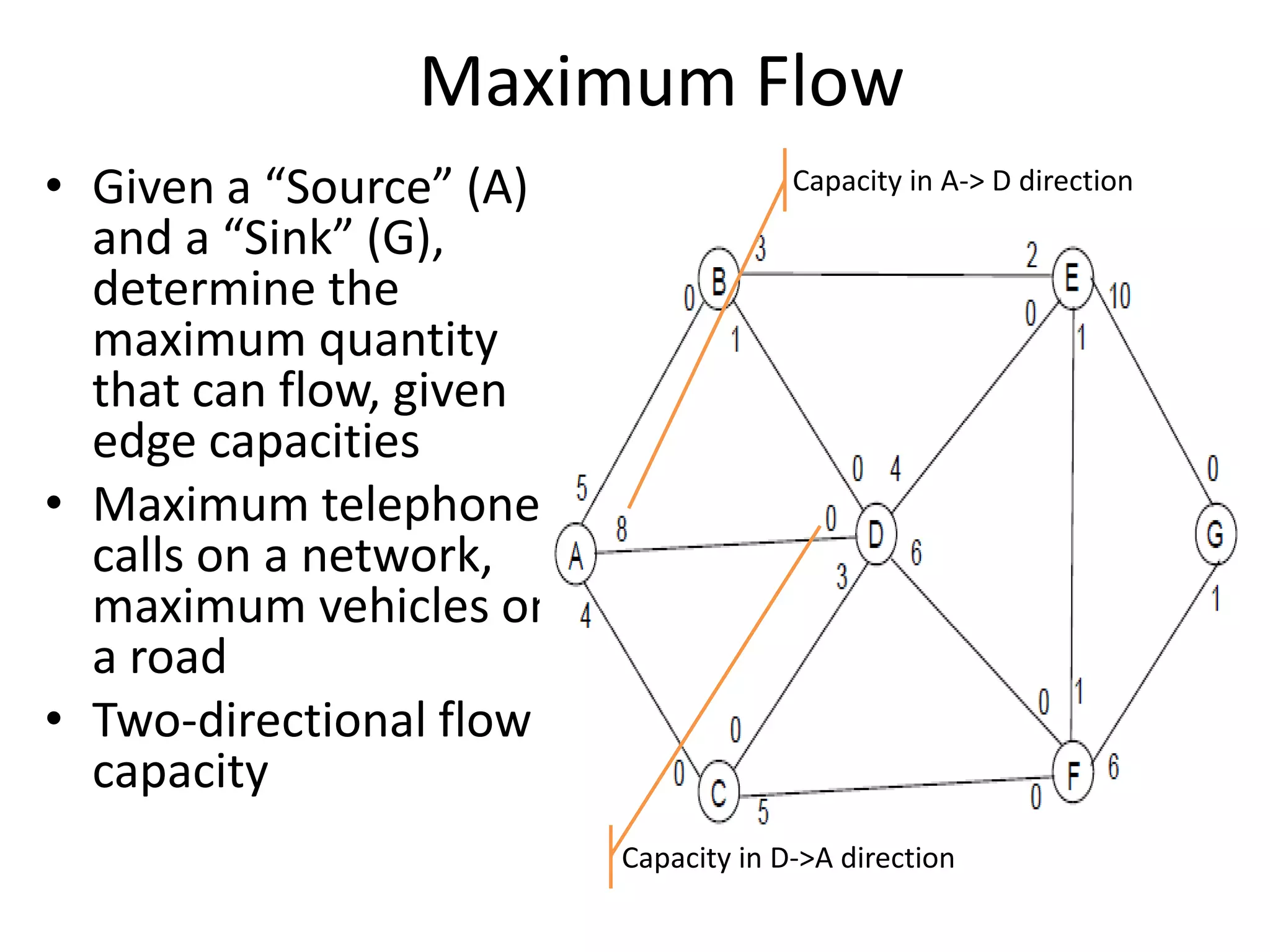
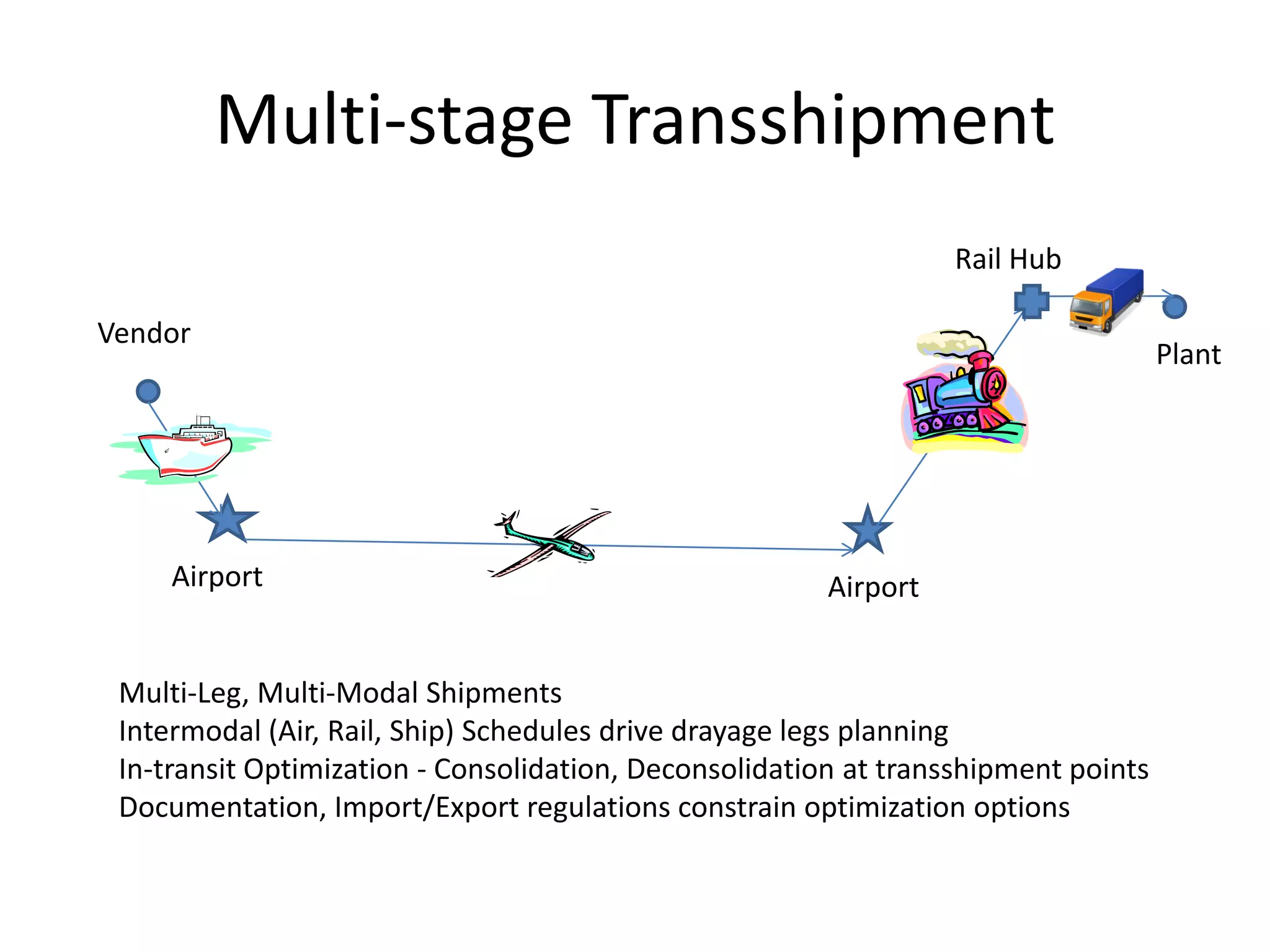
The document discusses various algorithms for solving transportation network models, including minimal spanning tree algorithms like Kruskal's and Prim's, shortest path algorithms like Dijkstra's and Floyd-Warshall, and maximal flow algorithms. It provides examples and step-by-step explanations of how Kruskal's and Dijkstra's algorithms work to find minimal spanning trees and shortest paths in graphs. Transportation network models have applications in logistics for routing vehicles and scheduling deliveries.

1. Postgraduate Certificate in Logistics &
Supply Chain Management (PGCLSCM)
Transportation Network Models

2. Topics covered
• Notion of Graphs (Friday-I)
• Minimal Spanning Tree (Friday-I)
• Shortest Path Algorithms (Friday-I)
• Maximal Flow (Friday-II)
• Multistage Transshipment (Friday-II)
• Set covering and Set Partitioning (Friday-II)
• Routing Heuristics and Optimization (Sunday-I)
• Case Study – Model the Location Constraints problem
(Sunday-II)

3. Graphs – Terminology Revision
• Vertices, Nodes, Edges
• Undirected, Directed, Bi-directed, Mixed
(Undirected/directed edges), Loops (on the same
node/vertex), Multi-Graph (multiple edges between the
same nodes), Weighted
• Complete graph, Cycle graph, Planar graph (no edges
intersect), tree (undirected graph with a single path
between any two notes)
• Subgraphs, connected, isolated
http://en.wikipedia.org/wiki/Graph_theory

4. Minimal Spanning Tree(MST)
• Span ALL Nodes, Pick Lowest Cost Edges
• Prim‟s and Kruskal‟s algorithm (Concept of greedy
algorithm)
• Variants - Maximum Spanning tree, K-minimum spanning
tree
• Applications – Selecting Service Providers across multiple
offices (each edge with different cost/charges), Laying
phone lines, pipelines, Contract Rate/Carrier negotiations

5. Kruskal‟s Algorithm (MST)
Nodes A-G, Pick Lowest AD(5) and CE(5) are lowest CE(5) is the next lowest
Pick AD ‘arbitrarily’ Pick CE
http://en.wikipedia.org/wiki/Kruskal's_algorithm

6. Kruskal‟s Algorithm (MST)
DF(6) is the next lowest AB(7) and BE(7) are next BE(7) is next
Pick DF Pick AB ‘arbitrarily’ Mark BC, DE, EF ‘out’ to
Mark BD ‘out’ to prevent cycles
prevent cycle

7. Kruskal‟s Algorithm (MST)
EG(9) is next
All nodes are connected

8. Shortest Path
• Pick Lowest Cost traversal between two nodes
• Dijkstra (From single source to all other nodes)
• Floyd-Warshall (Single execution finds shortest path for all
node pairs in the graph)
• Travelling Salesman (Travel to every node exactly once and
return to the start node)
• Canadian Traveler Problem (Graph unknown, changes over
time, is probabilistic)
• Applications – Driving directions (google), Plant/Warehouse
layouts, robotics/VLSI

9. Dijkstra's Shortest Path Algorithm
• Find shortest path from s to t.
24
2 3
9
s
18
14
2 6
6
30 4 19
11
15 5
5
6
20 16
t
7 44
9

10. Dijkstra's Shortest Path Algorithm
S={ }
PQ = { s, 2, 3, 4, 5, 6, 7, t }


24
2 3
0 9
s
18
14  2 6
6 
30  11
4 19
15 5
5
6
20 16
t
7 44
distance label  10

11. Dijkstra's Shortest Path Algorithm
S={ }
PQ = { s, 2, 3, 4, 5, 6, 7, t }
delmin


24
2 3
0 9
s
18
14  2 6
6 
30  11
4 19
15 5
5
6
20 16
t
7 44
distance label  11

12. Dijkstra's Shortest Path Algorithm
S={s}
PQ = { 2, 3, 4, 5, 6, 7, t }
decrease key

 9
X
24
2 3
0 9
s
18
14  14
X
2 6
6 
30  11
4 19
15 5
5
6
20 16
t
7 44
distance label  15
X 12

13. Dijkstra's Shortest Path Algorithm
S={s}
PQ = { 2, 3, 4, 5, 6, 7, t }
delmin

 9
X
24
2 3
0 9
s
18
14  14
X
2 6
6 
30  11
4 19
15 5
5
6
20 16
t
7 44
distance label  15
X 13

14. Dijkstra's Shortest Path Algorithm
S = { s, 2 }
PQ = { 3, 4, 5, 6, 7, t }

 9
X
24
2 3
0 9
s
18
14  14
X
2 6
6 
30  11
4 19
15 5
5
6
20 16
t
7 44
 15
X 14

15. Dijkstra's Shortest Path Algorithm
S = { s, 2 }
PQ = { 3, 4, 5, 6, 7, t }
decrease key

X 33
 9
X
24
2 3
0 9
s
18
14  14
X
2 6
6 
30  11
4 19
15 5
5
6
20 16
t
7 44
 15
X 15

16. Dijkstra's Shortest Path Algorithm
S = { s, 2 }
PQ = { 3, 4, 5, 6, 7, t }

X 33
 9
X
24
2 3
0 9
delmin
s
18
14  14
X
2 6
6 
30  11
4 19
15 5
5
6
20 16
t
7 44
 15
X 16

17. Dijkstra's Shortest Path Algorithm
S = { s, 2, 6 }
PQ = { 3, 4, 5, 7, t }
32
 X
X 33
 9
X
24
2 3
0 9
s
18
14  14
X
2 6
6 
44
30 
X
11
4 19
15 5
5
6
20 16
t
7 44
 15
X 17

18. Dijkstra's Shortest Path Algorithm
S = { s, 2, 6 }
PQ = { 3, 4, 5, 7, t }
32
 X
X 33
 9
X
24
2 3
0 9
s
18
14  14
X
2 6
6 
44
30 
X
11
4 19
15 5
5
6
20 16
t
7 44
 15
X delmin 18

19. Dijkstra's Shortest Path Algorithm
S = { s, 2, 6, 7 }
PQ = { 3, 4, 5, t }
32
 X
X 33
 9
X
24
2 3
0 9
s
18
14  14
X
2 6
6 
44 35
X
30 
X
11
4 19
15 5
5
6
20 16
t
7 44
 15
X 59 
X19

20. Dijkstra's Shortest Path Algorithm
S = { s, 2, 6, 7 } delmin
PQ = { 3, 4, 5, t }
32
 X
X 33
 9
X
24
2 3
0 9
s
18
14  14
X
2 6
6 
44 35
X
30 
X
11
4 19
15 5
5
6
20 16
t
7 44
 15
X 59 
X20

21. Dijkstra's Shortest Path Algorithm
S = { s, 2, 3, 6, 7 }
PQ = { 4, 5, t }
32
 X
X 33
 9
X
24
2 3
0 9
s
18
14  14
X
2 6
6 
44 35 34
X X
30 
X
11
4 19
15 5
5
6
20 16
t
7 44
 15
X 51 59 
X X21

22. Dijkstra's Shortest Path Algorithm
S = { s, 2, 3, 6, 7 }
PQ = { 4, 5, t }
32
 X
X 33
 9
X
24
2 3
0 9
s
18
14  14
X
2 6
6 
44 35 34
X X
30 
X
11
4 19
15 5
5
6
20 16
delmin
t
7 44
 15
X 51 59 
X X22

23. Dijkstra's Shortest Path Algorithm
S = { s, 2, 3, 5, 6, 7 }
PQ = { 4, t }
32
 X
X 33
 9
X
24
2 3
0 9
s
18
14  14
X
2 6
6 45 
X
44 35 34
X X
30 
X
11
4 19
15 5
5
6
20 16
t
7 44
 15
X 50 51 59 
X X X23

24. Dijkstra's Shortest Path Algorithm
S = { s, 2, 3, 5, 6, 7 }
PQ = { 4, t }
32
 X
X 33
 9
X
24
2 3
0 9
s
18
14  14
X
2 6
6 45 
X
44 35 34
X X
30 
X
11
4 19
15 5 delmin
5
6
20 16
t
7 44
 15
X 50 51 59 
X X X24

25. Dijkstra's Shortest Path Algorithm
S = { s, 2, 3, 4, 5, 6, 7 }
PQ = { t }
32
 X
X 33
 9
X
24
2 3
0 9
s
18
14  14
X
2 6
6 45 
X
44 35 34
X X
30 
X
11
4 19
15 5
5
6
20 16
t
7 44
 15
X 50 51 59 
X X X25

26. Dijkstra's Shortest Path Algorithm
S = { s, 2, 3, 4, 5, 6, 7 }
PQ = { t }
32
 X
X 33
 9
X
24
2 3
0 9
s
18
14  14
X
2 6
6 45 
X
44 35 34
X X
30 
X
11
4 19
15 5
5
6
20 16
t
7 44
 15
X
delmin 50 51 59 
X X X26

27. Dijkstra's Shortest Path Algorithm
S = { s, 2, 3, 4, 5, 6, 7, t }
PQ = { }
32
 X
X 33
 9
X
24
2 3
0 9
s
18
14  14
X
2 6
6 45 
X
44 35 34
X X
30 
X
11
4 19
15 5
5
6
20 16
t
7 44
 15
X 50 51 59 
X X X27

28. Dijkstra's Shortest Path Algorithm
S = { s, 2, 3, 4, 5, 6, 7, t }
PQ = { }
32
 X
X 33
 9
X
24
2 3
0 9
s
18
14  14
X
2 6
6 45 
X
44 35 34
X X
30 
X
11
4 19
15 5
5
6
20 16
t
7 44
 15
X 50 51 59 
X X X28

29. Floyd-Warshall algorithm

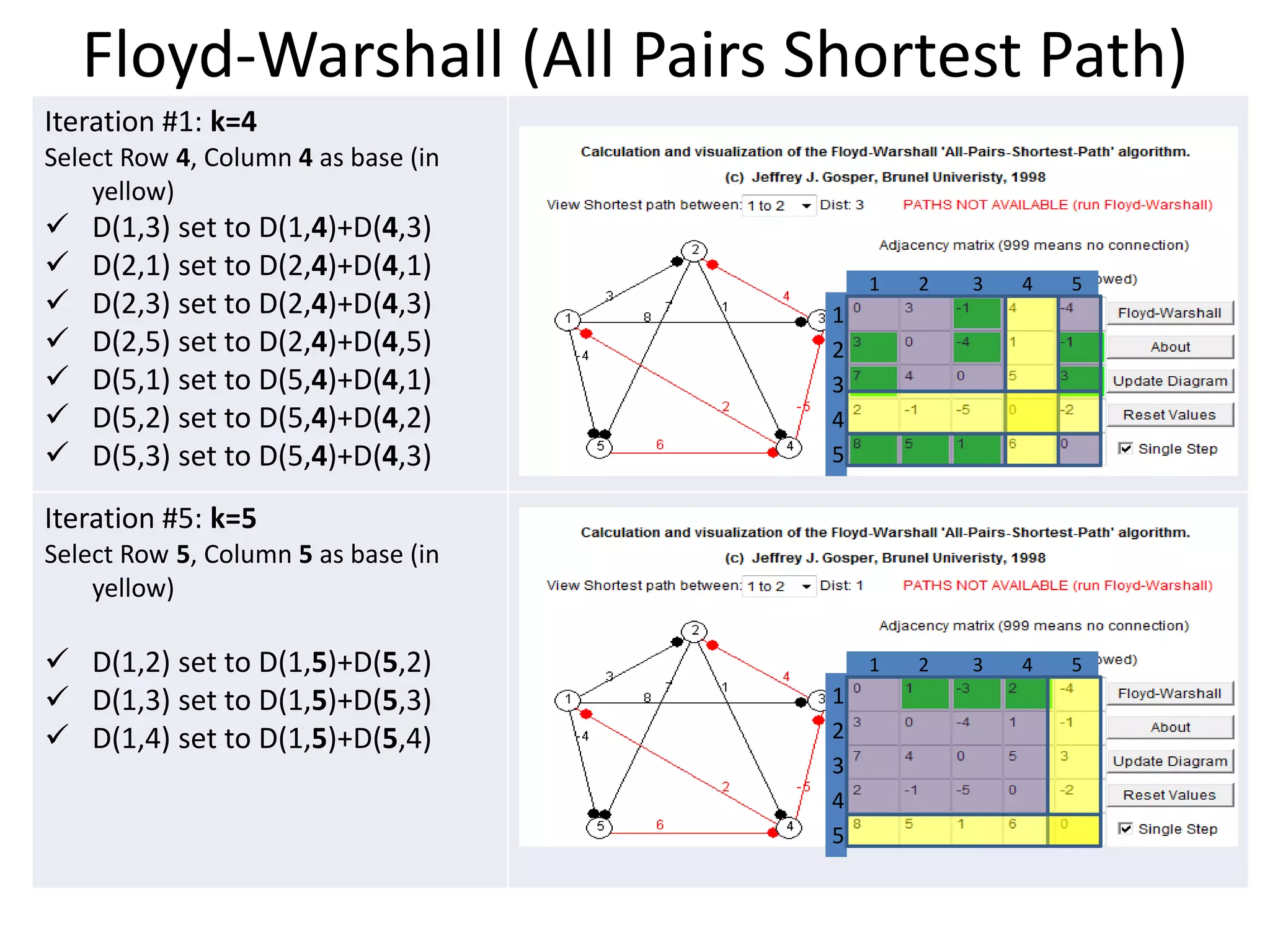
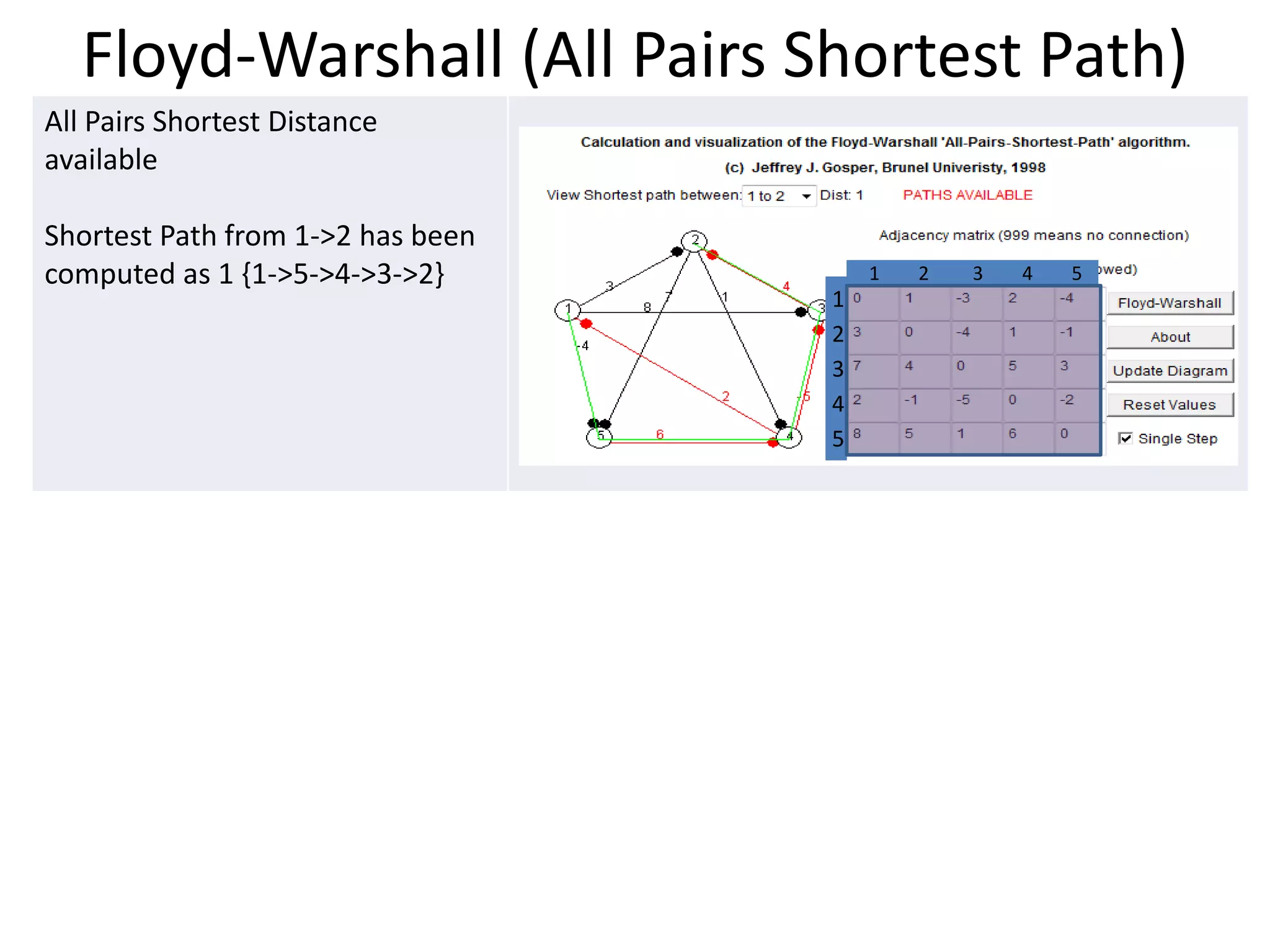
30. Floyd-Warshall (All Pairs Shortest Path)
Initial Graph (Start State)
1. Dots represent arrow direction
2. Red edges are backward flows
3. 999 indicates no direct edge
4. Negative costs included 1 2 3 4 5
1
2
3
4
5
Iteration #1: k=1
Select Row 1, Column 1 as base (in
yellow)
For each cell D(i,j) (in purple) 1 2 3 4 5
Set D(i,j) = min[D(i,j) , D(i,k)+D(k,j)] 1
2
 D(4,2) set to D(4,1)+D(1,2) 3
 D(4,5) set to D(4,1)+D(1,5) 4
5
http://www.pms.ifi.lmu.de/lehre/compgeometry/Gosper/shortest_path/shortest_path.html#visualization

31. Floyd-Warshall (All Pairs Shortest Path)
Iteration #2: k=2
Select Row 2, Column 2 as base (in
yellow)
For each cell D(i,j) (in purple)
1 2 3 4 5
Set D(i,j) = min[D(i,j) , D(i,k)+D(k,j)]
1
2
 D(1,4) set to D(1,2)+D(2,4) 3
 D(3,4) set to D(4,2)+D(2,3) 4
5
Iteration #3: k=3
Select Row 3, Column 3 as base (in
yellow)
For each cell D(i,j) (in purple) 1 2 3 4 5
Set D(i,j) = min[D(i,j) , D(i,k)+D(k,j)] 1
2
 D(4,2) set to D(4,3)+D(3,2) 3
4
5

32. Floyd-Warshall (All Pairs Shortest Path)
Iteration #1: k=4
Select Row 4, Column 4 as base (in
yellow)
 D(1,3) set to D(1,4)+D(4,3)
 D(2,1) set to D(2,4)+D(4,1) 1 2 3 4 5
 D(2,3) set to D(2,4)+D(4,3) 1
 D(2,5) set to D(2,4)+D(4,5) 2
 D(5,1) set to D(5,4)+D(4,1) 3
 D(5,2) set to D(5,4)+D(4,2) 4
 D(5,3) set to D(5,4)+D(4,3) 5
Iteration #5: k=5
Select Row 5, Column 5 as base (in
yellow)
 D(1,2) set to D(1,5)+D(5,2) 1 2 3 4 5
 D(1,3) set to D(1,5)+D(5,3) 1
 D(1,4) set to D(1,5)+D(5,4) 2
3
4
5

33. Floyd-Warshall (All Pairs Shortest Path)
All Pairs Shortest Distance
available
Shortest Path from 1->2 has been
computed as 1 {1->5->4->3->2} 1 2 3 4 5
1
2
3
4
5

34. Maximum Flow
• Given a “Source” (A) and a Capacity in A-> D direction
“Sink” (G), determine the
maximum quantity that can
flow, given edge capacities
• Maximum telephone calls on
a network, maximum
vehicles on a road
• Two-directional flow capacity
Capacity in D->A direction

35. Practical Application of Maximum Flow
• Tyson Foods, IBP Merger in 2001
– Combine Transportation Networks
– Optimize Fleet Carriers (Strategic), Residual Carriers (Contract and Spot
Carriers)
• Approach
– Mine trips data from previous 3 years
– Generate Aggregates (Min, Max, Avg) for each Lane/Start DOW/End DOW
– Run Flow problem iteratively for each start location and start day of week
[Modeled as a single node]
• Result (Cost optimization)
– Propose Routing Loops for Fleet Carriers
– Propose Residual Flow and suggested rates for Contract Negotiations

36. Ford and Fulkerson Method
1. Find any path that has positive „forward‟ flow capacity
remaining
2. Compute f, the flow capacity on the bottleneck edge [This is
the most constricted flow in the chosen path]
3. Add f to the capacity in the forward direction of each edge in
the chosen path. Reduce f from the capacity in the reverse
direction of each edge in the chosen path
4. Repeat 1-3 until positive forward flow paths are found

37. Ford and Fulkerson Method
[Path A->D->E->G]
Flow on Bottleneck Arc [D->E]: 4
Reduce 4 in the forward direction edges
Add 4 in the reverse direction edges
Cumulative flow in the network = 4
[Path A->B->E->G]
Flow on Bottleneck Arc [B->E]: 3
Reduce 3 in the forward direction edges
Add 3 in the reverse direction edges
Cumulative flow in the network = 4+3

38. Ford and Fulkerson Method
[Path A->C->F->G]
Flow on Bottleneck Arc [A->C]: 4
Reduce 4 in the forward direction edges
Add 4 in the reverse direction edges
Cumulative flow in the network = 4+3+4
[Path A->D->F->G]
Flow on Bottleneck Arc [F->G]: 2
Reduce 2 in the forward direction edges
Add 2 in the reverse direction edges
Cumulative flow in the network = 4+3+4+2

39. Ford and Fulkerson Method
[Path A->D->F->E->G]
Flow on Bottleneck Arc [F->E]: 1
Reduce 1 in the forward direction edges
Add 1 in the reverse direction edges
Cumulative flow in the network = 14
(4+3+4+2+1).
There are no more positive flow paths
between A->G. The algorithm terminates.

40. Minimum Cut Problem
•Each ‘cut’ should detach all possible paths
from Source to Sink [A->G]
•‘cut value’ is the sum of flow capacities that
have been severed by the cut
Tit-bit: During Vietnam war, the infamous Ho Chi Minh trail(s) were modeled as
a network and ‘costs’ were associated with cutting the trail at various points.
The min cut then showed the set of trails that must be attacked to sever the flow of enemy
troops and supplies for the lowest cost operation.

41. Multi-stage Transshipment
• Usage of multiple modes – Road, Rail, Air/Sea to deliver
goods
• Intel‟s suppliers in Taiwan provide ICs to be assembled in
its plant in Arizona, USA

42. Multi-stage Transshipment
Rail Hub
Vendor
Plant
Airport Airport
Multi-Leg, Multi-Modal Shipments
Intermodal (Air, Rail, Ship) Schedules drive drayage legs planning
In-transit Optimization - Consolidation, Deconsolidation at transshipment points
Documentation, Import/Export regulations constrain optimization options

43. Minimal Set Covering
• Given
– A universal set U that has all the solutions,
– A number of subsets Si
• Find the smallest number (k) of subsets (Si) that cover all
solutions in U
• Example: Ensure coverage of resources to usage. Find the
smallest number (k) of telephone switches (Subsets Si)
required to cover usage needs of all customers (Universal set
U)
• Intersections can exist

44. Maximum Set Packing
• Given
– A universal set U that has all the solutions,
– A number of subsets Si
• Find the biggest number (k) of disjoint subsets (Si) that cover
all solutions in U.
• Example: Allocate users to resources. Assign maximum
number (k) of airline crews (Subsets Si) to available aircrafts
(Universal set U) such that no crew is assigned to multiple
flights

45. Routing Heuristics and Optimization
• Vehicle Routing Problem – Complicated and comprises of numerous
practical constraints
• Involves Order Consolidation, Mode
Selection, Routing/Transshipments, Scheduling, Location windows and
constraints, Carrier/Lane/Rate choices, Vehicle/Driver assignment, DOT
regulations, Compatibilities, Execution Adaptability
• “heuristics refers to experience-based techniques for problem solving.
Heuristic methods are used to identify an optimal solution as rapidly as
possible. Examples of this method include using a "rule of thumb", an
educated guess, an intuitive judgment, orcommon sense.”
http://en.wikipedia.org/wiki/Approximation_algorithms

46. Consolidation-Centered Heuristic
• Orders from the same origin and to the same destination can be combined to
Bundle one Trip/Shipment. Mode selection is made.
Orders
• Create Multi-Stop trips/shipments by consolidating within mode
[Courier, TruckLoad, LTL, Rail etc]
Consolidate • Assign Best Carrier, Rate
by Mode • Solve Vehicle Assignment problem for Truckload and LTL
• Disband under-utilized trips/shipment and evaluate alternate options to route
them or consolidate with other pre-existing trips
Disband • Assign Best Carrier Rate. Solve Vehicle Assignment problem
Underutilized

47. Vehicle-Centric Routing
• Pick each vehicle at its domicile location and start packing
them up with “similar” groups of orders
Pack orders • Assign Drivers
into vehicles
• Pick Orders that remain unscheduled and schedule them on
existing trucks. If necessary swap out lower-value orders for
higher priority order scheduling
Solve • Arrange Spot Carriers for remaining orders
Remnants • Arrange LTL, Parcel Modes

48. Case Study – Math Modelling
• Problem Statement – A small Warehouse location has the
following constraints
– The location is open 10:00 AM - 5:00 PM Mon
– It can accommodate only 2 Trucks every hour
– It can only serve 2000 KG of material each hour
• Given:
– 10 Trips picking up goods from the warehouse, each with different
potential start times and corresponding costs. Each trip carriers 500
KG
• Objective:
– Date/Time Schedule the 10 trips with the lowest overall cost such
that all location constraints are honored

49. Objective Function
• Minimize total cost of solution
Minimize obj:
1000 x1 + 1234 x2 + 1343 x3 ….+ 2123 x10 + ….
[Cost of unique Trip and Start Time combination]
[All variables are made linear: 0 ≤ xi ≤ 1. Fractional results are converted to its
closest integer{0,1}. This makes the problem easier to solve. This is called Linear
Programming (LP) Relaxation.]
• Add Above (50,000 - Soft) and Below (3,000 - Soft) Target
Penalty variables
3000 x221 + 50000 x222 + 3000 x223 + 50000 x224 +……
* Integer programs are complicated to solve. Linear programs can be solved in polynomial time

50. Trip Constraints
• A trip can only start at one of its possible start times
Subject To
C1: x1 + x21 + x33 + x112 = 1 [x1, x21, x33 and x112 represent 4
different times trip can pickup at the location]
C2: x2 + x22 + x34 + x 113 = 1
…
…

51. Capacity Constraints
• Location can server two trips in each hour bucket
• Location can serve trips totaling 2000 KG in each hour
bucket
C101: x2 + x26 + x32 + x64 + x76 =2
[Each constraint corresponds to a specific 1-hour bucket. Each of the variables correspond to a trip at a particular pickup time
that falls in that one hour bucket. If that trip is selected, it contributes a trip count of 1 to the Bucket Capacity of 2 trips]
C102: 500x1 + 500x13 + 500x55 + 500x84 + 500x96 =2000
[Each constraint corresponds to a specific 1-hour bucket. Each of the variables correspond to a trip at a particular pickup time
that falls in that one hour bucket. If that trip is selected, it contributes 500 KG to the Bucket Capacity of 2000 KGS]
…
…
* Concept of Slack variables to accommodate lesser quantity than capacity

52. Balancing Constraints
• To create a balanced workload and prevent peaks. Helps
ramp-up and ramp-down labor resources
C201: x187 – x188 – x189 + x190 >=0
[The difference between adjacent time bucket assignments should be kept low].
Creates a pattern such as this ….
2.5
2
1.5
1 Series1
0.5
0
9 10 11 12 1 2 3 4 5