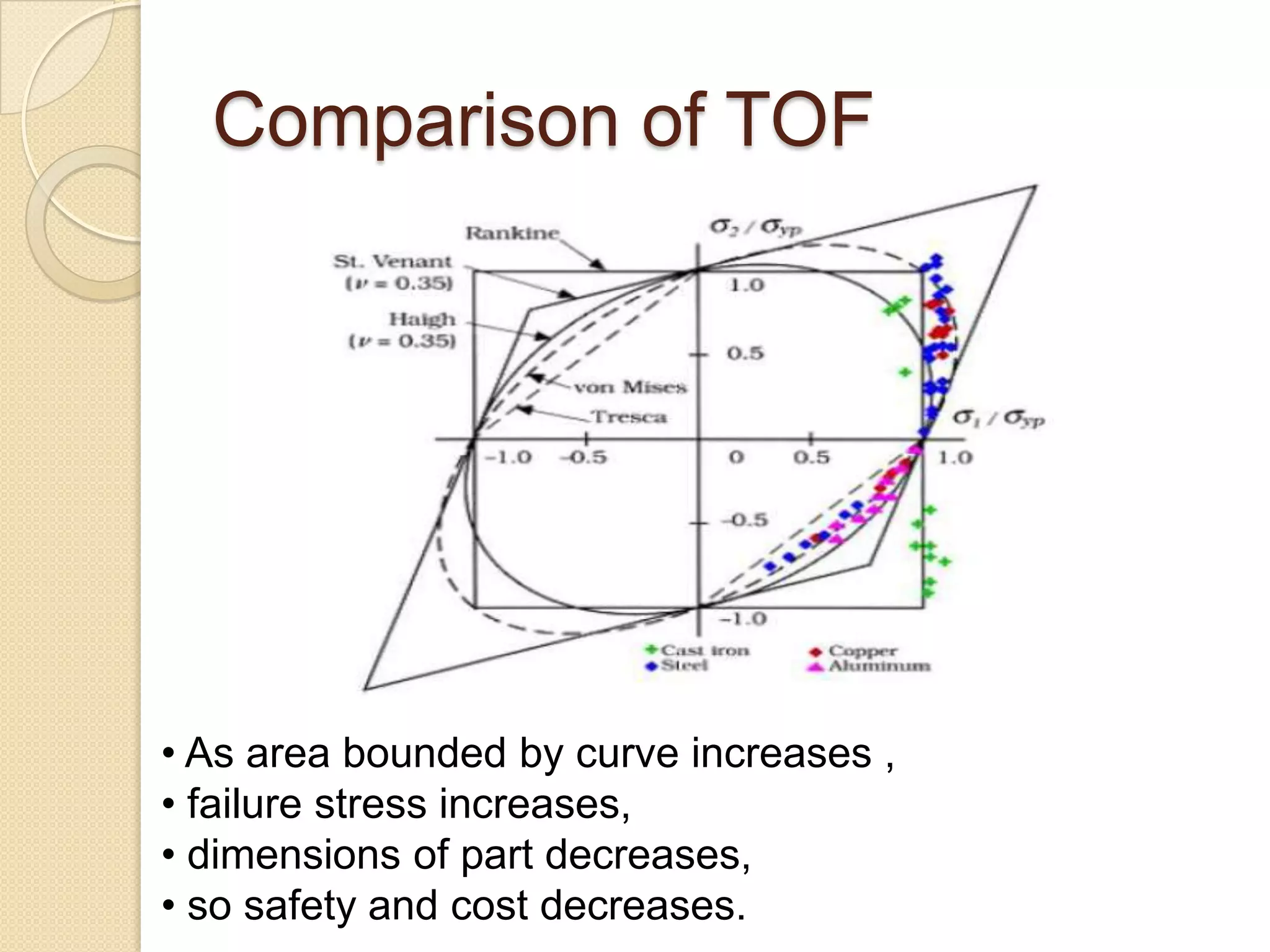
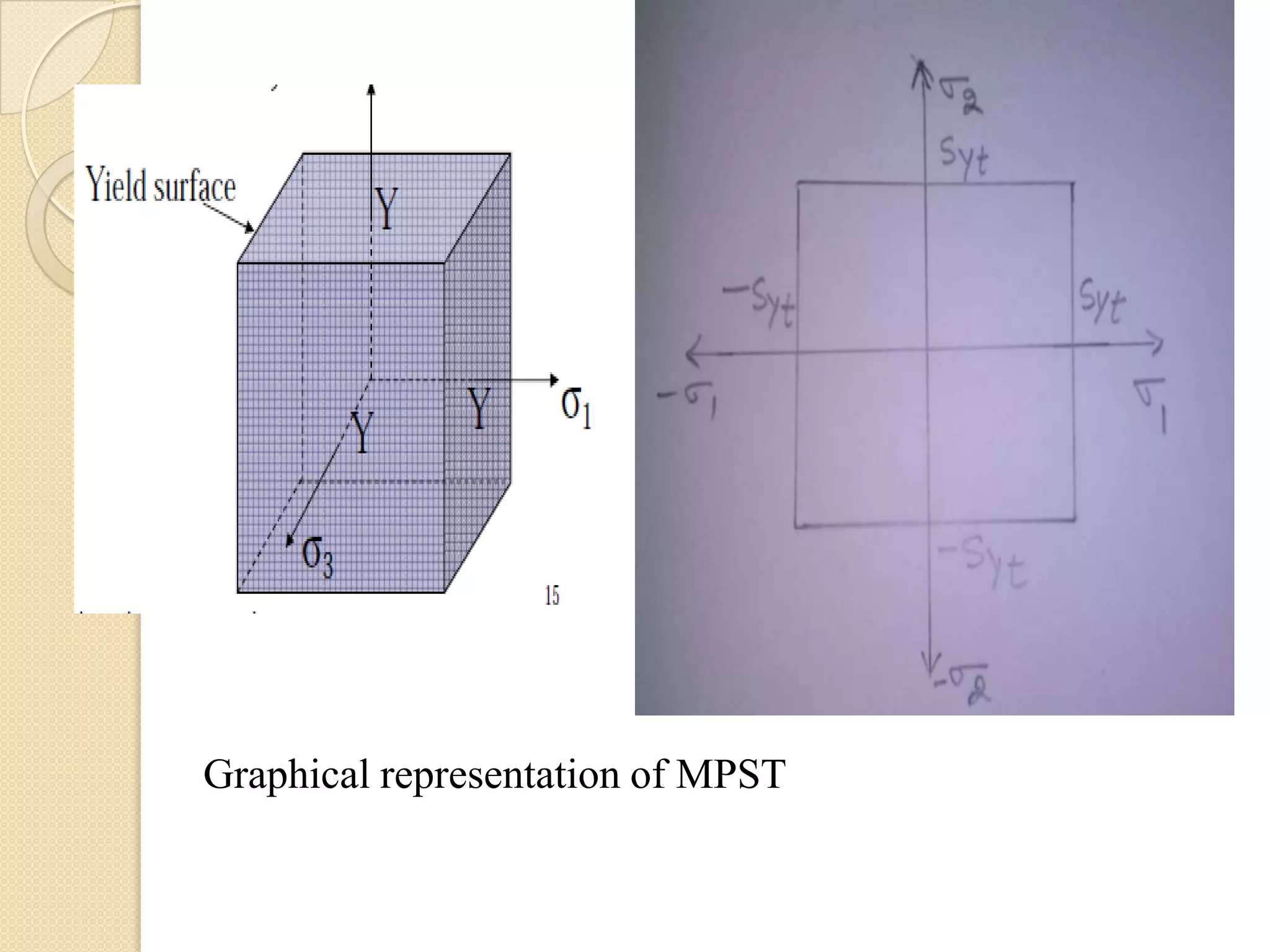
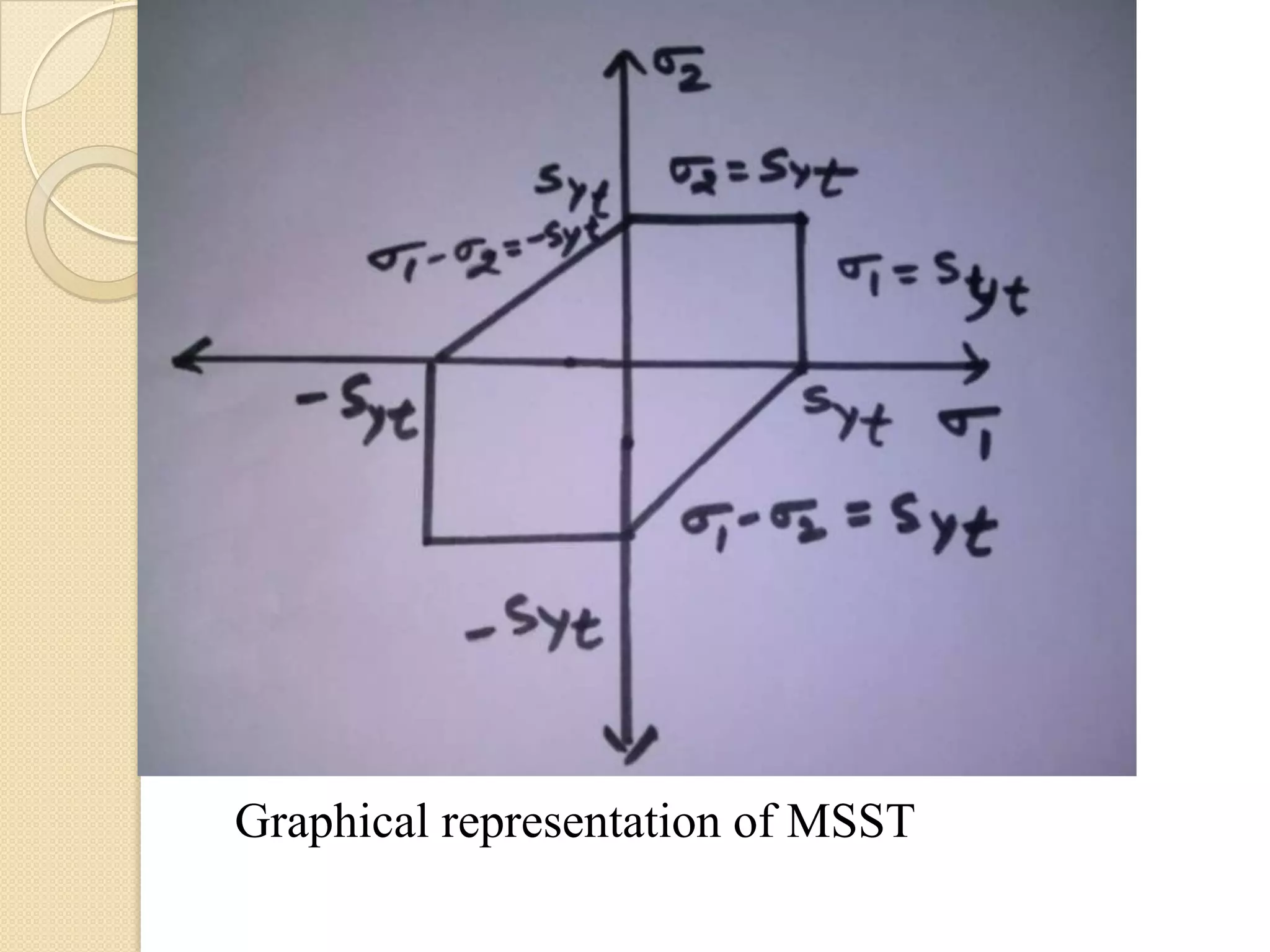
The document discusses various theories of failure that are used to determine the safe dimensions of components under combined loading conditions. It describes five theories: (1) Maximum principal stress theory, (2) Maximum principal strain theory, (3) Maximum strain energy theory, (4) Maximum distortion energy theory, and (5) Maximum shear stress theory. The maximum distortion energy theory provides the safest design for ductile materials as it results in the largest allowable stresses before failure compared to the other theories. The document also compares the various theories and discusses when each is best applied depending on the material type and stress conditions.

1. Mechanical Behavior of
Materials
Topic: Theories of Failure
Submitted To: Submitted
By:
Dr. Sanjeev Kumar Mandeep
Kumar
Prof. in MED SID: 13209024

2. Requirement of TOF
 Theories of failure are used to determine
the safe dimension of a component
when it is subjected to combined
stresses due to various loads.
 Theories of failure are used in design by
establishing a relationship between
stresses induced under combined
loading conditions and properties
obtained from tension test like Syt & Sut

3. Various Theory Of Failure
• Maximum principal stress theory (Rankine’s
Theory)
• Maximum principal strain theory (St.
Venant’s theory)
• Maximum strain energy theory (Haigh’
Theory)
• Maximum Distortion energy theory (Von-
mises and Henky’s Theory)
• Maximum shear stress theory (Guest and
Treska’s Theory)

4. Maximum Principle Stress
Theory:
 Condition For Failure:
σ1 > Syt or Sut
 Condition for safe design:
σ1 < Syt/N or Sut/N
Where N is factor of safety.
 For ductile material:
Syc > Syt > Sys
 For Brittle material:
Syc > Sys > Syt
cont.

5. Maximum Principle Stress
Theory
 This theory is suitable for the safe design of
machine component made up of brittle
material, because brittle material are weak in
tension
 This theory is not good for design of ductile
material because shear failure may occur
 But this theory is also suitable for ductile
material under following condition :
1. uniaxial state of stress condition.
2. Under biaxial state of stress when are like in
nature.
3. Hydrostatic stress condition.

6. Graphical representation of MPST

7. Maximum shear stress theory
 Condition For Failure:
 Condition for safe design:

8. For triaxial state of stress
condiition
For biaxial state of stress: σ3=0
When σ1 & σ2 are like in nature:
σ1 < Sty/N
When σ1 & σ2 are unlike :
σ1- σ2 < Syt/N

9. Graphical representation of MSST

10.  MPST and MSST will give same
result under biaxial state of stress
when principle stresses are like in
nature.
 M.S.S.T. is not valid under hydrostatic
stress condition (because every plane
passing through the point is principle
plane hence absolute shear stress is
zero)
 M.S.S.T. Gives over safe design for
ductile material .(safe and

11. Maximum principal strain theory:
 Condition For Failure:
 Condition for safe design:

12. For Biaxial state of stress: σ3 = 0
So

13. Maximum strain energy theory:
 Condition For Failure:
Total strain energy/vol > [(S.E/vol)yp]TT
 Condition for safe design:
Total strain energy/vol < [(S.E/vol)yp]TT
Under triaxial loading condition:

14. By putting the values in safe design condition, we get:
For Biaxial state of stress, σ3=0
• It is a equation of ellipse whose graphical
representation is shown in figure.

15. • For hydrostatic stresses, it is the best theory.

16. Maximum Distortion energy theory:
 Condition For Failure:
Max. D.E. / volume > [(D.E./vol.)yp]TT
 Condition for safe design:
Max. D.E. / volume < [(D.E./vol.)yp]TT
 Max. D.E. / vol = Total S.E. /vol – volumetric S.E. / vol

17. By inserting the values of energies in D.E.equation
We got:
By inserting the values of energies in Safe design condition
We got:

18. For biaxial state of stress:
This is a equation of ellipse with
Semi major axis = 1.414 Syt
Semi minor axis = 0.816 Syt

19. Comparison of TOF
• As area bounded by curve increases ,
• failure stress increases,
• dimensions of part decreases,
• so safety and cost decreases.

20.  Area of MDETcurve > area of MSST curve
 So dimension of MDET < dimension of
MSST
 MPST, MSST, MDET will give same result
under biaxial state of stress of same
nature i.e. σ1=σ2= σ and σ3=0

21. Conclusion:
 MPST:
 Best TOF for brittle material design.
 Suitable for ductile material under three
case.
 MSST:
 Gives safe design for ductile.
 MDET:
 Best TOF for ductile material design.

22. Thank You