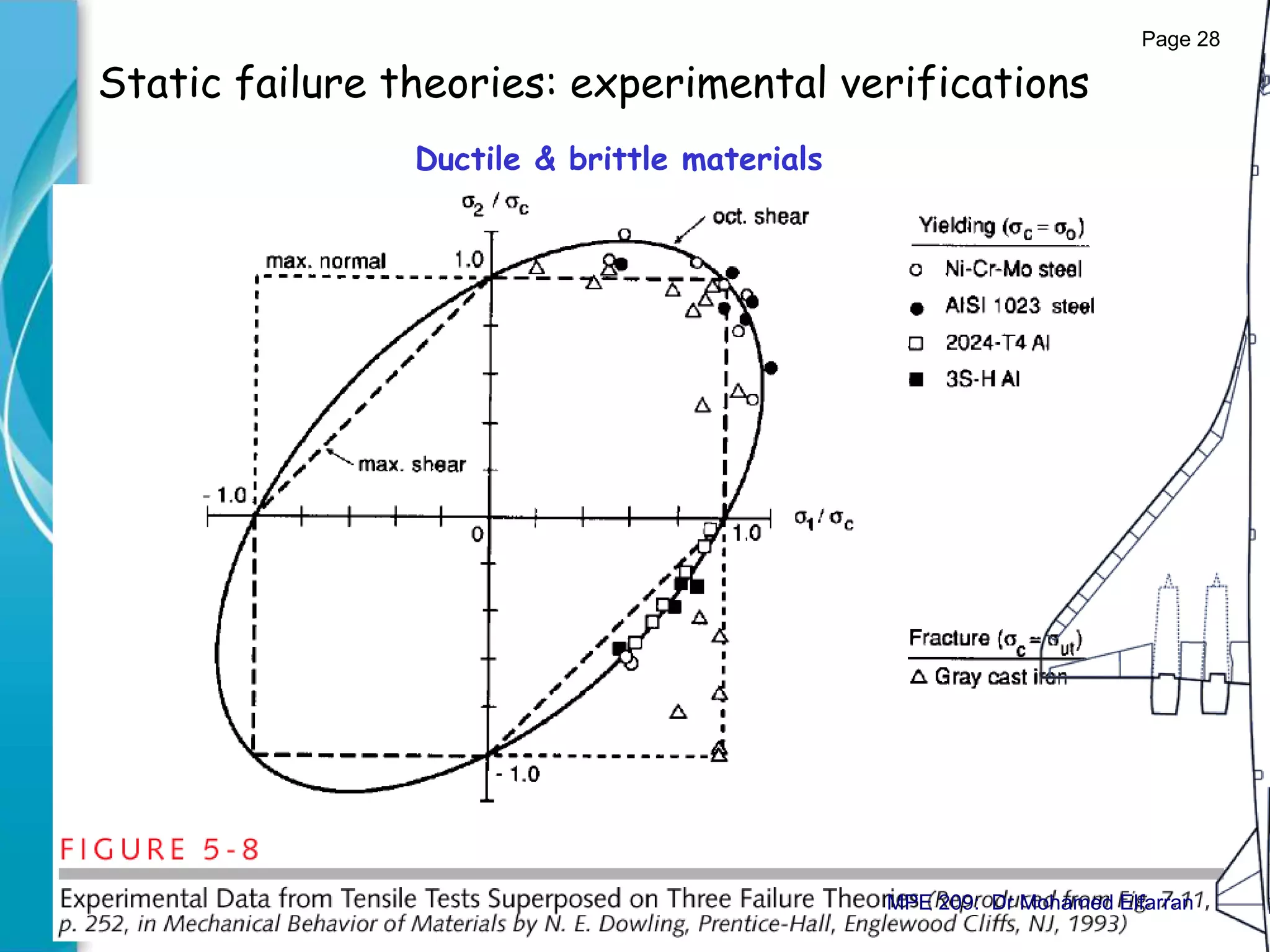
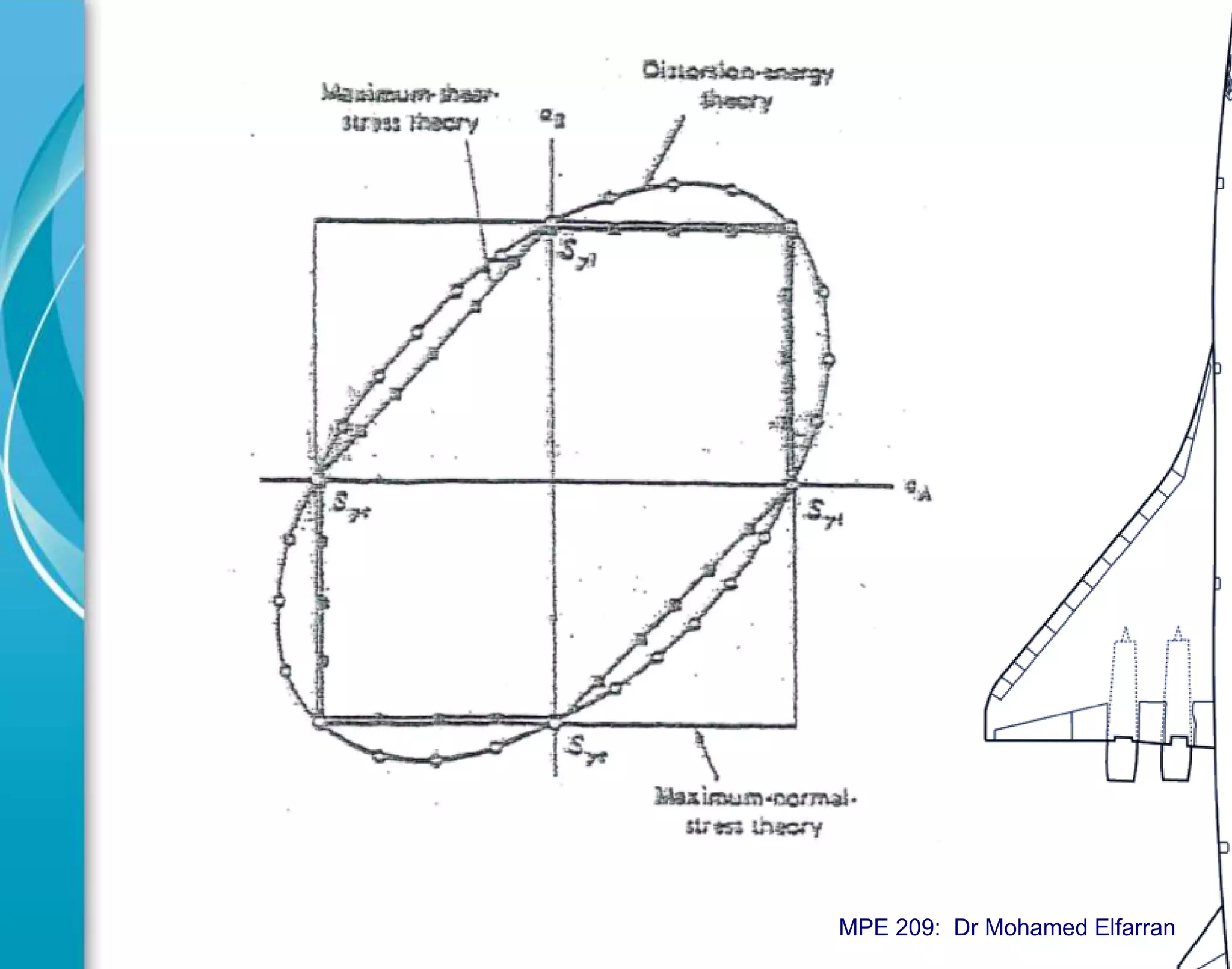
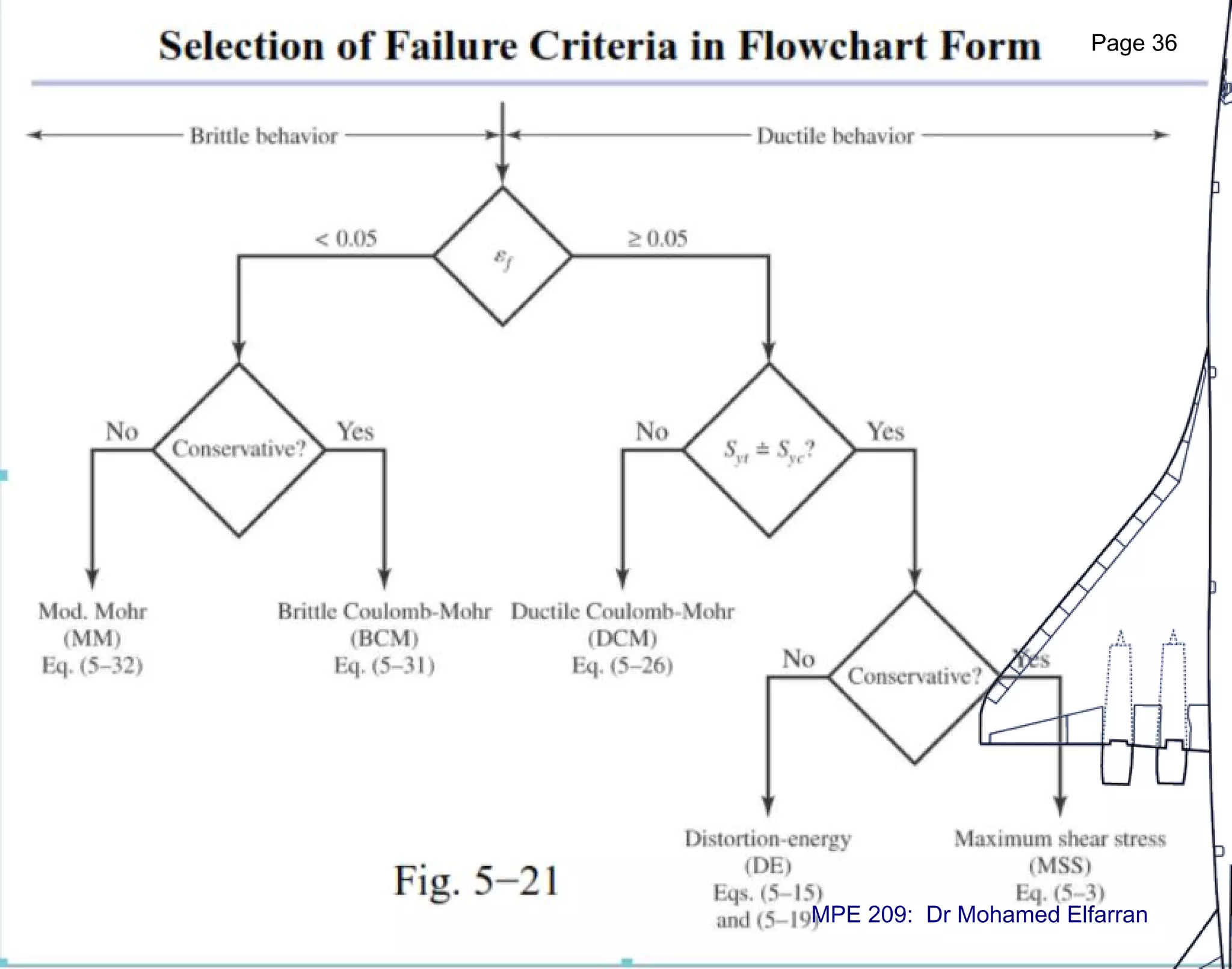
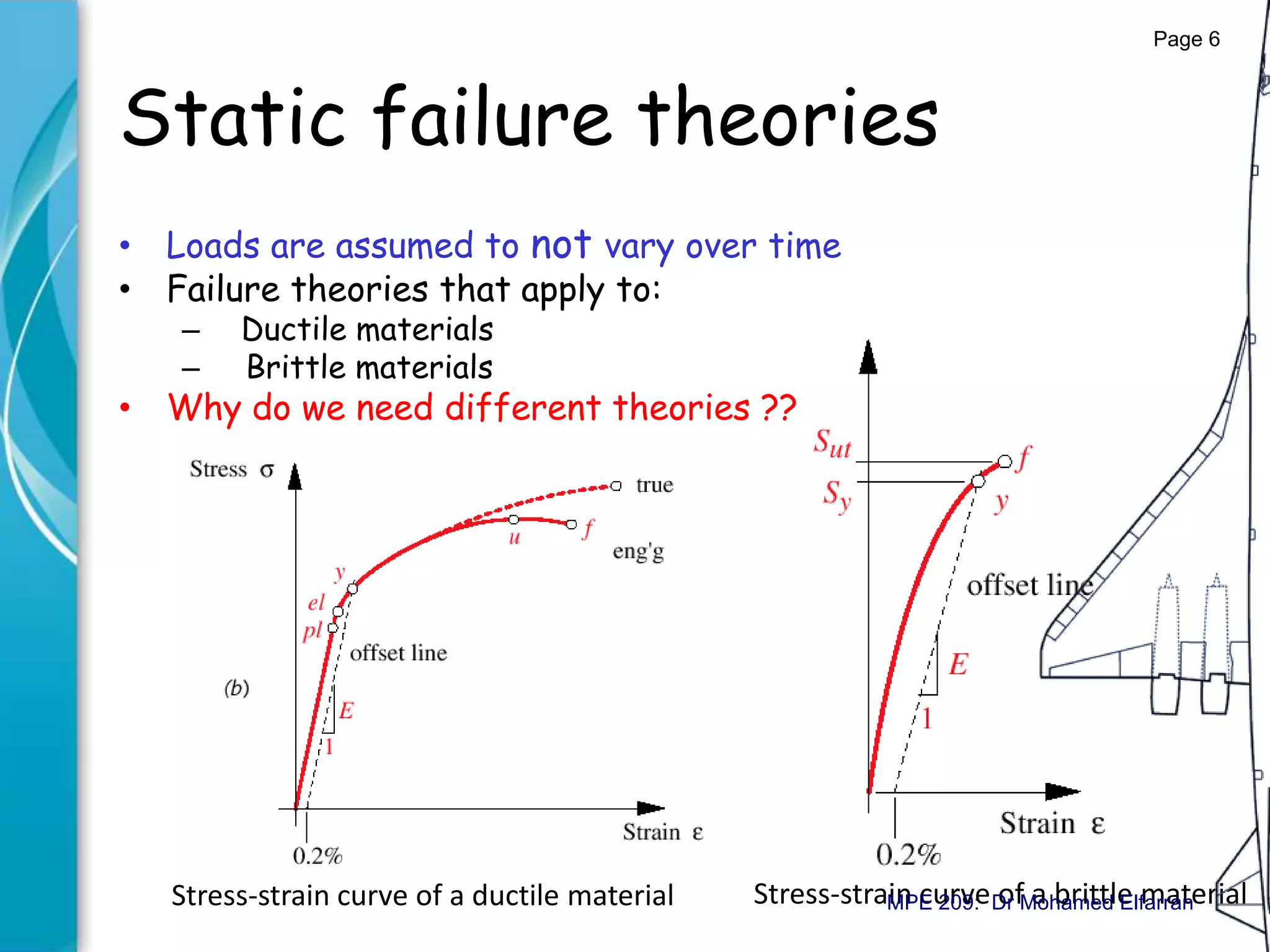
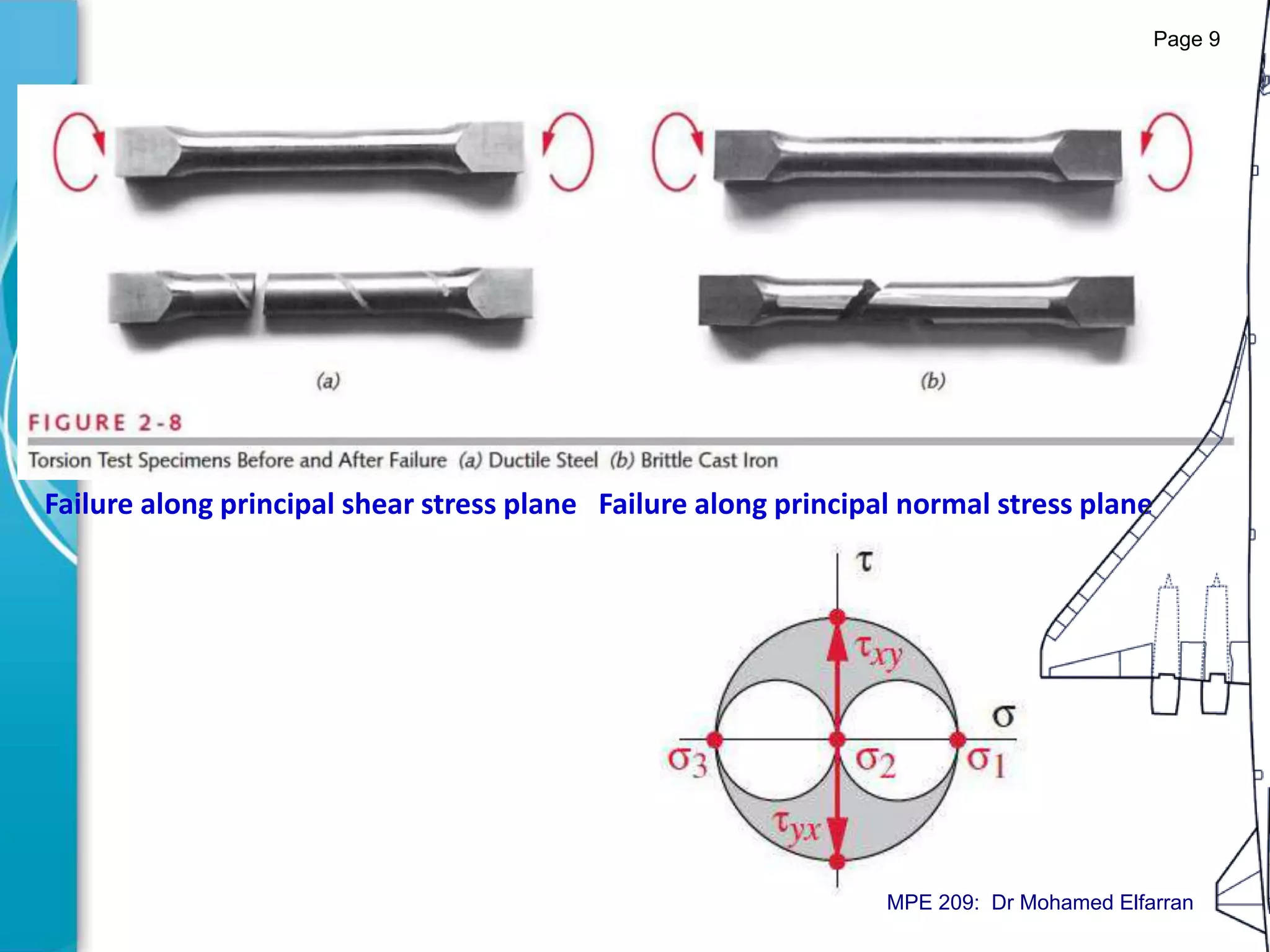
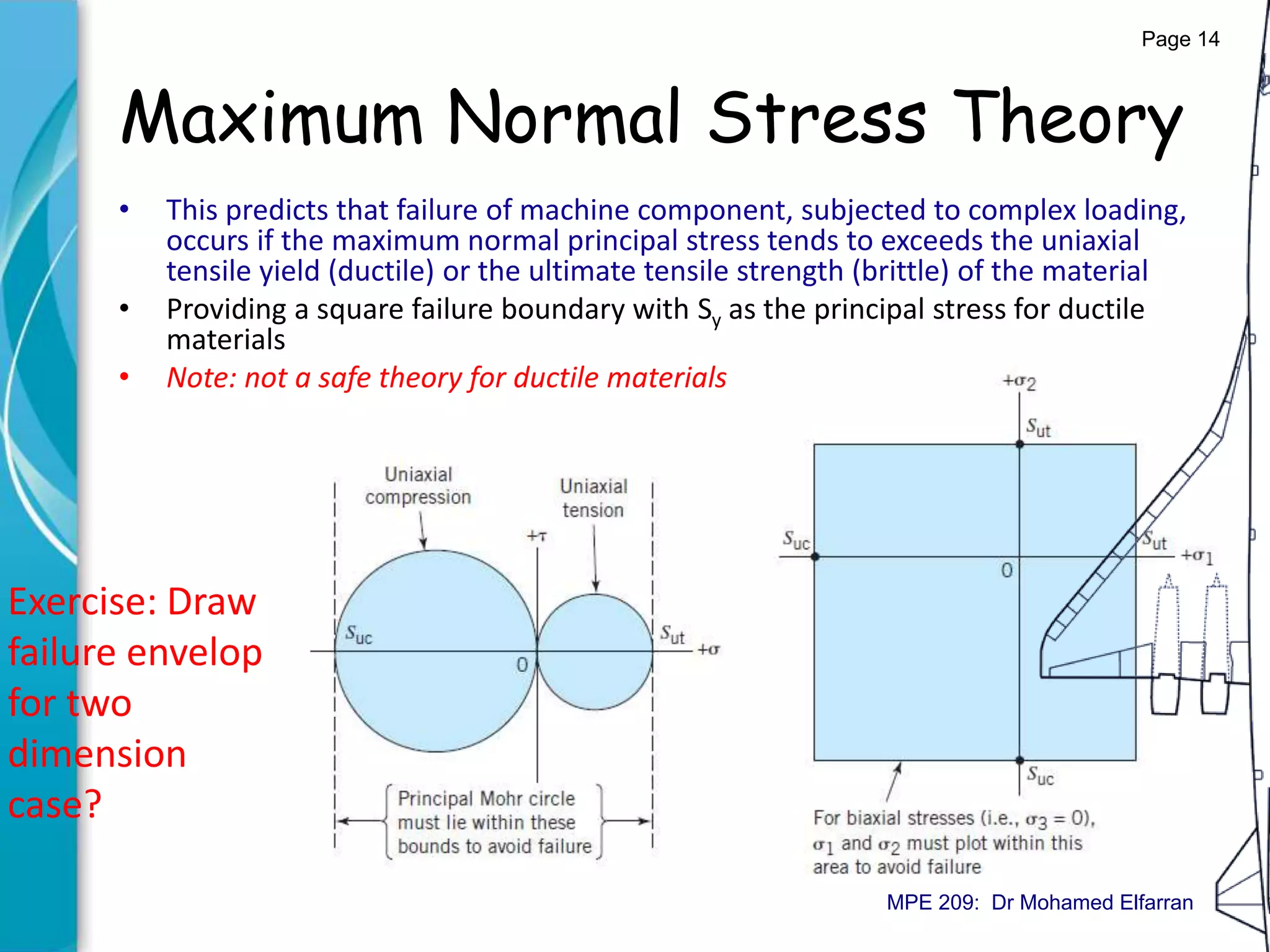
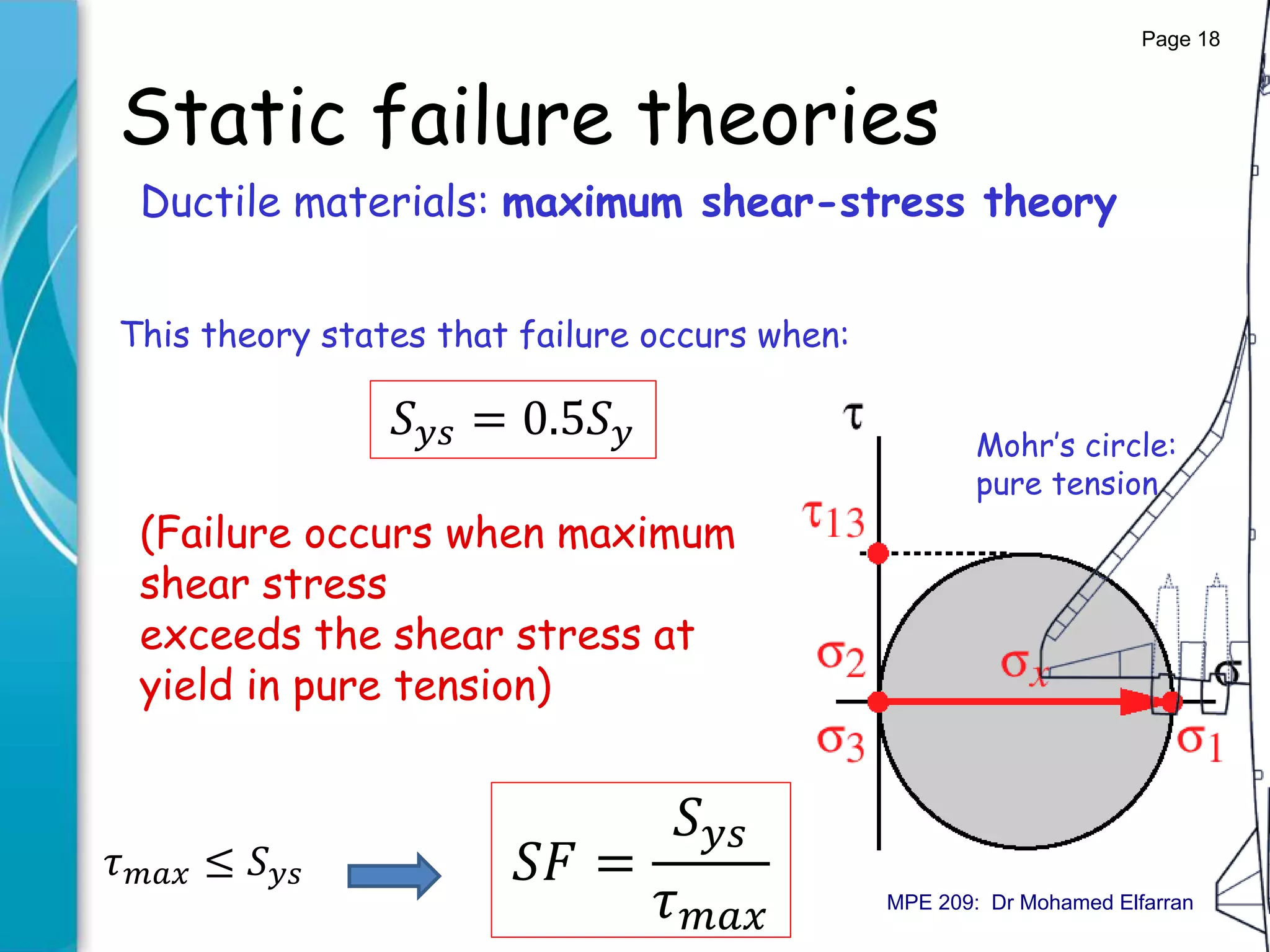
The document discusses static failure theories in engineering, explaining why machine parts fail due to stress exceeding material strength. It differentiates between elastic and fracture failures and outlines various failure theories applicable to ductile and brittle materials. Key concepts include the importance of shear and tensile strengths, and how different loading conditions affect failure mechanisms.














![Static failure theories
Ductile materials: total strain energy
Using previous expressions, total energy is:
𝑈 =
1
2
𝜎𝜀 =
1
2𝐸
[𝜎1
2
+ 𝜎2
2
+ 𝜎3
2
− 2𝜐(𝜎1 𝜎2 + 𝜎2 𝜎3 + 𝜎3 𝜎1)
which can be expressed as 𝑈 = 𝑈ℎ + 𝑈 𝑑
Hydrostatic energy Deformation energy
𝑈ℎ =
3
2
(1 − 2𝜐)
𝐸
𝜎ℎ
2
𝜎ℎ =
𝜎1 + 𝜎2 + 𝜎3
3
Obtained by setting:
𝑈ℎ = 𝑈(𝜎1 = 𝜎2 = 𝜎3 = 𝜎ℎ)
𝑈 𝑑 =
1 + 𝜐
3𝐸
[𝜎1
2 + 𝜎2
2 + 𝜎3
2
−(𝜎1 𝜎2 + 𝜎2 𝜎3 + 𝜎3 𝜎1)]
Obtained by setting:
𝑈 𝑑 = 𝑈 − 𝑈ℎ
Page 21
MPE 209: Dr Mohamed Elfarran](https://image.slidesharecdn.com/mpe209lec41-201116171650/75/MEP-209-Design-of-Machine-elements-LEC-4-21-2048.jpg)

![Static failure theories
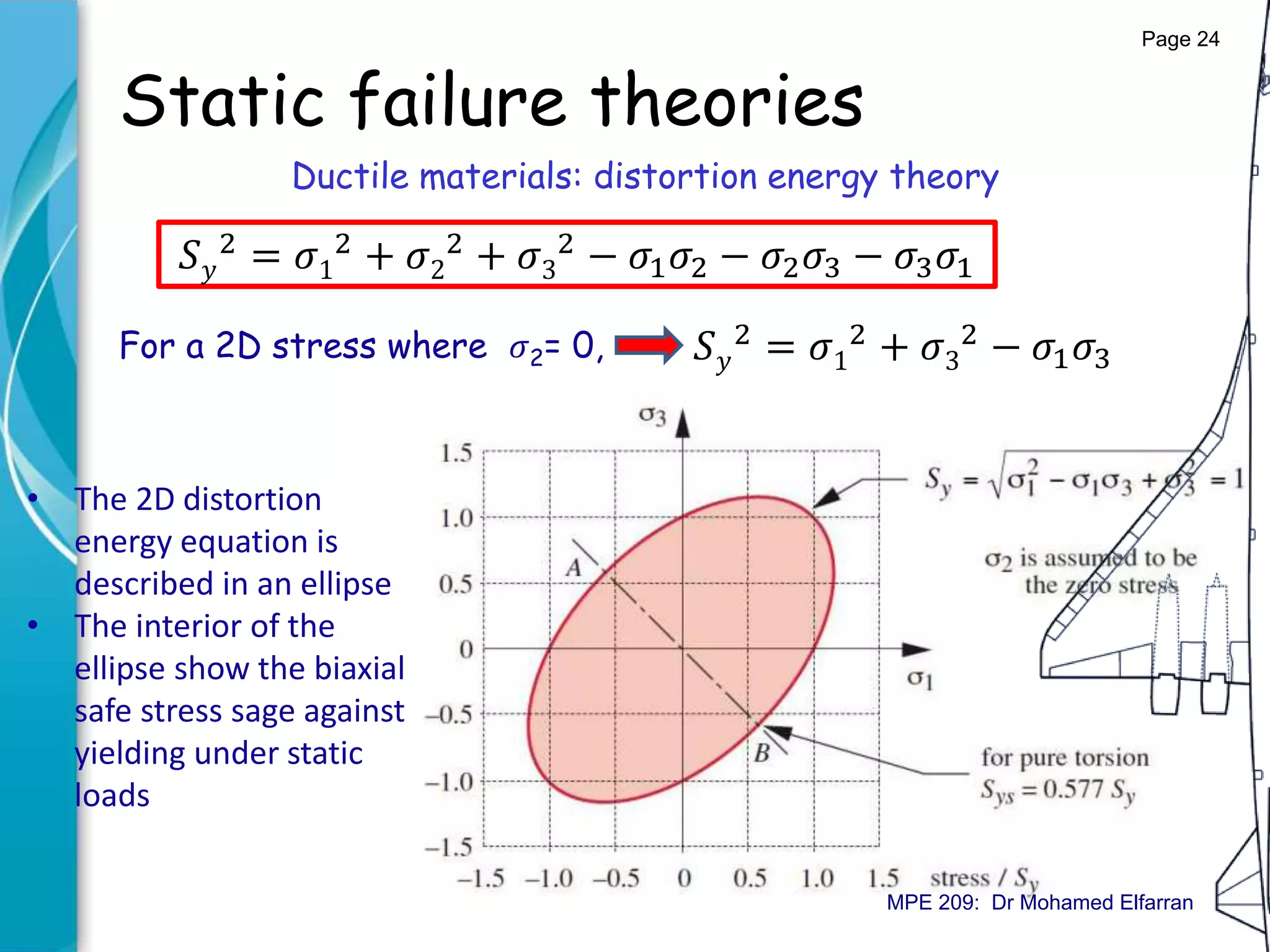
Ductile materials: distortion energy theory
𝑈 𝑑 =
1 + 𝜐
3𝐸
[𝜎1
2 + 𝜎2
2 + 𝜎3
2 − 𝜎1 𝜎2 + 𝜎2 𝜎3 + 𝜎3 𝜎1 ]
For any other state of stresses:
Failure criterion is obtained by setting:
1 + 𝜐
3𝐸
[𝜎1
2
+ 𝜎2
2
+ 𝜎3
2
− (𝜎1 𝜎2 + 𝜎2 𝜎3 + 𝜎3 𝜎1] ≤
1 + 𝜐
3𝐸
𝑆 𝑦
2
Distortion energy:
uniaxial stress at
yield
Distortion energy:
any other state of
stresses
𝜎1
2 + 𝜎2
2 + 𝜎3
2 − 𝜎1 𝜎2 − 𝜎2 𝜎3 − 𝜎3 𝜎1 ≤ 𝑆 𝑦
2
Page 23
MPE 209: Dr Mohamed Elfarran](https://image.slidesharecdn.com/mpe209lec41-201116171650/75/MEP-209-Design-of-Machine-elements-LEC-4-23-2048.jpg)
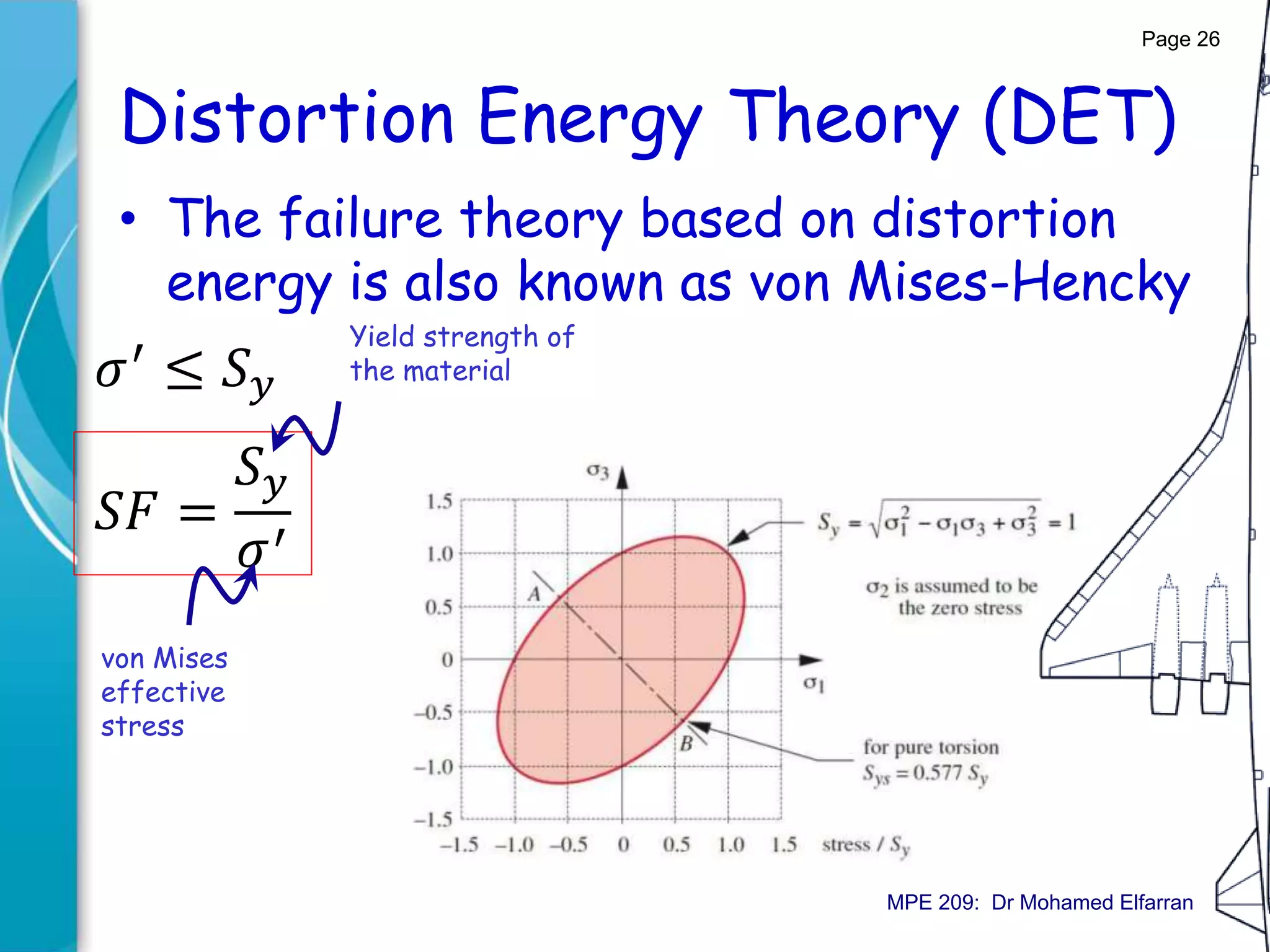
![Static failure theories
Ductile materials: distortion energy theory
Von Mises effective stress
𝑆 𝑦
2 = [𝜎1
2 + 𝜎2
2 + 𝜎3
2 − 𝜎1 𝜎2 − 𝜎2 𝜎3 − 𝜎3 𝜎1] ≡ 𝜎′ 2
Definition:
𝜎′ = 𝜎1
2
+ 𝜎2
2
+ 𝜎3
2
− 𝜎1 𝜎2 − 𝜎2 𝜎3 − 𝜎3 𝜎1
(Yield surface)
von Mises effective stress
von Mises effective stress: uniaxial stress that would create the
same distortion energy as is created by actual combination of
applied stresses
Page 25
MPE 209: Dr Mohamed Elfarran](https://image.slidesharecdn.com/mpe209lec41-201116171650/75/MEP-209-Design-of-Machine-elements-LEC-4-25-2048.jpg)