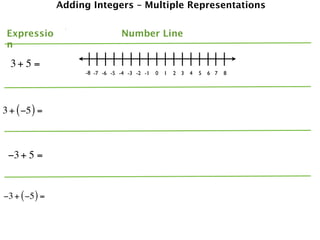
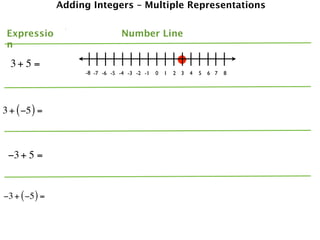
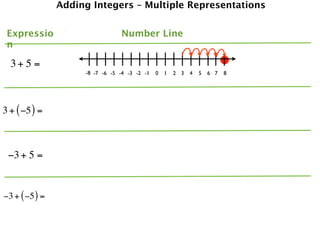
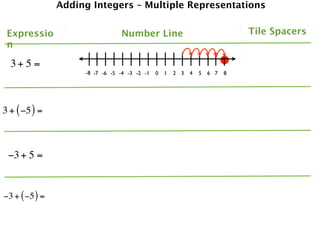
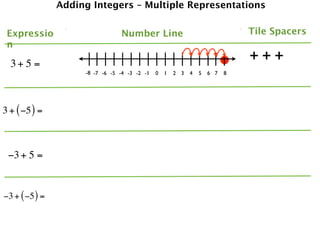
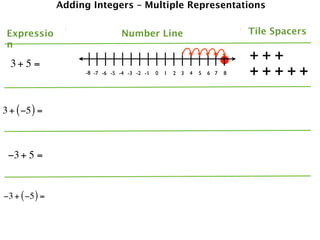
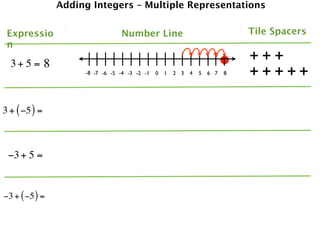
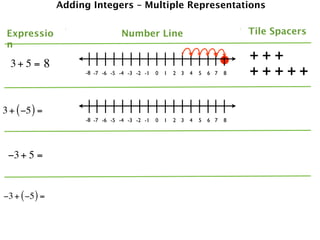
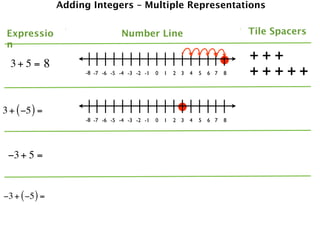
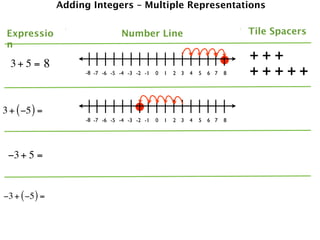
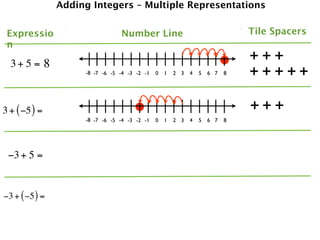
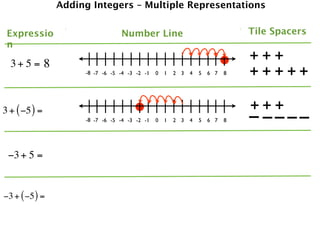
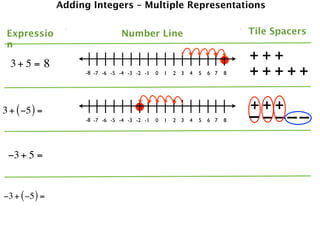
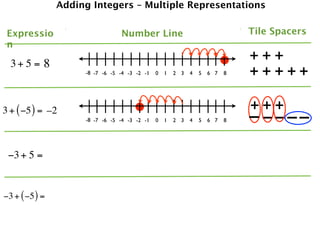
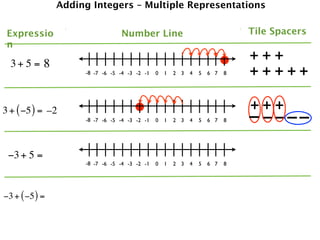
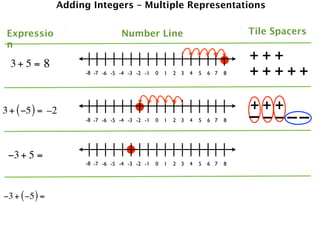
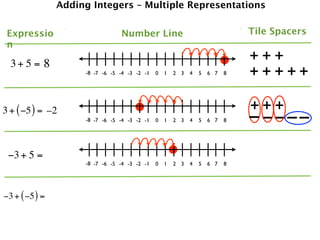
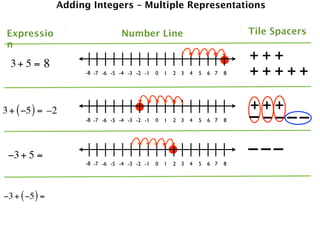
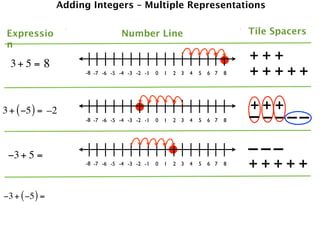
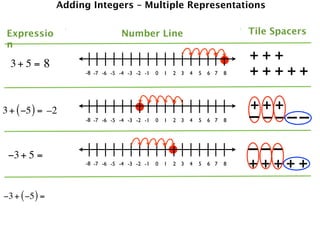
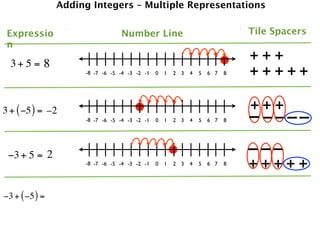
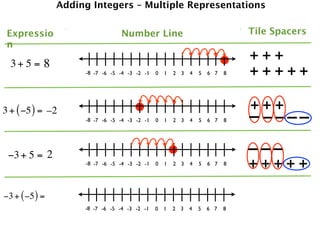
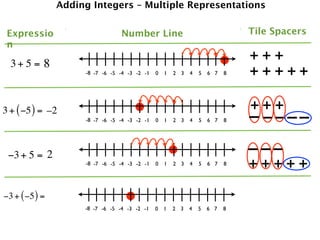
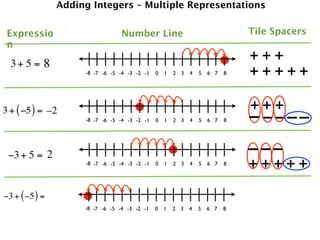
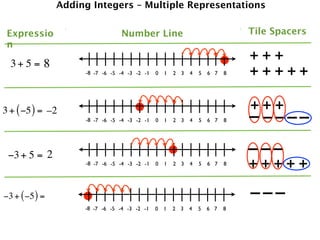
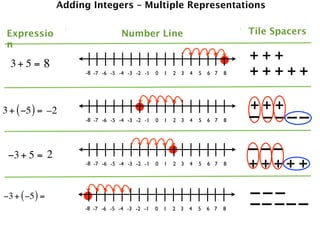
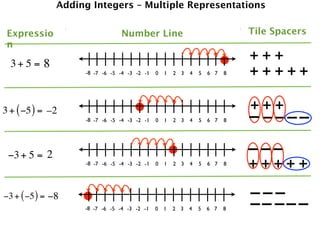
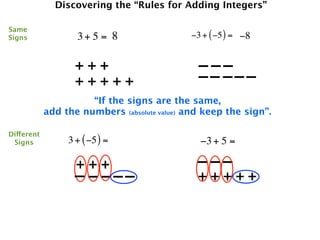
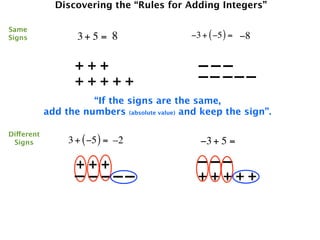
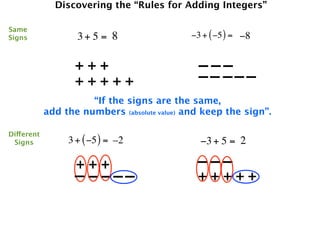
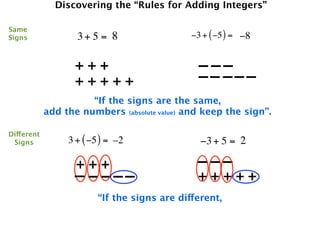
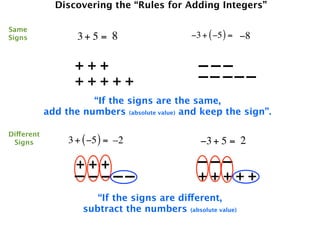
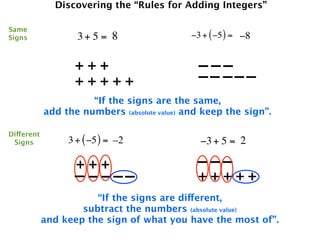
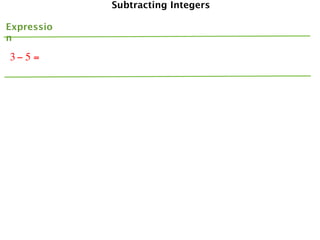
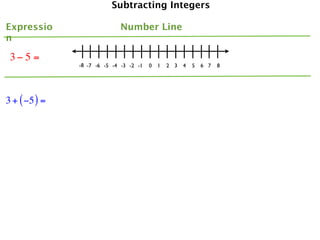
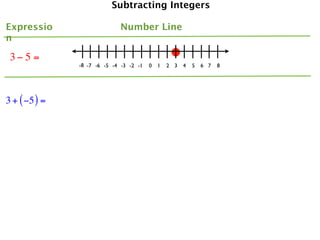
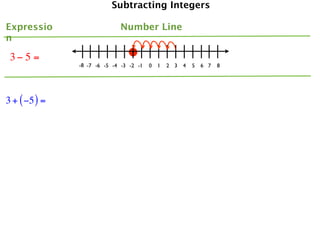
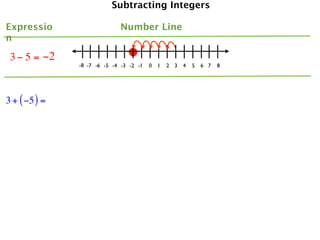
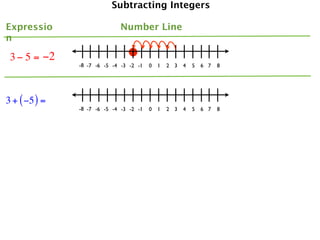
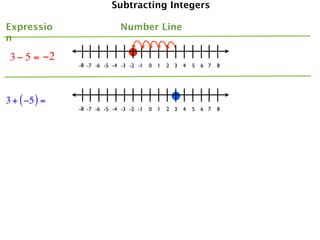
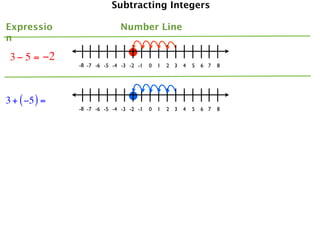
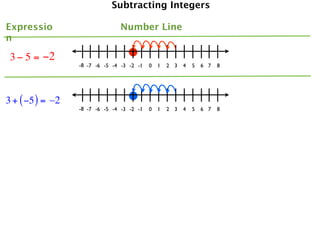
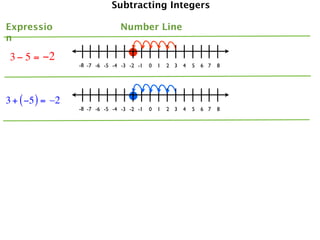
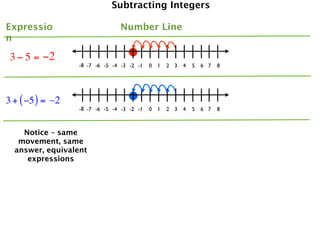
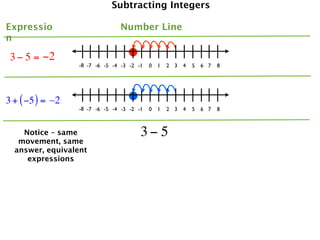
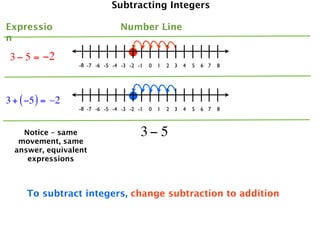
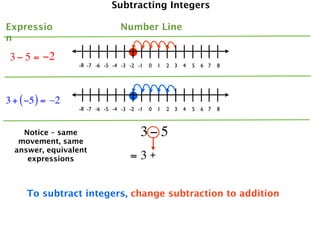
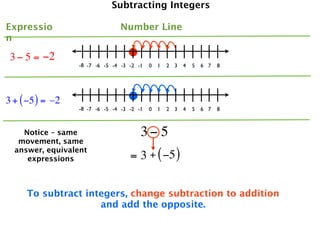
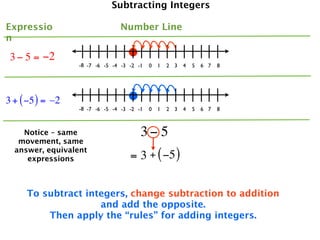
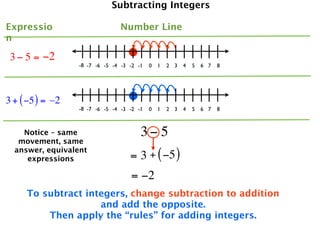
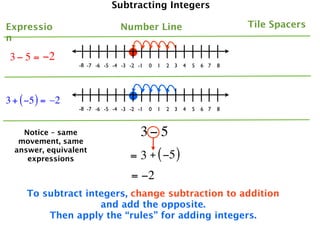
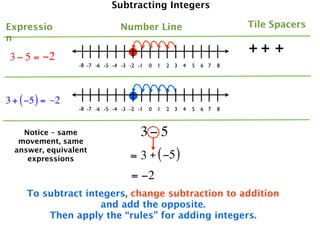
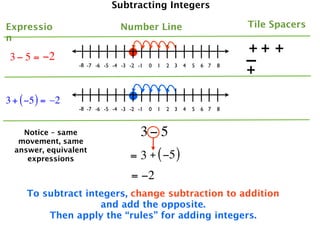
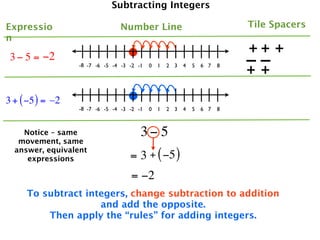
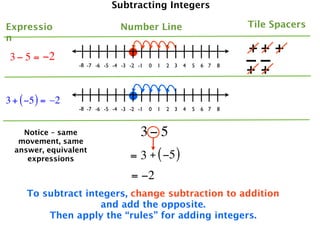
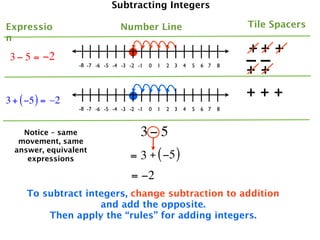
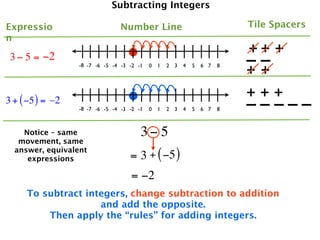
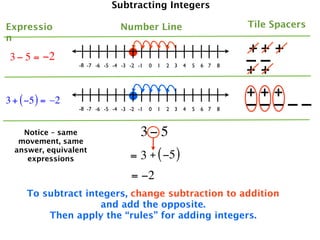
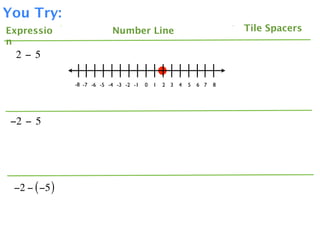
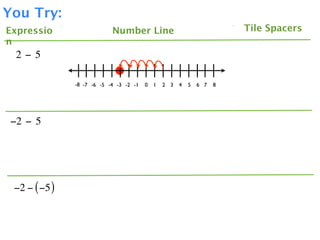
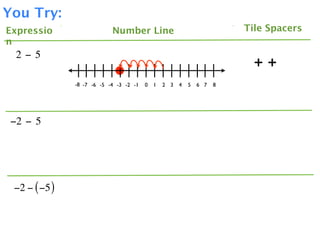
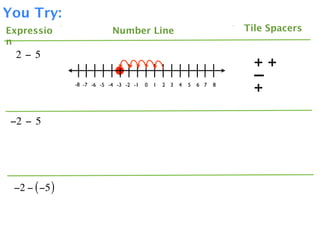
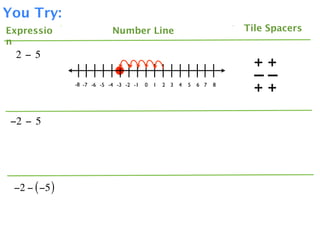
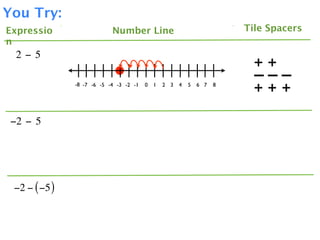
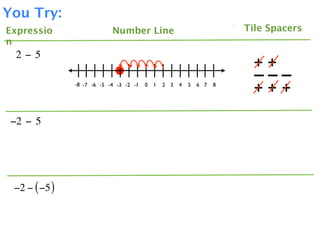
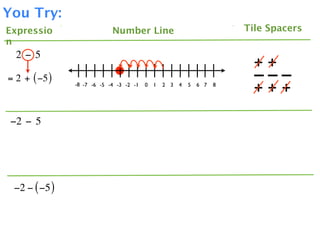
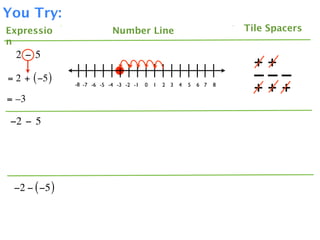
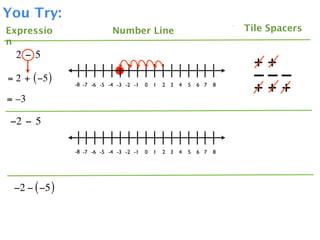
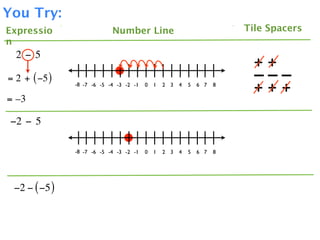
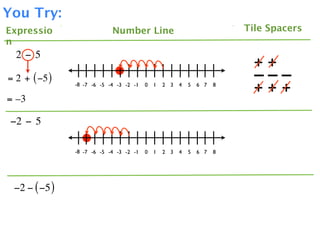
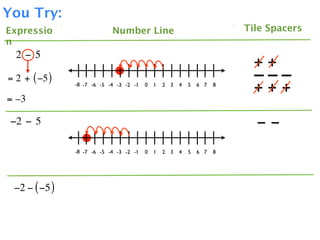
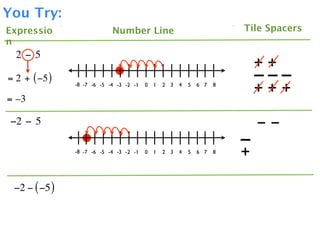
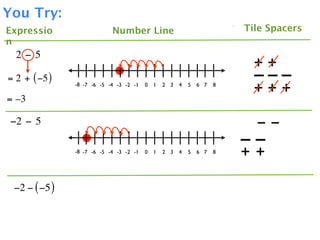
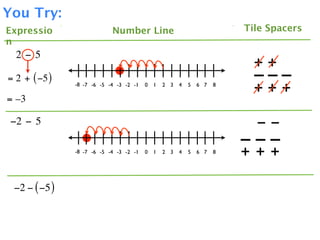
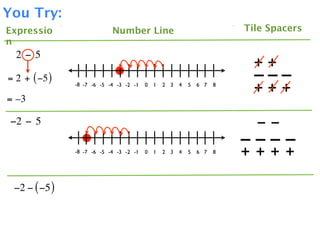
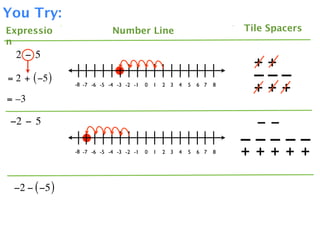
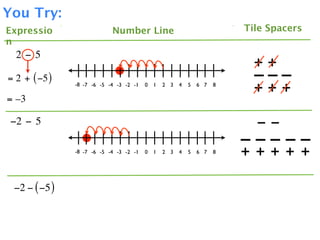
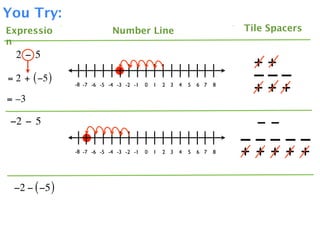
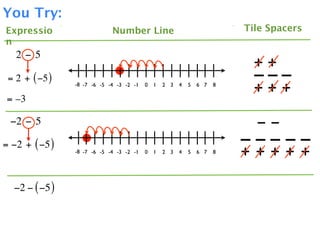
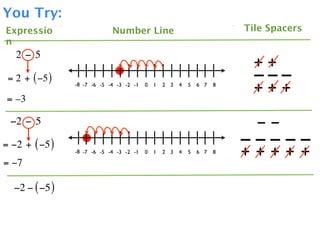
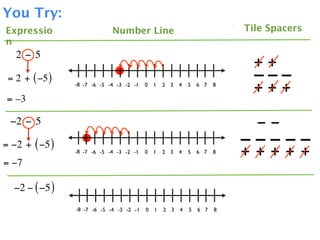
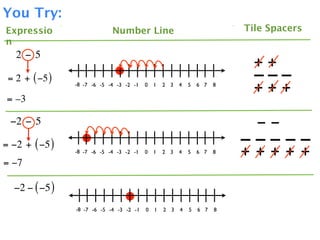
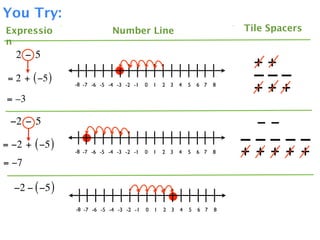
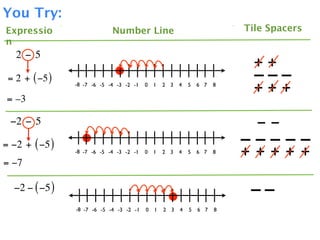
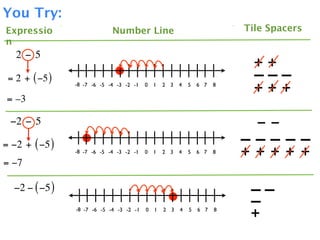
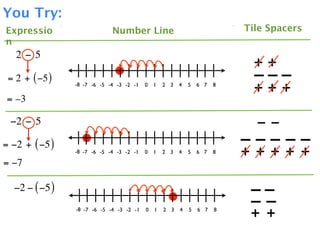
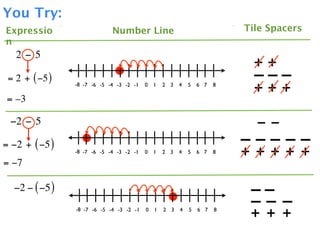
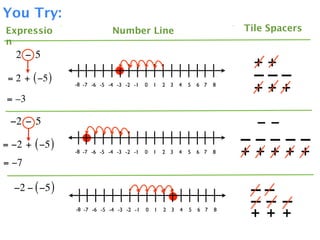
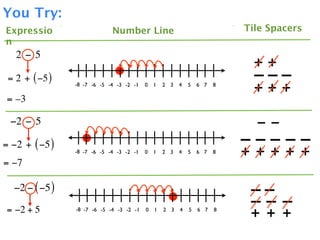
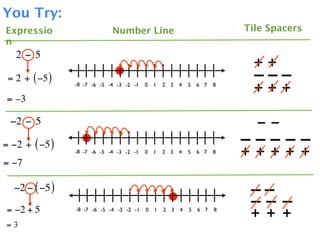
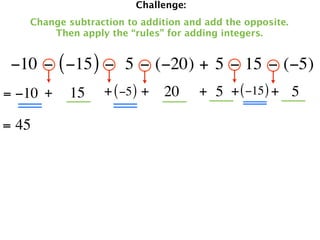
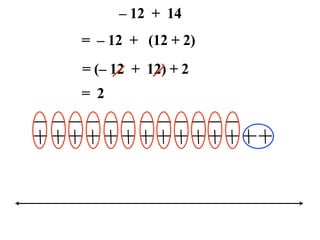
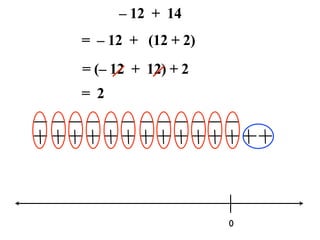
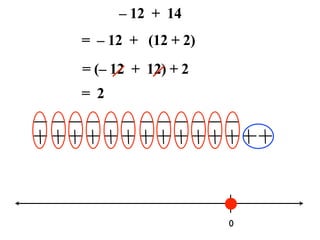
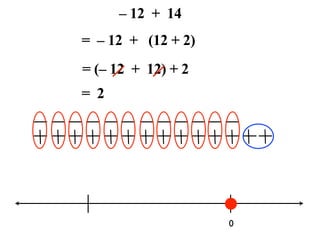
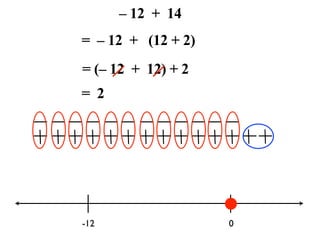
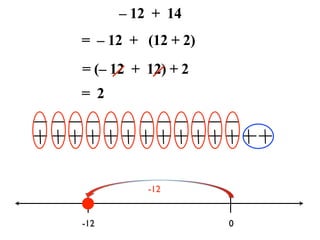
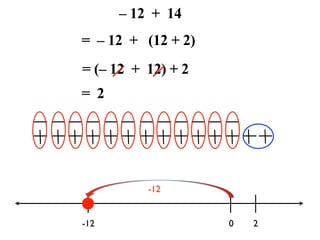
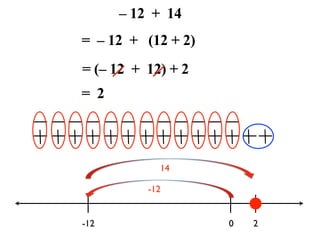
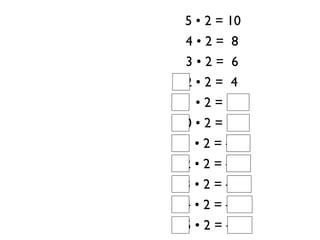
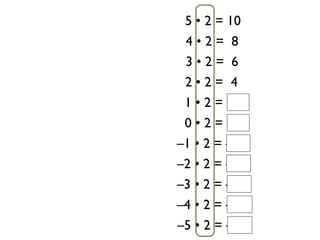
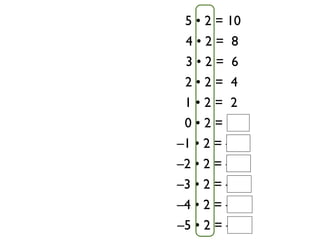
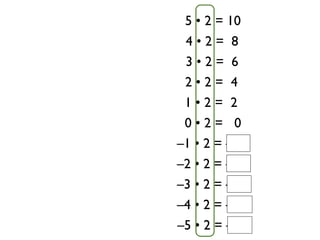
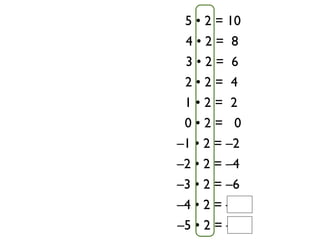
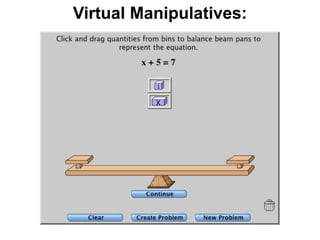
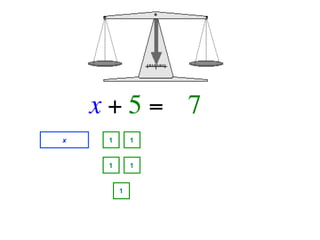
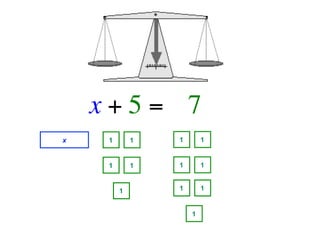
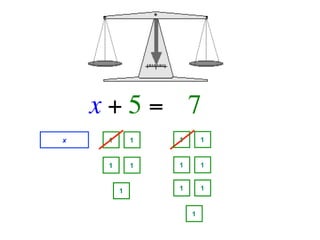
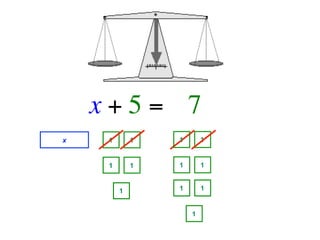
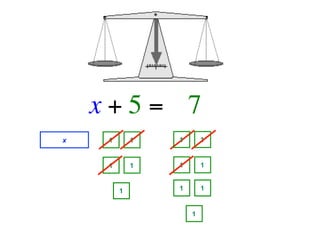
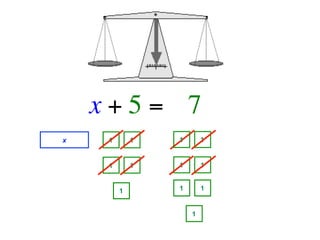
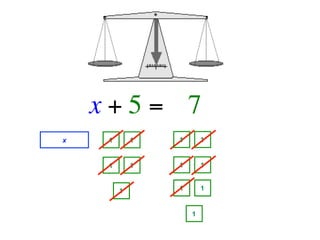
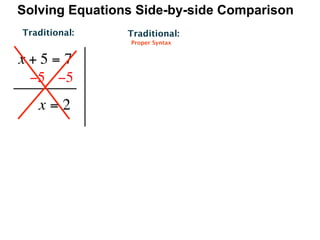
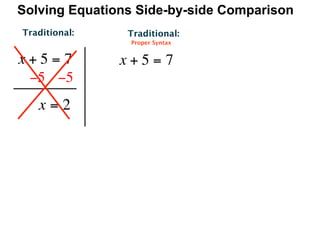
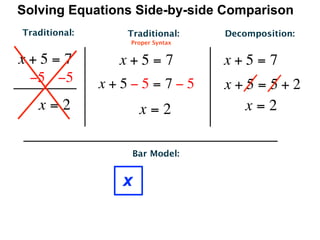
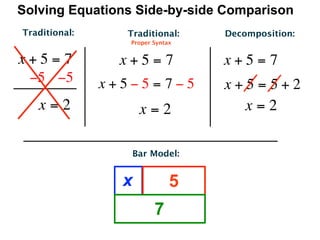
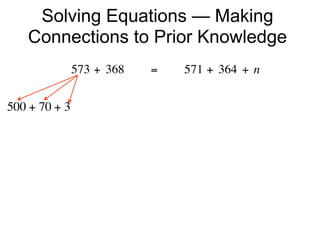
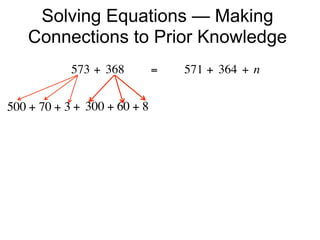
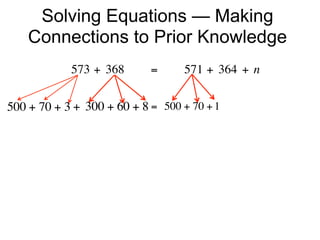
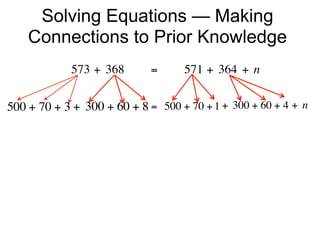
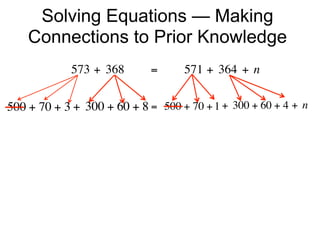
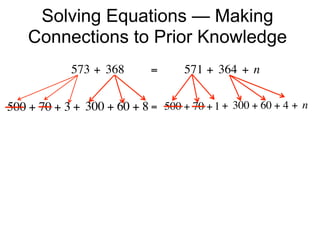
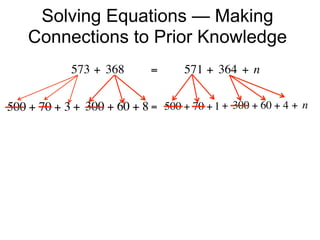
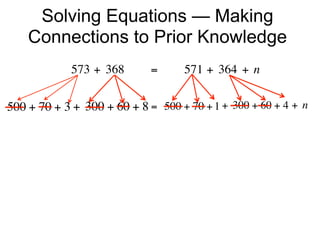
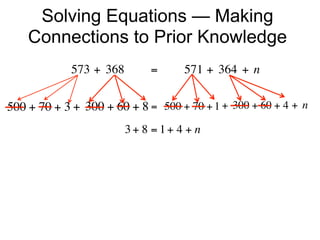
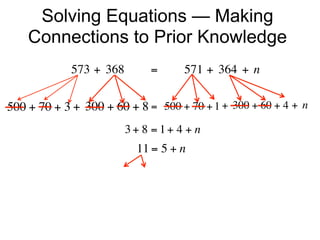
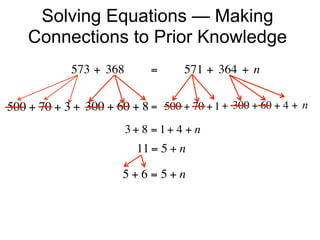
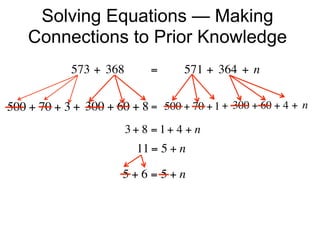
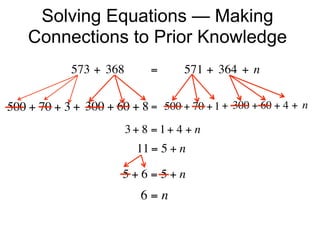
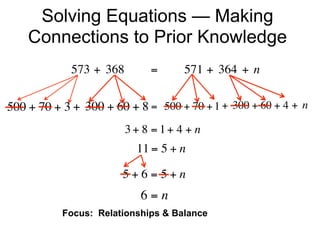
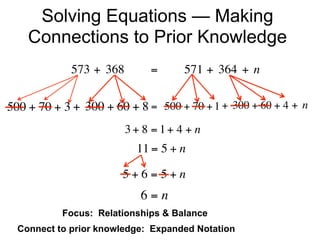
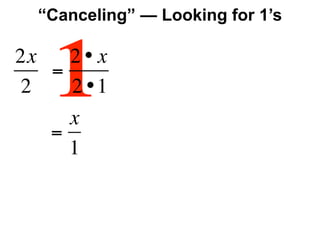
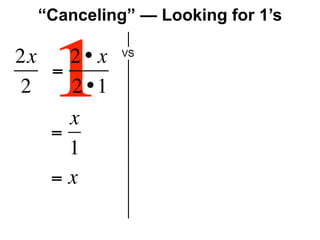
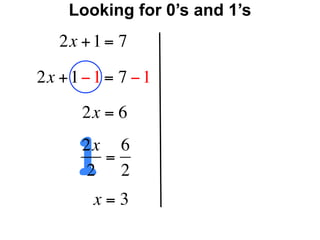
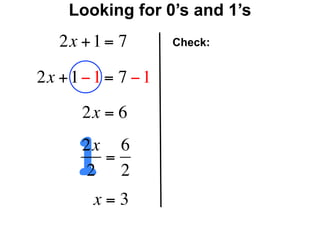
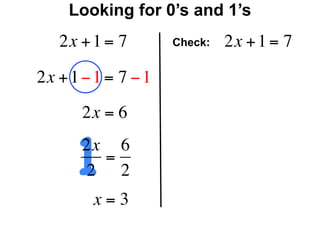
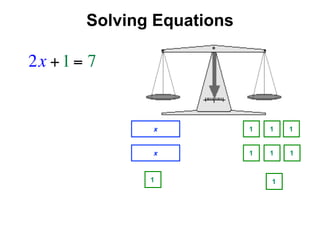
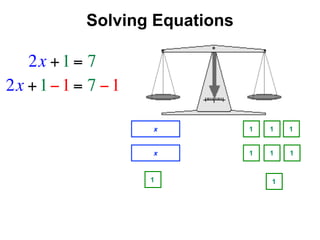
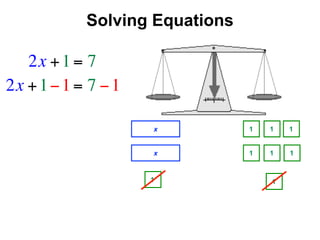
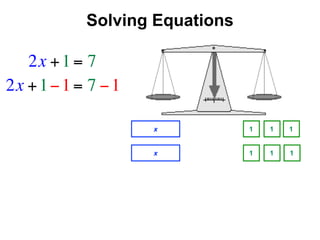
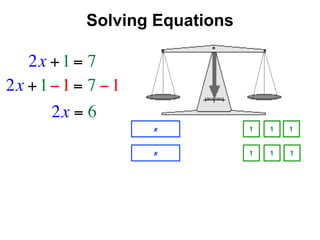
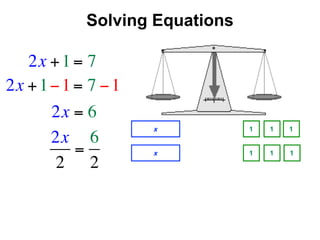
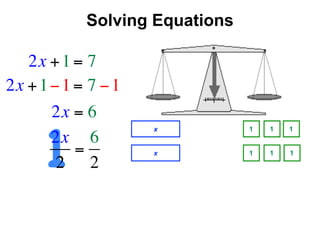
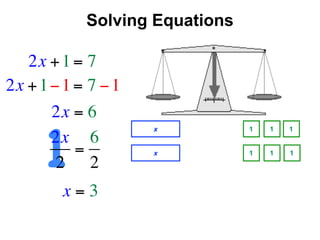
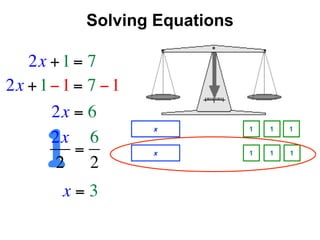
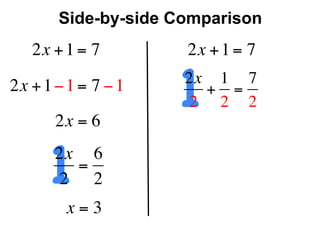
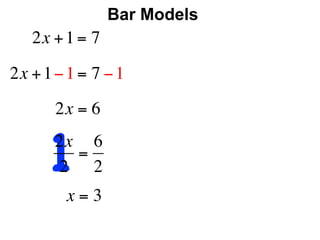
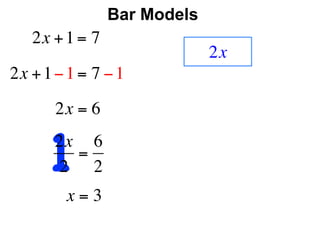
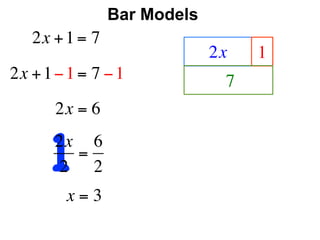
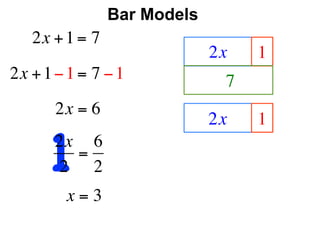
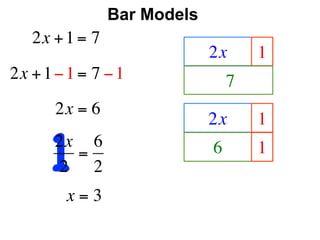
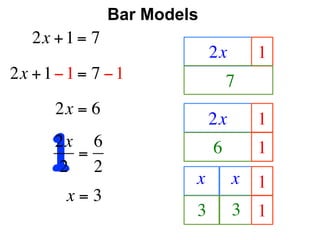
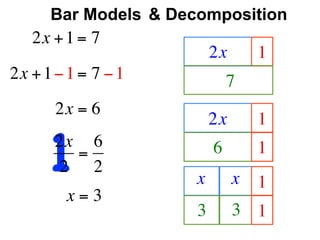
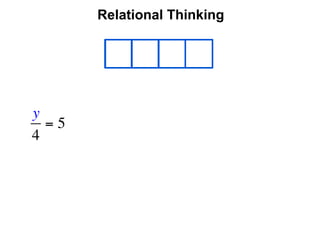
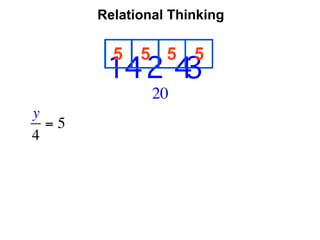
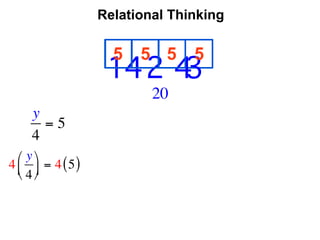
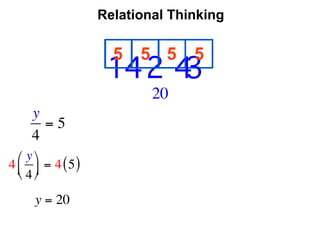
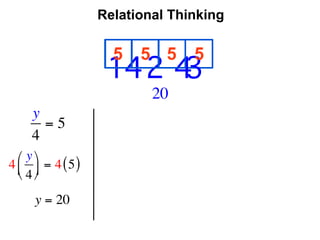
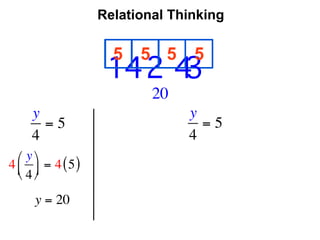
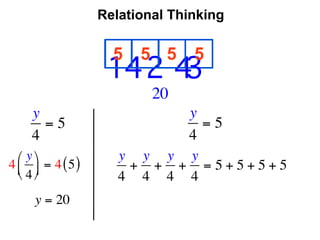
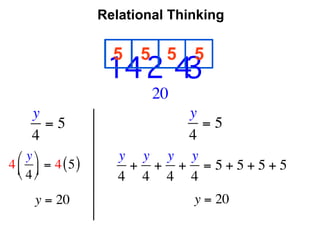
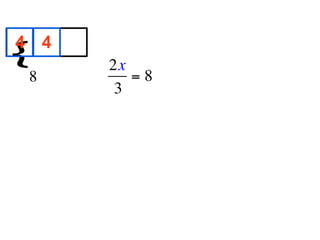
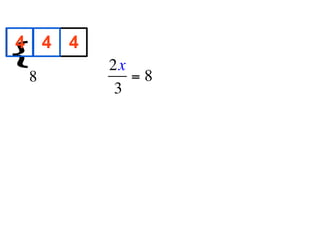
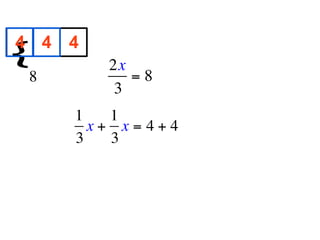
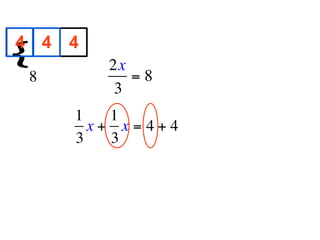
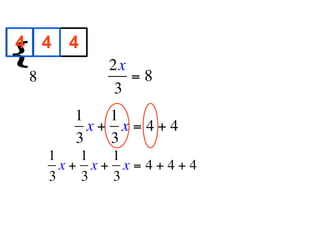
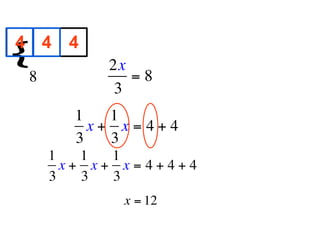
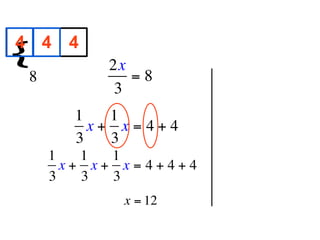
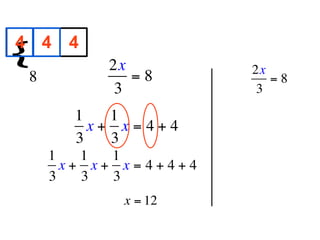
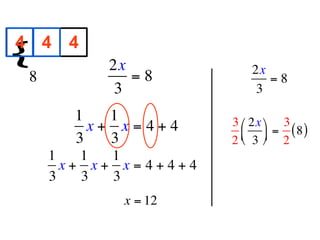
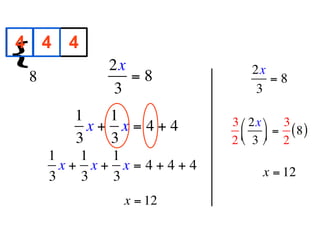
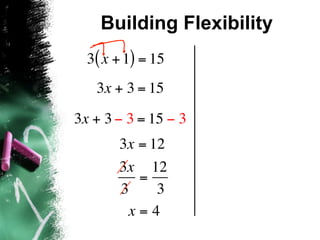
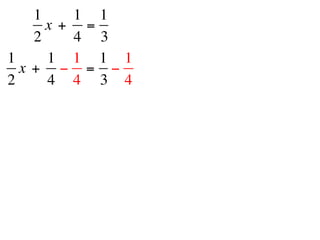
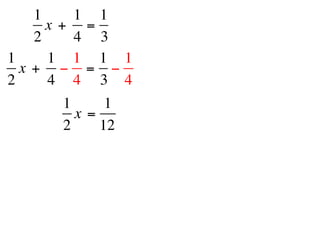
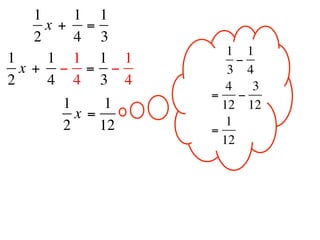
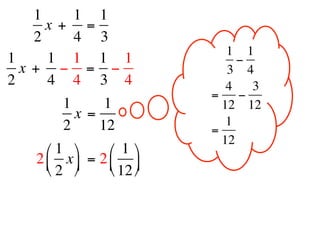
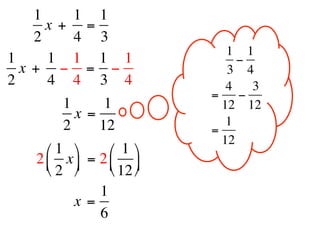
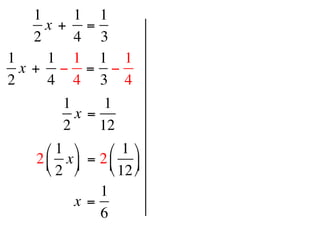
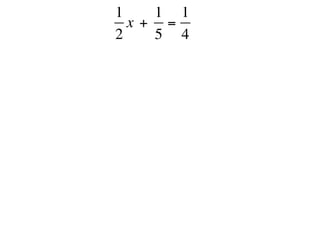
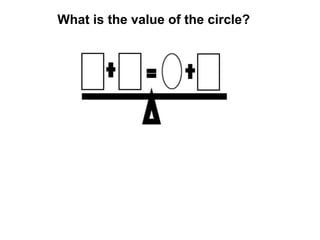
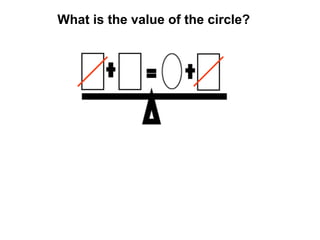
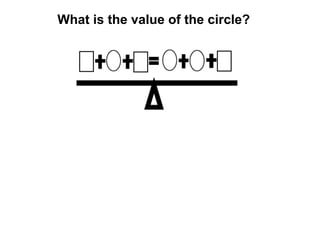
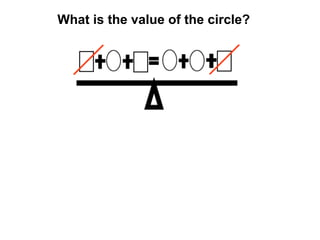
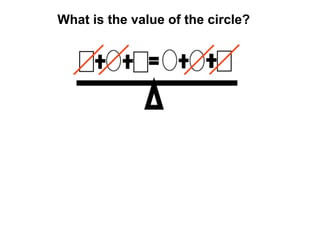
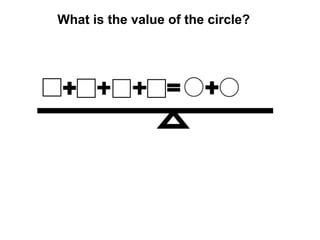
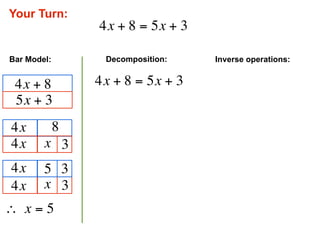
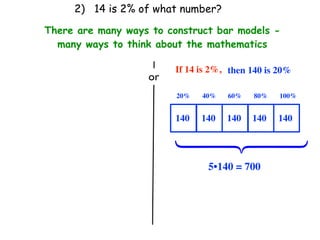
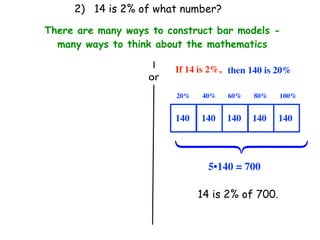
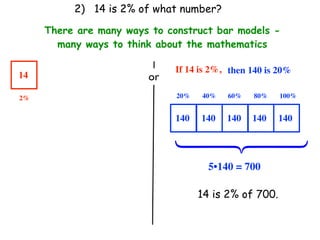
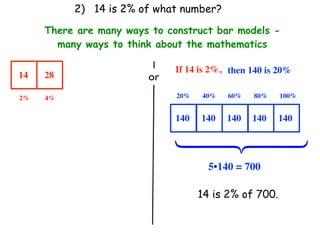
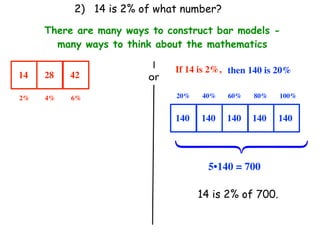
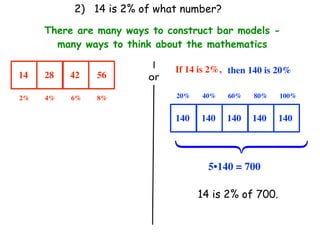
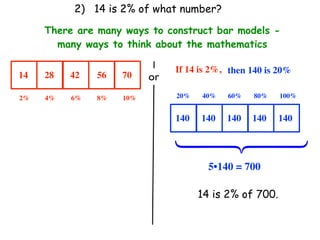
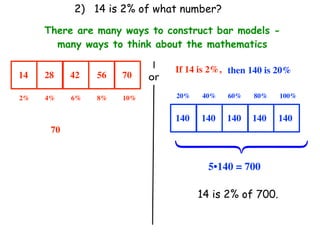
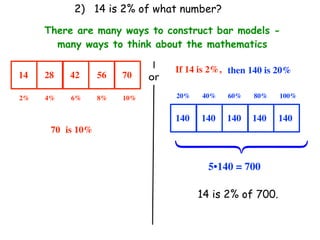
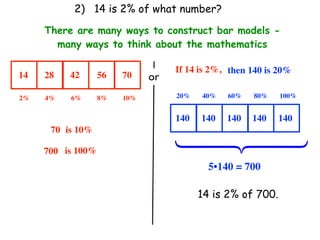
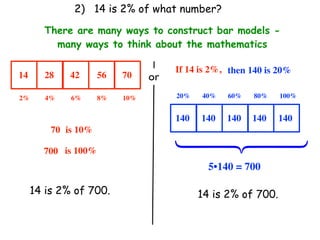
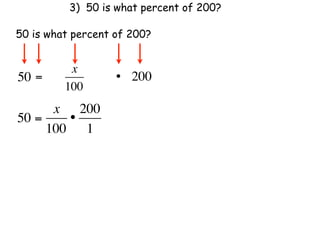
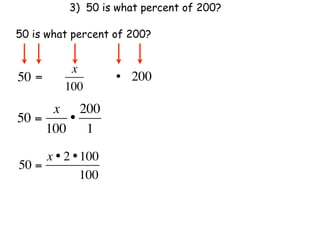
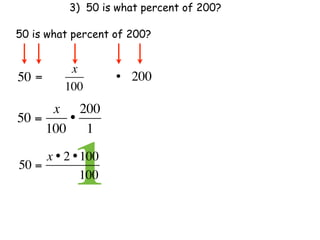
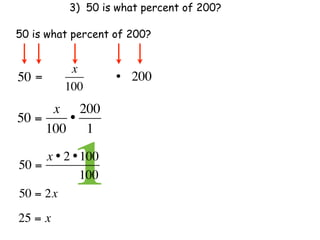
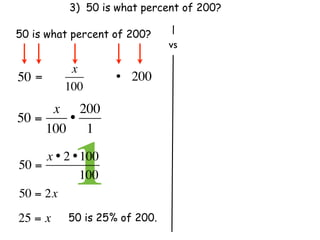
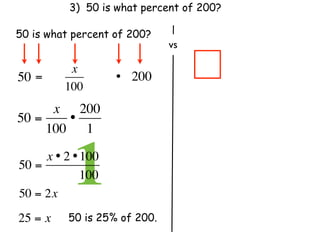
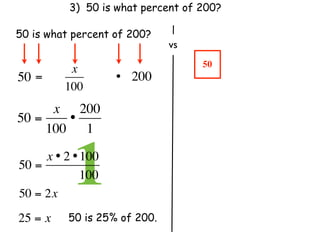
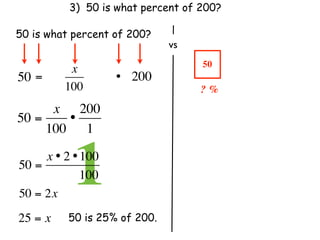
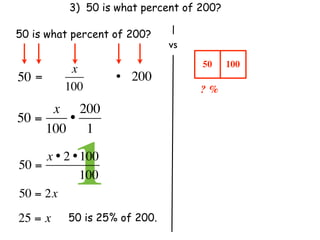
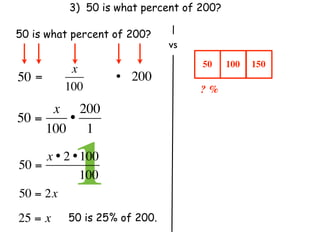
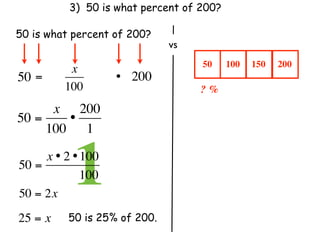
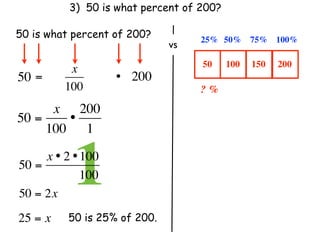
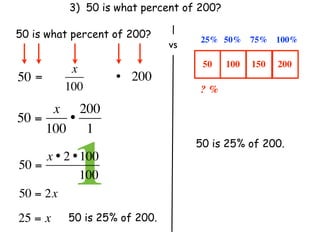
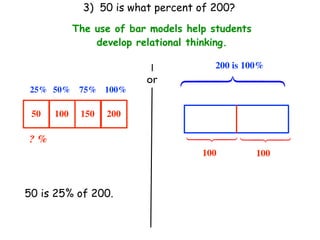
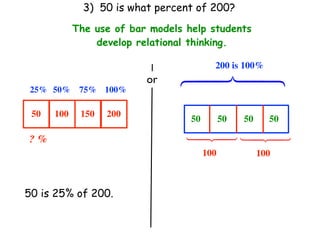
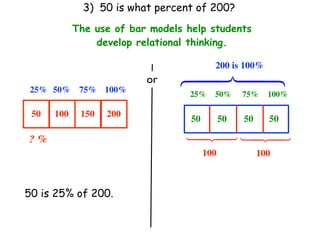
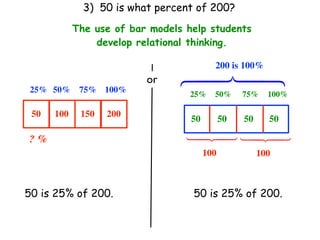
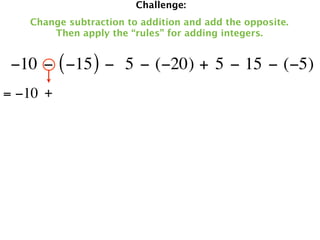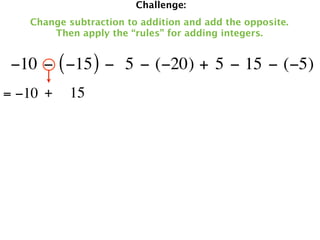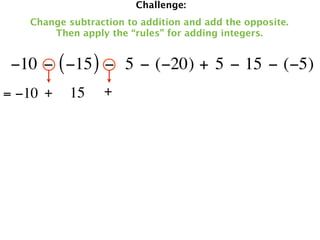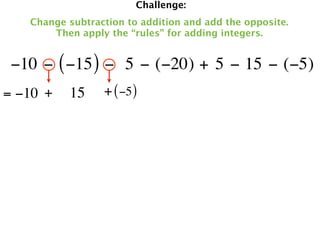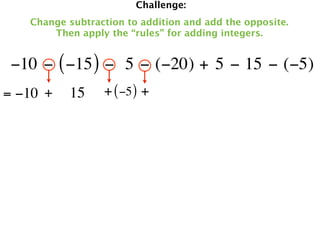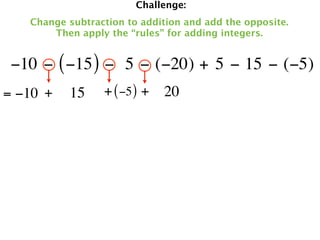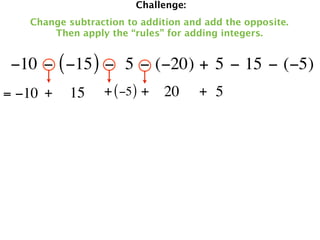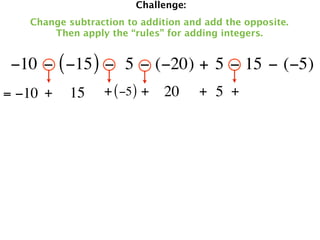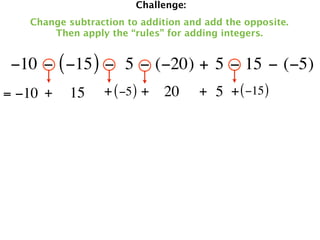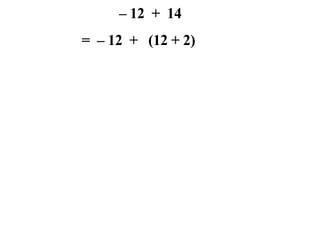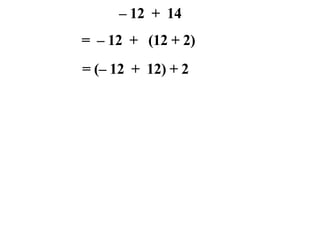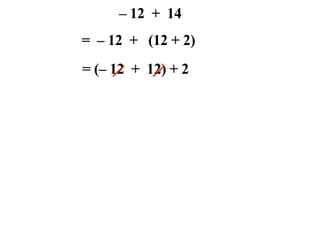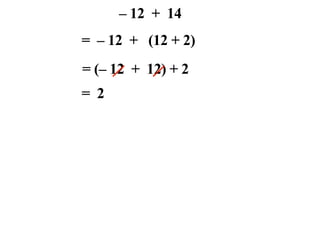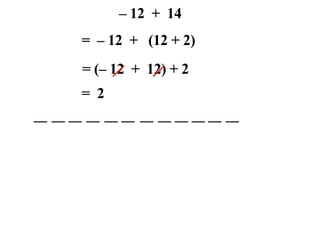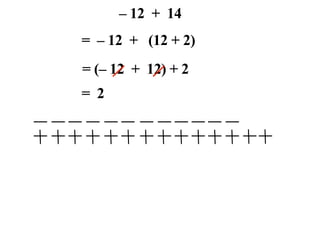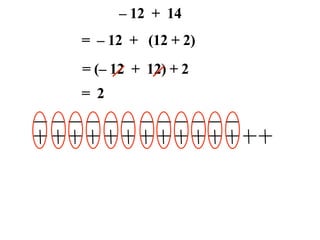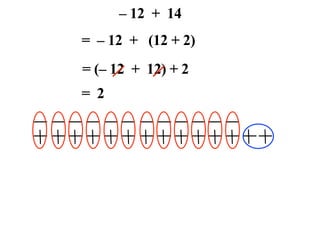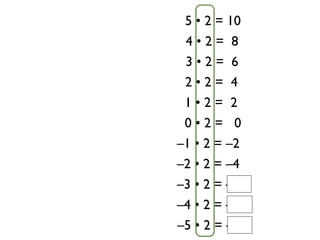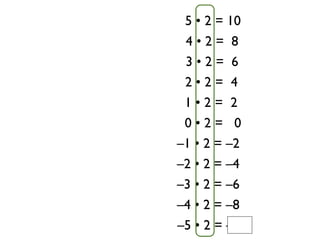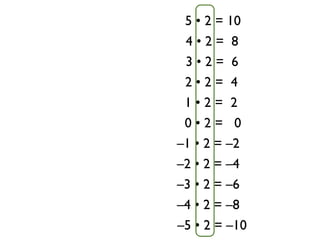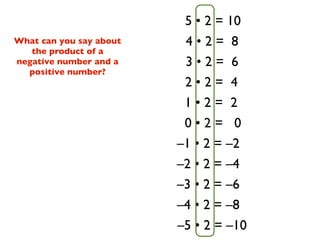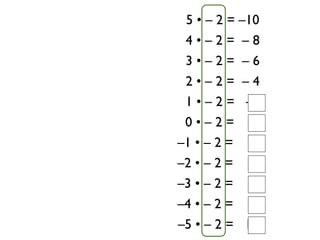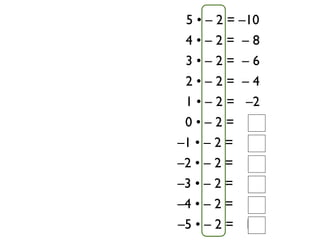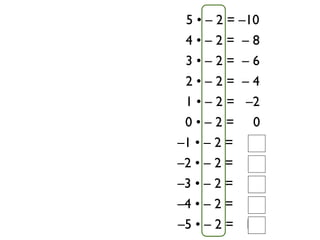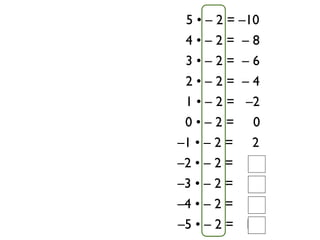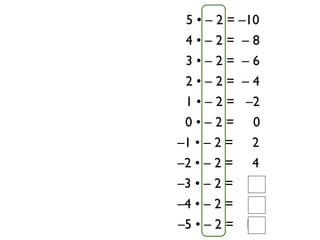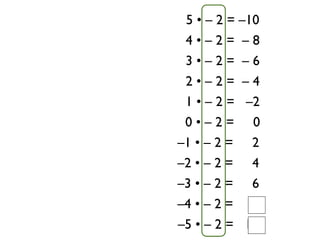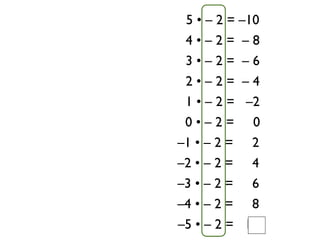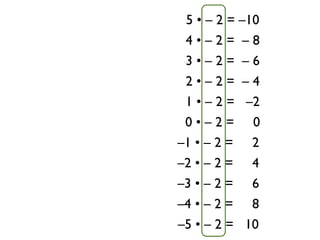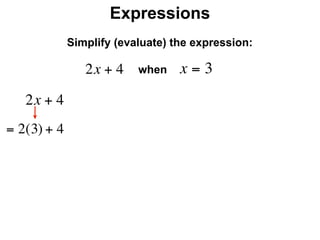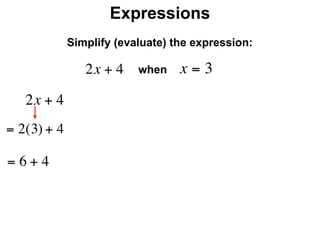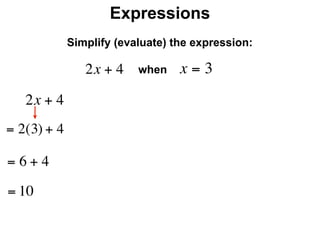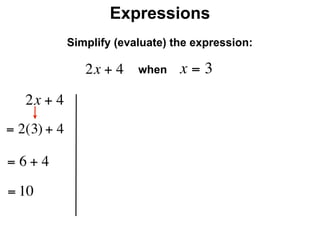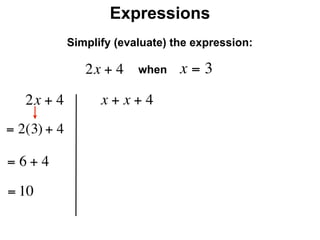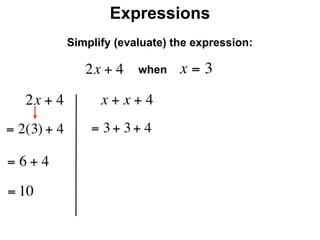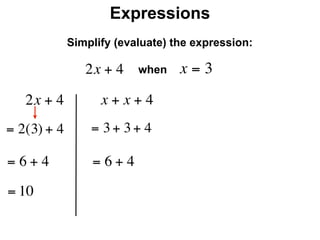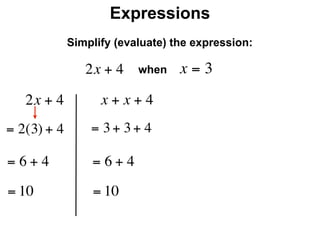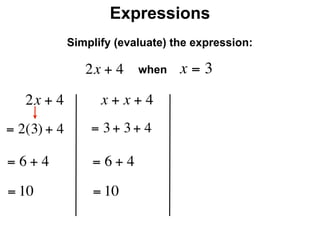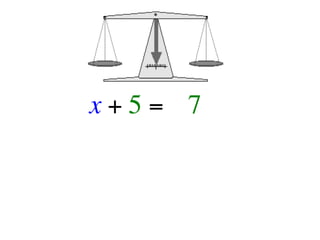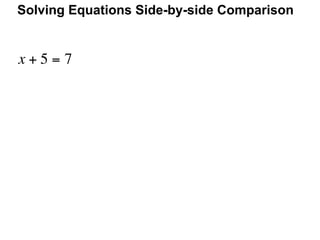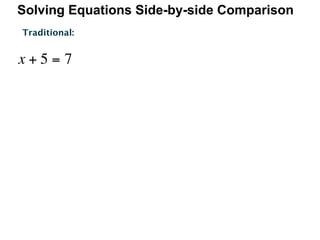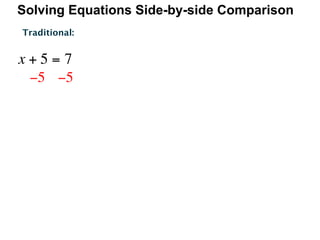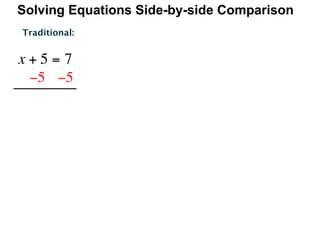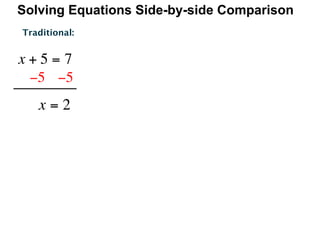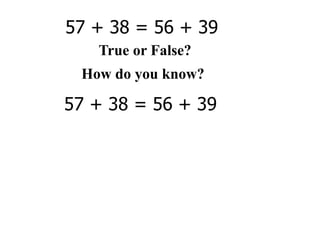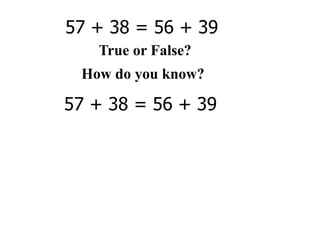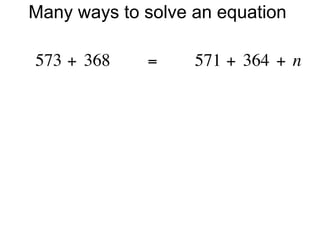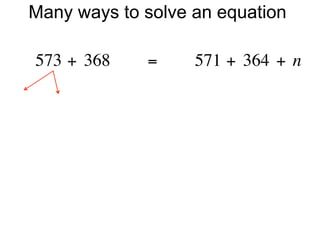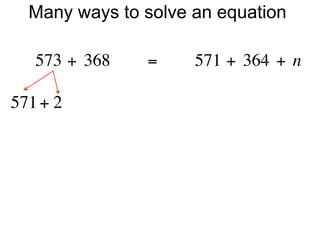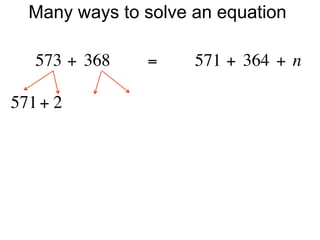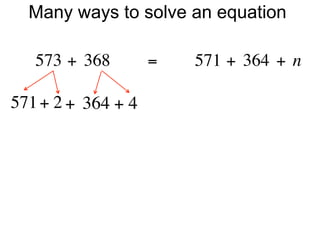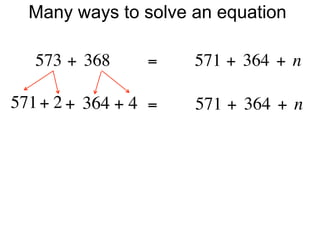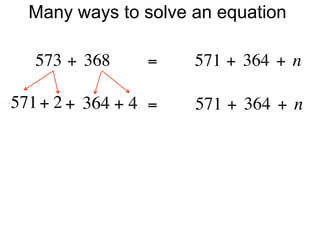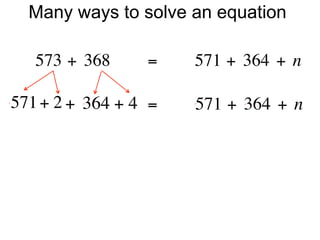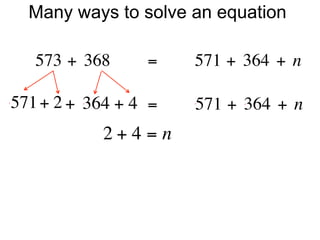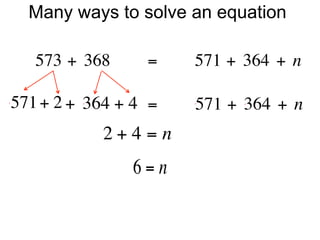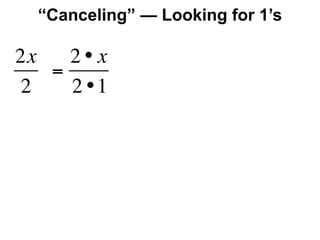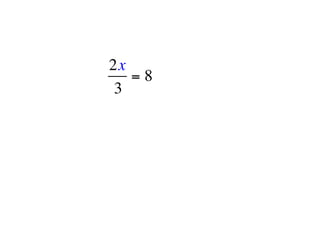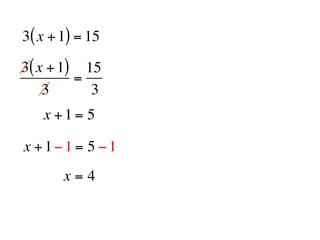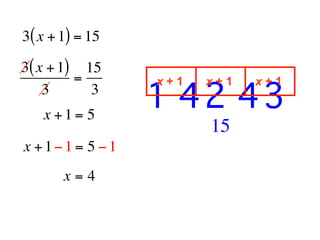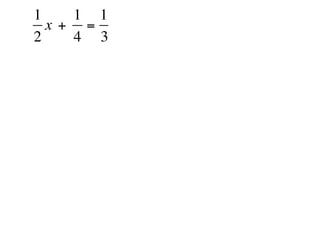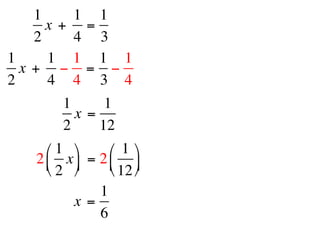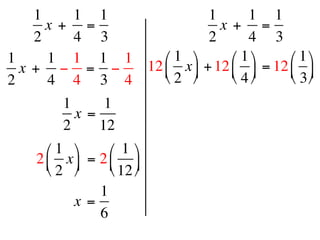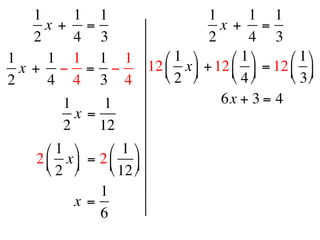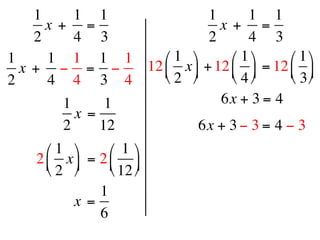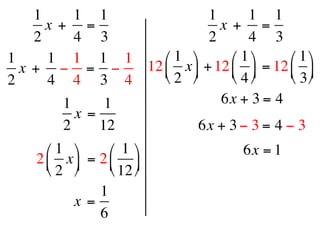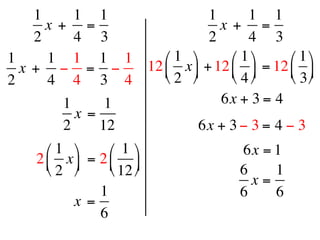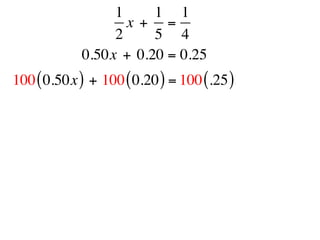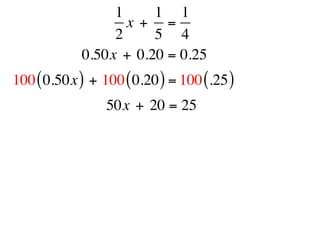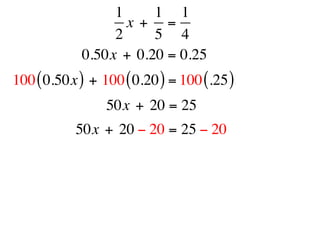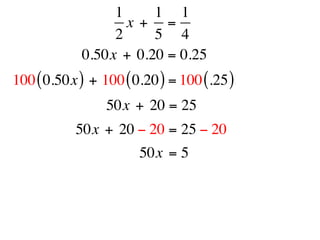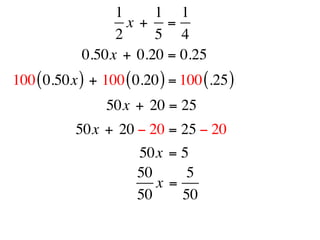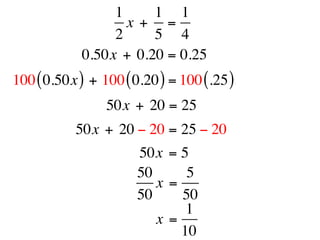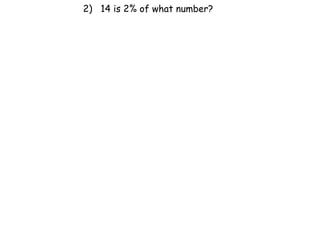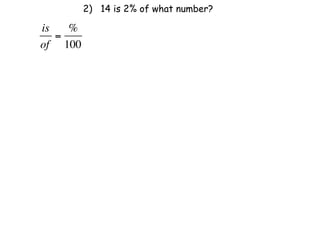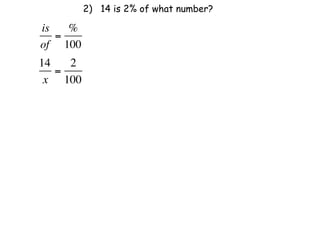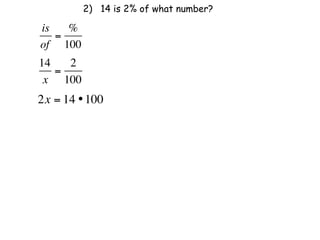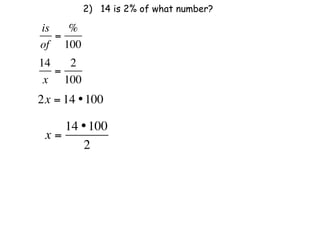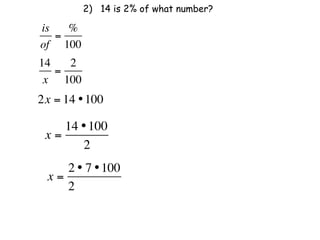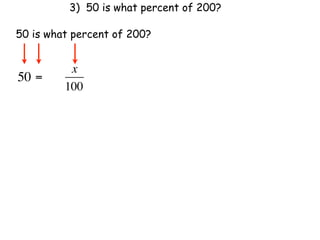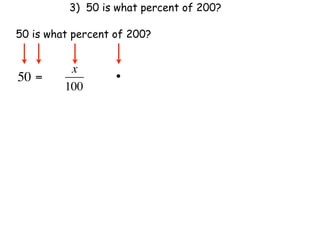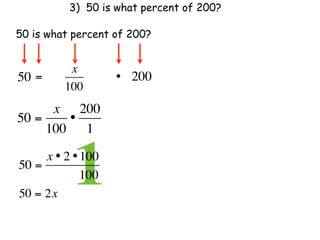The document describes a professional development session on adding integers using multiple representations. It shows expressions written out with numbers, number lines, and tile spacers to demonstrate the concepts of: - 3 + 5 = 8 - 3 + (-5) = -2 - -3 + 5 = 2 - -3 + (-5) = -8

1. San Leandro Unified
School District
Grades 3-5 Mathematics
Professional Development
March 2
4!– 3, 2000 + 3 + 3
Philip Gonsalves & Drew Kravin

2. Integer Operations –
Multiple Representations

3. Adding Integers – Multiple Representations

4. Adding Integers – Multiple Representations
Expressio
n

5. Adding Integers – Multiple Representations
Expressio
n
3+ 5 =

6. Adding Integers – Multiple Representations
Expressio
n
3+ 5 =
3 + ( −5 ) =

7. Adding Integers – Multiple Representations
Expressio
n
3+ 5 =
3 + ( −5 ) =
−3 + 5 =

8. Adding Integers – Multiple Representations
Expressio
n
3+ 5 =
3 + ( −5 ) =
−3 + 5 =
−3 + ( −5 ) =

9. Adding Integers – Multiple Representations
Expressio Number Line
n
3+ 5 =
3 + ( −5 ) =
−3 + 5 =
−3 + ( −5 ) =

10. Adding Integers – Multiple Representations
Expressio Number Line
n
3+ 5 =
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
3 + ( −5 ) =
−3 + 5 =
−3 + ( −5 ) =

11. Adding Integers – Multiple Representations
Expressio Number Line
n
3+ 5 =
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
3 + ( −5 ) =
−3 + 5 =
−3 + ( −5 ) =

12. Adding Integers – Multiple Representations
Expressio Number Line
n
3+ 5 =
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
3 + ( −5 ) =
−3 + 5 =
−3 + ( −5 ) =

13. Adding Integers – Multiple Representations
Expressio Number Line Tile Spacers
n
3+ 5 =
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
3 + ( −5 ) =
−3 + 5 =
−3 + ( −5 ) =

14. Adding Integers – Multiple Representations
Expressio Number Line Tile Spacers
n
3+ 5 =
+++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
3 + ( −5 ) =
−3 + 5 =
−3 + ( −5 ) =

15. Adding Integers – Multiple Representations
Expressio Number Line Tile Spacers
n
3+ 5 =
+++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
3 + ( −5 ) =
−3 + 5 =
−3 + ( −5 ) =

16. Adding Integers – Multiple Representations
Expressio Number Line Tile Spacers
n
3+ 5 = 8
+++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
3 + ( −5 ) =
−3 + 5 =
−3 + ( −5 ) =

17. Adding Integers – Multiple Representations
Expressio Number Line Tile Spacers
n
3+ 5 = 8
+++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
3 + ( −5 ) =
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
−3 + 5 =
−3 + ( −5 ) =

18. Adding Integers – Multiple Representations
Expressio Number Line Tile Spacers
n
3+ 5 = 8
+++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
3 + ( −5 ) =
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
−3 + 5 =
−3 + ( −5 ) =

19. Adding Integers – Multiple Representations
Expressio Number Line Tile Spacers
n
3+ 5 = 8
+++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
3 + ( −5 ) =
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
−3 + 5 =
−3 + ( −5 ) =

20. Adding Integers – Multiple Representations
Expressio Number Line Tile Spacers
n
3+ 5 = 8
+++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
3 + ( −5 ) = +++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
−3 + 5 =
−3 + ( −5 ) =

21. Adding Integers – Multiple Representations
Expressio Number Line Tile Spacers
n
3+ 5 = 8
+++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
3 + ( −5 ) = +++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 – ––––
−3 + 5 =
−3 + ( −5 ) =

22. Adding Integers – Multiple Representations
Expressio Number Line Tile Spacers
n
3+ 5 = 8
+++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
3 + ( −5 ) = +++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 – ––––
−3 + 5 =
−3 + ( −5 ) =

23. Adding Integers – Multiple Representations
Expressio Number Line Tile Spacers
n
3+ 5 = 8
+++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
3 + ( −5 ) = –2 +++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 – ––––
−3 + 5 =
−3 + ( −5 ) =

24. Adding Integers – Multiple Representations
Expressio Number Line Tile Spacers
n
3+ 5 = 8
+++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
3 + ( −5 ) = –2 +++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 – ––––
−3 + 5 =
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
−3 + ( −5 ) =

25. Adding Integers – Multiple Representations
Expressio Number Line Tile Spacers
n
3+ 5 = 8
+++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
3 + ( −5 ) = –2 +++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 – ––––
−3 + 5 =
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
−3 + ( −5 ) =

26. Adding Integers – Multiple Representations
Expressio Number Line Tile Spacers
n
3+ 5 = 8
+++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
3 + ( −5 ) = –2 +++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 – ––––
−3 + 5 =
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
−3 + ( −5 ) =

27. Adding Integers – Multiple Representations
Expressio Number Line Tile Spacers
n
3+ 5 = 8
+++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
3 + ( −5 ) = –2 +++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 – ––––
−3 + 5 = –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
−3 + ( −5 ) =

28. Adding Integers – Multiple Representations
Expressio Number Line Tile Spacers
n
3+ 5 = 8
+++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
3 + ( −5 ) = –2 +++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 – ––––
−3 + 5 = –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
−3 + ( −5 ) =

29. Adding Integers – Multiple Representations
Expressio Number Line Tile Spacers
n
3+ 5 = 8
+++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
3 + ( −5 ) = –2 +++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 – ––––
−3 + 5 = –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
−3 + ( −5 ) =

30. Adding Integers – Multiple Representations
Expressio Number Line Tile Spacers
n
3+ 5 = 8
+++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
3 + ( −5 ) = –2 +++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 – ––––
−3 + 5 = 2 –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
−3 + ( −5 ) =

31. Adding Integers – Multiple Representations
Expressio Number Line Tile Spacers
n
3+ 5 = 8
+++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
3 + ( −5 ) = –2 +++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 – ––––
−3 + 5 = 2 –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
−3 + ( −5 ) =
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8

32. Adding Integers – Multiple Representations
Expressio Number Line Tile Spacers
n
3+ 5 = 8
+++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
3 + ( −5 ) = –2 +++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 – ––––
−3 + 5 = 2 –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
−3 + ( −5 ) =
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8

33. Adding Integers – Multiple Representations
Expressio Number Line Tile Spacers
n
3+ 5 = 8
+++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
3 + ( −5 ) = –2 +++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 – ––––
−3 + 5 = 2 –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
−3 + ( −5 ) =
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8

34. Adding Integers – Multiple Representations
Expressio Number Line Tile Spacers
n
3+ 5 = 8
+++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
3 + ( −5 ) = –2 +++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 – ––––
−3 + 5 = 2 –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
−3 + ( −5 ) = –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8

35. Adding Integers – Multiple Representations
Expressio Number Line Tile Spacers
n
3+ 5 = 8
+++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
3 + ( −5 ) = –2 +++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 – ––––
−3 + 5 = 2 –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
−3 + ( −5 ) = –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 –– –––

36. Adding Integers – Multiple Representations
Expressio Number Line Tile Spacers
n
3+ 5 = 8
+++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
3 + ( −5 ) = –2 +++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 – ––––
−3 + 5 = 2 –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +++++
−3 + ( −5 ) = −8 –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 –– –––

37. Discovering the “Rules for Adding Integers”
3+ 5 =
3 + ( −5 ) =
−3 + 5 =
−3 + ( −5 ) =

38. Discovering the “Rules for Adding Integers”
3+ 5 =
3 + ( −5 ) =
−3 + 5 =
−3 + ( −5 ) =

39. Discovering the “Rules for Adding Integers”
3+ 5 = −3 + ( −5 ) =
3 + ( −5 ) =
−3 + 5 =

40. Discovering the “Rules for Adding Integers”
Same
Signs 3+ 5 = −3 + ( −5 ) =
3 + ( −5 ) =
−3 + 5 =

41. Discovering the “Rules for Adding Integers”
Same
Signs 3+ 5 = −3 + ( −5 ) =
−3 + 5 = 3 + ( −5 ) =

42. Discovering the “Rules for Adding Integers”
Same
Signs 3+ 5 = −3 + ( −5 ) =
3 + ( −5 ) = −3 + 5 =

43. Discovering the “Rules for Adding Integers”
Same
Signs 3+ 5 = −3 + ( −5 ) =
Different
Signs 3 + ( −5 ) = −3 + 5 =

44. Discovering the “Rules for Adding Integers”
Same
Signs 3+ 5 = −3 + ( −5 ) =
+++
+++++
Different
Signs 3 + ( −5 ) = −3 + 5 =

45. Discovering the “Rules for Adding Integers”
Same
Signs 3+ 5 = −3 + ( −5 ) =
+++ –––
+++++ –– –––
Different
Signs 3 + ( −5 ) = −3 + 5 =

46. Discovering the “Rules for Adding Integers”
Same
Signs 3+ 5 = 8 −3 + ( −5 ) =
+++ –––
+++++ –– –––
Different
Signs 3 + ( −5 ) = −3 + 5 =

47. Discovering the “Rules for Adding Integers”
Same
Signs 3+ 5 = 8 −3 + ( −5 ) = −8
+++ –––
+++++ –– –––
Different
Signs 3 + ( −5 ) = −3 + 5 =

48. Discovering the “Rules for Adding Integers”
Same
Signs 3+ 5 = 8 −3 + ( −5 ) = −8
+++ –––
+++++ –– –––
“If the signs are the same,
Different
Signs 3 + ( −5 ) = −3 + 5 =

49. Discovering the “Rules for Adding Integers”
Same
Signs 3+ 5 = 8 −3 + ( −5 ) = −8
+++ –––
+++++ –– –––
“If the signs are the same,
add the numbers (absolute value) and keep the sign”.
Different
Signs 3 + ( −5 ) = −3 + 5 =

50. Discovering the “Rules for Adding Integers”
Same
Signs 3+ 5 = 8 −3 + ( −5 ) = −8
+++ –––
+++++ –– –––
“If the signs are the same,
add the numbers (absolute value) and keep the sign”.
Different
Signs 3 + ( −5 ) = −3 + 5 =
+++
– ––––

51. Discovering the “Rules for Adding Integers”
Same
Signs 3+ 5 = 8 −3 + ( −5 ) = −8
+++ –––
+++++ –– –––
“If the signs are the same,
add the numbers (absolute value) and keep the sign”.
Different
Signs 3 + ( −5 ) = −3 + 5 =
+++ –––
– –––– +++++

52. Discovering the “Rules for Adding Integers”
Same
Signs 3+ 5 = 8 −3 + ( −5 ) = −8
+++ –––
+++++ –– –––
“If the signs are the same,
add the numbers (absolute value) and keep the sign”.
Different
Signs 3 + ( −5 ) = –2 −3 + 5 =
+++ –––
– –––– +++++

53. Discovering the “Rules for Adding Integers”
Same
Signs 3+ 5 = 8 −3 + ( −5 ) = −8
+++ –––
+++++ –– –––
“If the signs are the same,
add the numbers (absolute value) and keep the sign”.
Different
Signs 3 + ( −5 ) = –2 −3 + 5 = 2
+++ –––
– –––– +++++

54. Discovering the “Rules for Adding Integers”
Same
Signs 3+ 5 = 8 −3 + ( −5 ) = −8
+++ –––
+++++ –– –––
“If the signs are the same,
add the numbers (absolute value) and keep the sign”.
Different
Signs 3 + ( −5 ) = –2 −3 + 5 = 2
+++ –––
– –––– +++++
“If the signs are different,

55. Discovering the “Rules for Adding Integers”
Same
Signs 3+ 5 = 8 −3 + ( −5 ) = −8
+++ –––
+++++ –– –––
“If the signs are the same,
add the numbers (absolute value) and keep the sign”.
Different
Signs 3 + ( −5 ) = –2 −3 + 5 = 2
+++ –––
– –––– +++++
“If the signs are different,
subtract the numbers (absolute value)

56. Discovering the “Rules for Adding Integers”
Same
Signs 3+ 5 = 8 −3 + ( −5 ) = −8
+++ –––
+++++ –– –––
“If the signs are the same,
add the numbers (absolute value) and keep the sign”.
Different
Signs 3 + ( −5 ) = –2 −3 + 5 = 2
+++ –––
– –––– +++++
“If the signs are different,
subtract the numbers (absolute value)
and keep the sign of what you have the most of”.

57. Subtracting Integers –
Multiple Representations
Guided Discovery

58. Subtracting Integers

59. Subtracting Integers
Expressio
n

60. Subtracting Integers
Expressio
n
3− 5 =

61. Subtracting Integers
Expressio
n
3− 5 =

62. Subtracting Integers
Expressio
n
3− 5 =
3 + ( −5 ) =

63. Subtracting Integers
Expressio Number Line
n
3− 5 =
3 + ( −5 ) =

64. Subtracting Integers
Expressio Number Line
n
3− 5 =
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
3 + ( −5 ) =

65. Subtracting Integers
Expressio Number Line
n
3− 5 =
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
3 + ( −5 ) =

66. Subtracting Integers
Expressio Number Line
n
3− 5 =
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
3 + ( −5 ) =

67. Subtracting Integers
Expressio Number Line
n
3 − 5 = −2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
3 + ( −5 ) =

68. Subtracting Integers
Expressio Number Line
n
3 − 5 = −2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
3 + ( −5 ) =
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8

69. Subtracting Integers
Expressio Number Line
n
3 − 5 = −2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
3 + ( −5 ) =
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8

70. Subtracting Integers
Expressio Number Line
n
3 − 5 = −2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
3 + ( −5 ) =
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8

71. Subtracting Integers
Expressio Number Line
n
3 − 5 = −2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
3 + ( −5 ) = –2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8

72. Subtracting Integers
Expressio Number Line
n
3 − 5 = −2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
3 + ( −5 ) = –2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8

73. Subtracting Integers
Expressio Number Line
n
3 − 5 = −2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
3 + ( −5 ) = –2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
Notice – same
movement, same
answer, equivalent
expressions

74. Subtracting Integers
Expressio Number Line
n
3 − 5 = −2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
3 + ( −5 ) = –2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
Notice – same 3− 5
movement, same
answer, equivalent
expressions

75. Subtracting Integers
Expressio Number Line
n
3 − 5 = −2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
3 + ( −5 ) = –2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
Notice – same 3− 5
movement, same
answer, equivalent
expressions
To subtract integers, change subtraction to addition

76. Subtracting Integers
Expressio Number Line
n
3 − 5 = −2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
3 + ( −5 ) = –2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
Notice – same 3− 5
movement, same
answer, equivalent
expressions =3+
To subtract integers, change subtraction to addition

77. Subtracting Integers
Expressio Number Line
n
3 − 5 = −2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
3 + ( −5 ) = –2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
Notice – same 3− 5
movement, same
answer, equivalent
expressions = 3 + ( −5 )
To subtract integers, change subtraction to addition
and add the opposite.

78. Subtracting Integers
Expressio Number Line
n
3 − 5 = −2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
3 + ( −5 ) = –2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
Notice – same 3− 5
movement, same
answer, equivalent
expressions = 3 + ( −5 )
To subtract integers, change subtraction to addition
and add the opposite.
Then apply the “rules” for adding integers.

79. Subtracting Integers
Expressio Number Line
n
3 − 5 = −2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
3 + ( −5 ) = –2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
Notice – same 3− 5
movement, same
answer, equivalent
expressions = 3 + ( −5 )
= −2
To subtract integers, change subtraction to addition
and add the opposite.
Then apply the “rules” for adding integers.

80. Subtracting Integers
Expressio Number Line Tile Spacers
n
3 − 5 = −2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
3 + ( −5 ) = –2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
Notice – same 3− 5
movement, same
answer, equivalent
expressions = 3 + ( −5 )
= −2
To subtract integers, change subtraction to addition
and add the opposite.
Then apply the “rules” for adding integers.

81. Subtracting Integers
Expressio Number Line Tile Spacers
n
++ +
3 − 5 = −2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
3 + ( −5 ) = –2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
Notice – same 3− 5
movement, same
answer, equivalent
expressions = 3 + ( −5 )
= −2
To subtract integers, change subtraction to addition
and add the opposite.
Then apply the “rules” for adding integers.

82. Subtracting Integers
Expressio Number Line Tile Spacers
n
++ +
3 − 5 = −2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 –
+
3 + ( −5 ) = –2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
Notice – same 3− 5
movement, same
answer, equivalent
expressions = 3 + ( −5 )
= −2
To subtract integers, change subtraction to addition
and add the opposite.
Then apply the “rules” for adding integers.

83. Subtracting Integers
Expressio Number Line Tile Spacers
n
++ +
3 − 5 = −2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 ––
++
3 + ( −5 ) = –2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
Notice – same 3− 5
movement, same
answer, equivalent
expressions = 3 + ( −5 )
= −2
To subtract integers, change subtraction to addition
and add the opposite.
Then apply the “rules” for adding integers.

84. Subtracting Integers
Expressio Number Line Tile Spacers
n
++ +
3 − 5 = −2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 ––
++
3 + ( −5 ) = –2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
Notice – same 3− 5
movement, same
answer, equivalent
expressions = 3 + ( −5 )
= −2
To subtract integers, change subtraction to addition
and add the opposite.
Then apply the “rules” for adding integers.

85. Subtracting Integers
Expressio Number Line Tile Spacers
n
++ +
3 − 5 = −2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 ––
++
3 + ( −5 ) = –2
+++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
Notice – same 3− 5
movement, same
answer, equivalent
expressions = 3 + ( −5 )
= −2
To subtract integers, change subtraction to addition
and add the opposite.
Then apply the “rules” for adding integers.

86. Subtracting Integers
Expressio Number Line Tile Spacers
n
++ +
3 − 5 = −2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 ––
++
3 + ( −5 ) = –2
+++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 –––––
Notice – same 3− 5
movement, same
answer, equivalent
expressions = 3 + ( −5 )
= −2
To subtract integers, change subtraction to addition
and add the opposite.
Then apply the “rules” for adding integers.

87. Subtracting Integers
Expressio Number Line Tile Spacers
n
++ +
3 − 5 = −2
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 ––
++
3 + ( −5 ) = –2
+++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 –––––
Notice – same 3− 5
movement, same
answer, equivalent
expressions = 3 + ( −5 )
= −2
To subtract integers, change subtraction to addition
and add the opposite.
Then apply the “rules” for adding integers.

88. You Try:

89. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
−2 − 5
−2 − ( −5 )

90. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
−2 − 5
−2 − ( −5 )

91. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
−2 − 5
−2 − ( −5 )

92. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
−2 − 5
−2 − ( −5 )

93. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
−2 − 5
−2 − ( −5 )

94. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
–
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+
−2 − 5
−2 − ( −5 )

95. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
++
−2 − 5
−2 − ( −5 )

96. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
–––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
−2 − 5
−2 − ( −5 )

97. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
–––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
−2 − 5
−2 − ( −5 )

98. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
= 2 + ( −5 ) –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
−2 − 5
−2 − ( −5 )

99. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
= 2 + ( −5 ) –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
= –3
−2 − 5
−2 − ( −5 )

100. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
= 2 + ( −5 ) –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
= –3
−2 − 5
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
−2 − ( −5 )

101. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
= 2 + ( −5 ) –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
= –3
−2 − 5
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
−2 − ( −5 )

102. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
= 2 + ( −5 ) –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
= –3
−2 − 5
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
−2 − ( −5 )

103. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
= 2 + ( −5 ) –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
= –3
−2 − 5 −−
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
−2 − ( −5 )

104. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
= 2 + ( −5 ) –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
= –3
−2 − 5 −−
–
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 +
−2 − ( −5 )

105. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
= 2 + ( −5 ) –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
= –3
−2 − 5 −−
––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 + +
−2 − ( −5 )

106. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
= 2 + ( −5 ) –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
= –3
−2 − 5 −−
–––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 + ++
−2 − ( −5 )

107. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
= 2 + ( −5 ) –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
= –3
−2 − 5 −−
––––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 + ++ +
−2 − ( −5 )

108. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
= 2 + ( −5 ) –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
= –3
−2 − 5 −−
–––––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 + ++ + +
−2 − ( −5 )

109. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
= 2 + ( −5 ) –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
= –3
−2 − 5 −−
–––––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 + ++ + +
−2 − ( −5 )

110. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
= 2 + ( −5 ) –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
= –3
−2 − 5 −−
–––––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 + ++ + +
−2 − ( −5 )

111. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
= 2 + ( −5 ) –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
= –3
−2 − 5 −−
= −2 + ( −5 ) –––––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 + ++ + +
−2 − ( −5 )

112. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
= 2 + ( −5 ) –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
= –3
−2 − 5 −−
= −2 + ( −5 ) –––––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 + ++ + +
= −7
−2 − ( −5 )

113. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
= 2 + ( −5 ) –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
= –3
−2 − 5 −−
= −2 + ( −5 ) –––––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 + ++ + +
= −7
−2 − ( −5 )
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8

114. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
= 2 + ( −5 ) –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
= –3
−2 − 5 −−
= −2 + ( −5 ) –––––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 + ++ + +
= −7
−2 − ( −5 )
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8

115. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
= 2 + ( −5 ) –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
= –3
−2 − 5 −−
= −2 + ( −5 ) –––––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 + ++ + +
= −7
−2 − ( −5 )
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8

116. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
= 2 + ( −5 ) –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
= –3
−2 − 5 −−
= −2 + ( −5 ) –––––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 + ++ + +
= −7
−2 − ( −5 ) ––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8

117. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
= 2 + ( −5 ) –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
= –3
−2 − 5 −−
= −2 + ( −5 ) –––––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 + ++ + +
= −7
−2 − ( −5 ) ––
–
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+

118. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
= 2 + ( −5 ) –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
= –3
−2 − 5 −−
= −2 + ( −5 ) –––––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 + ++ + +
= −7
−2 − ( −5 ) ––
––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+ +

119. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
= 2 + ( −5 ) –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
= –3
−2 − 5 −−
= −2 + ( −5 ) –––––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 + ++ + +
= −7
−2 − ( −5 ) ––
–––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+ + +

120. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
= 2 + ( −5 ) –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
= –3
−2 − 5 −−
= −2 + ( −5 ) –––––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 + ++ + +
= −7
−2 − ( −5 ) ––
–––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+ + +

121. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
= 2 + ( −5 ) –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
= –3
−2 − 5 −−
= −2 + ( −5 ) –––––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 + ++ + +
= −7
−2 − ( −5 ) ––
= −2 + 5
–––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+ + +

122. You Try:
Expressio Number Line Tile Spacers
n
2 − 5
++
= 2 + ( −5 ) –––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+++
= –3
−2 − 5 −−
= −2 + ( −5 ) –––––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 + ++ + +
= −7
−2 − ( −5 ) ––
= −2 + 5
–––
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
+ + +
=3

123. Challenge:

124. Challenge:
Change subtraction to addition and add the opposite.
Then apply the “rules” for adding integers.

125. Challenge:
Change subtraction to addition and add the opposite.
Then apply the “rules” for adding integers.
−10 − ( −15 ) − 5 − (−20) + 5 − 15 − (−5)

126. Challenge:
Change subtraction to addition and add the opposite.
Then apply the “rules” for adding integers.
−10 − ( −15 ) − 5 − (−20) + 5 − 15 − (−5)
= −10

127. Challenge:
Change subtraction to addition and add the opposite.
Then apply the “rules” for adding integers.
−10 − ( −15 ) − 5 − (−20) + 5 − 15 − (−5)
= −10 +

128. Challenge:
Change subtraction to addition and add the opposite.
Then apply the “rules” for adding integers.
−10 − ( −15 ) − 5 − (−20) + 5 − 15 − (−5)
= −10 + 15

129. Challenge:
Change subtraction to addition and add the opposite.
Then apply the “rules” for adding integers.
−10 − ( −15 ) − 5 − (−20) + 5 − 15 − (−5)
= −10 + 15 +

130. Challenge:
Change subtraction to addition and add the opposite.
Then apply the “rules” for adding integers.
−10 − ( −15 ) − 5 − (−20) + 5 − 15 − (−5)
= −10 + 15 + ( −5 )

131. Challenge:
Change subtraction to addition and add the opposite.
Then apply the “rules” for adding integers.
−10 − ( −15 ) − 5 − (−20) + 5 − 15 − (−5)
= −10 + 15 + ( −5 ) +

132. Challenge:
Change subtraction to addition and add the opposite.
Then apply the “rules” for adding integers.
−10 − ( −15 ) − 5 − (−20) + 5 − 15 − (−5)
= −10 + 15 + ( −5 ) + 20

133. Challenge:
Change subtraction to addition and add the opposite.
Then apply the “rules” for adding integers.
−10 − ( −15 ) − 5 − (−20) + 5 − 15 − (−5)
= −10 + 15 + ( −5 ) + 20 + 5

134. Challenge:
Change subtraction to addition and add the opposite.
Then apply the “rules” for adding integers.
−10 − ( −15 ) − 5 − (−20) + 5 − 15 − (−5)
= −10 + 15 + ( −5 ) + 20 + 5 +

135. Challenge:
Change subtraction to addition and add the opposite.
Then apply the “rules” for adding integers.
−10 − ( −15 ) − 5 − (−20) + 5 − 15 − (−5)
= −10 + 15 + ( −5 ) + 20 + 5 + ( −15 )

136. Challenge:
Change subtraction to addition and add the opposite.
Then apply the “rules” for adding integers.
−10 − ( −15 ) − 5 − (−20) + 5 − 15 − (−5)
= −10 + 15 + ( −5 ) + 20 + 5 + ( −15 ) +

137. Challenge:
Change subtraction to addition and add the opposite.
Then apply the “rules” for adding integers.
−10 − ( −15 ) − 5 − (−20) + 5 − 15 − (−5)
= −10 + 15 + ( −5 ) + 20 + 5 + ( −15 ) + 5

138. Challenge:
Change subtraction to addition and add the opposite.
Then apply the “rules” for adding integers.
−10 − ( −15 ) − 5 − (−20) + 5 − 15 − (−5)
= −10 + 15 + ( −5 ) + 20 + 5 + ( −15 ) + 5

139. Challenge:
Change subtraction to addition and add the opposite.
Then apply the “rules” for adding integers.
−10 − ( −15 ) − 5 − (−20) + 5 − 15 − (−5)
= −10 + 15 + ( −5 ) + 20 + 5 + ( −15 ) + 5
= 45

140. Challenge:
Change subtraction to addition and add the opposite.
Then apply the “rules” for adding integers.
−10 − ( −15 ) − 5 − (−20) + 5 − 15 − (−5)
= −10 + 15 + ( −5 ) + 20 + 5 + ( −15 ) + 5
= 45

141. Challenge:
Change subtraction to addition and add the opposite.
Then apply the “rules” for adding integers.
−10 − ( −15 ) − 5 − (−20) + 5 − 15 − (−5)
= −10 + 15 + ( −5 ) + 20 + 5 + ( −15 ) + 5
= 45 + ( −30 )

142. Challenge:
Change subtraction to addition and add the opposite.
Then apply the “rules” for adding integers.
−10 − ( −15 ) − 5 − (−20) + 5 − 15 − (−5)
= −10 + 15 + ( −5 ) + 20 + 5 + ( −15 ) + 5
= 45 + ( −30 )
= 15

144. – 12 + 14

145. – 12 + 14
= – 12 + (12 + 2)

146. – 12 + 14
= – 12 + (12 + 2)
= (– 12 + 12) + 2

147. – 12 + 14
= – 12 + (12 + 2)
= (– 12 + 12) + 2

148. – 12 + 14
= – 12 + (12 + 2)
= (– 12 + 12) + 2
= 2

149. – 12 + 14
= – 12 + (12 + 2)
= (– 12 + 12) + 2
= 2

150. – 12 + 14
= – 12 + (12 + 2)
= (– 12 + 12) + 2
= 2

151. – 12 + 14
= – 12 + (12 + 2)
= (– 12 + 12) + 2
= 2

152. – 12 + 14
= – 12 + (12 + 2)
= (– 12 + 12) + 2
= 2

153. – 12 + 14
= – 12 + (12 + 2)
= (– 12 + 12) + 2
= 2

154. – 12 + 14
= – 12 + (12 + 2)
= (– 12 + 12) + 2
= 2
0

155. – 12 + 14
= – 12 + (12 + 2)
= (– 12 + 12) + 2
= 2
0

156. – 12 + 14
= – 12 + (12 + 2)
= (– 12 + 12) + 2
= 2
0

157. – 12 + 14
= – 12 + (12 + 2)
= (– 12 + 12) + 2
= 2
-12 0

158. – 12 + 14
= – 12 + (12 + 2)
= (– 12 + 12) + 2
= 2
-12
-12 0

159. – 12 + 14
= – 12 + (12 + 2)
= (– 12 + 12) + 2
= 2
-12
-12 0 2

160. – 12 + 14
= – 12 + (12 + 2)
= (– 12 + 12) + 2
= 2
14
-12
-12 0 2

161. Multiplying/Dividing
Integers

162. 5 • 2 = 10
4•2= 8
3•2= 6
2•2= 4
1•2= 2
0•2= 0
–1 • 2 = –2
–2 • 2 = –4
–3 • 2 = –6
–4 • 2 = –8
–5 • 2 = –10

163. 5 • 2 = 10
4•2= 8
3•2= 6
2•2= 4
1•2= 2
0•2= 0
–1 • 2 = –2
–2 • 2 = –4
–3 • 2 = –6
–4 • 2 = –8
–5 • 2 = –10

164. 5 • 2 = 10
4•2= 8
3•2= 6
2•2= 4
1•2= 2
0•2= 0
–1 • 2 = –2
–2 • 2 = –4
–3 • 2 = –6
–4 • 2 = –8
–5 • 2 = –10

165. 5 • 2 = 10
4•2= 8
3•2= 6
2•2= 4
1•2= 2
0•2= 0
–1 • 2 = –2
–2 • 2 = –4
–3 • 2 = –6
–4 • 2 = –8
–5 • 2 = –10

166. 5 • 2 = 10
4•2= 8
3•2= 6
2•2= 4
1•2= 2
0•2= 0
–1 • 2 = –2
–2 • 2 = –4
–3 • 2 = –6
–4 • 2 = –8
–5 • 2 = –10

167. 5 • 2 = 10
4•2= 8
3•2= 6
2•2= 4
1•2= 2
0•2= 0
–1 • 2 = –2
–2 • 2 = –4
–3 • 2 = –6
–4 • 2 = –8
–5 • 2 = –10

168. 5 • 2 = 10
4•2= 8
3•2= 6
2•2= 4
1•2= 2
0•2= 0
–1 • 2 = –2
–2 • 2 = –4
–3 • 2 = –6
–4 • 2 = –8
–5 • 2 = –10

169. 5 • 2 = 10
4•2= 8
3•2= 6
2•2= 4
1•2= 2
0•2= 0
–1 • 2 = –2
–2 • 2 = –4
–3 • 2 = –6
–4 • 2 = –8
–5 • 2 = –10

170. 5 • 2 = 10
4•2= 8
3•2= 6
2•2= 4
1•2= 2
0•2= 0
–1 • 2 = –2
–2 • 2 = –4
–3 • 2 = –6
–4 • 2 = –8
–5 • 2 = –10

171. 5 • 2 = 10
4•2= 8
3•2= 6
2•2= 4
1•2= 2
0•2= 0
–1 • 2 = –2
–2 • 2 = –4
–3 • 2 = –6
–4 • 2 = –8
–5 • 2 = –10

172. 5 • 2 = 10
4•2= 8
3•2= 6
2•2= 4
1•2= 2
0•2= 0
–1 • 2 = –2
–2 • 2 = –4
–3 • 2 = –6
–4 • 2 = –8
–5 • 2 = –10

173. 5 • 2 = 10
4•2= 8
3•2= 6
2•2= 4
1•2= 2
0•2= 0
–1 • 2 = –2
–2 • 2 = –4
–3 • 2 = –6
–4 • 2 = –8
–5 • 2 = –10

174. 5 • 2 = 10
4•2= 8
3•2= 6
2•2= 4
1•2= 2
0•2= 0
–1 • 2 = –2
–2 • 2 = –4
–3 • 2 = –6
–4 • 2 = –8
–5 • 2 = –10

175. 5 • 2 = 10
4•2= 8
3•2= 6
2•2= 4
1•2= 2
0•2= 0
–1 • 2 = –2
–2 • 2 = –4
–3 • 2 = –6
–4 • 2 = –8
–5 • 2 = –10

176. 5 • 2 = 10
4•2= 8
3•2= 6
2•2= 4
1•2= 2
0•2= 0
–1 • 2 = –2
–2 • 2 = –4
–3 • 2 = –6
–4 • 2 = –8
–5 • 2 = –10

177. 5 • 2 = 10
4•2= 8
3•2= 6
2•2= 4
1•2= 2
0•2= 0
–1 • 2 = –2
–2 • 2 = –4
–3 • 2 = –6
–4 • 2 = –8
–5 • 2 = –10

178. 5 • 2 = 10
4•2= 8
3•2= 6
2•2= 4
1•2= 2
0•2= 0
–1 • 2 = –2
–2 • 2 = –4
–3 • 2 = –6
–4 • 2 = –8
–5 • 2 = –10

179. 5 • 2 = 10
What can you say about 4•2= 8
the product of a
negative number and a 3•2= 6
positive number?
2•2= 4
1•2= 2
0•2= 0
–1 • 2 = –2
–2 • 2 = –4
–3 • 2 = –6
–4 • 2 = –8
–5 • 2 = –10

180. 5 • 2 = 10
What can you say about 4•2= 8
the product of a
negative number and a 3•2= 6
positive number?
2•2= 4
1•2= 2
0•2= 0
–1 • 2 = –2
–2 • 2 = –4
–3 • 2 = –6
–4 • 2 = –8
–5 • 2 = –10

181. 5 • 2 = 10
What can you say about 4•2= 8
the product of a
negative number and a 3•2= 6
positive number?
2•2= 4
1•2= 2
0•2= 0
–1 • 2 = –2
The product of a
–2 • 2 = –4
negative number and a
positive number is a
–3 • 2 = –6
negative number.
–4 • 2 = –8
–5 • 2 = –10

182. 5 • – 2 = –10
4•–2= –8
3•–2= –6
2•–2= –4
1 • – 2 = –2
0•–2= 0
–1 • – 2 = 2
–2 • – 2 = 4
–3 • – 2 = 6
–4 • – 2 = 8
–5 • – 2 = 10

183. 5 • – 2 = –10
4•–2= –8
3•–2= –6
2•–2= –4
1 • – 2 = –2
0•–2= 0
–1 • – 2 = 2
–2 • – 2 = 4
–3 • – 2 = 6
–4 • – 2 = 8
–5 • – 2 = 10

184. 5 • – 2 = –10
4•–2= –8
3•–2= –6
2•–2= –4
1 • – 2 = –2
0•–2= 0
–1 • – 2 = 2
–2 • – 2 = 4
–3 • – 2 = 6
–4 • – 2 = 8
–5 • – 2 = 10

185. 5 • – 2 = –10
4•–2= –8
3•–2= –6
2•–2= –4
1 • – 2 = –2
0•–2= 0
–1 • – 2 = 2
–2 • – 2 = 4
–3 • – 2 = 6
–4 • – 2 = 8
–5 • – 2 = 10

186. 5 • – 2 = –10
4•–2= –8
3•–2= –6
2•–2= –4
1 • – 2 = –2
0•–2= 0
–1 • – 2 = 2
–2 • – 2 = 4
–3 • – 2 = 6
–4 • – 2 = 8
–5 • – 2 = 10

187. 5 • – 2 = –10
4•–2= –8
3•–2= –6
2•–2= –4
1 • – 2 = –2
0•–2= 0
–1 • – 2 = 2
–2 • – 2 = 4
–3 • – 2 = 6
–4 • – 2 = 8
–5 • – 2 = 10

188. 5 • – 2 = –10
4•–2= –8
3•–2= –6
2•–2= –4
1 • – 2 = –2
0•–2= 0
–1 • – 2 = 2
–2 • – 2 = 4
–3 • – 2 = 6
–4 • – 2 = 8
–5 • – 2 = 10

189. 5 • – 2 = –10
4•–2= –8
3•–2= –6
2•–2= –4
1 • – 2 = –2
0•–2= 0
–1 • – 2 = 2
–2 • – 2 = 4
–3 • – 2 = 6
–4 • – 2 = 8
–5 • – 2 = 10

190. 5 • – 2 = –10
4•–2= –8
3•–2= –6
2•–2= –4
1 • – 2 = –2
0•–2= 0
–1 • – 2 = 2
–2 • – 2 = 4
–3 • – 2 = 6
–4 • – 2 = 8
–5 • – 2 = 10

191. 5 • – 2 = –10
4•–2= –8
3•–2= –6
2•–2= –4
1 • – 2 = –2
0•–2= 0
–1 • – 2 = 2
–2 • – 2 = 4
–3 • – 2 = 6
–4 • – 2 = 8
–5 • – 2 = 10

192. 5 • – 2 = –10
4•–2= –8
3•–2= –6
2•–2= –4
1 • – 2 = –2
0•–2= 0
–1 • – 2 = 2
–2 • – 2 = 4
–3 • – 2 = 6
–4 • – 2 = 8
–5 • – 2 = 10

193. 5 • – 2 = –10
4•–2= –8
3•–2= –6
2•–2= –4
1 • – 2 = –2
0•–2= 0
–1 • – 2 = 2
–2 • – 2 = 4
–3 • – 2 = 6
–4 • – 2 = 8
–5 • – 2 = 10

194. 5 • – 2 = –10
4•–2= –8
3•–2= –6
2•–2= –4
1 • – 2 = –2
0•–2= 0
–1 • – 2 = 2
–2 • – 2 = 4
–3 • – 2 = 6
–4 • – 2 = 8
–5 • – 2 = 10

195. 5 • – 2 = –10
4•–2= –8
3•–2= –6
2•–2= –4
1 • – 2 = –2
0•–2= 0
–1 • – 2 = 2
–2 • – 2 = 4
–3 • – 2 = 6
–4 • – 2 = 8
–5 • – 2 = 10

196. 5 • – 2 = –10
4•–2= –8
3•–2= –6
2•–2= –4
1 • – 2 = –2
0•–2= 0
–1 • – 2 = 2
–2 • – 2 = 4
–3 • – 2 = 6
–4 • – 2 = 8
–5 • – 2 = 10

197. 5 • – 2 = –10
4•–2= –8
3•–2= –6
2•–2= –4
1 • – 2 = –2
0•–2= 0
–1 • – 2 = 2
–2 • – 2 = 4
–3 • – 2 = 6
–4 • – 2 = 8
–5 • – 2 = 10

198. 5 • – 2 = –10
4•–2= –8
3•–2= –6
2•–2= –4
1 • – 2 = –2
0•–2= 0
–1 • – 2 = 2
–2 • – 2 = 4
–3 • – 2 = 6
–4 • – 2 = 8
–5 • – 2 = 10

199. From previous lesson the
product of a negative
5 • – 2 = –10
number and a positive 4•–2= –8
number is a negative
number. 3•–2= –6
2•–2= –4
1 • – 2 = –2
0•–2= 0
–1 • – 2 = 2
–2 • – 2 = 4
–3 • – 2 = 6
–4 • – 2 = 8
–5 • – 2 = 10

200. From previous lesson the
product of a negative
5 • – 2 = –10
number and a positive 4•–2= –8
number is a negative
number. 3•–2= –6
2•–2= –4
1 • – 2 = –2
What can you say about
the product of two
0•–2= 0
negative numbers? –1 • – 2 = 2
–2 • – 2 = 4
–3 • – 2 = 6
–4 • – 2 = 8
–5 • – 2 = 10

201. From previous lesson the
product of a negative
5 • – 2 = –10
number and a positive 4•–2= –8
number is a negative
number. 3•–2= –6
2•–2= –4
1 • – 2 = –2
What can you say about
the product of two
0•–2= 0
negative numbers? –1 • – 2 = 2
–2 • – 2 = 4
–3 • – 2 = 6
–4 • – 2 = 8
–5 • – 2 = 10

202. From previous lesson the
product of a negative
5 • – 2 = –10
number and a positive 4•–2= –8
number is a negative
number. 3•–2= –6
2•–2= –4
1 • – 2 = –2
What can you say about
the product of two
0•–2= 0
negative numbers? –1 • – 2 = 2
–2 • – 2 = 4
The product of two –3 • – 2 = 6
negative numbers is a
positive number. –4 • – 2 = 8
–5 • – 2 = 10

203. Expressions and
Equations
Philip Gonsalves

204. Expressions vs Equations

205. Expressions vs Equations
We simplify expressions

206. Expressions vs Equations
We simplify expressions
We solve equations

207. Expressions

208. Expressions
Simplify (evaluate) the expression:

209. Expressions
Simplify (evaluate) the expression:
2x + 4 when x=3

210. Expressions
Simplify (evaluate) the expression:
2x + 4 when x=3
2x + 4

211. Expressions
Simplify (evaluate) the expression:
2x + 4 when x=3
2x + 4

212. Expressions
Simplify (evaluate) the expression:
2x + 4 when x=3
2x + 4
= 2(3) + 4

213. Expressions
Simplify (evaluate) the expression:
2x + 4 when x=3
2x + 4
= 2(3) + 4
=6+4

214. Expressions
Simplify (evaluate) the expression:
2x + 4 when x=3
2x + 4
= 2(3) + 4
=6+4
= 10

215. Expressions
Simplify (evaluate) the expression:
2x + 4 when x=3
2x + 4
= 2(3) + 4
=6+4
= 10

216. Expressions
Simplify (evaluate) the expression:
2x + 4 when x=3
2x + 4 x + x + 4
= 2(3) + 4
=6+4
= 10

217. Expressions
Simplify (evaluate) the expression:
2x + 4 when x=3
2x + 4 x + x + 4
= 2(3) + 4 = 3 + 3 + 4
=6+4
= 10

218. Expressions
Simplify (evaluate) the expression:
2x + 4 when x=3
2x + 4 x + x + 4
= 2(3) + 4 = 3 + 3 + 4
=6+4 =6+4
= 10

219. Expressions
Simplify (evaluate) the expression:
2x + 4 when x=3
2x + 4 x + x + 4
= 2(3) + 4 = 3 + 3 + 4
=6+4 =6+4
= 10 = 10

220. Expressions
Simplify (evaluate) the expression:
2x + 4 when x=3
2x + 4 x + x + 4
= 2(3) + 4 = 3 + 3 + 4
=6+4 =6+4
= 10 = 10

221. Expressions
Simplify (evaluate) the expression:
2x + 4 when x=3
2x + 4 x + x + 4
x
= 2(3) + 4 = 3 + 3 + 4
=6+4 =6+4
= 10 = 10

222. Expressions
Simplify (evaluate) the expression:
2x + 4 when x=3
2x + 4 x + x + 4
x
= 2(3) + 4 = 3 + 3 + 4
x
=6+4 =6+4
= 10 = 10

223. Expressions
Simplify (evaluate) the expression:
2x + 4 when x=3
2x + 4 x + x + 4
x
= 2(3) + 4 = 3 + 3 + 4
x
=6+4 =6+4
= 10 = 10 1 1 1 1

224. Expressions
Simplify (evaluate) the expression:
2x + 4 when x=3
2x + 4 x + x + 4
1 1 1
= 2(3) + 4 = 3 + 3 + 4
x
=6+4 =6+4
= 10 = 10 1 1 1 1

225. Expressions
Simplify (evaluate) the expression:
2x + 4 when x=3
2x + 4 x + x + 4
1 1 1
= 2(3) + 4 = 3 + 3 + 4
1 1 1
=6+4 =6+4
= 10 = 10 1 1 1 1

226. Virtual Manipulatives:

229. x + 5 = 7

230. x + 5 = 7
x

231. x + 5 = 7
x 1 1
1 1
1

232. x + 5 = 7
x 1 1 1 1
1 1 1 1
1 1 1
1

233. x + 5 = 7
x 1 1 1 1
1 1 1 1
1 1 1
1

234. x + 5 = 7
x 1 1 1 1
1 1 1 1
1 1 1
1

235. x + 5 = 7
x 1 1 1 1
1 1 1 1
1 1 1
1

236. x + 5 = 7
x 1 1 1 1
1 1 1 1
1 1 1
1

237. x + 5 = 7
x 1 1 1 1
1 1 1 1
1 1 1
1

238. Solving Equations Side-by-side Comparison
x+5=7

239. Solving Equations Side-by-side Comparison
Traditional:
x+5=7

240. Solving Equations Side-by-side Comparison
Traditional:
x+5=7
−5 −5

241. Solving Equations Side-by-side Comparison
Traditional:
x+5=7
−5 −5

242. Solving Equations Side-by-side Comparison
Traditional:
x+5=7
−5 −5
x=2

243. Solving Equations Side-by-side Comparison
Traditional:
x+5=7
−5 −5
x=2

244. Solving Equations Side-by-side Comparison
Traditional:
x+5=7
−5 −5
x=2

245. Solving Equations Side-by-side Comparison
Traditional: Traditional:
Proper Syntax
x+5=7
−5 −5
x=2

246. Solving Equations Side-by-side Comparison
Traditional: Traditional:
Proper Syntax
x+5=7 x+5=7
−5 −5
x=2

247. Solving Equations Side-by-side Comparison
Traditional: Traditional:
Proper Syntax
x+5=7 x+5=7
−5 −5 x+5−5= 7−5
x=2

248. Solving Equations Side-by-side Comparison
Traditional: Traditional:
Proper Syntax
x+5=7 x+5=7
−5 −5 x+5−5= 7−5
x=2 x=2

249. Solving Equations Side-by-side Comparison
Traditional: Traditional:
Proper Syntax
x+5=7 x+5=7
−5 −5 x+5−5= 7−5
x=2 x=2

250. Solving Equations Side-by-side Comparison
Traditional: Traditional: Decomposition:
Proper Syntax
x+5=7 x+5=7
−5 −5 x+5−5= 7−5
x=2 x=2

251. Solving Equations Side-by-side Comparison
Traditional: Traditional: Decomposition:
Proper Syntax
x+5=7 x+5=7 x+5=7
−5 −5 x+5−5= 7−5
x=2 x=2

252. Solving Equations Side-by-side Comparison
Traditional: Traditional: Decomposition:
Proper Syntax
x+5=7 x+5=7 x+5=7
−5 −5 x+5−5= 7−5 x+5=5+2
x=2 x=2

253. Solving Equations Side-by-side Comparison
Traditional: Traditional: Decomposition:
Proper Syntax
x+5=7 x+5=7 x+5=7
−5 −5 x+5−5= 7−5 x+5=5+2
x=2 x=2

254. Solving Equations Side-by-side Comparison
Traditional: Traditional: Decomposition:
Proper Syntax
x+5=7 x+5=7 x+5=7
−5 −5 x+5−5= 7−5 x+5=5+2
x=2 x=2 x=2

255. Solving Equations Side-by-side Comparison
Traditional: Traditional: Decomposition:
Proper Syntax
x+5=7 x+5=7 x+5=7
−5 −5 x+5−5= 7−5 x+5=5+2
x=2 x=2 x=2

256. Solving Equations Side-by-side Comparison
Traditional: Traditional: Decomposition:
Proper Syntax
x+5=7 x+5=7 x+5=7
−5 −5 x+5−5= 7−5 x+5=5+2
x=2 x=2 x=2
Bar Model:

257. Solving Equations Side-by-side Comparison
Traditional: Traditional: Decomposition:
Proper Syntax
x+5=7 x+5=7 x+5=7
−5 −5 x+5−5= 7−5 x+5=5+2
x=2 x=2 x=2
Bar Model:
x

258. Solving Equations Side-by-side Comparison
Traditional: Traditional: Decomposition:
Proper Syntax
x+5=7 x+5=7 x+5=7
−5 −5 x+5−5= 7−5 x+5=5+2
x=2 x=2 x=2
Bar Model:
x 5

259. Solving Equations Side-by-side Comparison
Traditional: Traditional: Decomposition:
Proper Syntax
x+5=7 x+5=7 x+5=7
−5 −5 x+5−5= 7−5 x+5=5+2
x=2 x=2 x=2
Bar Model:
x 5
7

260. 57 + 38 = 56 + 39

261. 57 + 38 = 56 + 39
True or False?

262. 57 + 38 = 56 + 39
True or False?
How do you know?

263. 57 + 38 = 56 + 39
True or False?
How do you know?
57 + 38 = 56 + 39

264. 57 + 38 = 56 + 39
True or False?
How do you know?
57 + 38 = 56 + 39
95 = 95

265. 57 + 38 = 56 + 39
True or False?
How do you know?
57 + 38 = 56 + 39

266. 57 + 38 = 56 + 39
True or False?
How do you know?
57 + 38 = 56 + 39
(56 + 1) + 38

267. 57 + 38 = 56 + 39
True or False?
How do you know?
57 + 38 = 56 + 39
(56 + 1) + 38 = 56 + (1 + 38)

269. 573 + 368 = 571 + 364 + n

270. 573 + 368 = 571 + 364 + n
941 = 935 + n

271. 573 + 368 = 571 + 364 + n
941 = 935 + n
941 – 935 = 935 + n – 935

272. 573 + 368 = 571 + 364 + n
941 = 935 + n
941 – 935 = 935 + n – 935
6=n

273. Many ways to solve an equation
573 + 368 = 571 + 364 + n

274. Many ways to solve an equation
573 + 368 = 571 + 364 + n

275. Many ways to solve an equation
573 + 368 = 571 + 364 + n
571 + 2

276. Many ways to solve an equation
573 + 368 = 571 + 364 + n
571 + 2

277. Many ways to solve an equation
573 + 368 = 571 + 364 + n
571 + 2 + 364 + 4

278. Many ways to solve an equation
573 + 368 = 571 + 364 + n
571 + 2 + 364 + 4 = 571 + 364 + n

279. Many ways to solve an equation
573 + 368 = 571 + 364 + n
571 + 2 + 364 + 4 = 571 + 364 + n

280. Many ways to solve an equation
573 + 368 = 571 + 364 + n
571 + 2 + 364 + 4 = 571 + 364 + n

281. Many ways to solve an equation
573 + 368 = 571 + 364 + n
571 + 2 + 364 + 4 = 571 + 364 + n
2+4 =n

282. Many ways to solve an equation
573 + 368 = 571 + 364 + n
571 + 2 + 364 + 4 = 571 + 364 + n
2+4 =n
6=n

283. Solving Equations — Making
Connections to Prior Knowledge
573 + 368 = 571 + 364 + n

284. Solving Equations — Making
Connections to Prior Knowledge
573 + 368 = 571 + 364 + n
500 + 70 + 3

285. Solving Equations — Making
Connections to Prior Knowledge
573 + 368 = 571 + 364 + n
500 + 70 + 3 + 300 + 60 + 8

286. Solving Equations — Making
Connections to Prior Knowledge
573 + 368 = 571 + 364 + n
500 + 70 + 3 + 300 + 60 + 8 = 500 + 70 + 1

287. Solving Equations — Making
Connections to Prior Knowledge
573 + 368 = 571 + 364 + n
500 + 70 + 3 + 300 + 60 + 8 = 500 + 70 + 1 + 300 + 60 + 4 + n

288. Solving Equations — Making
Connections to Prior Knowledge
573 + 368 = 571 + 364 + n
500 + 70 + 3 + 300 + 60 + 8 = 500 + 70 + 1 + 300 + 60 + 4 + n

289. Solving Equations — Making
Connections to Prior Knowledge
573 + 368 = 571 + 364 + n
500 + 70 + 3 + 300 + 60 + 8 = 500 + 70 + 1 + 300 + 60 + 4 + n

290. Solving Equations — Making
Connections to Prior Knowledge
573 + 368 = 571 + 364 + n
500 + 70 + 3 + 300 + 60 + 8 = 500 + 70 + 1 + 300 + 60 + 4 + n

291. Solving Equations — Making
Connections to Prior Knowledge
573 + 368 = 571 + 364 + n
500 + 70 + 3 + 300 + 60 + 8 = 500 + 70 + 1 + 300 + 60 + 4 + n

292. Solving Equations — Making
Connections to Prior Knowledge
573 + 368 = 571 + 364 + n
500 + 70 + 3 + 300 + 60 + 8 = 500 + 70 + 1 + 300 + 60 + 4 + n
3+ 8 = 1+ 4 + n

293. Solving Equations — Making
Connections to Prior Knowledge
573 + 368 = 571 + 364 + n
500 + 70 + 3 + 300 + 60 + 8 = 500 + 70 + 1 + 300 + 60 + 4 + n
3+ 8 = 1+ 4 + n
11 = 5 + n

294. Solving Equations — Making
Connections to Prior Knowledge
573 + 368 = 571 + 364 + n
500 + 70 + 3 + 300 + 60 + 8 = 500 + 70 + 1 + 300 + 60 + 4 + n
3+ 8 = 1+ 4 + n
11 = 5 + n

295. Solving Equations — Making
Connections to Prior Knowledge
573 + 368 = 571 + 364 + n
500 + 70 + 3 + 300 + 60 + 8 = 500 + 70 + 1 + 300 + 60 + 4 + n
3+ 8 = 1+ 4 + n
11 = 5 + n
5+6=5+n

296. Solving Equations — Making
Connections to Prior Knowledge
573 + 368 = 571 + 364 + n
500 + 70 + 3 + 300 + 60 + 8 = 500 + 70 + 1 + 300 + 60 + 4 + n
3+ 8 = 1+ 4 + n
11 = 5 + n
5+6=5+n

297. Solving Equations — Making
Connections to Prior Knowledge
573 + 368 = 571 + 364 + n
500 + 70 + 3 + 300 + 60 + 8 = 500 + 70 + 1 + 300 + 60 + 4 + n
3+ 8 = 1+ 4 + n
11 = 5 + n
5+6=5+n
6=n

298. Solving Equations — Making
Connections to Prior Knowledge
573 + 368 = 571 + 364 + n
500 + 70 + 3 + 300 + 60 + 8 = 500 + 70 + 1 + 300 + 60 + 4 + n
3+ 8 = 1+ 4 + n
11 = 5 + n
5+6=5+n
6=n
Focus: Relationships & Balance

299. Solving Equations — Making
Connections to Prior Knowledge
573 + 368 = 571 + 364 + n
500 + 70 + 3 + 300 + 60 + 8 = 500 + 70 + 1 + 300 + 60 + 4 + n
3+ 8 = 1+ 4 + n
11 = 5 + n
5+6=5+n
6=n
Focus: Relationships & Balance
Connect to prior knowledge: Expanded Notation

300. “Canceling”

301. “Canceling”
• Doesn’t exist

302. “Canceling”
• Doesn’t exist
• We are either looking for ones or zeros
depending on if we are multiplying/
dividing or adding/subtracting

303. “Canceling”
• Doesn’t exist
• We are either looking for ones or zeros
depending on if we are multiplying/
dividing or adding/subtracting
• Such terms can create problems - it is
easier for students to “cancel” things
and get rid of them than to deal with
them

304. “Canceling” — Looking for 1’s

305. “Canceling” — Looking for 1’s
2x
2

306. “Canceling” — Looking for 1’s
2x 2• x
=
2 2 •1

307. “Canceling” — Looking for 1’s
2x
2 1
=
2• x
2 •1

308. “Canceling” — Looking for 1’s
2x
2 1
=
=
2• x
2 •1
x
1

309. “Canceling” — Looking for 1’s
2x
2 1
=
=
2• x
2 •1
x
1
=x

310. “Canceling” — Looking for 1’s
2x
2 1
=
=
2• x
2 •1
x
VS
1
=x

311. “Canceling” — Looking for 1’s
2x
2 1
=
=
2• x
2 •1
x
VS
2x
2
1
=x

312. “Canceling” — Looking for 1’s
2x
2 1
=
=
2• x
2 •1
x
VS
2x
2
=x
1
=x

313. “Canceling” — Looking for 1’s
2x
2 1
=
=
2• x
2 •1
x
VS
2x
2
=x
1
=x

314. “Canceling” — Looking for 1’s
2x
2 1
=
=
2• x
2 •1
x
VS
2x
2
=x
1
=x

315. “Canceling” — Looking for 1’s
Common error from
1
“canceling”
2x 2• x VS
2x
=
2 2 •1 2
x =x
=
1
=x

316. “Canceling” — Looking for 1’s
Common error from
1
“canceling”
2x 2• x VS
2x
= 2+x
2 2 •1 2
2
x =x
=
1
=x

317. “Canceling” — Looking for 1’s
Common error from
1
“canceling”
2x 2• x VS
2x
= 2+x
2 2 •1 2
2
x =x
=
1
=x

318. “Canceling” — Looking for 1’s
Common error from
1
“canceling”
2x 2• x VS
2x
= 2+x
2 2 •1 2
2
x =x ≠x
=
1
=x

319. “Canceling” — Looking for 1’s
Common error from
1
“canceling”
2x 2• x VS
2x
= 2+x
2 2 •1 2
2
x =x ≠x
=
1
=x

320. “Canceling” — Looking for 1’s
Common error from
1
“canceling”
2x 2• x VS
2x
= 2+x
2 2 •1 2
2
x =x ≠x
=
1 2+x
=x 2

321. “Canceling” — Looking for 1’s
Common error from
1
“canceling”
2x 2• x VS
2x
= 2+x
2 2 •1 2
2
x =x ≠x
=
1 2+x 2 x
= +
=x 2 2 2

322. “Canceling” — Looking for 1’s
Common error from
1
“canceling”
2x 2• x VS
2x
= 2+x
2 2 •1 2
2
x =x ≠x
=
1
=x
2+x 2 x
2
= +
2 21

323. “Canceling” — Looking for 1’s
Common error from
1
“canceling”
2x 2• x VS
2x
= 2+x
2 2 •1 2
2
x =x ≠x
=
1
=x
2+x 2 x
2
= +
1
2 2
x
= 1 +
2

324. Looking for 0’s and 1’s

325. Looking for 0’s and 1’s
2x + 1 = 7

326. Looking for 0’s and 1’s
2x + 1 = 7
2x + 1 − 1 = 7 − 1

327. Looking for 0’s and 1’s
2x + 1 = 7
2x + 1 − 1 = 7 − 1

328. Looking for 0’s and 1’s
2x + 1 = 7
2x + 1 − 1 = 7 − 1
2x = 6

329. Looking for 0’s and 1’s
2x + 1 = 7
2x + 1 − 1 = 7 − 1
2x = 6
2x 6
=
2 2

330. Looking for 0’s and 1’s
2x + 1 = 7
2x + 1 − 1 = 7 − 1
2x = 6
12x 6
=
2 2

331. Looking for 0’s and 1’s
2x + 1 = 7
2x + 1 − 1 = 7 − 1
2x = 6
12x 6
=
2 2
x=3

332. Looking for 0’s and 1’s
2x + 1 = 7
2x + 1 − 1 = 7 − 1
2x = 6
12x 6
=
2 2
x=3

333. Looking for 0’s and 1’s
2x + 1 = 7 Check:
2x + 1 − 1 = 7 − 1
2x = 6
12x 6
=
2 2
x=3

334. Looking for 0’s and 1’s
2x + 1 = 7 Check: 2x + 1 = 7
2x + 1 − 1 = 7 − 1
2x = 6
12x 6
=
2 2
x=3

335. Looking for 0’s and 1’s
2x + 1 = 7 Check: 2x + 1 = 7
2x + 1 − 1 = 7 − 1
2x = 6
12x 6
=
2 2
x=3

336. Looking for 0’s and 1’s
2x + 1 = 7 Check: 2x + 1 = 7
2x + 1 − 1 = 7 − 1 2 ( 3) + 1
2x = 6
12x 6
=
2 2
x=3

337. Looking for 0’s and 1’s
2x + 1 = 7 Check: 2x + 1 = 7
2x + 1 − 1 = 7 − 1 2 ( 3) + 1
6 +1
2x = 6
12x 6
=
2 2
x=3

338. Looking for 0’s and 1’s
2x + 1 = 7 Check: 2x + 1 = 7
2x + 1 − 1 = 7 − 1 2 ( 3) + 1
6 +1
2x = 6
1
7
2x 6
=
2 2
x=3

339. Looking for 0’s and 1’s
2x + 1 = 7 Check: 2x + 1 = 7
2x + 1 − 1 = 7 − 1 2 ( 3) + 1
6 +1
2x = 6
1
7 7
2x 6
=
2 2
x=3

340. Solving Equations
2x + 1 = 7

341. Solving Equations
2x + 1 = 7

342. Solving Equations
2x + 1 = 7
x 1 1 1
x 1 1 1
1 1

343. Solving Equations
2x + 1 = 7
2x + 1 − 1 = 7 − 1
x 1 1 1
x 1 1 1
1 1

344. Solving Equations
2x + 1 = 7
2x + 1 − 1 = 7 − 1
x 1 1 1
x 1 1 1
1 1

345. Solving Equations
2x + 1 = 7
2x + 1 − 1 = 7 − 1
x 1 1 1
x 1 1 1

346. Solving Equations
2x + 1 = 7
2x + 1 − 1 = 7 − 1
2x = 6
x 1 1 1
x 1 1 1

347. Solving Equations
2x + 1 = 7
2x + 1 − 1 = 7 − 1
2x = 6
x 1 1 1
2x 6
= x 1 1 1
2 2

348. Solving Equations
2x + 1 = 7
2x + 1 − 1 = 7 − 1
2x = 6
1
x 1 1 1
2x 6
= x 1 1 1
2 2

349. Solving Equations
2x + 1 = 7
2x + 1 − 1 = 7 − 1
2x = 6
1
x 1 1 1
2x 6
= x 1 1 1
2 2
x=3

350. Solving Equations
2x + 1 = 7
2x + 1 − 1 = 7 − 1
2x = 6
1
x 1 1 1
2x 6
= x 1 1 1
2 2
x=3

351. 2x + 1 = 7
2x + 1 − 1 = 7 − 1
2x = 6
12x 6
=
2 2
x=3

352. Not the only way to solve ...
2x + 1 = 7
2x + 1 − 1 = 7 − 1
2x = 6
12x 6
=
2 2
x=3

353. Side-by-side Comparison
2x + 1 = 7
2x + 1 − 1 = 7 − 1
2x = 6
12x 6
=
2 2
x=3

354. Side-by-side Comparison
2x + 1 = 7
2x + 1 − 1 = 7 − 1
2x = 6
12x 6
=
2 2
x=3

355. Side-by-side Comparison
2x + 1 = 7 2x + 1 = 7
2x + 1 − 1 = 7 − 1
2x = 6
12x 6
=
2 2
x=3

356. Side-by-side Comparison
2x + 1 = 7 2x + 1 = 7
2x + 1 − 1 = 7 − 1 2x 1 7
+ =
2 2 2
2x = 6
12x 6
=
2 2
x=3

357. Side-by-side Comparison
2x + 1 = 7 2x + 1 = 7
2x + 1 − 1 = 7 − 1
2x = 6
1
2x 1 7
+ =
2 2 2
12x 6
=
2 2
x=3

358. Side-by-side Comparison
2x + 1 = 7 2x + 1 = 7
2x + 1 − 1 = 7 − 1
2x = 6
12x 1 7
+ =
2 2 2
1 1 7 1
1
x+ − = −
2x 6 2 2 2 2
=
2 2
x=3

359. Side-by-side Comparison
2x + 1 = 7 2x + 1 = 7
2x + 1 − 1 = 7 − 1
2x = 6
12x 1 7
+ =
2 2 2
1 1 7 1
1
x+ − = −
2x 6 2 2 2 2
=
2 2 6
x=
x=3 2

360. Side-by-side Comparison
2x + 1 = 7 2x + 1 = 7
2x + 1 − 1 = 7 − 1
2x = 6
12x 1 7
+ =
2 2 2
1 1 7 1
1
x+ − = −
2x 6 2 2 2 2
=
2 2 6
x=
x=3 2
x=3

361. 2x + 1 = 7
2x + 1 − 1 = 7 − 1
2x = 6
12x 6
=
2 2
x=3

362. Bar Models
2x + 1 = 7
2x + 1 − 1 = 7 − 1
2x = 6
12x 6
=
2 2
x=3

363. Bar Models
2x + 1 = 7
2x
2x + 1 − 1 = 7 − 1
2x = 6
12x 6
=
2 2
x=3

364. Bar Models
2x + 1 = 7
2x 1
2x + 1 − 1 = 7 − 1 7
2x = 6
12x 6
=
2 2
x=3

365. Bar Models
2x + 1 = 7
2x 1
2x + 1 − 1 = 7 − 1 7
2x = 6
2x 1
12x 6
=
2 2
x=3

366. Bar Models
2x + 1 = 7
2x 1
2x + 1 − 1 = 7 − 1 7
2x = 6
2x 1
12x 6
=
2 2
6 1
x=3

367. Bar Models
2x + 1 = 7
2x 1
2x + 1 − 1 = 7 − 1 7
2x = 6
2x 1
12x 6
=
2 2
x
6
x
1
1
x=3
3 3 1

368. Bar Models & Decomposition
2x + 1 = 7
2x 1
2x + 1 − 1 = 7 − 1 7
2x = 6
2x 1
12x 6
=
2 2
x
6
x
1
1
x=3
3 3 1

369. Relational Thinking
y
=5
4

370. Relational Thinking
y
=5
4

371. Relational Thinking
y
=5
4

372. Relational Thinking
5 5 5 5
y
=5
4

373. Relational Thinking
5 5 5 5
14 2 4 3
20
y
=5
4

374. Relational Thinking
5 5 5 5
14 2 4 3
20
y
=5
4
⎛ y ⎞
4 ⎜ ⎟ = 4 ( 5 )
⎝ 4 ⎠

375. Relational Thinking
5 5 5 5
14 2 4 3
20
y
=5
4
⎛ y ⎞
4 ⎜ ⎟ = 4 ( 5 )
⎝ 4 ⎠
y = 20

376. Relational Thinking
5 5 5 5
14 2 4 3
20
y
=5
4
⎛ y ⎞
4 ⎜ ⎟ = 4 ( 5 )
⎝ 4 ⎠
y = 20

377. Relational Thinking
5 5 5 5
14 2 4 3
20
y y
=5 =5
4 4
⎛ y ⎞
4 ⎜ ⎟ = 4 ( 5 )
⎝ 4 ⎠
y = 20

378. Relational Thinking
5 5 5 5
14 2 4 3
20
y y
=5 =5
4 4
⎛ y ⎞ y y y y
4 ⎜ ⎟ = 4 ( 5 ) + + + =5+5+5+5
⎝ 4 ⎠ 4 4 4 4
y = 20

379. Relational Thinking
5 5 5 5
14 2 4 3
20
y y
=5 =5
4 4
⎛ y ⎞ y y y y
4 ⎜ ⎟ = 4 ( 5 ) + + + =5+5+5+5
⎝ 4 ⎠ 4 4 4 4
y = 20 y = 20

381. 2x
=8
3

382. 2x
=8
3

383. 2x
=8
3

384. {
2x
8 =8
3

385. 4 4
{
2x
8 =8
3

386. 4 4 4
{
2x
8 =8
3

387. 4 4 4
{
2x
8 =8
3
1 1
x+ x=4+4
3 3

388. 4 4 4
{
2x
8 =8
3
1 1
x+ x=4+4
3 3

389. 4 4 4
{
2x
8 =8
3
1 1
x+ x=4+4
3 3
1 1 1
x+ x+ x=4+4+4
3 3 3

390. 4 4 4
{
2x
8 =8
3
1 1
x+ x=4+4
3 3
1 1 1
x+ x+ x=4+4+4
3 3 3
x = 12

391. 4 4 4
{
2x
8 =8
3
1 1
x+ x=4+4
3 3
1 1 1
x+ x+ x=4+4+4
3 3 3
x = 12

392. 4 4 4
{
2x 2x
8 =8 =8
3 3
1 1
x+ x=4+4
3 3
1 1 1
x+ x+ x=4+4+4
3 3 3
x = 12

393. 4 4 4
{
2x 2x
8 =8 =8
3 3
1 1 3 ⎛ 2x ⎞ 3
x+ x=4+4 ⎜ ⎟ = ( 8 )
3 3 2 ⎝ 3 ⎠ 2
1 1 1
x+ x+ x=4+4+4
3 3 3
x = 12

394. 4 4 4
{
2x 2x
8 =8 =8
3 3
1 1 3 ⎛ 2x ⎞ 3
x+ x=4+4 ⎜ ⎟ = ( 8 )
3 3 2 ⎝ 3 ⎠ 2
1 1 1
x+ x+ x=4+4+4 x = 12
3 3 3
x = 12

395. Building Flexibility

396. Building Flexibility
3( x + 1) = 15

397. Building Flexibility
3( x + 1) = 15
3x + 3 = 15

398. Building Flexibility
3( x + 1) = 15
3x + 3 = 15
3x + 3 − 3 = 15 − 3

399. Building Flexibility
3( x + 1) = 15
3x + 3 = 15
3x + 3 − 3 = 15 − 3
3x = 12

400. Building Flexibility
3( x + 1) = 15
3x + 3 = 15
3x + 3 − 3 = 15 − 3
3x = 12
3x 12
=
3 3

401. Building Flexibility
3( x + 1) = 15
3x + 3 = 15
3x + 3 − 3 = 15 − 3
3x = 12
3x 12
=
3 3

402. Building Flexibility
3( x + 1) = 15
3x + 3 = 15
3x + 3 − 3 = 15 − 3
3x = 12
3x 12
=
3 3
x=4

403. Building Flexibility
3( x + 1) = 15
3x + 3 = 15
3x + 3 − 3 = 15 − 3
3x = 12
3x 12
=
3 3
x=4

404. Building Flexibility
3( x + 1) = 15 3( x + 1) = 15
3x + 3 = 15
3x + 3 − 3 = 15 − 3
3x = 12
3x 12
=
3 3
x=4

405. Building Flexibility
3( x + 1) = 15 3( x + 1) = 15
3x + 3 = 15 3( x + 1) 15
=
3x + 3 − 3 = 15 − 3 3 3
3x = 12
3x 12
=
3 3
x=4

406. Building Flexibility
3( x + 1) = 15 3( x + 1) = 15
3x + 3 = 15 3( x + 1) 15
=
3x + 3 − 3 = 15 − 3 3 3
3x = 12
3x 12
=
3 3
x=4

407. Building Flexibility
3( x + 1) = 15 3( x + 1) = 15
3x + 3 = 15 3( x + 1) 15
=
3x + 3 − 3 = 15 − 3 3 3
3x = 12 x +1= 5
3x 12
=
3 3
x=4

408. Building Flexibility
3( x + 1) = 15 3( x + 1) = 15
3x + 3 = 15 3( x + 1) 15
=
3x + 3 − 3 = 15 − 3 3 3
3x = 12 x +1= 5
3x 12 x +1−1 = 5 −1
=
3 3
x=4

409. Building Flexibility
3( x + 1) = 15 3( x + 1) = 15
3x + 3 = 15 3( x + 1) 15
=
3x + 3 − 3 = 15 − 3 3 3
3x = 12 x +1= 5
3x 12 x +1−1 = 5 −1
=
3 3
x=4
x=4

410. 3( x + 1) = 15
3( x + 1) 15
=
3 3
x +1= 5
x +1−1 = 5 −1
x=4

411. 3( x + 1) = 15
3( x + 1) 15
=
3 3
x +1= 5
x +1−1 = 5 −1
x=4

412. 3( x + 1) = 15
3( x + 1) 15
=
3 3
1 42 43
x +1= 5
15
x +1−1 = 5 −1
x=4

413. 3( x + 1) = 15
3( x + 1) 15
=
3 3
1 42 43
x +1= 5
15
x +1−1 = 5 −1
x=4

414. 3( x + 1) = 15
3( x + 1) 15
=
3 3
1 42 43
x+1 x+1 x+1
x +1= 5
15
x +1−1 = 5 −1
x=4

415. 3( x + 1) = 15
} } }
5 5 5
3( x + 1) 15
=
3 3
1 42 43
x+1 x+1 x+1
x +1= 5
15
x +1−1 = 5 −1
x=4

416. Building Intuition

417. Building Intuition
3( x + 1) = 14

418. Building Intuition
3( x + 1) = 14
3x + 3 = 14

419. Building Intuition
3( x + 1) = 14
3x + 3 = 14
3x + 3 − 3 = 14 − 3

420. Building Intuition
3( x + 1) = 14
3x + 3 = 14
3x + 3 − 3 = 14 − 3
3x = 11

421. Building Intuition
3( x + 1) = 14
3x + 3 = 14
3x + 3 − 3 = 14 − 3
3x = 11
3x 11
=
3 3

422. Building Intuition
3( x + 1) = 14
3x + 3 = 14
3x + 3 − 3 = 14 − 3
3x = 11
3x 11
=
3 3

423. Building Intuition
3( x + 1) = 14
3x + 3 = 14
3x + 3 − 3 = 14 − 3
3x = 11
3x 11
=
3 3
11
x=
3

424. Building Intuition
3( x + 1) = 14
3x + 3 = 14
3x + 3 − 3 = 14 − 3
3x = 11
3x 11
=
3 3
11
x=
3

425. Building Intuition
3( x + 1) = 14 3( x + 1) = 14
3x + 3 = 14
3x + 3 − 3 = 14 − 3
3x = 11
3x 11
=
3 3
11
x=
3

426. Building Intuition
3( x + 1) = 14 3( x + 1) = 14
3x + 3 = 14 3( x + 1) 14
=
3x + 3 − 3 = 14 − 3 3 3
3x = 11
3x 11
=
3 3
11
x=
3

427. Building Intuition
3( x + 1) = 14 3( x + 1) = 14
3x + 3 = 14 3( x + 1) 14
=
3x + 3 − 3 = 14 − 3 3 3
3x = 11
3x 11
=
3 3
11
x=
3

428. Building Intuition
3( x + 1) = 14 3( x + 1) = 14
3x + 3 = 14 3( x + 1) 14
=
3x + 3 − 3 = 14 − 3 3 3
14
3x = 11 x +1=
3
3x 11
=
3 3
11
x=
3

429. Building Intuition
3( x + 1) = 14 3( x + 1) = 14
3x + 3 = 14 3( x + 1) 14
=
3x + 3 − 3 = 14 − 3 3 3
14
3x = 11 x +1=
3
3x 11 14 3
= x +1−1 = −
3 3 3 3
11
x=
3

430. Building Intuition
3( x + 1) = 14 3( x + 1) = 14
3x + 3 = 14 3( x + 1) 14
=
3x + 3 − 3 = 14 − 3 3 3
14
3x = 11 x +1=
3
3x 11 14 3
= x +1−1 = −
3 3 3 3
11 11
x= x=
3 3

431. Fractional Equations

433. 1 1 1
x + =
2 4 3

434. 1 1 1
x + =
2 4 3
1 1 1 1 1
x + − = −
2 4 4 3 4

435. 1 1 1
x + =
2 4 3
1 1 1 1 1
x + − = −
2 4 4 3 4
1 1
x =
2 12

436. 1 1 1
x + =
2 4 3
1 1
1 1 1 1 1 −
x + − = − 3 4
2 4 4 3 4 4 3
= −
1 1 12 12
x = 1
2 12 =
12

437. 1 1 1
x + =
2 4 3
1 1
1 1 1 1 1 −
x + − = − 3 4
2 4 4 3 4 4 3
= −
1 1 12 12
x = 1
2 12 =
12
⎛ 1 ⎞ ⎛ 1 ⎞
2 ⎜ x ⎟ = 2 ⎜ ⎟
⎝ 2 ⎠ ⎝ 12 ⎠

438. 1 1 1
x + =
2 4 3
1 1
1 1 1 1 1 −
x + − = − 3 4
2 4 4 3 4 4 3
= −
1 1 12 12
x = 1
2 12 =
12
⎛ 1 ⎞ ⎛ 1 ⎞
2 ⎜ x ⎟ = 2 ⎜ ⎟
⎝ 2 ⎠ ⎝ 12 ⎠
1
x =
6

439. 1 1 1
x + =
2 4 3
1 1 1 1 1
x + − = −
2 4 4 3 4
1 1
x =
2 12
⎛ 1 ⎞ ⎛ 1 ⎞
2 ⎜ x ⎟ = 2 ⎜ ⎟
⎝ 2 ⎠ ⎝ 12 ⎠
1
x =
6

440. 1 1 1
x + =
2 4 3
1 1 1 1 1
x + − = −
2 4 4 3 4
1 1
x =
2 12
⎛ 1 ⎞ ⎛ 1 ⎞
2 ⎜ x ⎟ = 2 ⎜ ⎟
⎝ 2 ⎠ ⎝ 12 ⎠
1
x =
6

441. 1 1 1 1 1 1
x + = x + =
2 4 3 2 4 3
1 1 1 1 1
x + − = −
2 4 4 3 4
1 1
x =
2 12
⎛ 1 ⎞ ⎛ 1 ⎞
2 ⎜ x ⎟ = 2 ⎜ ⎟
⎝ 2 ⎠ ⎝ 12 ⎠
1
x =
6

442. 1 1 1 1 1 1
x + = x + =
2 4 3 2 4 3
1 1 1 1 1 ⎛ 1 ⎞ ⎛ 1 ⎞ ⎛ 1 ⎞
x + − = − 12 ⎜ x ⎟ + 12 ⎜ ⎟ = 12 ⎜ ⎟
2 4 4 3 4 ⎝ 2 ⎠ ⎝ 4 ⎠ ⎝ 3 ⎠
1 1
x =
2 12
⎛ 1 ⎞ ⎛ 1 ⎞
2 ⎜ x ⎟ = 2 ⎜ ⎟
⎝ 2 ⎠ ⎝ 12 ⎠
1
x =
6

443. 1 1 1 1 1 1
x + = x + =
2 4 3 2 4 3
1 1 1 1 1 ⎛ 1 ⎞ ⎛ 1 ⎞ ⎛ 1 ⎞
x + − = − 12 ⎜ x ⎟ + 12 ⎜ ⎟ = 12 ⎜ ⎟
2 4 4 3 4 ⎝ 2 ⎠ ⎝ 4 ⎠ ⎝ 3 ⎠
1 1 6x + 3 = 4
x =
2 12
⎛ 1 ⎞ ⎛ 1 ⎞
2 ⎜ x ⎟ = 2 ⎜ ⎟
⎝ 2 ⎠ ⎝ 12 ⎠
1
x =
6

444. 1 1 1 1 1 1
x + = x + =
2 4 3 2 4 3
1 1 1 1 1 ⎛ 1 ⎞ ⎛ 1 ⎞ ⎛ 1 ⎞
x + − = − 12 ⎜ x ⎟ + 12 ⎜ ⎟ = 12 ⎜ ⎟
2 4 4 3 4 ⎝ 2 ⎠ ⎝ 4 ⎠ ⎝ 3 ⎠
1 1 6x + 3 = 4
x =
2 12 6x + 3 − 3 = 4 − 3
⎛ 1 ⎞ ⎛ 1 ⎞
2 ⎜ x ⎟ = 2 ⎜ ⎟
⎝ 2 ⎠ ⎝ 12 ⎠
1
x =
6

445. 1 1 1 1 1 1
x + = x + =
2 4 3 2 4 3
1 1 1 1 1 ⎛ 1 ⎞ ⎛ 1 ⎞ ⎛ 1 ⎞
x + − = − 12 ⎜ x ⎟ + 12 ⎜ ⎟ = 12 ⎜ ⎟
2 4 4 3 4 ⎝ 2 ⎠ ⎝ 4 ⎠ ⎝ 3 ⎠
1 1 6x + 3 = 4
x =
2 12 6x + 3 − 3 = 4 − 3
⎛ 1 ⎞ ⎛ 1 ⎞ 6x = 1
2 ⎜ x ⎟ = 2 ⎜ ⎟
⎝ 2 ⎠ ⎝ 12 ⎠
1
x =
6

446. 1 1 1 1 1 1
x + = x + =
2 4 3 2 4 3
1 1 1 1 1 ⎛ 1 ⎞ ⎛ 1 ⎞ ⎛ 1 ⎞
x + − = − 12 ⎜ x ⎟ + 12 ⎜ ⎟ = 12 ⎜ ⎟
2 4 4 3 4 ⎝ 2 ⎠ ⎝ 4 ⎠ ⎝ 3 ⎠
1 1 6x + 3 = 4
x =
2 12 6x + 3 − 3 = 4 − 3
⎛ 1 ⎞ ⎛ 1 ⎞ 6x = 1
2 ⎜ x ⎟ = 2 ⎜ ⎟
⎝ 2 ⎠ ⎝ 12 ⎠ 6 1
x=
1 6 6
x =
6

447. 1 1 1 1 1 1
x + = x + =
2 4 3 2 4 3
1 1 1 1 1 ⎛ 1 ⎞ ⎛ 1 ⎞ ⎛ 1 ⎞
x + − = − 12 ⎜ x ⎟ + 12 ⎜ ⎟ = 12 ⎜ ⎟
2 4 4 3 4 ⎝ 2 ⎠ ⎝ 4 ⎠ ⎝ 3 ⎠
1 1 6x + 3 = 4
x =
2 12 6x + 3 − 3 = 4 − 3
⎛ 1 ⎞ ⎛ 1 ⎞ 6x = 1
2 ⎜ x ⎟ = 2 ⎜ ⎟
⎝ 2 ⎠
x =
1
6
⎝ 12 ⎠
1 6
6
x=
1
6

448. 1 1 1 1 1 1
x + = x + =
2 4 3 2 4 3
1 1 1 1 1 ⎛ 1 ⎞ ⎛ 1 ⎞ ⎛ 1 ⎞
x + − = − 12 ⎜ x ⎟ + 12 ⎜ ⎟ = 12 ⎜ ⎟
2 4 4 3 4 ⎝ 2 ⎠ ⎝ 4 ⎠ ⎝ 3 ⎠
1 1 6x + 3 = 4
x =
2 12 6x + 3 − 3 = 4 − 3
⎛ 1 ⎞ ⎛ 1 ⎞ 6x = 1
2 ⎜ x ⎟ = 2 ⎜ ⎟
⎝ 2 ⎠
x =
1
6
⎝ 12 ⎠
1 6
6
x=
x =
1
6
1
6

449. Decimal Equations

451. 1 1 1
x + =
2 5 4

452. 1 1 1
x + =
2 5 4
0.50x + 0.20 = 0.25

453. 1 1 1
x + =
2 5 4
0.50x + 0.20 = 0.25
100 ( 0.50x ) + 100 ( 0.20 ) = 100 (.25 )

454. 1 1 1
x + =
2 5 4
0.50x + 0.20 = 0.25
100 ( 0.50x ) + 100 ( 0.20 ) = 100 (.25 )
50x + 20 = 25

455. 1 1 1
x + =
2 5 4
0.50x + 0.20 = 0.25
100 ( 0.50x ) + 100 ( 0.20 ) = 100 (.25 )
50x + 20 = 25
50x + 20 − 20 = 25 − 20

456. 1 1 1
x + =
2 5 4
0.50x + 0.20 = 0.25
100 ( 0.50x ) + 100 ( 0.20 ) = 100 (.25 )
50x + 20 = 25
50x + 20 − 20 = 25 − 20
50x = 5

457. 1 1 1
x + =
2 5 4
0.50x + 0.20 = 0.25
100 ( 0.50x ) + 100 ( 0.20 ) = 100 (.25 )
50x + 20 = 25
50x + 20 − 20 = 25 − 20
50x = 5
50 5
x =
50 50

458. 1 1 1
x + =
2 5 4
0.50x + 0.20 = 0.25
100 ( 0.50x ) + 100 ( 0.20 ) = 100 (.25 )
50x + 20 = 25
50x + 20 − 20 = 25 − 20
50x = 5
50 5
x =
50 50
1
x =
10

459. What is the value of the circle?

460. What is the value of the circle?

461. What is the value of the circle?

462. What is the value of the circle?

463. What is the value of the circle?

464. What is the value of the circle?

465. Solving equations with variables on both sides...
3x = 2x + 20

466. Solving equations with variables on both sides...
3x = 2x + 20
Bar Model: Decomposition: Inverse operations:

467. Solving equations with variables on both sides...
3x = 2x + 20
Bar Model: Decomposition: Inverse operations:
3x
2x + 20

468. Solving equations with variables on both sides...
3x = 2x + 20
Bar Model: Decomposition: Inverse operations:
3x
2x + 20
x x x
x x 20

469. Solving equations with variables on both sides...
3x = 2x + 20
Bar Model: Decomposition: Inverse operations:
3x
2x + 20
x x x
x x 20
∴ x = 20

470. Solving equations with variables on both sides...
3x = 2x + 20
Bar Model: Decomposition: Inverse operations:
3x
2x + 20
x x x
x x 20
∴ x = 20

471. Solving equations with variables on both sides...
3x = 2x + 20
Bar Model: Decomposition: Inverse operations:
3x 3x = 2x + 20
2x + 20
x x x
x x 20
∴ x = 20

472. Solving equations with variables on both sides...
3x = 2x + 20
Bar Model: Decomposition: Inverse operations:
3x 3x = 2x + 20
2x + 20 x + x + x = x + x + 20
x x x
x x 20
∴ x = 20

473. Solving equations with variables on both sides...
3x = 2x + 20
Bar Model: Decomposition: Inverse operations:
3x 3x = 2x + 20
2x + 20 x + x + x = x + x + 20
x x x
x x 20
∴ x = 20

474. Solving equations with variables on both sides...
3x = 2x + 20
Bar Model: Decomposition: Inverse operations:
3x 3x = 2x + 20
2x + 20 x + x + x = x + x + 20
x x x
x x 20
∴ x = 20

475. Solving equations with variables on both sides...
3x = 2x + 20
Bar Model: Decomposition: Inverse operations:
3x 3x = 2x + 20
2x + 20 x + x + x = x + x + 20
x x x x = 20
x x 20
∴ x = 20

476. Solving equations with variables on both sides...
3x = 2x + 20
Bar Model: Decomposition: Inverse operations:
3x 3x = 2x + 20
2x + 20 x + x + x = x + x + 20
x x x x = 20
x x 20
∴ x = 20

477. Solving equations with variables on both sides...
3x = 2x + 20
Bar Model: Decomposition: Inverse operations:
3x 3x = 2x + 20 3x = 2x + 20
2x + 20 x + x + x = x + x + 20
x x x x = 20
x x 20
∴ x = 20

478. Solving equations with variables on both sides...
3x = 2x + 20
Bar Model: Decomposition: Inverse operations:
3x 3x = 2x + 20 3x = 2x + 20
2x + 20 x + x + x = x + x + 20 3x − 2x = 2x − 2x + 20
x x x x = 20
x x 20
∴ x = 20

479. Solving equations with variables on both sides...
3x = 2x + 20
Bar Model: Decomposition: Inverse operations:
3x 3x = 2x + 20 3x = 2x + 20
2x + 20 x + x + x = x + x + 20 3x − 2x = 2x − 2x + 20
x x x x = 20
x x 20
∴ x = 20

480. Solving equations with variables on both sides...
3x = 2x + 20
Bar Model: Decomposition: Inverse operations:
3x 3x = 2x + 20 3x = 2x + 20
2x + 20 x + x + x = x + x + 20 3x − 2x = 2x − 2x + 20
x x x x = 20
x x 20 x = 20
∴ x = 20

481. Your Turn:
4x + 8 = 5x + 3

482. Your Turn:
4x + 8 = 5x + 3
Bar Model: Decomposition: Inverse operations:

483. Your Turn:
4x + 8 = 5x + 3
Bar Model: Decomposition: Inverse operations:
4x + 8
5x + 3

484. Your Turn:
4x + 8 = 5x + 3
Bar Model: Decomposition: Inverse operations:
4x + 8
5x + 3
4x 8
4x x 3

485. Your Turn:
4x + 8 = 5x + 3
Bar Model: Decomposition: Inverse operations:
4x + 8
5x + 3
4x 8
4x x 3
4x 5 3
4x x 3

486. Your Turn:
4x + 8 = 5x + 3
Bar Model: Decomposition: Inverse operations:
4x + 8
5x + 3
4x 8
4x x 3
4x 5 3
4x x 3
∴ x = 5

487. Your Turn:
4x + 8 = 5x + 3
Bar Model: Decomposition: Inverse operations:
4x + 8
5x + 3
4x 8
4x x 3
4x 5 3
4x x 3
∴ x = 5

488. Your Turn:
4x + 8 = 5x + 3
Bar Model: Decomposition: Inverse operations:
4x + 8 4x + 8 = 5x + 3
5x + 3
4x 8
4x x 3
4x 5 3
4x x 3
∴ x = 5

489. Your Turn:
4x + 8 = 5x + 3
Bar Model: Decomposition: Inverse operations:
4x + 8 4x + 8 = 5x + 3
5x + 3
4x + 8 = 4x + x + 3
4x 8
4x x 3
4x 5 3
4x x 3
∴ x = 5

490. Your Turn:
4x + 8 = 5x + 3
Bar Model: Decomposition: Inverse operations:
4x + 8 4x + 8 = 5x + 3
5x + 3
4x + 8 = 4x + x + 3
4x 8
4x x 3
4x 5 3
4x x 3
∴ x = 5

491. Your Turn:
4x + 8 = 5x + 3
Bar Model: Decomposition: Inverse operations:
4x + 8 4x + 8 = 5x + 3
5x + 3
4x + 8 = 4x + x + 3
4x 8 8 = x + 3
4x x 3
4x 5 3
4x x 3
∴ x = 5

492. Your Turn:
4x + 8 = 5x + 3
Bar Model: Decomposition: Inverse operations:
4x + 8 4x + 8 = 5x + 3
5x + 3
4x + 8 = 4x + x + 3
4x 8 8 = x + 3
4x x 3
5 + 3 = x + 3
4x 5 3
4x x 3
∴ x = 5

493. Your Turn:
4x + 8 = 5x + 3
Bar Model: Decomposition: Inverse operations:
4x + 8 4x + 8 = 5x + 3
5x + 3
4x + 8 = 4x + x + 3
4x 8 8 = x + 3
4x x 3
5 + 3 = x + 3
4x 5 3
4x x 3
∴ x = 5

494. Your Turn:
4x + 8 = 5x + 3
Bar Model: Decomposition: Inverse operations:
4x + 8 4x + 8 = 5x + 3
5x + 3
4x + 8 = 4x + x + 3
4x 8 8 = x + 3
4x x 3
5 + 3 = x + 3
4x 5 3
4x x 3 ∴ 5 = x
∴ x = 5

495. Your Turn:
4x + 8 = 5x + 3
Bar Model: Decomposition: Inverse operations:
4x + 8 4x + 8 = 5x + 3
5x + 3
4x + 8 = 4x + x + 3
4x 8 8 = x + 3
4x x 3
5 + 3 = x + 3
4x 5 3
4x x 3 ∴ 5 = x
∴ x = 5

496. Your Turn:
4x + 8 = 5x + 3
Bar Model: Decomposition: Inverse operations:
4x + 8 4x + 8 = 5x + 3 4x + 8 = 5x + 3
5x + 3
4x + 8 = 4x + x + 3
4x 8 8 = x + 3
4x x 3
5 + 3 = x + 3
4x 5 3
4x x 3 ∴ 5 = x
∴ x = 5

497. Your Turn:
4x + 8 = 5x + 3
Bar Model: Decomposition: Inverse operations:
4x + 8 4x + 8 = 5x + 3 4x + 8 = 5x + 3
5x + 3
4x + 8 = 4x + x + 3 4x − 4x + 8 = 5x − 4x + 3
4x 8 8 = x + 3
4x x 3
5 + 3 = x + 3
4x 5 3
4x x 3 ∴ 5 = x
∴ x = 5

498. Your Turn:
4x + 8 = 5x + 3
Bar Model: Decomposition: Inverse operations:
4x + 8 4x + 8 = 5x + 3 4x + 8 = 5x + 3
5x + 3
4x + 8 = 4x + x + 3 4x − 4x + 8 = 5x − 4x + 3
4x 8 8 = x + 3
4x x 3
5 + 3 = x + 3
4x 5 3
4x x 3 ∴ 5 = x
∴ x = 5

499. Your Turn:
4x + 8 = 5x + 3
Bar Model: Decomposition: Inverse operations:
4x + 8 4x + 8 = 5x + 3 4x + 8 = 5x + 3
5x + 3
4x + 8 = 4x + x + 3 4x − 4x + 8 = 5x − 4x + 3
4x 8 8 = x + 3 8 = x + 3
4x x 3
5 + 3 = x + 3
4x 5 3
4x x 3 ∴ 5 = x
∴ x = 5

500. Your Turn:
4x + 8 = 5x + 3
Bar Model: Decomposition: Inverse operations:
4x + 8 4x + 8 = 5x + 3 4x + 8 = 5x + 3
5x + 3
4x + 8 = 4x + x + 3 4x − 4x + 8 = 5x − 4x + 3
4x 8 8 = x + 3 8 = x + 3
4x x 3
5 + 3 = x + 3 8 − 3 = x + 3 − 3
4x 5 3
4x x 3 ∴ 5 = x
∴ x = 5

501. Your Turn:
4x + 8 = 5x + 3
Bar Model: Decomposition: Inverse operations:
4x + 8 4x + 8 = 5x + 3 4x + 8 = 5x + 3
5x + 3
4x + 8 = 4x + x + 3 4x − 4x + 8 = 5x − 4x + 3
4x 8 8 = x + 3 8 = x + 3
4x x 3
5 + 3 = x + 3 8 − 3 = x + 3 − 3
4x 5 3
4x x 3 ∴ 5 = x
∴ x = 5

502. Your Turn:
4x + 8 = 5x + 3
Bar Model: Decomposition: Inverse operations:
4x + 8 4x + 8 = 5x + 3 4x + 8 = 5x + 3
5x + 3
4x + 8 = 4x + x + 3 4x − 4x + 8 = 5x − 4x + 3
4x 8 8 = x + 3 8 = x + 3
4x x 3
5 + 3 = x + 3 8 − 3 = x + 3 − 3
4x 5 3
4x x 3 ∴ 5 = x 5 = x
∴ x = 5

503. Percent Problems
Mathematics*Center*
West*Contra*Costa**
Unified*School*District*

505. 2) 14 is 2% of what number?

506. 2) 14 is 2% of what number?
is %
=
of 100

507. 2) 14 is 2% of what number?
is %
=
of 100
14 2
=
x 100

508. 2) 14 is 2% of what number?
is %
=
of 100
14 2
=
x 100
2x = 14 • 100

509. 2) 14 is 2% of what number?
is %
=
of 100
14 2
=
x 100
2x = 14 • 100
14 • 100
x=
2

510. 2) 14 is 2% of what number?
is %
=
of 100
14 2
=
x 100
2x = 14 • 100
14 • 100
x=
2
2 • 7 • 100
x=
2

511. 2) 14 is 2% of what number?
is %
=
of 100
14 2
=
x 100
2x = 14 • 100
14 • 100
x=
2
x=
1
2 • 7 • 100
2

512. 2) 14 is 2% of what number?
is %
=
of 100
14 2
=
x 100
2x = 14 • 100
14 • 100
x=
2
x=
1
2 • 7 • 100
2
x = 700

513. 2) 14 is 2% of what number?
is %
=
of 100
14 2
=
x 100
2x = 14 • 100
14 • 100
x=
2
x=
12 • 7 • 100
2
x = 700
14 is 2% of 700.

514. 2) 14 is 2% of what number?
is %
=
of 100 vs
14 2
=
x 100
2x = 14 • 100
14 • 100
x=
2
x=
12 • 7 • 100
2
x = 700
14 is 2% of 700.

515. 2) 14 is 2% of what number?
is % 14 is 2% of what number?
=
of 100 vs
14 2
=
x 100
2x = 14 • 100
14 • 100
x=
2
x=
12 • 7 • 100
2
x = 700
14 is 2% of 700.

516. 2) 14 is 2% of what number?
is % 14 is 2% of what number?
=
of 100 vs
14 2
=
x 100
2x = 14 • 100
14 • 100
x=
2
x=
12 • 7 • 100
2
x = 700
14 is 2% of 700.

517. 2) 14 is 2% of what number?
is % 14 is 2% of what number?
=
of 100 vs
14 2
= 14
x 100
2x = 14 • 100
14 • 100
x=
2
x=
12 • 7 • 100
2
x = 700
14 is 2% of 700.

518. 2) 14 is 2% of what number?
is % 14 is 2% of what number?
=
of 100 vs
14 2
= 14 =
x 100
2x = 14 • 100
14 • 100
x=
2
x=
12 • 7 • 100
2
x = 700
14 is 2% of 700.

519. 2) 14 is 2% of what number?
is % 14 is 2% of what number?
=
of 100 vs
14 2 2
= 14 =
x 100 100
2x = 14 • 100
14 • 100
x=
2
x=
12 • 7 • 100
2
x = 700
14 is 2% of 700.

520. 2) 14 is 2% of what number?
is % 14 is 2% of what number?
=
of 100 vs
14 2 2
= 14 = •
x 100 100
2x = 14 • 100
14 • 100
x=
2
x=
12 • 7 • 100
2
x = 700
14 is 2% of 700.

521. 2) 14 is 2% of what number?
is % 14 is 2% of what number?
=
of 100 vs
14 2 2
= 14 = • x
x 100 100
2x = 14 • 100
14 • 100
x=
2
x=
12 • 7 • 100
2
x = 700
14 is 2% of 700.

522. 2) 14 is 2% of what number?
is % 14 is 2% of what number?
=
of 100 vs
14 2 2
= 14 = • x
x 100 100
2 x
2x = 14 • 100 14 = •
100 1
14 • 100
x=
2
x=
12 • 7 • 100
2
x = 700
14 is 2% of 700.

523. 2) 14 is 2% of what number?
is % 14 is 2% of what number?
=
of 100 vs
14 2 2
= 14 = • x
x 100 100
2 x
2x = 14 • 100 14 = •
100 1
14 • 100 2 • x
x= 14 =
2 2 • 50
x=
12 • 7 • 100
2
x = 700
14 is 2% of 700.

524. 2) 14 is 2% of what number?
is % 14 is 2% of what number?
=
of 100 vs
14 2 2
= 14 = • x
x 100 100
2 x
2x = 14 • 100 14 = •
100 1
x=
14 • 100
2
14 =
12 • x
2 • 50
x=
12 • 7 • 100
2
x = 700
14 is 2% of 700.

525. 2) 14 is 2% of what number?
is % 14 is 2% of what number?
=
of 100 vs
14 2 2
= 14 = • x
x 100 100
2 x
2x = 14 • 100 14 = •
100 1
x=
14 • 100
2
14 =
12 • x
2 • 50
x
x=
12 • 7 • 100
2
x = 700
14 =
50
14 is 2% of 700.

526. 2) 14 is 2% of what number?
is % 14 is 2% of what number?
=
of 100 vs
14 2 2
= 14 = • x
x 100 100
2 x
2x = 14 • 100 14 = •
100 1
x=
14 • 100
2
14 =
1
2 • x
2 • 50
x
x=
12 • 7 • 100
2
x = 700
14 =
50
14 • 50 = x
14 is 2% of 700.

527. 2) 14 is 2% of what number?
is % 14 is 2% of what number?
=
of 100 vs
14 2 2
= 14 = • x
x 100 100
2 x
2x = 14 • 100 14 = •
100 1
x=
14 • 100
2
14 =
1
2 • x
2 • 50
x
x=
12 • 7 • 100
2
x = 700
14 =
50
14 • 50 = x
700 = x
14 is 2% of 700.

528. 2) 14 is 2% of what number?
is % 14 is 2% of what number?
=
of 100 vs
14 2 2
= 14 = • x
x 100 100
2 x
2x = 14 • 100 14 = •
100 1
x=
14 • 100
2
14 =
1
2 • x
2 • 50
x
x=
12 • 7 • 100
2
x = 700
14 =
50
14 • 50 = x
700 = x
14 is 2% of 700. 14 is 2% of 700.

529. 2) 14 is 2% of what number?

530. 2) 14 is 2% of what number?
There are many ways to construct bar models -
many ways to think about the mathematics
or

531. 2) 14 is 2% of what number?
There are many ways to construct bar models -
many ways to think about the mathematics
If 14 is 2%,
or

532. 2) 14 is 2% of what number?
There are many ways to construct bar models -
many ways to think about the mathematics
If 14 is 2%, then 140 is 20%
or

533. 2) 14 is 2% of what number?
There are many ways to construct bar models -
many ways to think about the mathematics
If 14 is 2%, then 140 is 20%
or
20%
140

534. 2) 14 is 2% of what number?
There are many ways to construct bar models -
many ways to think about the mathematics
If 14 is 2%, then 140 is 20%
or
20% 40%
140 140

535. 2) 14 is 2% of what number?
There are many ways to construct bar models -
many ways to think about the mathematics
If 14 is 2%, then 140 is 20%
or
20% 40% 60%
140 140 140

536. 2) 14 is 2% of what number?
There are many ways to construct bar models -
many ways to think about the mathematics
If 14 is 2%, then 140 is 20%
or
20% 40% 60% 80%
140 140 140 140

537. 2) 14 is 2% of what number?
There are many ways to construct bar models -
many ways to think about the mathematics
If 14 is 2%, then 140 is 20%
or
20% 40% 60% 80% 100%
140 140 140 140 140

538. 2) 14 is 2% of what number?
There are many ways to construct bar models -
many ways to think about the mathematics
If 14 is 2%, then 140 is 20%
or
20% 40% 60% 80% 100%
140 140 140 140 140
⎧
⎪
⎨
⎪
⎩
5•140 = 700

539. 2) 14 is 2% of what number?
There are many ways to construct bar models -
many ways to think about the mathematics
If 14 is 2%, then 140 is 20%
or
20% 40% 60% 80% 100%
140 140 140 140 140
⎧
⎪
⎨
⎪
⎩
5•140 = 700
14 is 2% of 700.

540. 2) 14 is 2% of what number?
There are many ways to construct bar models -
many ways to think about the mathematics
If 14 is 2%, then 140 is 20%
14 or
2% 20% 40% 60% 80% 100%
140 140 140 140 140
⎧
⎪
⎨
⎪
⎩
5•140 = 700
14 is 2% of 700.

541. 2) 14 is 2% of what number?
There are many ways to construct bar models -
many ways to think about the mathematics
If 14 is 2%, then 140 is 20%
14 28 or
2% 4% 20% 40% 60% 80% 100%
140 140 140 140 140
⎧
⎪
⎨
⎪
⎩
5•140 = 700
14 is 2% of 700.

542. 2) 14 is 2% of what number?
There are many ways to construct bar models -
many ways to think about the mathematics
If 14 is 2%, then 140 is 20%
14 28 42 or
2% 4% 6% 20% 40% 60% 80% 100%
140 140 140 140 140
⎧
⎪
⎨
⎪
⎩
5•140 = 700
14 is 2% of 700.

543. 2) 14 is 2% of what number?
There are many ways to construct bar models -
many ways to think about the mathematics
If 14 is 2%, then 140 is 20%
14 28 42 56 or
2% 4% 6% 8% 20% 40% 60% 80% 100%
140 140 140 140 140
⎧
⎪
⎨
⎪
⎩
5•140 = 700
14 is 2% of 700.

544. 2) 14 is 2% of what number?
There are many ways to construct bar models -
many ways to think about the mathematics
If 14 is 2%, then 140 is 20%
14 28 42 56 70 or
2% 4% 6% 8% 10% 20% 40% 60% 80% 100%
140 140 140 140 140
⎧
⎪
⎨
⎪
⎩
5•140 = 700
14 is 2% of 700.

545. 2) 14 is 2% of what number?
There are many ways to construct bar models -
many ways to think about the mathematics
If 14 is 2%, then 140 is 20%
14 28 42 56 70 or
2% 4% 6% 8% 10% 20% 40% 60% 80% 100%
140 140 140 140 140
70
⎧
⎪
⎨
⎪
⎩
5•140 = 700
14 is 2% of 700.

546. 2) 14 is 2% of what number?
There are many ways to construct bar models -
many ways to think about the mathematics
If 14 is 2%, then 140 is 20%
14 28 42 56 70 or
2% 4% 6% 8% 10% 20% 40% 60% 80% 100%
140 140 140 140 140
70 is 10%
⎧
⎪
⎨
⎪
⎩
5•140 = 700
14 is 2% of 700.

547. 2) 14 is 2% of what number?
There are many ways to construct bar models -
many ways to think about the mathematics
If 14 is 2%, then 140 is 20%
14 28 42 56 70 or
2% 4% 6% 8% 10% 20% 40% 60% 80% 100%
140 140 140 140 140
70 is 10%
⎧
⎪
⎨
⎪
⎩
700 is 100%
5•140 = 700
14 is 2% of 700.

548. 2) 14 is 2% of what number?
There are many ways to construct bar models -
many ways to think about the mathematics
If 14 is 2%, then 140 is 20%
14 28 42 56 70 or
2% 4% 6% 8% 10% 20% 40% 60% 80% 100%
140 140 140 140 140
70 is 10%
⎧
⎪
⎨
⎪
⎩
700 is 100%
5•140 = 700
14 is 2% of 700. 14 is 2% of 700.

549. 3) 50 is what percent of 200?

550. 3) 50 is what percent of 200?
50 is what percent of 200?

551. 3) 50 is what percent of 200?
50 is what percent of 200?
50

552. 3) 50 is what percent of 200?
50 is what percent of 200?
50 =

553. 3) 50 is what percent of 200?
50 is what percent of 200?
x
50 =
100

554. 3) 50 is what percent of 200?
50 is what percent of 200?
x
50 = •
100

555. 3) 50 is what percent of 200?
50 is what percent of 200?
x
50 = • 200
100

556. 3) 50 is what percent of 200?
50 is what percent of 200?
x
50 = • 200
100
x 200
50 = •
100 1

557. 3) 50 is what percent of 200?
50 is what percent of 200?
x
50 = • 200
100
x 200
50 = •
100 1
x • 2 • 100
50 =
100

558. 3) 50 is what percent of 200?
50 is what percent of 200?
x
50 = • 200
100
x 200
50 = •
100 1
50 =
1
x • 2 • 100
100

559. 3) 50 is what percent of 200?
50 is what percent of 200?
x
50 = • 200
100
x 200
50 = •
100 1
50 =
1
x • 2 • 100
100
50 = 2x

560. 3) 50 is what percent of 200?
50 is what percent of 200?
x
50 = • 200
100
x 200
50 = •
100 1
50 =
1
x • 2 • 100
100
50 = 2x
25 = x

561. 3) 50 is what percent of 200?
50 is what percent of 200?
vs
x
50 = • 200
100
x 200
50 = •
100 1
50 =
1
x • 2 • 100
100
50 = 2x
25 = x 50 is 25% of 200.

562. 3) 50 is what percent of 200?
50 is what percent of 200?
vs
x
50 = • 200
100
x 200
50 = •
100 1
50 =
1
x • 2 • 100
100
50 = 2x
25 = x 50 is 25% of 200.

563. 3) 50 is what percent of 200?
50 is what percent of 200?
vs
50
x
50 = • 200
100
x 200
50 = •
100 1
50 =
1
x • 2 • 100
100
50 = 2x
25 = x 50 is 25% of 200.

564. 3) 50 is what percent of 200?
50 is what percent of 200?
vs
50
x
50 = • 200
100 ? %
x 200
50 = •
100 1
50 =
1
x • 2 • 100
100
50 = 2x
25 = x 50 is 25% of 200.

565. 3) 50 is what percent of 200?
50 is what percent of 200?
vs
50 100
x
50 = • 200
100 ? %
x 200
50 = •
100 1
50 =
1
x • 2 • 100
100
50 = 2x
25 = x 50 is 25% of 200.

566. 3) 50 is what percent of 200?
50 is what percent of 200?
vs
50 100 150
x
50 = • 200
100 ? %
x 200
50 = •
100 1
50 =
1
x • 2 • 100
100
50 = 2x
25 = x 50 is 25% of 200.

567. 3) 50 is what percent of 200?
50 is what percent of 200?
vs
50 100 150 200
x
50 = • 200
100 ? %
x 200
50 = •
100 1
50 =
1
x • 2 • 100
100
50 = 2x
25 = x 50 is 25% of 200.

568. 3) 50 is what percent of 200?
50 is what percent of 200? 25% 50% 75% 100%
vs
50 100 150 200
x
50 = • 200
100 ? %
x 200
50 = •
100 1
50 =
1
x • 2 • 100
100
50 = 2x
25 = x 50 is 25% of 200.

569. 3) 50 is what percent of 200?
50 is what percent of 200? 25% 50% 75% 100%
vs
50 100 150 200
x
50 = • 200
100 ? %
x 200
50 = •
100 1
50 is 25% of 200.
50 =
1
x • 2 • 100
100
50 = 2x
25 = x 50 is 25% of 200.

570. 3) 50 is what percent of 200?

571. 3) 50 is what percent of 200?
The use of bar models help students
develop relational thinking.

572. 3) 50 is what percent of 200?
The use of bar models help students
develop relational thinking.
or
25% 50% 75% 100%
50 100 150 200
? %
50 is 25% of 200.

573. 3) 50 is what percent of 200?
The use of bar models help students
develop relational thinking.
or
25% 50% 75% 100%
50 100 150 200
? %
50 is 25% of 200.

574. 3) 50 is what percent of 200?
The use of bar models help students
develop relational thinking.
200 is 100%
or
⎩
⎪
⎨
⎪
⎧
25% 50% 75% 100%
50 100 150 200
? %
50 is 25% of 200.

575. 3) 50 is what percent of 200?
The use of bar models help students
develop relational thinking.
200 is 100%
or
⎩
⎪
⎨
⎪
⎧
25% 50% 75% 100%
50 100 150 200
? %
⎧
⎪
⎨
⎪
⎩
⎧
⎪
⎨
⎪
⎩
100 100
50 is 25% of 200.

576. 3) 50 is what percent of 200?
The use of bar models help students
develop relational thinking.
200 is 100%
or
⎩
⎪
⎨
⎪
⎧
25% 50% 75% 100%
50 100 150 200
50 50 50 50
? %
⎧
⎪
⎨
⎪
⎩
⎧
⎪
⎨
⎪
⎩
100 100
50 is 25% of 200.

577. 3) 50 is what percent of 200?
The use of bar models help students
develop relational thinking.
200 is 100%
or
⎩
⎪
⎨
⎪
⎧
25% 50% 75% 100% 25% 50% 75% 100%
50 100 150 200
50 50 50 50
? %
⎧
⎪
⎨
⎪
⎩
⎧
⎪
⎨
⎪
⎩
100 100
50 is 25% of 200.

578. 3) 50 is what percent of 200?
The use of bar models help students
develop relational thinking.
200 is 100%
or
⎩
⎪
⎨
⎪
⎧
25% 50% 75% 100% 25% 50% 75% 100%
50 100 150 200
50 50 50 50
? %
⎧
⎪
⎨
⎪
⎩
⎧
⎪
⎨
⎪
⎩
100 100
50 is 25% of 200. 50 is 25% of 200.

579. 150% of what number is 12?

580. 150% of what number is 12?

581. 150% of what number is 12?
150% = 12
⎩
⎪
⎨
⎪
⎧

582. 150% of what number is 12?
150% = 12
⎩
⎪
⎨
⎪
⎧
50% 100% 150%

583. 150% of what number is 12?
150% = 12
⎩
⎪
⎨
⎪
⎧
4 4 4
50% 100% 150%

584. 150% of what number is 12?
150% = 12
⎩
⎪
⎨
⎪
⎧
4 4 4
50% 100% 150%

585. 150% of what number is 12?
150% = 12
⎩
⎪
⎨
⎪
⎧
4 4 4
50%
⎧ 100% 150%
⎪
⎨
⎪
⎩
8

586. 150% of what number is 12?
150% = 12
⎩
⎪
⎨
⎪
⎧
4 4 4
50%
⎧ 100% 150%
⎪
⎨
⎪
⎩
8
150% of 8 is 12.

587. 150% of what number is 12?

588. 150% of what number is 12?

589. 150% of what number is 12?

590. 150% of what number is 12?

591. 150% of what number is 12?

592. 150% of what number is 12?

593. 150% of what number is 12?
Notice – 200% of 8 is 16?