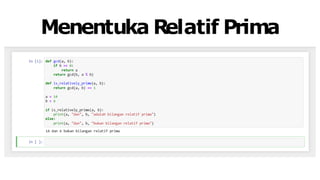
Teori bilangan adalah bidang dasar dalam memahami algoritma kriptografi yang membahas tentang bilangan bulat. Dalam teori ini, konsep seperti pembagian, pembagi bersama terbesar (pbb), bilangan prima, serta berbagai sistem bilangan (desimal, biner, oktal, heksadesimal) diperkenalkan. Proses konversi antara sistem bilangan dan beberapa teorema seperti teorema Euclidean juga dijelaskan.