Downloaded 10 times
TeamLabLT20120630
- 1.
- 2. 自己紹介 @tayama0324 (Takashi Tayama) 会津大 -> 会津大院 -> 会社員 ICPC2006-2010 Contestant OB/OG会メンバー 元AOJ管理人お手伝い
- 3.
- 4. 幾何問題の95%は 1. 最終防衛問題 -> 2. ライブラリをコピペするだけ ->
- 5. 幾何問題の95%は 1. 最終防衛問題 -> あきらめる 2. ライブラリをコピペするだけ -> 絶対に解く！！！
- 6. 手を出してはいけない幾何の例 2007 Domestic: くるくる AOJ1151 回すだけ
- 7. 解くべき幾何の例 2009 Regional (Tokyo): Separate Points AOJ1298 凸包 + 交差判定 するだけ
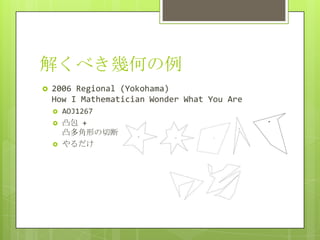
- 8. 解くべき幾何の例 2006 Regional (Yokohama) How I Mathematician Wonder What You Are AOJ1267 凸包 + 凸多角形の切断 やるだけ
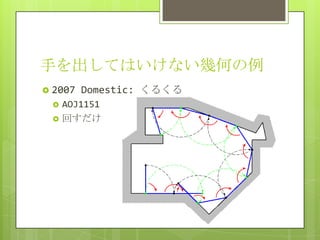
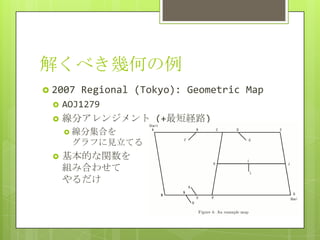
- 9. 解くべき幾何の例 2007 Regional (Tokyo): Geometric Map AOJ1279 線分アレンジメント (+最短経路) 線分集合を グラフに見立てる 基本的な関数を 組み合わせて やるだけ
- 10. 日本ICPCの幾何の傾向 国内予選 最終防衛幾何は毎年出題されている 解ける幾何はあまり出題されない 2008: 大玉転がし (AOJ1157) ぐらい アジア地区予選 解ける幾何・最終防衛幾何 1 問ずつ程度 ここ2年は減少傾向？ 世界的に見ても日本の幾何は多く難しい OB会の練習会では頻出
- 11. 日本ICPCの幾何の傾向 最近は減少傾向にあるものの、 ライブラリさえあれば 短時間で簡単に解ける問題が頻出 模擬予選やその他のコンテストでも 幾何ライブラリを作りましょう！ ライブラリを作る時間は無制限 オンラインジャッジを埋めるのにも便利 最終防衛に挑むのにもやっぱりライブラリは必要 これはもう作るしか！
- 12. ライブラリの作り方 1. どんな関数を作る？ 2. どうやって実装する？ 3. どうやってテストする？
- 13. どんな関数を作る？ 例: 私のライブラリ 内積・外積 多角形と点の包含判定 ccw {直線,線分}と線分の交差判定 3点のなす角度 線分と{線分,点}の距離 線分の交点 2円の共通{内接線,外接線} 多角形の面積 凸多角形の切断 凸包
- 14. どうやって作る？ 偉い人のコードを丸写し！ やめましょう 十分テストしたはずのライブラリが コンテスト本番になってバグることも 自分が使うライブラリがどう動いてるのか 理解しておきましょう でないとデバッグできない
- 15. どうやって作る？ ぼくのかんがえたさいきょうのライブラリを つくろう！ 勉強になるのでとても良いです 一方、下手に作ると 関数どうしの依存関係が複雑になったり 誤差に弱かったり 偉い人のライブラリはよくできている 敬意を払って参考にしつつ、自分好みに改造す るのも良い
- 16. 偉い人 Spaghetti Source (前原さん) http://www.prefield.com/algorithm/inde x.html kkntkr / Unknown wiki (にゃあさん) http://nya3.jp/libicpc/ おまけ: 私のライブラリ https://www.dropbox.com/sh/yw0hqjrln2b fv55/BxqvPOwQoJ/geometry.cpp
- 17. おまけ: 複素平面 2次元幾何は複素数を使って実装されること が多い (C++) typedef std::complex<double> Point; メリット 四則演算子がオーバーロードされている 加減算はベクトルの足し引きなどに 乗除算は点の回転になどに便利 CやJavaでは自前で実装することが多い
- 18. どうやってテストする？ 作ったライブラリが正しく動くことを確信す るために、入念なテストは必須 偉い人は検証に使ったオンラインジャッジの 問題番号をメモしてくれている ランダム入力を大量に作るのもよい どんなに入念にテストしても、本番では1%ぐ らいライブラリを疑っておきましょう
- 19. まとめ ライブラリの力で本番での労力をぐっと減ら せるのが幾何の醍醐味 ライブラリは気合と根性と時間があれば誰に でも作れます レッツ幾何！