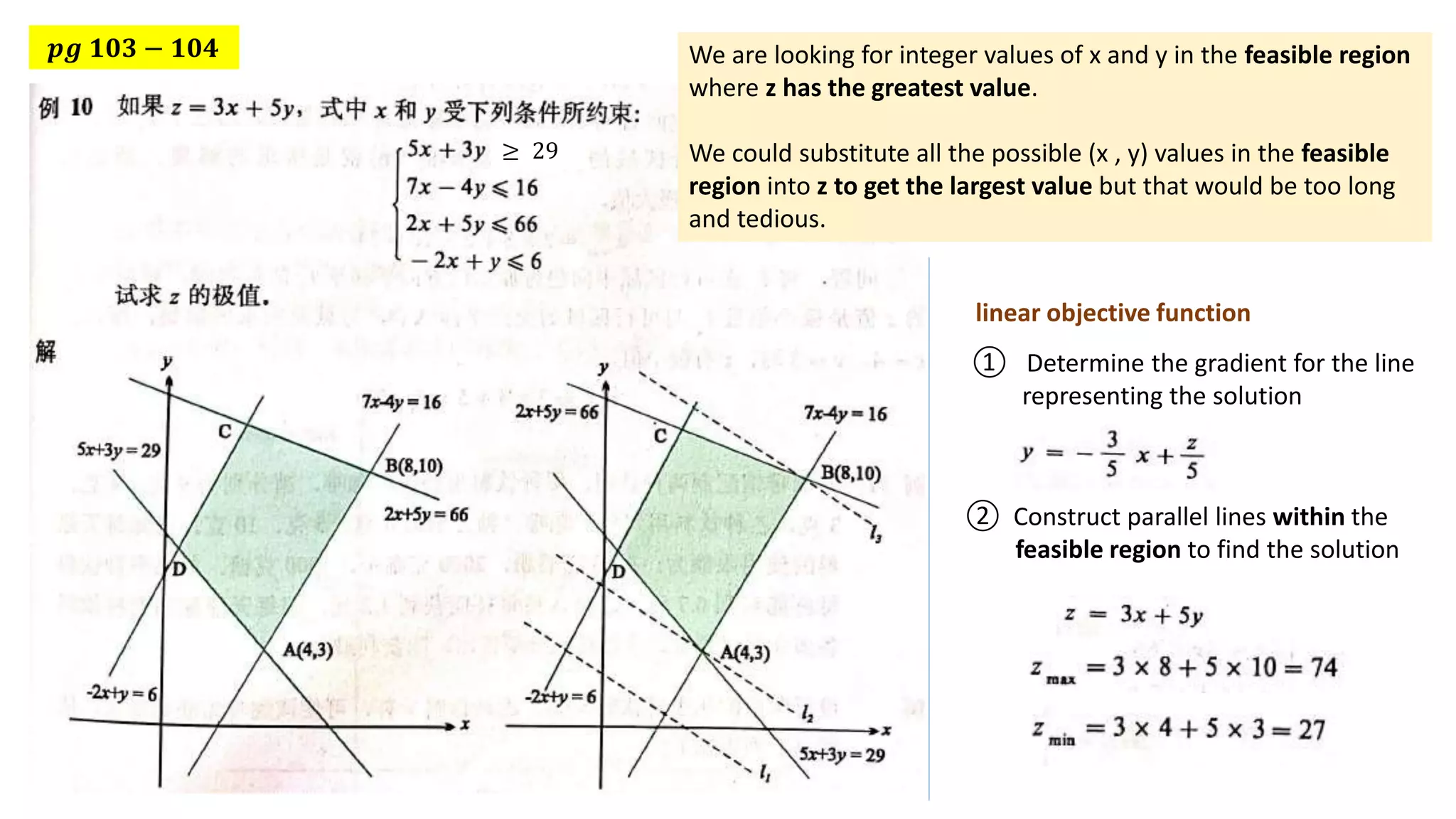
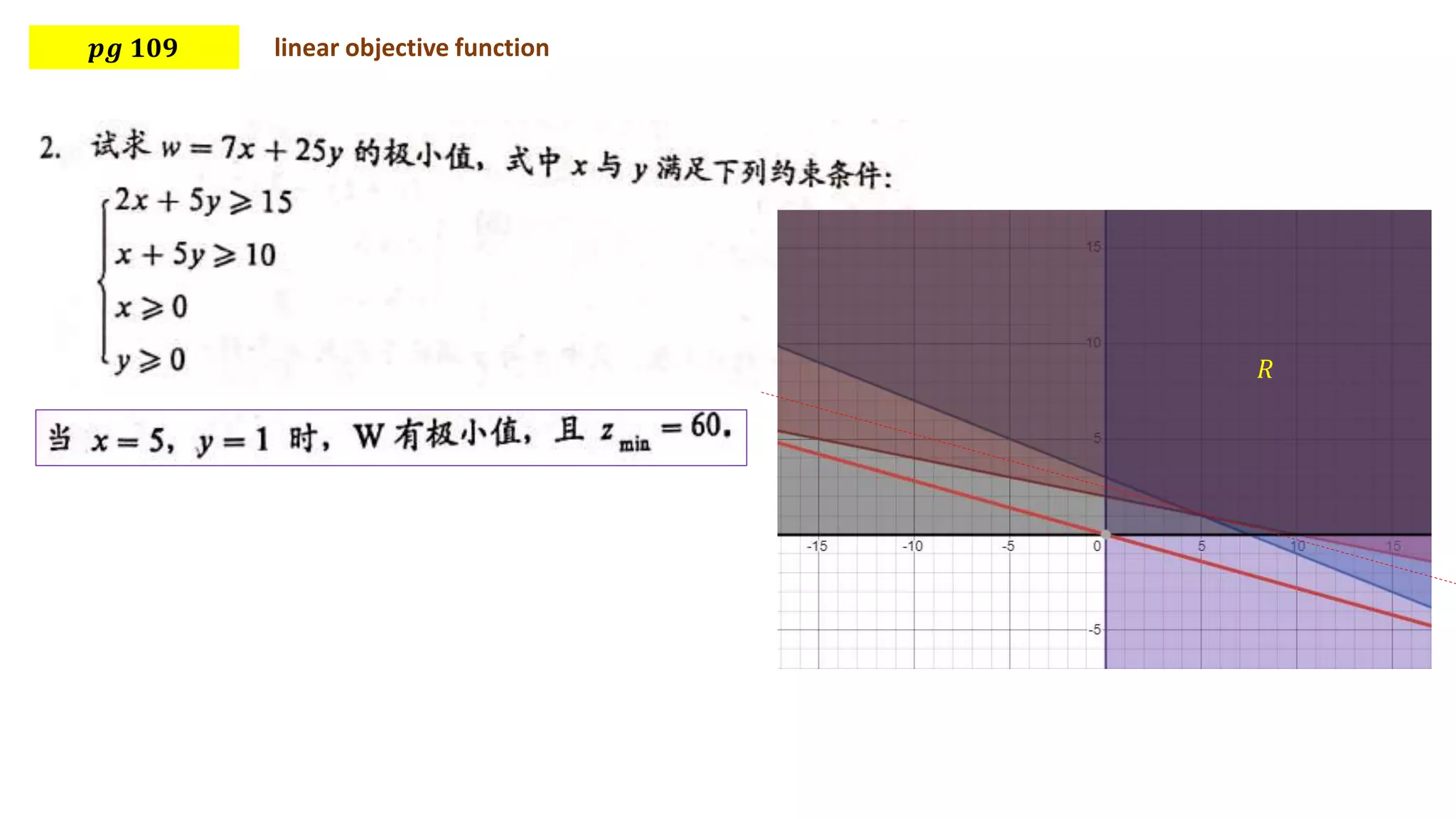
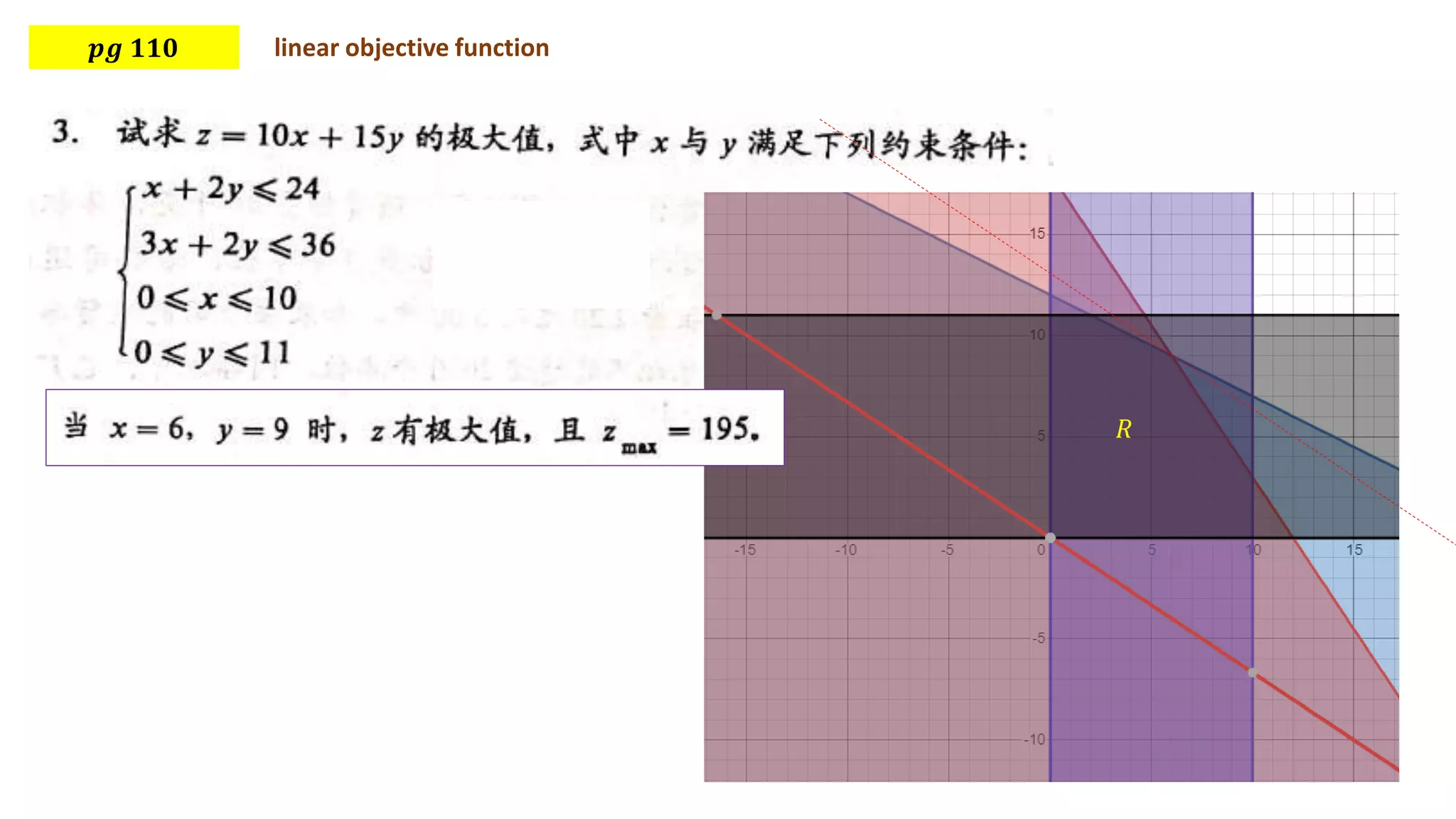
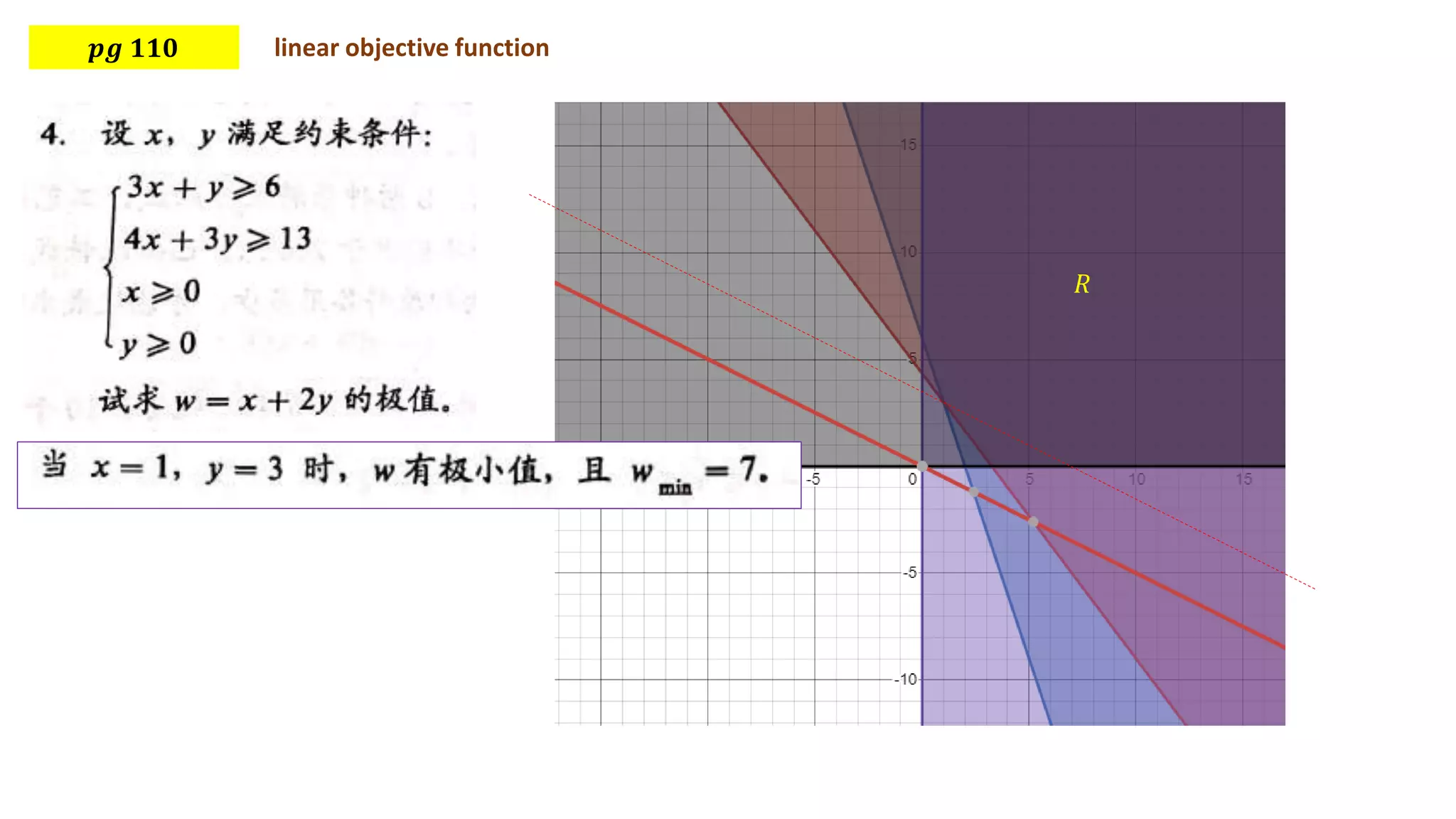
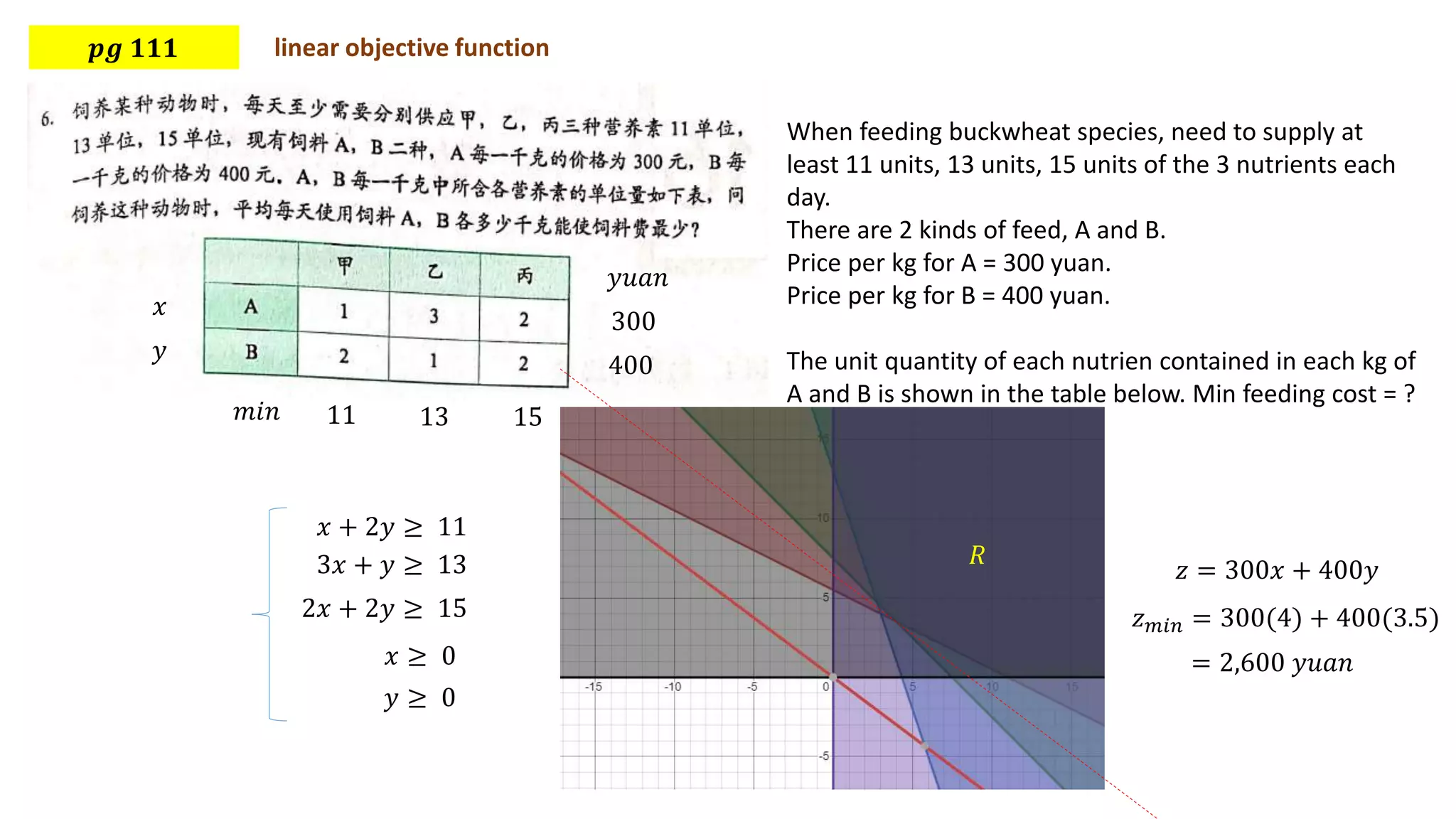
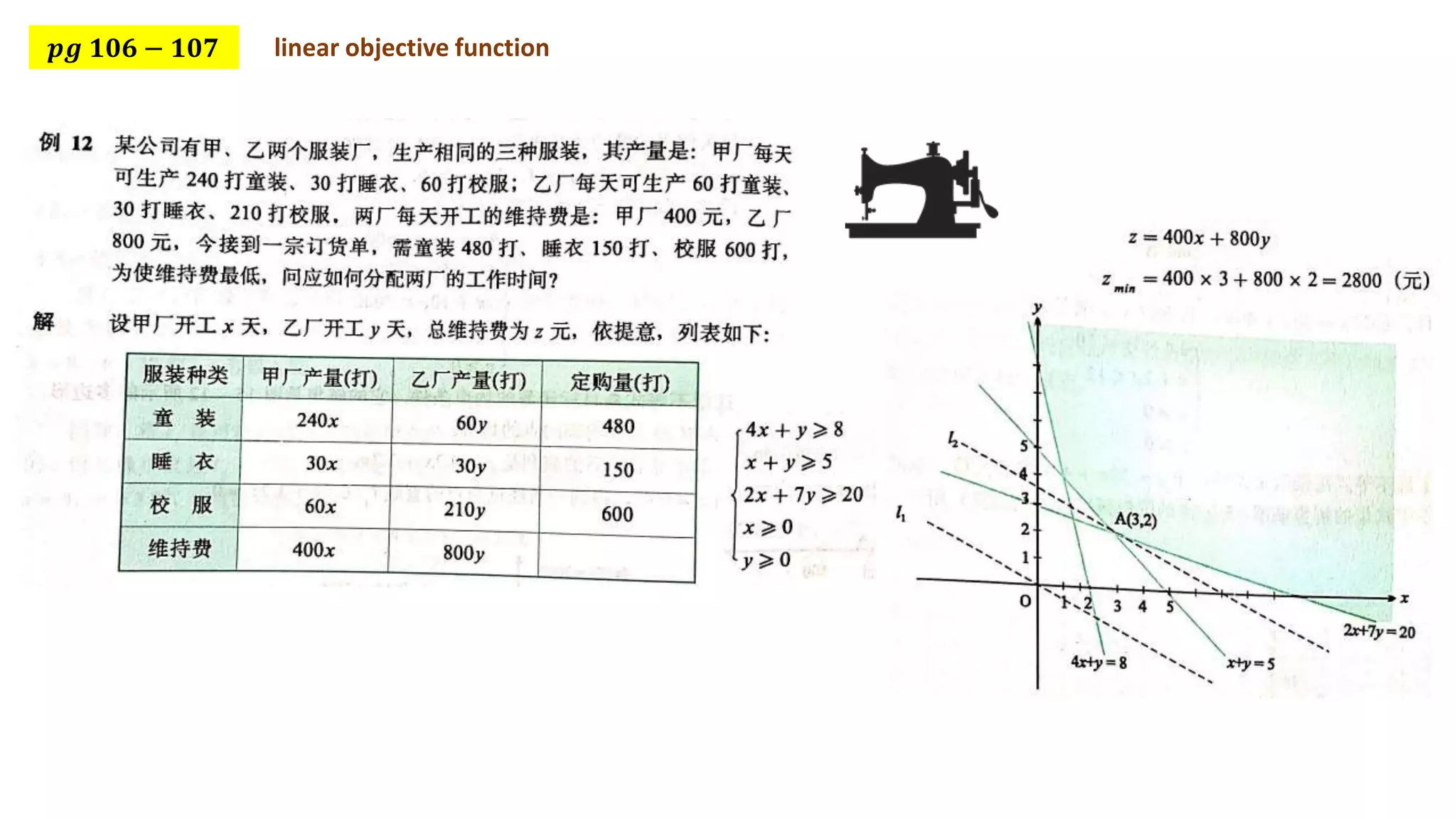
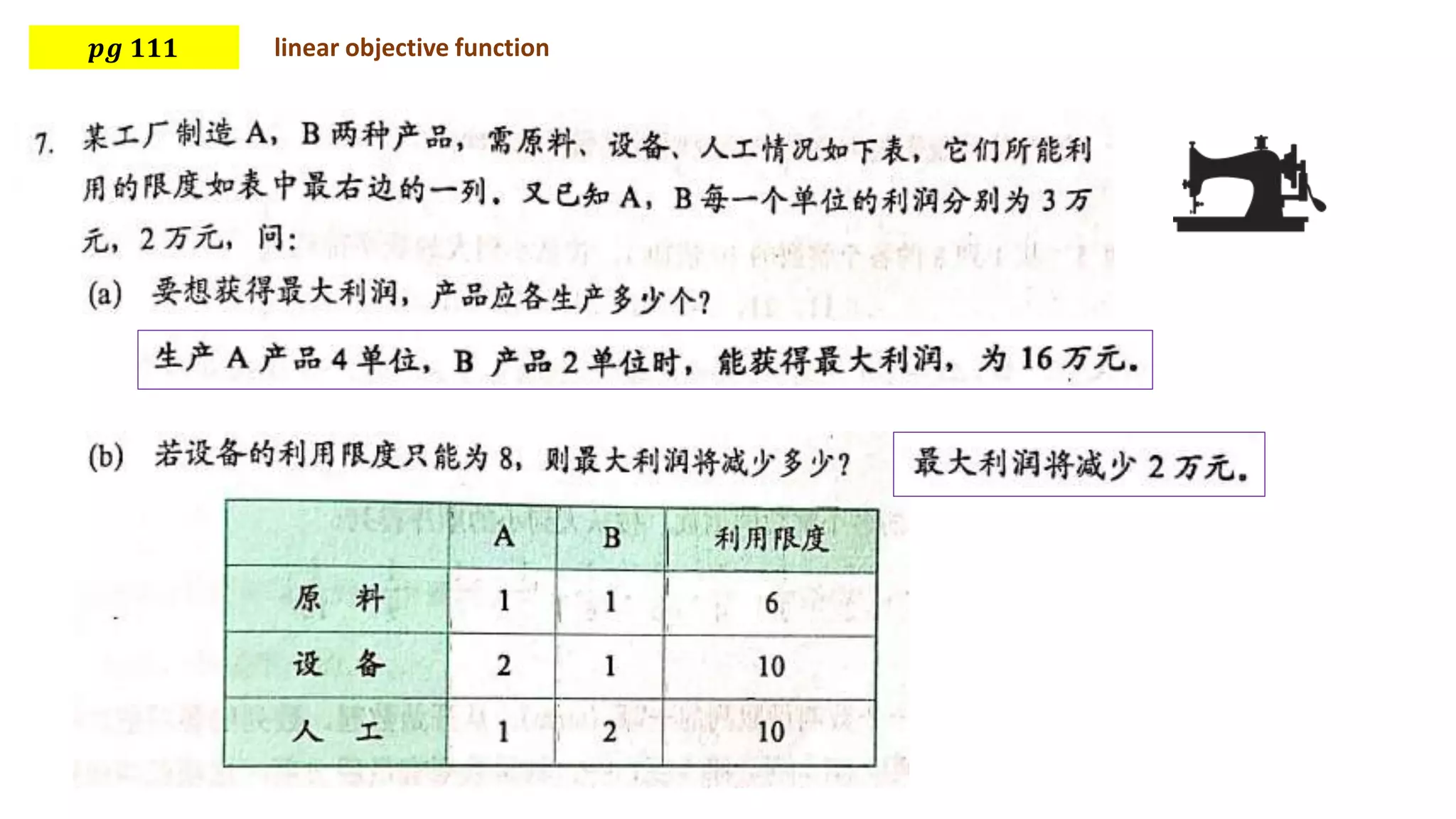
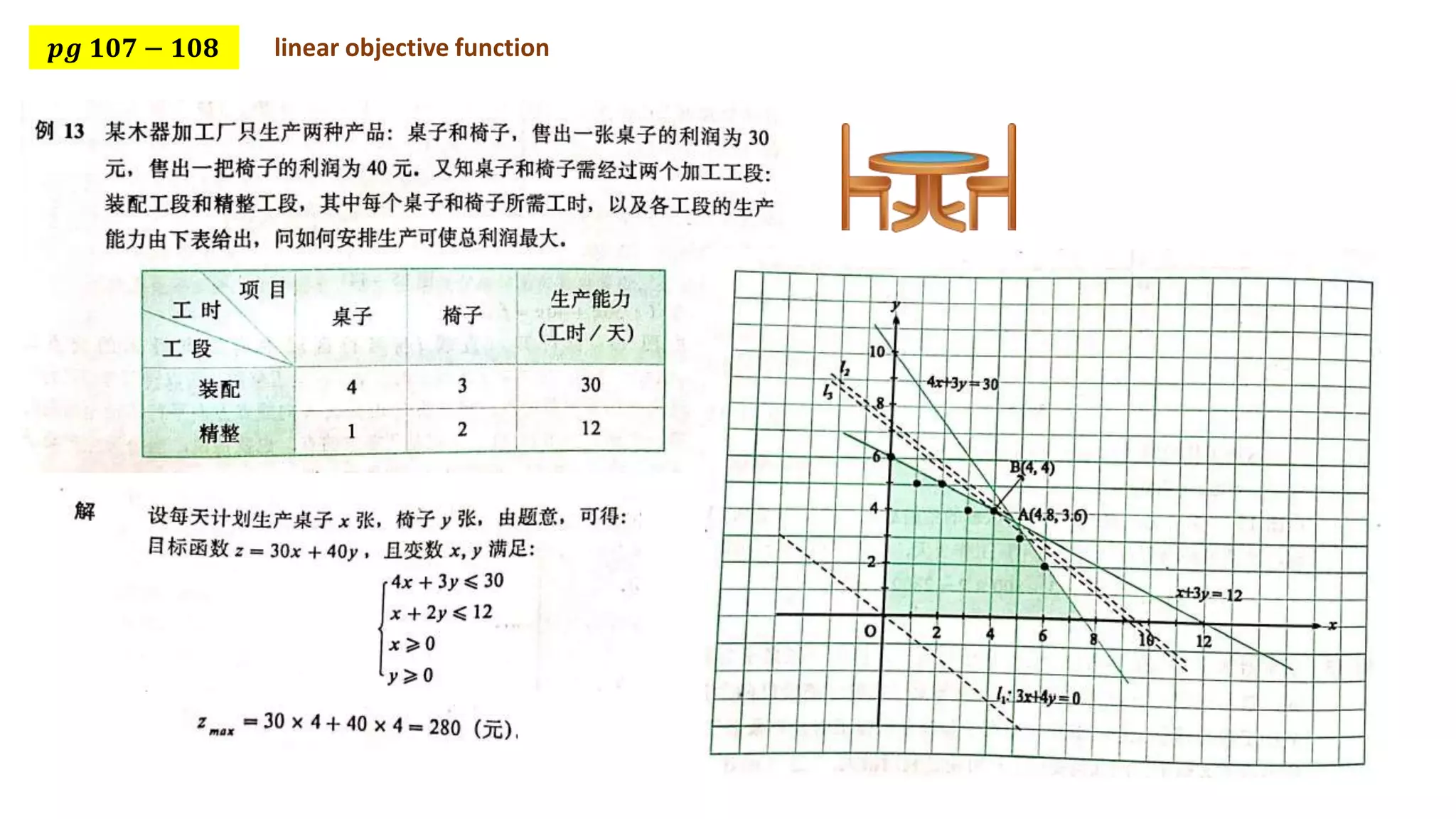
This document discusses using linear programming to solve optimization problems by finding the maximum or minimum value of an objective function subject to certain constraints. It provides two examples: 1) minimizing the cost of feeding buckwheat with two types of feed and nutrient constraints, and 2) maximizing the revenue from transporting goods with two factories subject to weight and volume constraints. Both examples set up the objective function and constraints, then solve to find the optimal value.

1. 𝒑𝒈 𝟏𝟎𝟑 − 𝟏𝟎𝟒
≥ 29
We are looking for integer values of x and y in the feasible region
where z has the greatest value.
We could substitute all the possible (x , y) values in the feasible
region into z to get the largest value but that would be too long
and tedious.
linear objective function
① Determine the gradient for the line
representing the solution
② Construct parallel lines within the
feasible region to find the solution

2. 𝒑𝒈 𝟏𝟎𝟗 linear objective function
𝑅

3. 𝒑𝒈 𝟏𝟎𝟗 linear objective function
𝑅

4. 𝒑𝒈 𝟏𝟏𝟎 linear objective function
𝑅

5. 𝒑𝒈 𝟏𝟏𝟎 linear objective function
𝑅

6. 𝒑𝒈 𝟏𝟎𝟒 − 𝟏𝟎𝟔 linear objective function

7. 𝒑𝒈 𝟏𝟏𝟏 linear objective function

8. When feeding buckwheat species, need to supply at
least 11 units, 13 units, 15 units of the 3 nutrients each
day.
There are 2 kinds of feed, A and B.
Price per kg for A = 300 yuan.
Price per kg for B = 400 yuan.
The unit quantity of each nutrien contained in each kg of
A and B is shown in the table below. Min feeding cost = ?
𝒑𝒈 𝟏𝟏𝟏 linear objective function
300
400
𝑦𝑢𝑎𝑛
11 13 15
𝑚𝑖𝑛
𝑥
𝑦
𝑥 + 2𝑦 ≥ 11
3𝑥 + 𝑦 ≥ 13
2𝑥 + 2𝑦 ≥ 15
𝑥 ≥ 0
𝑦 ≥ 0
𝑅
𝑧 = 300𝑥 + 400𝑦
𝑧𝑚𝑖𝑛 = 300(4) + 400(3.5)
= 2,600 𝑦𝑢𝑎𝑛

9. 𝒑𝒈 𝟏𝟎𝟔 − 𝟏𝟎𝟕 linear objective function

10. 𝒑𝒈 𝟏𝟏𝟏 linear objective function

11. 𝒑𝒈 𝟏𝟎𝟕 − 𝟏𝟎𝟖 linear objective function

12. 𝒑𝒈 𝟏𝟎𝟗 linear objective function

13. 𝒑𝒈 𝟏𝟎𝟗 linear objective function
A transportation company can load good for 2 factories,
A and B.
Factory A box = 2 * 40 kg charge per box = 2.20 yuan
Factory B box = 3 * 50 kg charge per box = 3.00 yuan
Truck max weight = 37,000 kg
Truck max volume = 2,000 boxes
Max charge = ?
A B max
Weight 40 50 37,000
Volume (box) 2 3 2,000
Charge per box
(yuan)
2.20 3.00 ?
4𝑥 + 5𝑦 ≤ 3,700
2𝑥 + 3𝑦 ≤ 2,000
𝑥 ≥ 0
𝑦 ≥ 0
𝑅
𝑧 = 2.20𝑥 + 3𝑦
𝑧𝑚𝑎𝑥 = 2.20(550) + 3(300)
= 2,110 𝑦𝑢𝑎𝑛
𝑠𝑖𝑚𝑝𝑙𝑖𝑓𝑦 𝑡ℎ𝑒 𝑒𝑞𝑢𝑎𝑡𝑖𝑜𝑛

14. 𝒑𝒈 𝟏𝟎𝟗 − 𝟏𝟏𝟏 linear objective function

15. 𝒑𝒈 𝟏𝟎𝟗 − 𝟏𝟏𝟏 linear objective function