Download to read offline
Uploaded bykadek supadma
Stream cipher 1488292373
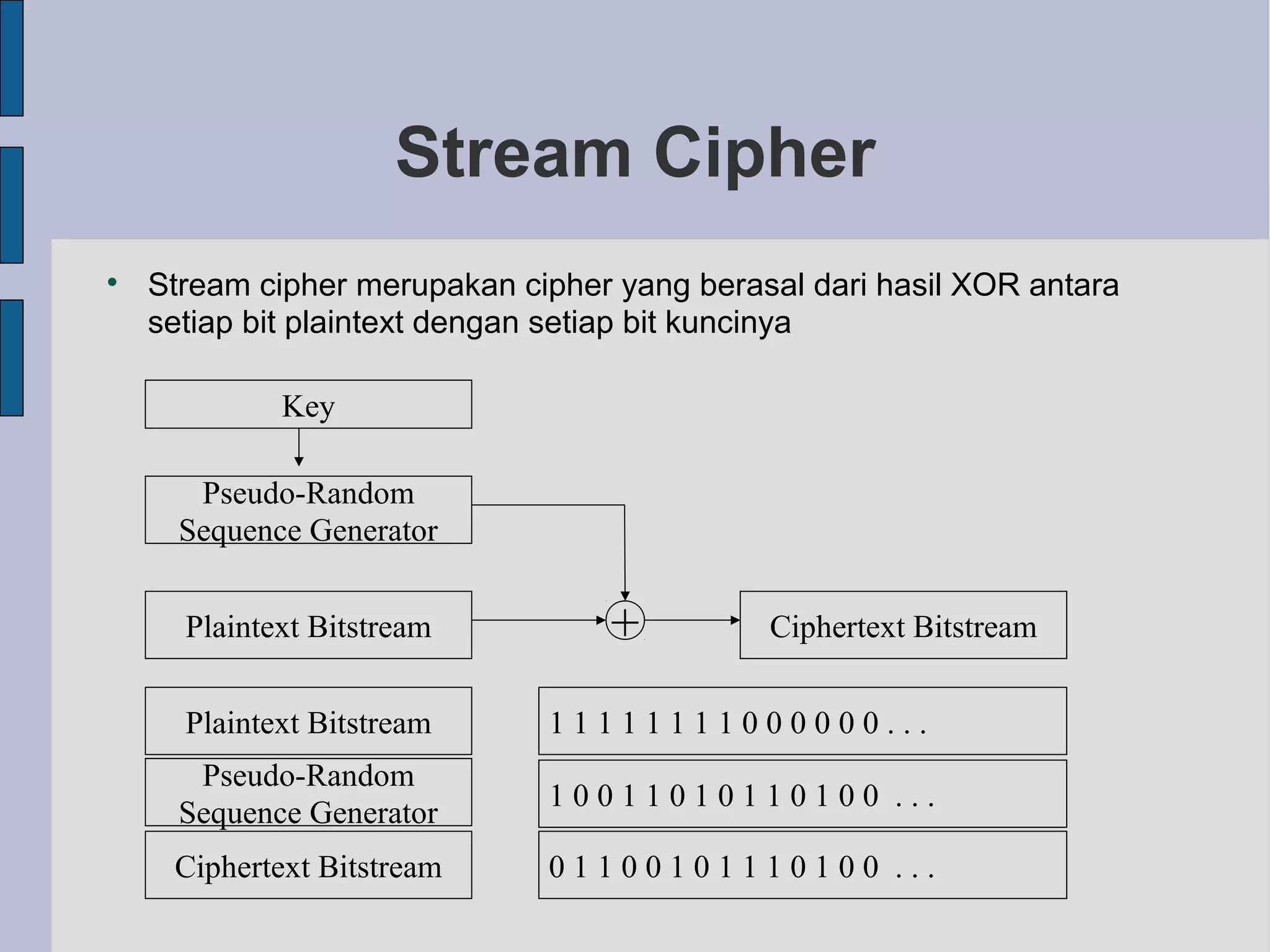
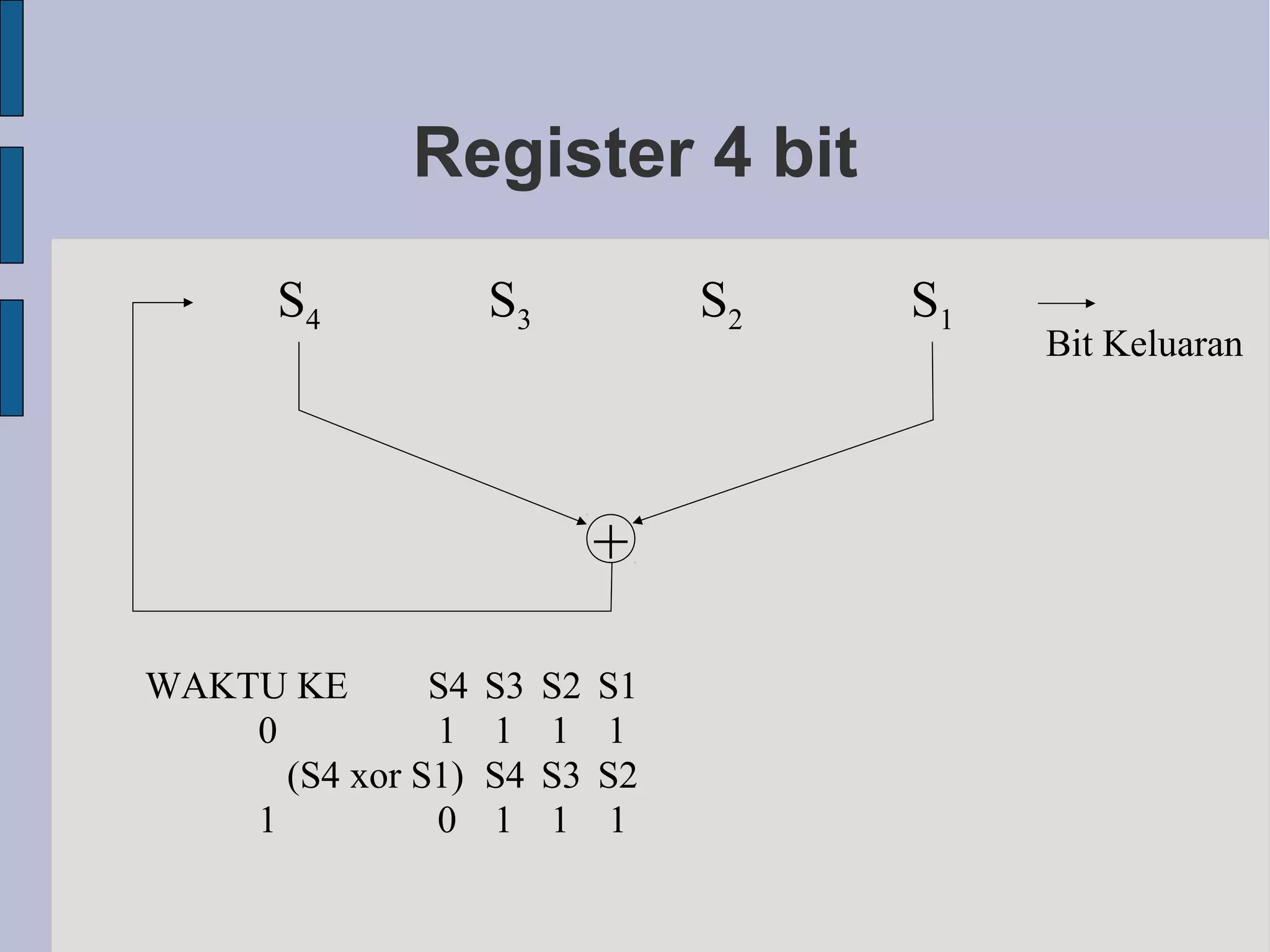
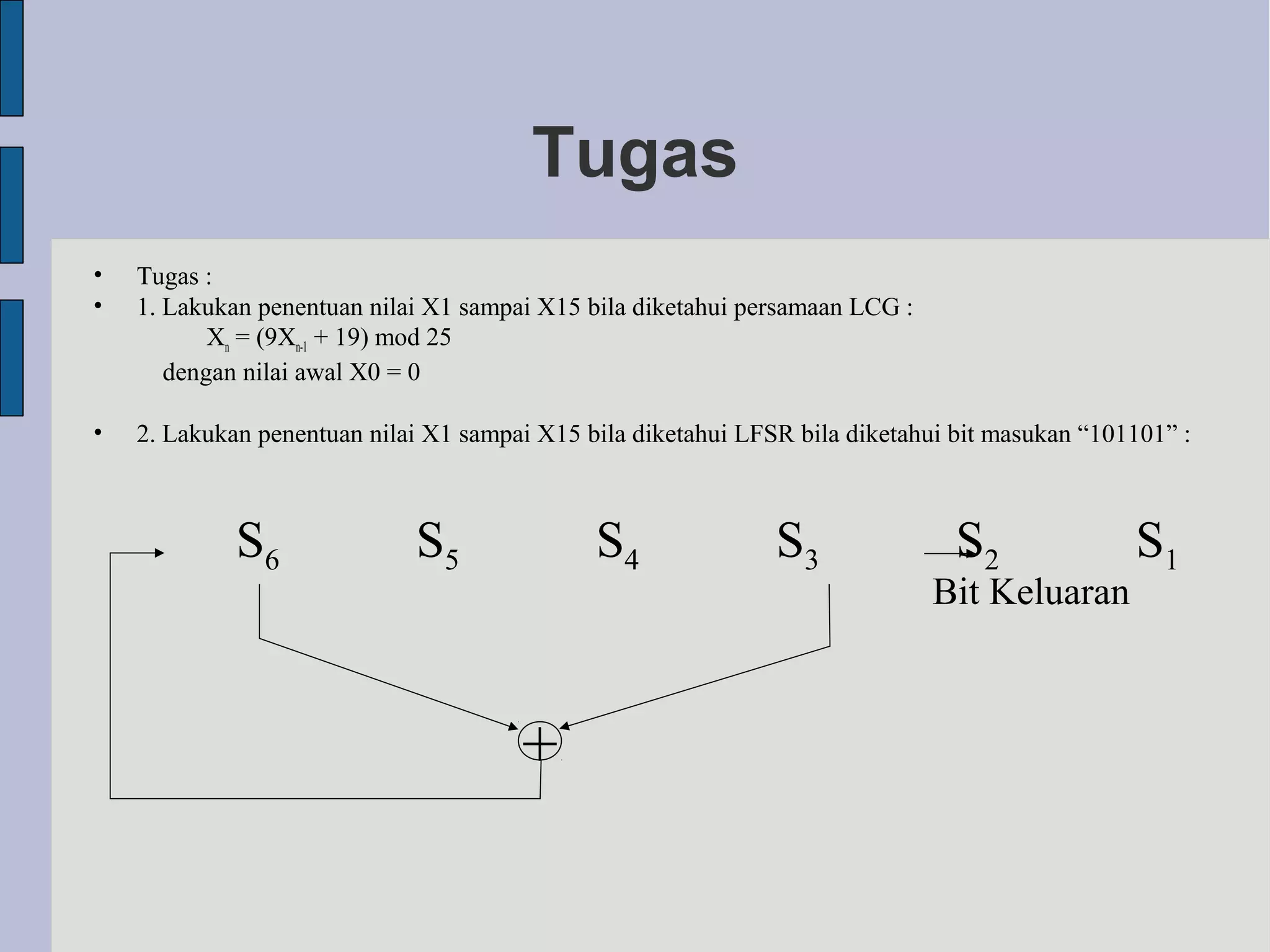
Stream cipher melakukan enkripsi dengan melakukan operasi XOR antara plaintext dan kunci pseudo-random. One-time pad (OTP) merupakan stream cipher teraman karena setiap kunci hanya digunakan sekali, namun kuncinya harus sepanjang plaintext. Pembangkit bilangan acak seperti LCG dan LFSR sering digunakan untuk menghasilkan kunci pseudo-random pada stream cipher.
Stream cipher 1488292373
- 1. Stream Cipher Stream ciphermerupakan cipher yang berasal dari hasil XOR antara setiap bit plaintext dengan setiap bit kuncinya Key Pseudo-Random Sequence Generator Plaintext Bitstream + Ciphertext Bitstream Plaintext Bitstream Pseudo-Random Sequence Generator Ciphertext Bitstream 1 1 1 1 1 1 1 1 0 0 0 0 0 0 . . . 1 0 0 1 1 0 1 0 1 1 0 1 0 0 . . . 0 1 1 0 0 1 0 1 1 1 0 1 0 0 . . .
- 2. Kelemahan Stream Cipher Streamcipher rawan terhadap attack pembalikan bit. Contoh : Misalkan terdapat transfer antar rekening di sebuah bank sejumlah 10 USD untuk sebuah transaksi. Plaintext : QT= TRANSFER USD $000010,00 FRM ACCNT 12345-67 TO Ciphertext : aMz0rapLtxMfpUn7UxOrtIm42ZuweeMDqzPtI7wEptAnxfL 00101101 Flip low bit 00101100 Ciphertext : aMz0rapLtxMfpUn7TxOrtIm42ZuweeMDqzPtI7wEptAnxfL Plaintext : QT= TRANSFER USD $100010,00 FRM ACCNT 12345-67 TO
- 3. One Time Pad OTPtermasuk stream cipher yang ditemukan oleh Mayor J Maugborne dan G. Vernam (1917) Setiap kunci digunakan hanya digunakan untuk sekali pesan Contoh : Acuan : “ A B C D … Z “ “ 1 2 3 4 26 “ Pesan : “KRIPTO” = “11 18 … “ Kuncinya : “TIMBWD” = “20 9 … “ Ciphernya : “EAVRQS” = “ 5 … “ Karena K + T mod 26 = E(11+20 – 26 = 5 = E)
- 4. OTP bilangan biner Rumusenkripsinya : Plaintext XOR kunci = cipher Plaintext A (65) = 0100 0001 Kunci K1= 1101 0100 Ciphertext C = A xor K1 = 1001 0101 Rumus dekripsinya : Ciphertext xor kunci = plaintext Ciphertext C (67) = 1001 0101 Kunci K1= 1101 0100 Plaintext A = C xor K1 = 0100 0001
- 5. Kesempurnaan OTP Contoh : PlaintextB = 0100 0010 Plaintext D = 0100 0100 Kunci K2 = 1101 0111 Kunci K3 = 1101 0001 Ciphertext C = 1001 0101 Ciphertext C = 1001 0101 Analisa : bila kita tidak tahu kuncinya maka dengan hanya diketahui ciphertextnya saja maka belum tentu diketahui plaintextnya. Namun bila K yang sama digunakan untuk beberapa kali enkripsi dengan pesan yang berbeda, maka keamanan akan hilang. Contoh : Plaintext B = 0100 0010 Plaintext D = 0100 0100 Kunci K2 = 1101 0111 Kunci K2 = 1101 0111 Ciphertext C1 = 1001 0101 Ciphertext C2 = 1001 0011 Ini menimbulkan bahwa B xor D = C1 xor C2
- 6. Pembangkit Deret BilanganAcak Semu • Deret bilangan acak yang dibangkitkan dari rumus matematika dianggap sebagai deret acak semu • Pembangkit bilangan acak yang sering digunakan adalah LCG (Linier Congruential Generators) Xn = (aXn-1 + b) mod m misalkan : Xn = (7Xn-1 + 11) mod 17 untuk n=1 nilai X0= 0 X1 = (7X0 + 11) mod 17 X1 = 11
- 7. Hasil komputasi lengkapuntuk sejumlah nilai n adalah : n Xn n Xn n Xn n Xn 1 11 7 6 13 12 19 15 2 3 8 2 14 10 20 14 3 15 9 8 15 13 21 7 4 14 10 16 16 0 22 9 5 7 11 4 17 11 23 6 6 9 12 5 18 3 24 2
- 8. Linear Feedback ShiftRegister (LFSR) LFSR (Register Geser dengan Umpan Balik Linear) Digunakan baik pada kriftografi maupun teori pengkodean Sering digunakan oleh militer sejak permulaan penggunaan peralatan elektronik. Keunggulannya mudah diimplementasikan pada perangkat keras
- 9. Register 4 bit S4S3 S2 S1 + Bit Keluaran WAKTU KE S4 S3 S2 S1 0 1 1 1 1 (S4 xor S1) S4 S3 S2 1 0 1 1 1
- 10. Hasil LFSR Waktu keS4 S3 S2 S1 Waktu ke S4 S3 S2 S1 0 1 1 1 1 11 0 0 0 1 1 0 1 1 1 12 1 0 0 0 2 1 0 1 1 13 1 1 0 0 3 0 1 0 1 14 1 1 1 0 4 1 0 1 0 15 1 1 1 1 5 1 1 0 1 16 0 1 1 1 6 0 1 1 0 17 1 0 1 1 7 0 0 1 1 18 0 1 0 1 8 1 0 0 1 19 1 0 1 0 9 0 1 0 0 20 1 1 0 1 10 0 0 1 0 21 0 1 1 0
- 11. Tugas • Tugas : •1. Lakukan penentuan nilai X1 sampai X15 bila diketahui persamaan LCG : Xn = (9Xn-1 + 19) mod 25 dengan nilai awal X0 = 0 • 2. Lakukan penentuan nilai X1 sampai X15 bila diketahui LFSR bila diketahui bit masukan “101101” : + Bit Keluaran S6 S5 S4 S3 S2 S1