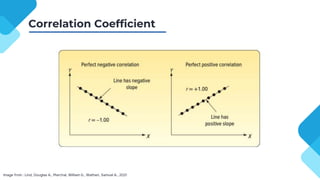
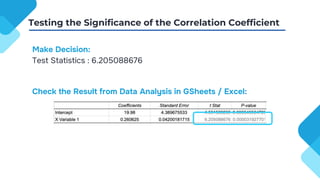
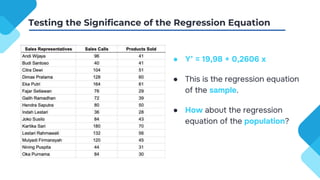
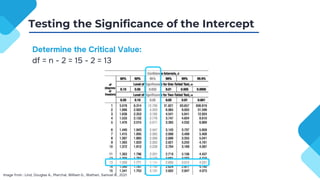
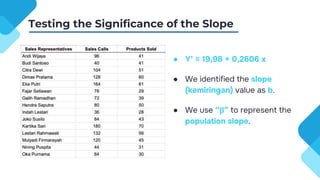
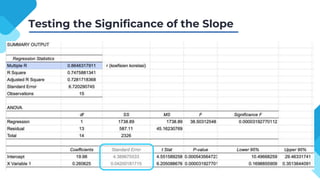
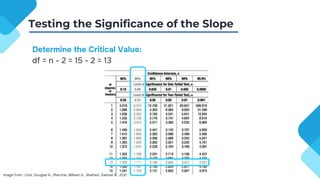
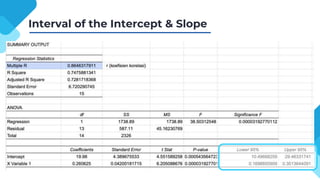
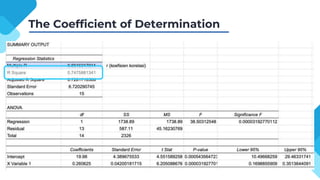
The document discusses correlation and regression analysis, detailing techniques to measure relationships between variables and develop predictive equations. It explains the significance of correlation coefficients and regression equations, including testing hypotheses about the population using inferential statistics. Additionally, it highlights the proportion of variance explained by independent variables, with an example showing a specific regression equation and its interpretations.

1. Statistics 1
13
Correlation & Linear
Regression 2
Muhammad Rifqi Arviansyah

2. https://linktr.ee/bisdi_
aping

3. Present Form - System
Pada bagian komentar silahkan
isi:
1. Hal yang saya pelajari hari ini.
2.Hal menarik dari perkuliahan
hari ini.
3.Hal yang masih ingin saya cari
tahu setelah perkuliahan ini.
4.Saran.

4. Previously on Stat 1….

5. ● Correlation Analysis
Group of techniques to measure the relationship between
two variables.
● Regression Analysis
Develop an equation that will allow us to estimate the
value of one variable based on the value of another.
Correlation Analysis & Regression Analysis

6. Correlation Coefficient
Image from : Lind, Douglas A., Marchal, William G., Wathen, Samuel A., 2021

7. Correlation Coefficient Category
Image from : Lind, Douglas A., Marchal, William G., Wathen, Samuel A., 2021
From Cohen 1988:
1. Weak : 0.10 - 0.29
2. Medium : 0.30 - 0.49
3. Large : 0.50 - 1.00
From Evans 1996:
1. Very weak : 0.00 - 0.19
2. Weak : 0.20 - 0.39
3. Moderate : 0.40 - 0.59
4. Strong : 0.60 - 0.79
5. Very strong : 0.80 - 1.00

8. Example
Image from : Lind, Douglas A., Marchal, William G., Wathen, Samuel A., 2021

9. ● Regression Analysis
Develop an equation that will allow us to estimate the
value of one variable based on the value of another.
● Least Square Principle
A mathematical procedure that uses the data to position a
line with the objective of minimizing the sum of the
squares of the vertical distances between the actual y
values and the predicted values of y.
Regression Analysis

10. Regression Analysis
Image from : Lind, Douglas A., Marchal, William G., Wathen, Samuel A., 2021

11. Regression Analysis
Image from : Lind, Douglas A., Marchal, William G., Wathen, Samuel A., 2021

12. Regression Analysis
Image from : Lind, Douglas A., Marchal, William G., Wathen, Samuel A., 2021

13. Regression Analysis
Image from : Lind, Douglas A., Marchal, William G., Wathen, Samuel A., 2021

14. Correlation Analysis & Regression Analysis

15. Correlation Analysis & Regression Analysis
● If the company has 100
employees, can we apply the
correlation and regression
equation?

16. Testing the Significance of
the Correlation Coefficient
01
13 - Correlation & Linear Regression 2
Testing the Significance of
the Regression Equation
02

17. ● If the company has 100
employees, can we apply the
correlation and regression
equation?
● We will use the concept of
inferential statistics.
Testing the Significance of the Correlation Coefficient

18. From the sample, the Sales Manager wants to know could
there be zero correlation in the population from which the
sample was selected?
Develop the Hypothesis:
● H0 : ρ = 0 → The correlation in the population is zero.
● H1 : ρ ≠ 0 → The correlation in the population is different
from zero.
Testing the Significance of the Correlation Coefficient

19. Testing the Significance of the Correlation Coefficient
Image from : Lind, Douglas A., Marchal, William G., Wathen, Samuel A., 2021

20. Known:
r = 0.8646
n = 15
Determine the Test Statistics:
Testing the Significance of the Correlation Coefficient

21. Determine the Critical Value:
df = n - 2 = 15 - 2 = 13
Testing the Significance of the Correlation Coefficient
Image from : Lind, Douglas A., Marchal, William G., Wathen, Samuel A., 2021

22. Determine the Critical Value:
Testing the Significance of the Correlation Coefficient
Image from : Lind, Douglas A., Marchal, William G., Wathen, Samuel A., 2021

23. Make Decision:
Test Statistics : 6.205088676
Critical Value : ±2.160
6.2051 > 2.160 → (+) Test statistics > (+) Critical value
Reject H0
Testing the Significance of the Correlation Coefficient

24. Interpretation:
With 𝛼 = 5%, there is correlation with respect to the number of
sales calls made and the number of copiers sold in the
population of salespeople.
Testing the Significance of the Correlation Coefficient

25. Testing the Significance of the Correlation Coefficient
Make Decision:
Test Statistics : 6.205088676
Check the Result from Data Analysis in GSheets / Excel:

26. How if the Sales Manager wants to know could there be a
positive correlation in the population from which the sample
was selected?
Testing the Significance of the Correlation Coefficient

27. Testing the Significance of
the Correlation Coefficient
01
13 - Correlation & Linear Regression 2
Testing the Significance of
the Regression Equation
02

28. ● Y’ = 19,98 + 0,2606 x
● This is the regression equation
of the sample.
● How about the regression
equation of the population?
Testing the Significance of the Regression Equation

29. ● Y’ = 19,98 + 0,2606 x
● We identified the intercept value
as a.
● We use “A” to represent the
population intercept.
Testing the Significance of the Intercept

30. Where:
● a = sample intercept
● A = population intercept
● sa = the standard error of the intercept estimate
Testing the Significance of the Intercept

31. Testing the Significance of the Intercept

32. the Sales Manager wants to know could the intercept in the
population is not 0 from which the sample was selected?
Develop the Hypothesis:
● H0 : A = 0 → The slope in the population is zero.
● H1 : A ≠ 0 → The slope in the population is different from
zero.
Testing the Significance of the Intercept

33. Known:
a = 19.98
sa = 4.38967553266198
Determine the Test Statistics:
Testing the Significance of the Intercept

34. Determine the Critical Value:
df = n - 2 = 15 - 2 = 13
Image from : Lind, Douglas A., Marchal, William G., Wathen, Samuel A., 2021
Testing the Significance of the Intercept

35. Make Decision:
Test Statistics : 4.551589258
Critical Value : ±2.160
4.552 > 2.160 → (+) Test statistics > (+) Critical value
Reject H0
Testing the Significance of the Intercept

36. Interpretation:
With 𝛼 = 5%, the intercept of the number of sales calls made
and the number of copiers sold in the population of
salespeople is significant.
Testing the Significance of the Intercept

37. ● Y’ = 19,98 + 0,2606 x
● We identified the slope
(kemiringan) value as b.
● We use “β” to represent the
population slope.
Testing the Significance of the Slope

38. Develop the Hypothesis:
● H0 : β = 0 → The slope in the population is zero.
The regression line is horizontal and there is no
relationship between the independent variable (X) and
dependent variable (Y).
● H1 : β ≠ 0 → The slope in the population is different from
zero.
Testing the Significance of the Slope

39. Testing the Significance of the Slope

40. Testing the Significance of the Slope

41. the Sales Manager wants to know could there be a positive
slope in the population from which the sample was selected?
Develop the Hypothesis:
● H0 : β <= 0 → The slope in the population is zero.
● H1 : β > 0 → The slope in the population is different from
zero.
Testing the Significance of the Slope

42. Known:
b = 0.260625
sb = 0.0420018171539133
Determine the Test Statistics:
Testing the Significance of the Slope

43. Determine the Critical Value:
df = n - 2 = 15 - 2 = 13
Image from : Lind, Douglas A., Marchal, William G., Wathen, Samuel A., 2021
Testing the Significance of the Slope

44. Make Decision:
Test Statistics : 6.205088676
Critical Value : 1.771
6.2051 > 1.771 → (+) Test statistics > (+) Critical value
Reject H0
Testing the Significance of the Slope

45. Interpretation:
With 𝛼 = 5%, the slope of the number of sales calls made and
the number of copiers sold in the population of salespeople is
positive / significant.
Testing the Significance of the Slope

46. Testing the Significance of the Slope & Intercept

47. Y’ = 19.98 + 0.2606 X
(Number of products sold) = 19.98 + 0.2606 (number of sales calls)
Is the regression equation is a good predictor?
Finding the exact outcome is practically impossible. Therefore, we
know the standard error of estimate.
Standard Error of Estimate is a measure of dispersion of the
observed values around the line of regression.
Standard Error of Estimate

48. Standard Error of Estimate

49. Standard Error of Estimate

50. The interval of estimated value of products sold (Y) could be
determined by calculating the upper and lower bound.
Interval Y’ = Y’ ± sy.x
Standard Error of Estimate

51. Standard Error of Estimate

52. Interval of the Intercept & Slope

53. The proportion of the total variation in the dependent variable Y
that is explained by the variation in the independent variable X.
Symbol : r^2 (R Square)
The Coefficient of Determination

54. The Coefficient of Determination

55. r square = 0.7475
Interpretation:
74.75% variance of products sold has been explained by sales
calls. The other 25.25% could be explained by other factors.
The Coefficient of Determination

56. https://docs.google.com/spreadsheets/d/1Pj0mP5M6sJbnMFU75nHSKypt9V
UZYa_qjCIQYRX8sAo/edit?usp=sharing
Exercise

57. References
Lind, Douglas A., Marchal, William G., Wathen, Samuel A.. (2021). Statistical techniques in business & economics

58. Present Form - System
Pada bagian komentar silahkan
isi:
1. Hal yang saya pelajari hari ini.
2.Hal menarik dari perkuliahan
hari ini.
3.Hal yang masih ingin saya cari
tahu setelah perkuliahan ini.
4.Saran.

59. CREDITS: This presentation template was created by Slidesgo, and
includes icons by Flaticon, and infographics & images by Freepik
Thanks!
Any questions?
Please keep this slide for attribution