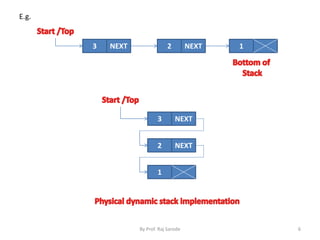
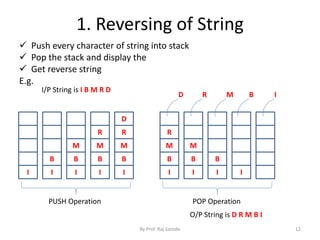
The document discusses stacks and their implementation and applications. It defines a stack as a linear data structure for temporary storage where elements can only be inserted or deleted from one end, called the top. Stacks follow the LIFO (last in, first out) principle. Stacks have two main operations - push, which inserts an element, and pop, which removes the top element. Stacks can be implemented using arrays or linked lists. Common applications of stacks include reversing strings, checking matching parentheses, and converting infix, postfix, and prefix expressions.

1. Chapter 4
Stack

2. Stack
“Stack is a linear data structure used for
temporary storage where elements can be
inserted or deleted at only one end called
TOP of the stack”
LIFO – Last in First Out
e.g. Stack of Subject Book
By Prof. Raj Sarode 2

3. Stack
WT
DS DS
OOAD
WT
DS
DCCN
OOAD
WT
DS
E.g.
suppose Four Books like DS, WT, OOAD, DCCN are we entered into Stack
By Prof. Raj Sarode 3
TOP
TOP
TOP
TOP
E
M
P
T
Y
TOP

4. Implementation or Representation of Stack
1 Static / sequential / array representation
 In this case of array, stack is also collection of
homogeneous elements .
 Therefore stack can be easily implemented
using array.
 Two operation : PUSH & POP
 Element stored from stack[0] to stack[TOP]
 Stack[0] ->Bottom of STACK
 Stack [TOP]-> Top of STACK
 TOP =-1 It indicate Stack is Empty.
By Prof. Raj Sarode 4

5. 2 Dynamic / pointer/ linked Representation
 In Dynamic or linked representation stack is
collection of nodes. Where each node is divided in to
two parts
INFO NEXT
Top of stack is represented by start pointer of linked
list
 If START =NULL , it shows that stack is empty & TOP =
NULL
 Last node Next part contain NULL Value, it Indicate
bottom of stack
By Prof. Raj Sarode 5
Store Data <-
Structure of Node
->Point to next Node

6. 3 NEXT 2 NEXT 1
E.g.
3 NEXT
2 NEXT
1
By Prof. Raj Sarode 6

7. Stack Operation
1. PUSH Operation
 Used to insert element into Stack
e.g.
2
1
0
Top=-1
Empty Stack
A
2
1
0
Insert A
Top=0
B
A
2
1
0
Insert B
Top=1
C
B
A
2
1
0
Insert C
Top=2
Top->
Top->
Top->
 Each time new element is inserted into stack,
the value of Top is incremented by one
 Top=2 i.e. MAX-1. It shows stack is Overflow
By Prof. Raj Sarode 7

8. Algorithm 1
Push(stack, MAX, Top, Ele)
1. Check for Overflow
a. If Top=MAX-1 then
b. Print “overflow” & return
Else
a. Top = Top+1 //Increment Top by One
b. Stack[Top]=Ele //insert Element at new Location
End if
2. Return.
By Prof. Raj Sarode 8

9. Stack Operation
2. POP Operation
 Used to Delete element From Stack
e.g.
2
1
0
A is Removed
Top=-1
Stack is Empty
A
2
1
0
B is Removed
Top=0
B
A
2
1
0
C is Removed
Top=1
C
B
A
2
1
0
Top=2
Top->
Top->
Top->
 In POP Last inserted element is Deleted First [LIFO]
 After deleting element value of top is decreased by one
 When all elements from stack are removed (i.e. empty stack) we
cannot removed anything from stack. This condition is called
“Underflow” By Prof. Raj Sarode 9

10. Algorithm 2
POP(stack, MAX, Top, Ele)
1. Check for Underflow
a. If Top=-1 then
b. Print “underflow” & return
Else
a. Ele=Stack[Top] //delete element from stack
b. Top = Top-1 //decrement Top by One
End if
2. Return.
By Prof. Raj Sarode 10

11. Application of Stack
• Reversing of String
• Matching Parenthesis
• Conversion of Expression
• Evaluation of Expression
By Prof. Raj Sarode 11

12. 1. Reversing of String
 Push every character of string into stack
 Pop the stack and display the
 Get reverse string
E.g.
R
M
B
M
B
B
By Prof. Raj Sarode 12
B
I I
M
B
I
R
M
B
I
D
R
M
B
I
PUSH Operation
I
D
I
R
I
M
I
B I
POP Operation
O/P String is D R M B I
I/P String is I B M R D

13. 2. Matching parenthesis
1. Initially take an empty stack
2. Scan the symbol of expression from left to right
3. If the symbol is left parenthesis the push into stack.
4. If the symbol is right parenthesis
a. if stack is empty
b. print “right parenthesis are more than left parenthesis.”
else
a. pop element from stack
b. if pop parenthesis !=Element
c. Print “Mismatched parenthesis.”
5. After scanning all the symbol
a. If the stack is empty
Print “parenthesis are equal: valid”
else
Print “left parenthesis are more than right parenthesis.”
By Prof. Raj Sarode 13

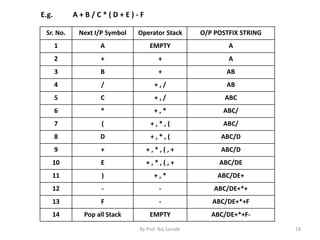
14. By Prof. Raj Sarode 14
E.g. (A + B ) * ( C – D )
Sr. No. Next I/P Symbol Stack O/P
1 ( (
2 A (
3 + (
4 ) EMPTY [pop 1 left Parenthesis]
5 * EMPTY
6 ( (
7 C (
8 - (
9 D ( [pop 1 left Parenthesis]
10 ) EMPTY Valid Expression

15. 3. Conversion of Expression
1. Infix to Postfix e.g. A+B -> AB+
2. Infix to Prefix e.g. A+B -> +AB
3. Postfix to Infix e.g. AB+ -> A+B
4. Postfix to Prefix e.g. AB+ -> +AB
5. Prefix to Infix e.g. +AB -> A+B
6. Prefix to Postfix e.g. +AB -> AB+
By Prof. Raj Sarode 15

16. Expressions
Expression is of Three types
1. Infix Expression
A + B
2. Postfix Expression
A B +
3. Prefix Expression
+ A B
Note: Priority of operators (, ), ^, *, /, +, -.
# indicate end of expression.
By Prof. Raj Sarode 16

17. Infix to Postfix Conversion
Algorithm
1. Read the infix expression from left to right one character at a time.
2. Repeat step 3
3. Read symbol
a. If symbol is operand put into postfix string
b. If symbol is left parenthesis push into stack
c. If right parenthesis, pop stack of TOP until left parenthesis occur and
make postfix expression
d. If operator then
I. If operator has same of less precedence then operators available at
top of stack, then pop all such operators and form postfix string
II. Push scanned /incoming operator to the stack
4. Until last of string encountered
5. Pop all the element from stack to make stack empty
By Prof. Raj Sarode 17

18. E.g. A + B / C * ( D + E ) - F
Sr. No. Next I/P Symbol Operator Stack O/P POSTFIX STRING
1 A EMPTY A
2 + + A
3 B + AB
4 / + , / AB
5 C + , / ABC
6 * + , * ABC/
7 ( + , * , ( ABC/
8 D + , * , ( ABC/D
9 + + , * , ( , + ABC/D
10 E + , * , ( , + ABC/DE
11 ) + , * ABC/DE+
12 - - ABC/DE+*+
13 F - ABC/DE+*+F
14 Pop all Stack EMPTY ABC/DE+*+F-
By Prof. Raj Sarode 18

19. Infix to Prefix Conversion
Note: for converting infix exp. To prefix exp. It requires two stack 1. operator stack 2. operand stack.
Algorithm
1. Read the infix expression from left to right one character at a time.
2. Repeat step 3
3. Read symbol
a. If symbol is operand put into operand stack
b. If symbol is left parenthesis push into operator stack
c. If right parenthesis, pop two operand and one operator and push in operand
stack until left parenthesis occur.
d. If scan symbol is operator then
I. If operator has same of less precedence then operator available on top of
operator stack, then pop one operator and two operand form prefix
expression & push into operand stack
4. Repeat Until end of expression.
5. Pop all the remaining operator and corresponding operand and form prefix
expression
6. Exit.
By Prof. Raj Sarode 19

20. By Prof. Raj Sarode 20
E.g. A + B / C – D * E + F
Sr. No. Next I/P Symbol Operator Stack Operand Stack
1 A EMPTY A
2 + + A
3 B + A , B
4 / + , / A , B
5 C + , / A , B , C
6 - + A , / B C
7 - - + A / B C
8 D - + A / B C , D
9 * - , * + A / B C , D
10 E - , * + A / B C , D , E
11 + - + A / B C , * D E
12 + + - + A / B C * D E
13 F + - + A / B C * D E , F
14 END OF I/P POP ALL STACK + - + A / B C * D E F FINAL O/P

21. Postfix to Infix Conversion
Algorithm
Note: for converting postfix expression to infix it require operand stack to store the operands
1. Read the Postfix expression from left to right one character at a time.
2. If it is operand push into operand stack.
3. If it is operator
a. Pop two operand from stack
b. Form infix expression and push into operand stack.
4. If expression is not end go to step One
5. Pop operand stack and display.
6. Exit
By Prof. Raj Sarode 21

22. By Prof. Raj Sarode 22
E.g. A B + C D - /
Sr. No. Next I/P Symbol Operand Stack Infix Expression
1 A A
2 B A, B
3 + A + B A + B
4 C A + B, C
5 D A + B, C , D
6 - A + B, C – D C - D
7 / A + B / C – D A + B / C – D FINAL O/P

23. Postfix to Prefix Conversion
Algorithm
Note: for converting postfix expression to prefix it require operand stack to store the operands
1. Read the Postfix expression from left to right one character at a time.
2. If it is operand push into operand stack.
3. If it is operator
a. Pop two operand from stack
b. Form prefix expression and push into operand stack.
4. If expression is not end go to step One
5. Pop operand stack and display.
6. Exit
By Prof. Raj Sarode 23

24. By Prof. Raj Sarode 24
E.g. A B + C * D /
Sr. No. Next I/P Symbol Operand Stack Prefix Expression
1 A A
2 B A , B
3 + + A B + A B
4 C + A B, C
5 * * + A B C * + A B C
6 D * + A B C , D
7 / / * + A B C D / * + A B C D FINAL O/P

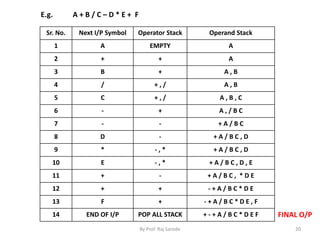
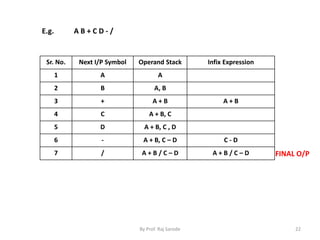
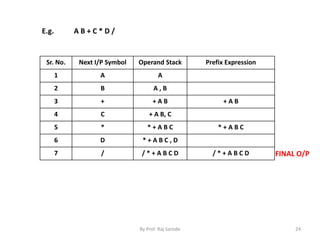
25. Prefix to Infix Conversion
Algorithm
Note: for converting prefix expression to infix it require one stack to store the operator as well as
operands
1. Read the prefix expression from left to right one character at a time.
2. If it is operator push into stack.
3. If it is operand
while (operand (stack[TOP])
{ operand1 = pop();
operator = pop();
expression=(operand1, operator, symbol)
symbol=expression; }
4. Push symbol into stack
5. If prefix string is not end go to step one
6. POP stack & Display it
7. Exit
By Prof. Raj Sarode 25

26. By Prof. Raj Sarode 26
E.g. * + A B – C D
Sr. No. Next I/P Symbol Stack Infix Expression
1 * *
2 + * , +
3 A * , + , A
4 B * , A + B A + B
5 - * , A + B , -
6 C * , A + B , - , D
7 D * , A + B , C – D C – D
8 C – D A + B * C – D A + B * C – D FINAL O/P

27. Prefix to Postfix Conversion
Algorithm
Note: for converting prefix expression to Postfix it require one stack to store the operator as well
as operands
1. Read the prefix expression from left to right one character at a time.
2. If it is operator push into stack.
3. If it is operand
while (operand (stack[TOP])
{ operand1 = pop();
operator = pop();
expression=(operand1, symbol, operator)
symbol=expression; }
4. Push symbol into stack
5. If prefix string is not end go to step one
6. POP stack & Display it
7. Exit
By Prof. Raj Sarode 27

28. By Prof. Raj Sarode 28
E.g. / * + A B C D
Sr. No. Next I/P Symbol Stack Postfix Expression
1 / /
2 * / , *
3 + / , * , +
4 A / , * , + , A
5 B / , * , A B + A B +
6 C / , A B + C * A B + C *
7 D A B + C * D / A B + C * D / FIN`AL O/P

29. /*program For stack operation */
By Prof. Raj Sarode 29
#include<iostream.h>
#include<conio.h>
#include<stdlib.h>
class stack
{
int stk[5];
int top;
public:
stack()
{ top=-1; }
void push(int x)
{ if(top > 4)
{ cout <<"stack over flow";
return;
}
stk[++top]=x;
cout <<"inserted" <<x;
}
void pop()
{ if(top <0)
{ cout <<"stack under flow";
return;
}
cout <<"deleted" <<stk[top--]; }
void display()
{ if(top<0)
{ cout <<" stack empty";
return;
} for(int i=top;i>=0;i--)
cout <<stk[i] <<" ";
} };
main()
{ int ch;
stack st;
while(1)
{ cout <<"n1.push 2.pop 3.display
4.exitnEnter ur choice";
cin >> ch;
switch(ch)
{ case 1: cout <<"enter the element";
cin >> ch;
st.push(ch);
break;
case 2: st.pop(); break;
case 3: st.display();break;
case 4: exit(0);
} }
return (0); }

30. /*program For Reverse String */
By Prof. Raj Sarode 30
#include<iostream.h>
#include<conio.h>
#include<stdlib.h>
# define MAX 10
class stack
{ char stk[MAX];
int top;
public:
stack()
{ top=-1; }
void push()
{ int n,i;
cout<<"Enter the size of string";
cin>>n;
if(n>MAX)
{ cout<<"out of size";
} else
{ for(i=0;i<n;i++)
cin>>stk[++top];
}
}
void reverse()
{ if(top<0)
{ cout <<" stack empty";
return;
} for(int i=top;i>=0;i--)
cout <<stk[i] <<" ";
} };
main()
{ int ch;
clrscr();
stack st;
while(1)
{ cout <<"n1.push 2.reverse 3.exitn Enter ur
choice";
cin >> ch;
switch(ch)
{
case 1: st.push();break;
case 2: st.reverse();break;
case 3: exit(0);
} }
return (0); }

31. Thank You
By Prof. Raj Sarode 31