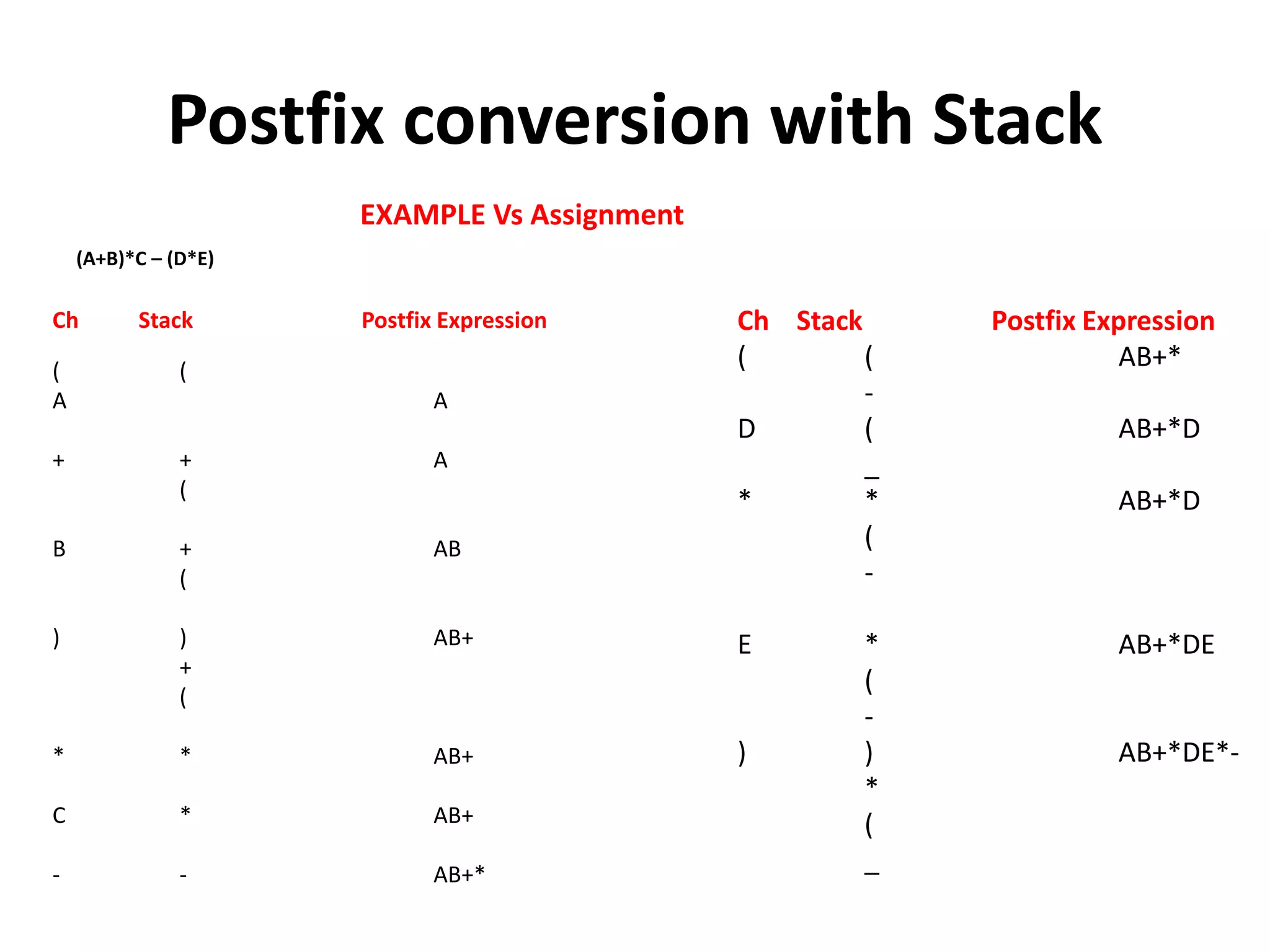
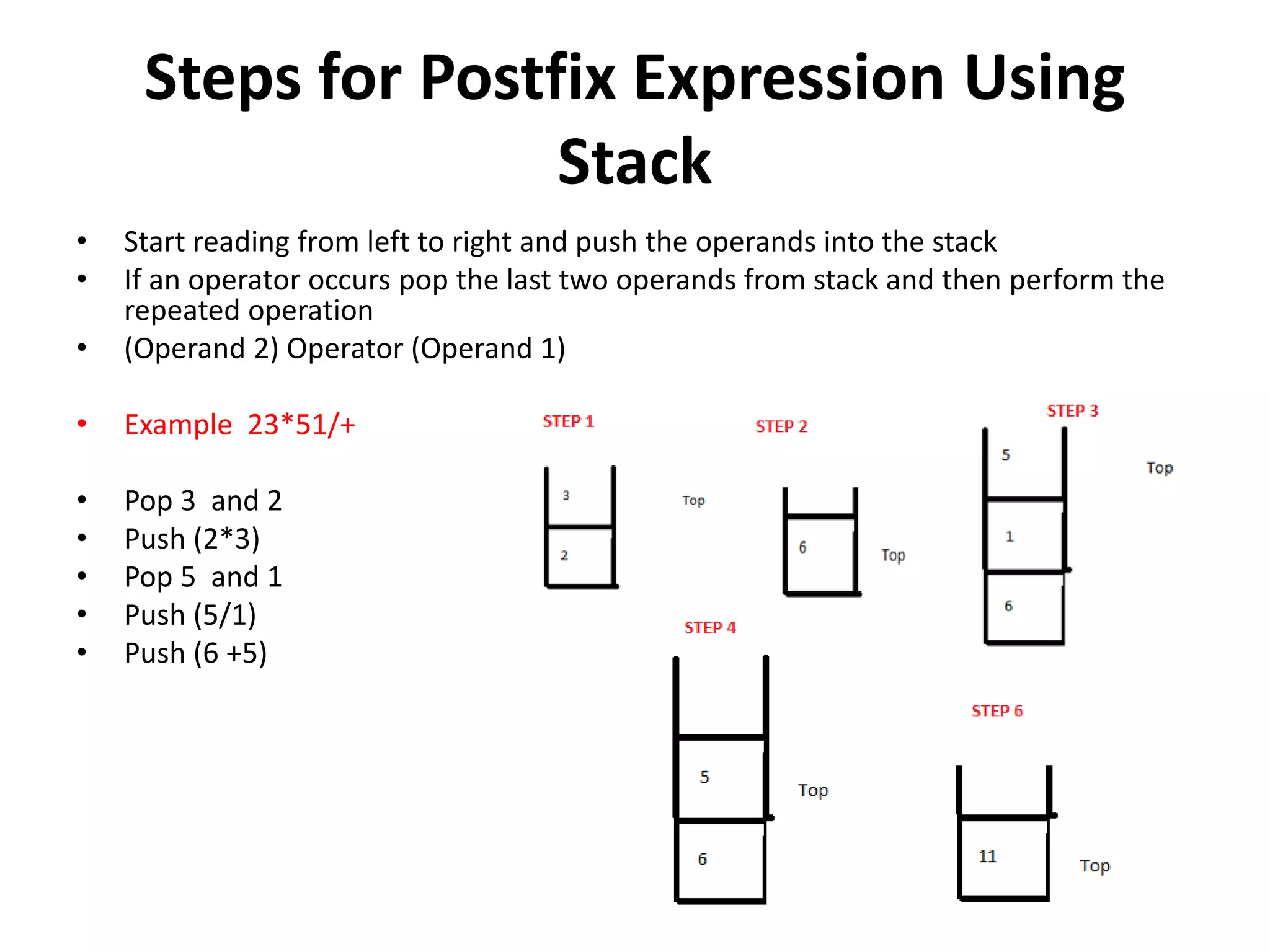
The document discusses evaluation of expressions and the conversion between infix and postfix notations. It provides examples of: 1) Evaluating expressions using the order of operations and precedence of operators. Scenarios are worked through step-by-step. 2) Converting infix notation expressions to equivalent postfix notation expressions using a stack-based algorithm. 3) Evaluating postfix notation expressions using a stack to pop operands and operators in order.

1. Evaluation of Expression
Dr. R. Khanchana
Assistant Professor
Department of Computer Science
Sri Ramakrishna College of Arts and Science for
Women

2. Evaluation of Expression
• An expression is made up of operands,
operators and delimiters.
• Operands - A,B,C,D,E (these are all one letter variables)
• Operators **,+,*,-, /, =
• A = 4, B = C = 2, D = E = 3
• Output ?

3. Evaluation of Expression

4. Basic Operator Types
• Basic arithmetic operators:
– Plus, minus, times, divide, and exponentiation
• (+,-,*,/,**)
• Other arithmetic operators
– Unary plus, unary minus and mod, ceil, and floor.
• Relational operators
• Relational operators is one of the two
constants: true or false (Boolean)

5. Priority of arithmetic, Boolean and
relational operators

6. Precedence of Operator
• Operator Associativity
• (),{},[]
• ^ - Right to Left
• * / - Left to Right
• + - - Left to Right

7. Order of Evaluation
Scenario 1
• A = 4, B = C = 2, D = E = 3,
• 4/(2 ** 2) + (3 * 3) - (4 * 2)
• = (4/4) + 9 - 8
• = 2.
Scenario 2
• (4/2) ** (2 + 3) * (3 - 4) * 2
• = (4/2) ** 5* -1 * 2
• = (2**5)* -2
• = 32* -2
• = -64.

8. Infix & Postfix Notation
• If e is an expression with operators and
operands, the conventional way of writing e is
called infix, because the operators come in-
between the operands.
• The postfix form of an expression calls for
each operator to appear after its operands.
• Example
– Infix: A * B/C
– Postfix: AB * C/

9. Infix to Postfix Conversion
It is simple to describe an algorithm for producing postfix from infix:
1) Fully parenthesize the expression
2) Move all operators so that they replace their corresponding right
parentheses
3) Delete all parentheses.
Example : A/B ** C + D * E - A * C when fully parenthesized yields
The arrows point from an operator to its corresponding right
parenthesis. Performing steps 2 and 3 gives
ABC ** / DE * + AC * -

10. Infix & Postfix Expression
• Infix: A/B ** C + D * E - A * C
• Postfix: ABC ** /DE * + AC * -
Operation Postfix
--------- -------
T1 = B **C AT1/DE * + AC * -
T2 = A/T1 T2DE * + AC * -
T3 = D * E T2T3 + AC * -
T4 = T2 + T3 T4AC * -
T5 = A * C T4T5 -
T6 = T4 - T5 T6

11. Steps for Postfix Expression Using
Stack
• Start reading from left to right and push the operands into the stack
• If an operator occurs pop the last two operands from stack and then perform the
repeated operation
• (Operand 2) Operator (Operand 1)
• Example 23*51/+
• Pop 3 and 2
• Push (2*3)
• Pop 5 and 1
• Push (5/1)
• Push (6 +5)

12. Procedure -Expression Evaluation

13. STACK Implementation
• A + B * C to yield ABC * + our algorithm
should perform the following sequence of
stacking

14. STACK Implementation
• Animated Video
• https://www.youtube.com/watch?v=TeM6Ddv
SxvQ

15. Assignment
• Another example, A * (B + C) * D has the
postfix form ABC + * D *

16. Assignment Results
A * (B + C) *

17. Priorities of Operators for Producing
Postfix

18. Postfix conversion with Stack
EXAMPLE 1

19. Postfix conversion with Stack
EXAMPLE 2
-
-
-

20. Postfix conversion with Stack
(A+B)*C – (D*E)
Ch Stack Postfix Expression
( (
A A
+ + A
(
B + AB
(
) ) AB+
+
(
* * AB+
C * AB+
- - AB+*
Ch Stack Postfix Expression
( ( AB+*
-
D ( AB+*D
_
* * AB+*D
(
-
E * AB+*DE
(
-
) ) AB+*DE*-
*
(
_
EXAMPLE Vs Assignment

21. Procedure Postfix

22. Quiz
• https://quizizz.com/admin/quiz/5f14103a219
aa5001b718cf1