POMDPの話。

1. 確率ロボティクスと移動ロボットの行動生成
第9回
上田隆一

2. 本日の内容
• POMDP
Oct. 7, 2015 確率ロボティクスと移動ロボットの行動生成 2

3. POMDP
• 部分観測マルコフ決定過程
• 状態が自明でない場合のマルコフ決定過程
– センサ情報から得られるが、部分的
• ほぼ、自律型ロボットの問題に相当
• 他者がいるとさらに問題が難しくなるが、
POMDPでは考えない/扱えない
Oct. 7, 2015 確率ロボティクスと移動ロボットの行動生成 3

4. 定式化
• 状態が直接観測できず、観測から間接的に分かる
Oct. 7, 2015 確率ロボティクスと移動ロボットの行動生成 4

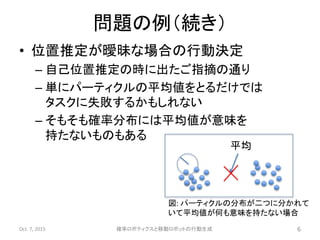
5. 問題の例
• スイカ割り
– 自分とスイカの相対姿勢がはっきり分からない
– 他者からの情報で
• スイカ割り（目隠しをしなくても）
– 実は目隠しをしなくても相対姿勢が絶対的に
分かっているわけではない
– 単なる程度の問題で、実世界では常に不確かさが伴う
– ロボットにやらせると大変でしょう？
• 枠組みや問題の複雑さを知っておくことが設計の際に重要
Oct. 7, 2015 確率ロボティクスと移動ロボットの行動生成 5

6. • 位置推定が曖昧な場合の行動決定
– 自己位置推定の時に出たご指摘の通り
– 単にパーティクルの平均値をとるだけでは
タスクに失敗するかもしれない
– そもそも確率分布には平均値が意味を
持たないものもある
Oct. 7, 2015 確率ロボティクスと移動ロボットの行動生成 6
平均
図: パーティクルの分布が二つに分かれて
いて平均値が何も意味を持たない場合
問題の例（続き）

7. • その他人間の場合
– 人生の中のPOMDPを見つけてみましょう
（丸投げ）
Oct. 7, 2015 確率ロボティクスと移動ロボットの行動生成 7
問題の例（続き）

8. 確率的な自己位置推定との関係
• ロボットがbelから行動決定
– 観測→信念
• 状態の上で定義された方策ではなく、
belの上で定義された方策となる
– bel: 信念
– 「信念に対する方策」
• どうやって求めるか？
• そもそも求められるのか？
Oct. 7, 2015 確率ロボティクスと移動ロボットの行動生成 8

9. 問題の大きさ
• 状態が100個、行動が2種類の場合
• MDP
– 方策のパターンは2^100通り
– 価値反復を使うと
O(状態数・行動数・タスクの長さ)
で方策を1個選ぶことができる
• POMDP
– belは100個の上で定義される関数
• 無限に存在
– 無限にあるものに対する方策のパターンは無限
Oct. 7, 2015 確率ロボティクスと移動ロボットの行動生成 9

10. POMDPとハンドコーディング
• 例えば、パーティクルの分布から
移動ロボットの行動を決めるコードを書いてみましょう
– 例えば脱輪したり縁石に乗り上げたりしないで、
できるだけ早く角を曲がる場合を考えてみましょう
– （たいていの場合）ほぼ無限に場合分けできる
• 疲れる
– そもそも「無理」
という場合も
• 豊富な研究テーマ
Oct. 7, 2015 確率ロボティクスと移動ロボットの行動生成 10

11. 角を曲がるための研究テーマの例
• なんとなくセンサを乗っけて対処しようとしたり、
コーディングでごまかすのはもったいない
– 問題をきっちり定式化することで、研究として扱える
– 実はロボットで扱う一般的（そして深刻）な問題になっている
• 曖昧さを考慮した行動の選択
– 今日の後半はこの話だけ
• 他にも考えられる（次のページ）
Oct. 7, 2015 確率ロボティクスと移動ロボットの行動生成 11

12. • 観測戦略
– 位置が分からないような状況で角に
突っ込まないために能動的に観測
• ロボットの形状やセンサの配置を考える
– 角に突っ込んでも壊れない
– 形状が情報処理の負荷を下げる（身体性とも関連）
• 確率分布の表現
– 普通のパーティクルフィルタは一箇所にパーティクルが
集まりがち
Oct. 7, 2015 確率ロボティクスと移動ロボットの行動生成 12

13. 信念からの方策の求め方
• 無限に存在するbel（信念状態）に対してどのように
行動を対応づけて方策を作るか？
• ここでは以下の二つについて扱う
（他に探索等の手法）
– 方法1:
• 信念状態を有限個に分類して行動を割り付け
• MDPのように学習や価値反復で
– 方法2:
• 事前にMDPの問題を解いて再利用
Oct. 7, 2015 確率ロボティクスと移動ロボットの行動生成 13

14. 方法1（AMDPと呼ばれる手法群）
• 信念の数を有限個に近似
• 例[Roy 99]
– 距離センサを持つ移動ロボットのナビゲーション問題
– 4次元の状態空間を作る
• xyqを離散化
• 位置推定の分布がどれだけ曖昧か数値化して離散化
• 状態遷移はなんとか計算
– 得られる行動
• 自己位置が分からなくならないように壁沿いを走る
Oct. 7, 2015 確率ロボティクスと移動ロボットの行動生成 14

15. 方法2（QMDP, 他）
• MDPの計算結果を利用する
– 状態遷移の法則性が分かっているが、ロボットが
自分の状態を完全に分からない場合に使える
• 例[Littman95]
– 確率密度関数belと価値関数Vから価値の
期待値を計算
Oct. 7, 2015 確率ロボティクスと移動ロボットの行動生成 15

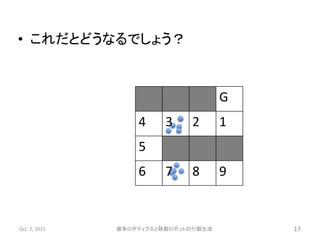
16. • 例
– 下のような碁盤の目の環境を考える
– 1マスが1状態
– 行動は上下左右
– 同じ重みを持ったパーティクル10個が分布
– タスクはゴール（G）に
最短歩数で到達すること
– 数字はコスト
– 灰色のところに入ろうとすると
戻される
– 問題
• 一番「価値の高い」行動は？
Oct. 7, 2015 確率ロボティクスと移動ロボットの行動生成 16
3 2 1 G
4 3 2 1
5 4
6 5 6 7

17. • これだとどうなるでしょう？
Oct. 7, 2015 確率ロボティクスと移動ロボットの行動生成 17
G
4 3 2 1
5
6 7 8 9

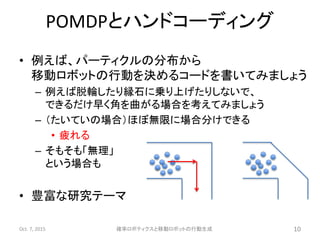
18. probabilistic flow control[ueda2015]
• 手前味噌ですが・・・
• 期待値計算において
「重み = パーティクルの重み/価値」とする
– ゴールに近いパーティクルが
行動決定に大きな影響を与える
• 投機的な行動が生成され、
ロボットがゴールを探すようになる
– ただしこれでもデッドロックは
発生する
• 問題を完全には解いていないので
• 研究は続く・・・
Oct. 7, 2015 確率ロボティクスと移動ロボットの行動生成 18
G
4 3 2 1
5
6 7 8 9
重み1/3
重み1/7

19. 次回
• POMDPの一つの解としてPFCの実機実装を扱う
• その後、PFCとは違う論文を読む
– 偏るので
Oct. 7, 2015 確率ロボティクスと移動ロボットの行動生成 19