Download as PDF, PPTX
機械学習入門の入門
- 1. 機械学習 machine-learning • 教師なし学習 unsupervised learning – 階層的クラスタリング hierarchical clustering • 最短距離法 Single-linkage • 最長距離法 Complete-linkage • 平均法 Average method • 重心法 Centroid method – 主成分分析 principal component analysis; PCA • 教師あり学習 supervised learning • 決定木 decision tree • ランダムフォレスト random forest • サポートベクトルマシン support vector machine (SVM) • ロジスティック回帰 logis@c regression • 線形判別分析 linear discriminant analysis (LDA) • 深層学習 deep learning 1
- 2.
- 3. 教師あり高次元ベクトルデータ • 化合物データ 白＝活性あり、黒＝活性なし • 遺伝子発現データなどと思ってくれても OKです。 • 簡単のため、２次元の整数で取り扱える データにしていますが、実際は高次元の 実数で取り扱います。 • 左のような観測データがあるとき、「？」 の場所の化合物が白か黒か予測したい。 3 ？
- 4.
- 5.
- 6.
- 7. 白か黒か予測する決定木（質問は２回までの場合） 7 X > 6 Yes Black: 1 White: 15 No Y < 3 Black: 28 White: 2 Black: 3 White: 15 START 白と予測 黒と予測 白と予測 黒と予測 本当は白 30 2 本当は黒 4 28 正解率(accuracy) = (30 + 28) / (30 + 2 + 4 + 28) = 0.906 白と予測 Yes No
- 8.
- 9. 観測できている範囲内でベストの予測を試みます。 9 ？ X < 1 Yes Black: 0 White: 2 No Y < 2 Black: 6 White: 2 Black: 1 White: 3 START 白と予測 黒と予測 白と予測 Yes No 白と予測 黒と予測 本当は白 5 2 本当は黒 1 6 見かけ上の正解率(accuracy) = (5 + 6) / (5 + 2 + 1 + 6) = 0.785 「？」は黒と予測。
- 10. 10 X < 1 Yes Black: 4 White: 4 No Y < 2 Black: 26 White: 16 Black: 2 White: 12 START 白と予測 黒と予測 白と予測 黒と予測 本当は白 16 16 本当は黒 6 26 真の正解率(accuracy) = (16 + 26) / (16 + 16 + 6 + 26) = 0.656 「？」の予測はハズレ 白と予測 Yes No 真の予測性能は、知る由も無い 見かけ上の正解率(accuracy) = (5 + 6) / (5 + 2 + 1 + 6) = 0.785 「？」は黒と予測。
- 11. 過学習 overfi^ng テスト問題だけ解けるようヤマを張った学習をしたせいで、現実の問題に対応する能 力が落ちること 11 適度な学習 過学習 予測 白 予測 黒 本当 白 6 1 本当 黒 2 5 予測 白 予測 黒 本当 白 30 2 本当 黒 4 28 予測 白 予測 黒 本当 白 7 0 本当 黒 0 7 予測 白 予測 黒 本当 白 25 6 本当 黒 5 27 黒 白 白 白 白 白 黒 黒 見かけ上の Accuracy = (6+5)/(6+1+2+5) = 0.79 真の Accuracy = (30+28)/(30+2+4+28) = 0.91 見かけ上の Accuracy = (7+7) / (7+0+0+7) = 1.0 真の Accuracy = (25+27)/(25+5+5+27) = 0.84
- 12. 交差検定 cross valida@on • 予測モデルの性能評価に用いる。 • 本当は答えの分かっている問題を「training data」と「test data」に分割し、training dataだけを使って予測モデルを構築し、test data の予測をし、答え合わせをする ことで、予測モデルの性能を見積もる。 12 本当は白黒分かっている問題 ４分割交差検定：ランダムに1/4 を選択して test data （グレー）とし、残りの 3/4 からグレーの本当 の色を予測する。それを４回繰り返す。
- 13. 予測モデルの評価方法いろいろ • Accuracy = (TP + TN) / (TP + FN + FP + TN) – 正解率。予測結果全体と、答えがどれぐらい一致しているかを判断する指標。 • Precision = TP / (TP + FP) – 適合率。予測を正と判断した中で、答えも正である割合。薬の設計などでは 一般に、Precisionが高い予測モデルが良しとされる。 • Recall = TP / (TP + FN) – 再現率、回収率ともいう。答えが正の中で、予測が正とされた割合。病気の 診断などでは一般に、Recallが高い予測モデルが良しとされる。 • F-measure = 2 x Precision x Recall / (Precision + Recall) – F値。PresicionとRecallの調和平均。一般にPrecisionとRecallは逆相関の関係 にあるので、バランスの良い予測をするためにF値を考えることがある。 • 「精度」という言葉はAccuracyの意味だったりPrecisionの意味だったり曖 昧なので、使用には注意されたい。 13 活性ありと予測 活性なしと予測 活性あり（陽性） True Posi@ve (TP) False Nega@ve (FN) 活性なし（陰性） False Posi@ve (FP) True Nega@ve (TN)
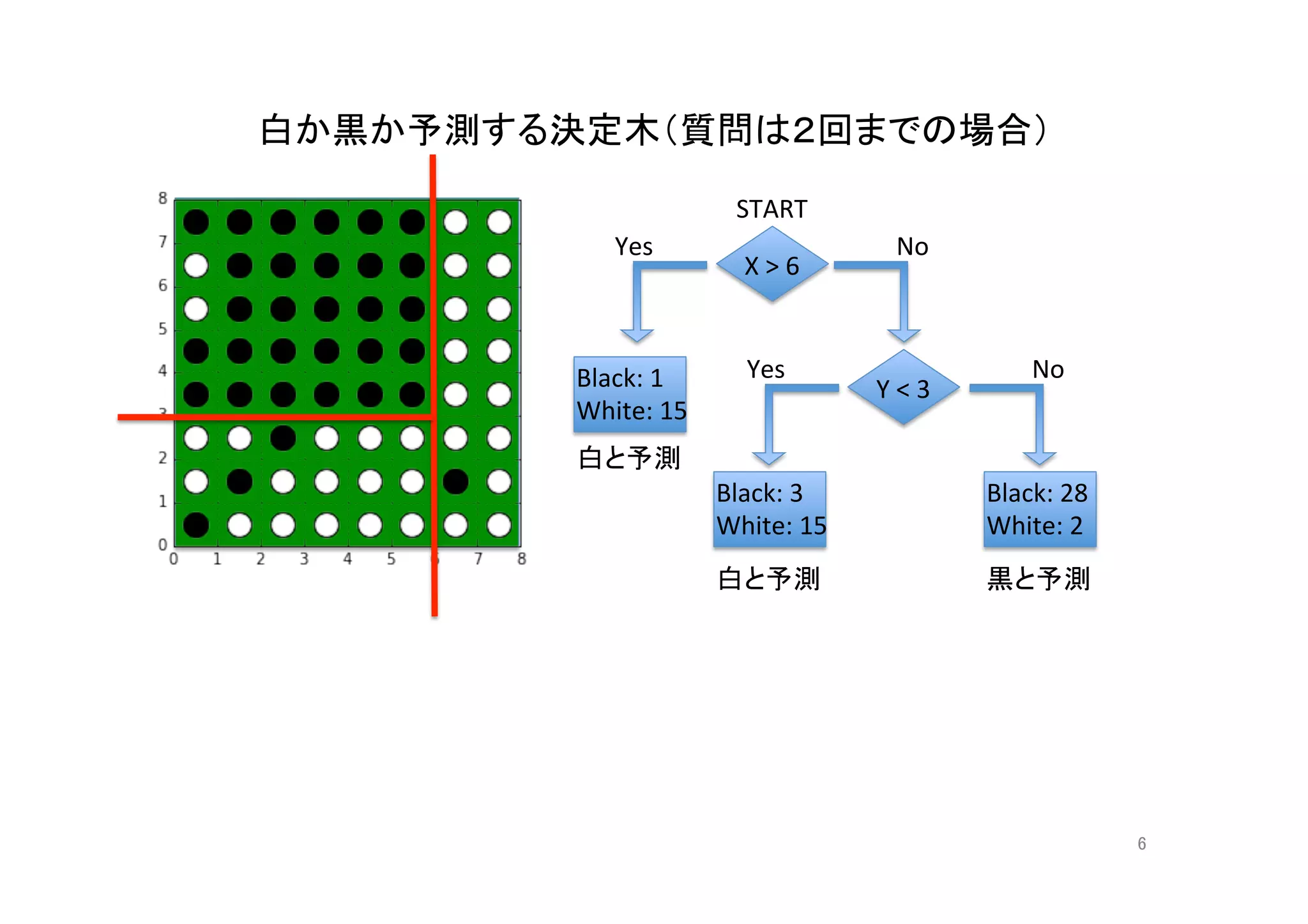
- 14. 決定木（質問は３回まで）の ４分割交差検定 4-fold cross valida@on 14 答え 白 白 白 白 白 白 白 白 白 白 白 黒 黒 黒 黒 黒 予測 白 予測 黒 本当 白 1 1 本当 黒 2 0 予測 白 予測 黒 本当 白 2 0 本当 黒 0 2 予測 白 予測 黒 本当 白 2 0 本当 黒 2 0 予測 白 予測 黒 本当 白 2 0 本当 黒 0 2 Accuracy = (1+0)/4 = 0.25 Precision = 1/(1+2) = 0.33 Recall = 1/(1+1) = 0.50 F-measure = 0.40 Accuracy = (2+2)/4 = 1.0 Precision = 2/(2+0) = 1.0 Recall = 2/(2+0) = 1.0 F-measure = 1.0 Accuracy = (2+0)/4 = 0.50 Precision = 2/(2+2) = 0.50 Recall = 2/(2+0) = 1.0 F-measure = 0.67 Accuracy = (2+2)/4 = 1.0 Precision = 2/(2+0) = 1.0 Recall = 2/(2+0) = 1.0 F-measure = 1.0 Accuracy = 0.6875 Precision = 0.71 Recall = 0.88 F-measure = 0.77 予測モデルの 平均性能
- 15.
- 16.
- 17. 教師あり高次元ベクトルデータの機械学習の解析例 17 青丸と赤丸に分かれる高次元 データを • Nearest Neighbor法 • 線形SVM • RBFカーネルSVM • 決定木 • ランダムフォレスト • Adaboost • Naive Bayes • 線形判別分析 • 二次判別分析 で学習し、その結果をPCAで二 次元空間上にプロットした図を 示す。色の付いたエリアがそ の予測結果で、右下の数字が Accuracy。様々な機械学習法 が開発されているが、それぞ れ得意な問題と苦手な問題が ある。
- 18. 教師あり高次元ベクトルデータの機械学習の解析例 18 青丸と赤丸に分かれる高次元 データを • Nearest Neighbor法 • 線形SVM • RBFカーネルSVM • 決定木 • ランダムフォレスト • Adaboost • Naive Bayes • 線形判別分析 • 二次判別分析 で学習し、その結果をPCAで二 次元空間上にプロットした図を 示す。色の付いたエリアがそ の予測結果で、右下の数字が Accuracy。様々な機械学習法 が開発されているが、それぞ れ得意な問題と苦手な問題が ある。
- 19. 教師あり高次元ベクトルデータの機械学習の解析例 19 青丸と赤丸に分かれる高次元 データを • Nearest Neighbor法 • 線形SVM • RBFカーネルSVM • 決定木 • ランダムフォレスト • Adaboost • Naive Bayes • 線形判別分析 • 二次判別分析 で学習し、その結果をPCAで二 次元空間上にプロットした図を 示す。色の付いたエリアがそ の予測結果で、右下の数字が Accuracy。様々な機械学習法 が開発されているが、それぞ れ得意な問題と苦手な問題が ある。
- 20. 教師あり高次元ベクトルデータの機械学習の解析例 20 青丸と赤丸に分かれる高次元 データを • Nearest Neighbor法 • 線形SVM • RBFカーネルSVM • 決定木 • ランダムフォレスト • Adaboost • Naive Bayes • 線形判別分析 • 二次判別分析 で学習し、その結果をPCAで二 次元空間上にプロットした図を 示す。色の付いたエリアがそ の予測結果で、右下の数字が Accuracy。様々な機械学習法 が開発されているが、それぞ れ得意な問題と苦手な問題が ある。
- 21.
- 22.
- 23.
- 24.
- 25. 白（活性あり）と黒（活性なし）を予測する 決定木（質問は３回まで） 25 Y > 5 Yes No X > 4 Black: 3 White: 9 START 白と予測 黒と予測 Yes No X→ Y ↓ Black: 13 White: 3 X > 5 Black: 10 White: 3 黒と予測 白と予測 Yes No Black: 2 White: 10 白と予測 黒と予測 本当は白 19 6 本当は黒 5 23 Accuracy = (19 + 23)/(19 + 6 + 5 + 23) = 0.79 Precision = 19 /(19 + 5) = 0.79 Recall = 19 / (19 + 6) = 0.76 F-measure = 0.77
- 26.