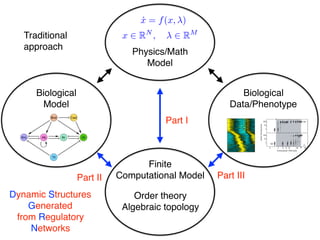
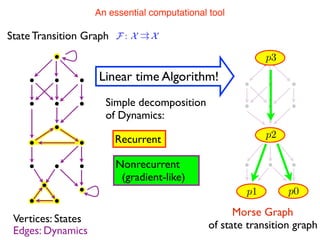
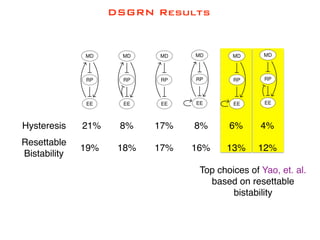
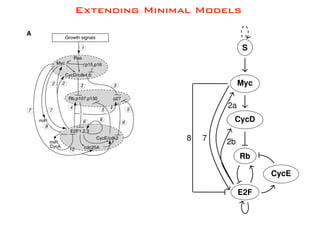
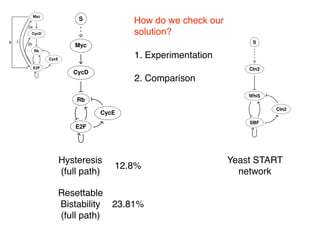
The document discusses mathematical problem-solving, attributed to Konstantin Mischaikow from Rutgers University, dated June 2018. It highlights various mathematical concepts and approaches to address complex problems. The detailed analysis and problem-solving methods are presented to aid mathematicians and researchers in their work.






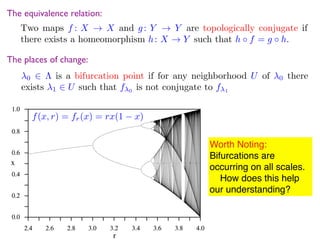



![Example
Morse tiles M(p)
Let F0
(x) = f(x).
-4 40
Atoms of lattice: G(L) = {[n, n + 1] | n = 4, . . . , 3}
Phase space: X = [ 4, 4] ⇢ R
P
1 2
3
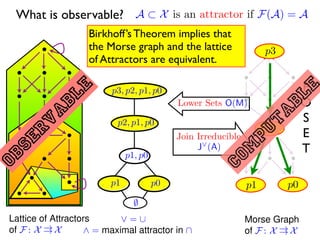
Birkhoff
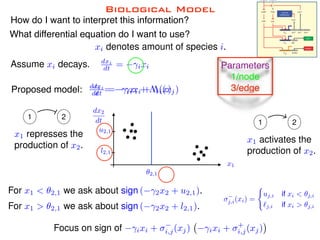
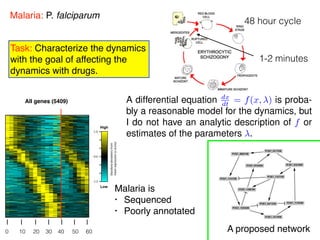
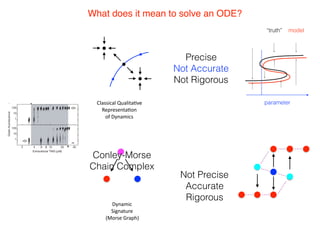
How does this relate to a differential
equation dx
dt = f(x)?
-4 40
F
F
(bistability)
A
Lattice of attracting blocks: A = {[ 3, 1], [1, 3], [ 3, 1] [ [1, 3], [ 4, 4]}
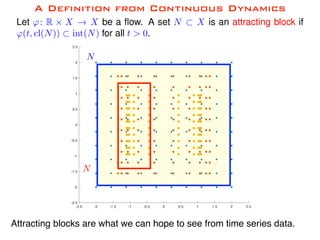
Attracting blocks are regions of phase
space that are forward invariant with
time.
F](https://image.slidesharecdn.com/klagenfurt-180625104629/85/Solving-x-20-320.jpg)