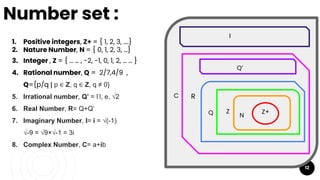
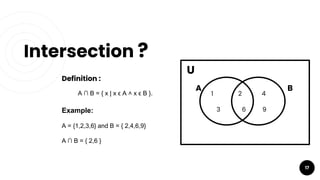
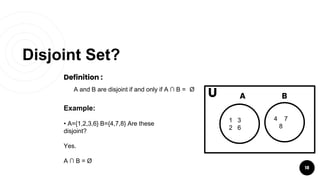
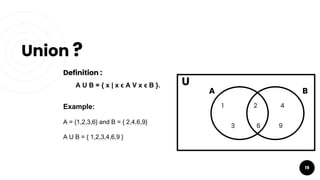
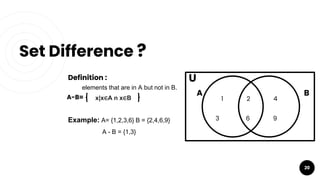
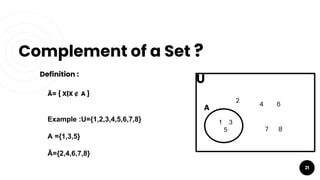
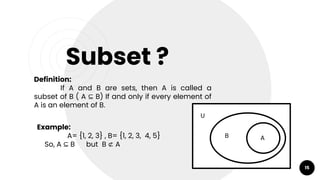
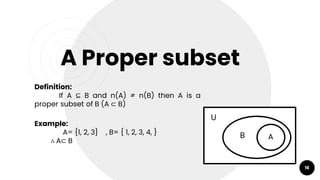
This presentation summarizes key concepts about sets, including: - Definitions of sets, order n-tuples, and the differences between them - The four types of set elements and how to represent sets - Operations on sets such as union, intersection, difference, and complement - Concepts like subsets, cardinality, and Venn diagrams - Advanced topics like power sets and Cartesian products It concludes with an example problem applying set operations and complement.

1. Presentation
on Set

2. 2
MD. SULTANUL ISLAM OVI
Lecturer
CSE at Green University of Bangladesh
Presented to:

3. 3
Presented by:
Nazmul Hasan
Id: 2139****
CSE , GUB
Arafath Islam Sezan
Id: 213****
CSE, GUB
Afrin Jahan Ananna
Id: 213******
CSE, GUB
Fahad Sarkar
Id: 213******
CSE, GUB

4. “
4
Pure mathematics is ,in its way ,the
poetry of logical ideas ……….
-Albert einstein german theoretical physicist.

5. Outline:
❏ Set.
❏ Order n-tupel.
❏ Difference
between set and
order n tuple.
❏ Set elements.
❏ Cardinality
equality.
❏ Number set.
❏ Representation
of set.
❏ Type of sets.
❏ Subset .
❏ A proper
subset.
❏ Union.
❏ Intersection.
❏ Disjoint set.
❏ Set difference.
❏ Set
complement .
❏ Venn diagram.
❏ Cartesian
product.
❏ Power set.
❏ Computer
representation.
❏ An example
question on all
operator.
5
5

6. Set ?
Example :
A={1,2,3,4,} B={Key,book,pen}
c={nazmul ,fahad,sezan,anonna}
6
Definition :
￮ ( Unordered) collection of object.

7. 7
Order n tupel?
Definition :
( Order) collection of object.
Example:
A=(1,2,3,4)

8. 8
Difference between order n-
tuple and sets:
set Order n-tuple
❏ Sets are used to represent
unordered collection.{1,4,3}
❏ Order n-tuple are used to
represent ordered collection. (1,3,4)
❏ Set use curly bracket to
represent.{}
❏ Ordre n-tuple use first bracket to
represent .()

9. 9
Set elements?
4 types :
● The number 1.
● The letter b.
● The set {x,y,z}.
● The empty set {}.
A={1,2,3,b,{x,y,z}}

10. 10
Cardinality?
Definition :
Number of elements in set .
Example :
A={1,2,3,4,5,6} n(A)=6

11. 11
Equality?
Definition :
Two sets elements are same.
.
Example:
A ={1,2,3} B={1,2,3}
A=B

12. 12
Number set :
1. Positive integers, Z+ = { 1, 2, 3, ….}
2. Nature Number, N = { 0, 1, 2, 3, …}
3. Integer , Z = { … … , -2, -1, 0, 1, 2, … … }
4. Rational number, Q = 2/7,4/9 ,
Q={p/q | p ∈ Z, q ∈ Z, q ≠ 0}
5. Irrational number, Q’ = 𐍀, e, √2
6. Real Number, R= Q+Q’
7. Imaginary Number, I= i = √(-1)
√-9 = √9×√-1 = 3i
8. Complex Number, C= a+ib
Z+
N
Z
Q
Q’
R
C
I

13. 13
Representation of
sets:
A set can be represented by :
1.listing the member of the set.
Example :
A={1,2,3,4}
Example :
{X|40<X=X<53,X is an even integers }
2.definition by property {X | X has property p}

14. 14
Type of sets :
Universal set :
Its contain every things.
A={1,2} and B={ 2,3}
U= {1, 2, 3, 4, 5, 6}
Singleton set :
Its contain only one
element.
A={123}
Finite set :
Its contains finite
number of elements.
A={1,2,3,4}
Infinite set :
Its contains infinite
number of elements.
A={1,2,3, …}
Empty set:
It contains nothing.
A={}

15. 15
Subset ?
Definition:
If A and B are sets, then A is called a
subset of B ( A ⊆ B) If and only if every element of
A is an element of B.
Example:
A= {1, 2, 3} , B= {1, 2, 3, 4, 5}
So, A ⊆ B but B ⊄ A
A
B
U

16. 16
A Proper subset
Definition:
If A ⊆ B and n(A) ≠ n(B) then A is a
proper subset of B (A ⊂ B)
Example:
A= {1, 2, 3} , B= { 1, 2, 3, 4, }
∴ A⊂ B
A
B
U

17. Intersection ?
17
Definition :
A ∩ B = { x | x ϵ A ˄ x ϵ B }.
Example:
A = {1,2,3,6} and B = { 2,4,6,9}
A ∩ B = { 2,6 }
U
A B
1 2 4
3 6 9

18. 18
Disjoint Set?
Definition :
A and B are disjoint if and only if A ∩ B = Ø
Example:
• A={1,2,3,6} B={4,7,8} Are these
disjoint?
Yes.
A ∩ B = Ø
B
1 3
2 6
4 7
8
U A B

19. Union ?
19
Definition :
A U B = { x | x ϵ A V x ϵ B }.
Example:
A = {1,2,3,6} and B = { 2,4,6,9}
A U B = { 1,2,3,4,6,9 }
U
1 2 4
3 6 9
A B

20. Set Difference ?
20
1 2 4
3 6 9
U
A B
Definition :
elements that are in A but not in B.
Example: A= {1,2,3,6} B = {2,4,6,9}
A - B = {1,3}
A-B= x|x∈A n x∈B

21. Complement of a Set ?
21
1 3
5
U
2
4 6
7 8
A
Definition :
Example :U={1,2,3,4,5,6,7,8}
A ={1,3,5}
Ã={2,4,6,7,8}
Ā= { X|X ∉ A }

22. Venn Diagram?
22
Example:
A = {a,f,s,n}
B = {a,f}
C = {i,r}
Venn diagrams are also another way
to show relationship between sets .
U
A
B
C
a f
s n
i r

23. 23
Power Set?
Definition:
Given a set S, the power set of S is the set of all subsets of
S. The power set is denoted by p(S).
❏ If S is a set with |S|= n, then |P(S)|= 2n
Example:
A={ 1, 2}
P({1, 2, 3}) = { ∅, {1}, {2}, {1, 2}}
|P(S)|= 4

24. 24
Cartesian Product?
Definition :
Given sets A and B, the cartesian product of A and B (A X B), read “A cross B”, is
the set of all ordered pairs (a,b), where a is in A and b is in B.
A x B = { (a,b) | a ϵ A ˄ b ϵ B}.
Examples : S = {1,2} and T = {a,b,c}
S x T = { (1,a), (1,b), (1,c), (2,a), (2,b), (2,c) }
T x S = { (a,1), (a, 2), (b,1), (b,2), (c,1), (c,2) }

25. 25
Computer representation of set ?
How to represent sets in the computer?
A better solution: Assign a bit in a bit string to each element in the
universal
set and set the bit to 1 if the element is present otherwise use 0
Example:
All possible elements: U={1, 2, 3, 4, 5}
Assume A={2,5}
Computer representation: A = 01001

26. 26
Example question on all operator :
U={1,2,3,4,5,6,7}
A={1,2,3,4,5,6,}
b={1,2,4,5,6,8,}
1.AUB=? →
2.A∩B=? →
3.A-B=? →
4.Ã =? →
{1,2,3,4,5,6,8}
{1,2,4,5,6}
{ 3}
{ 7}

27. 27
Any Question

28. 28
Thanks!