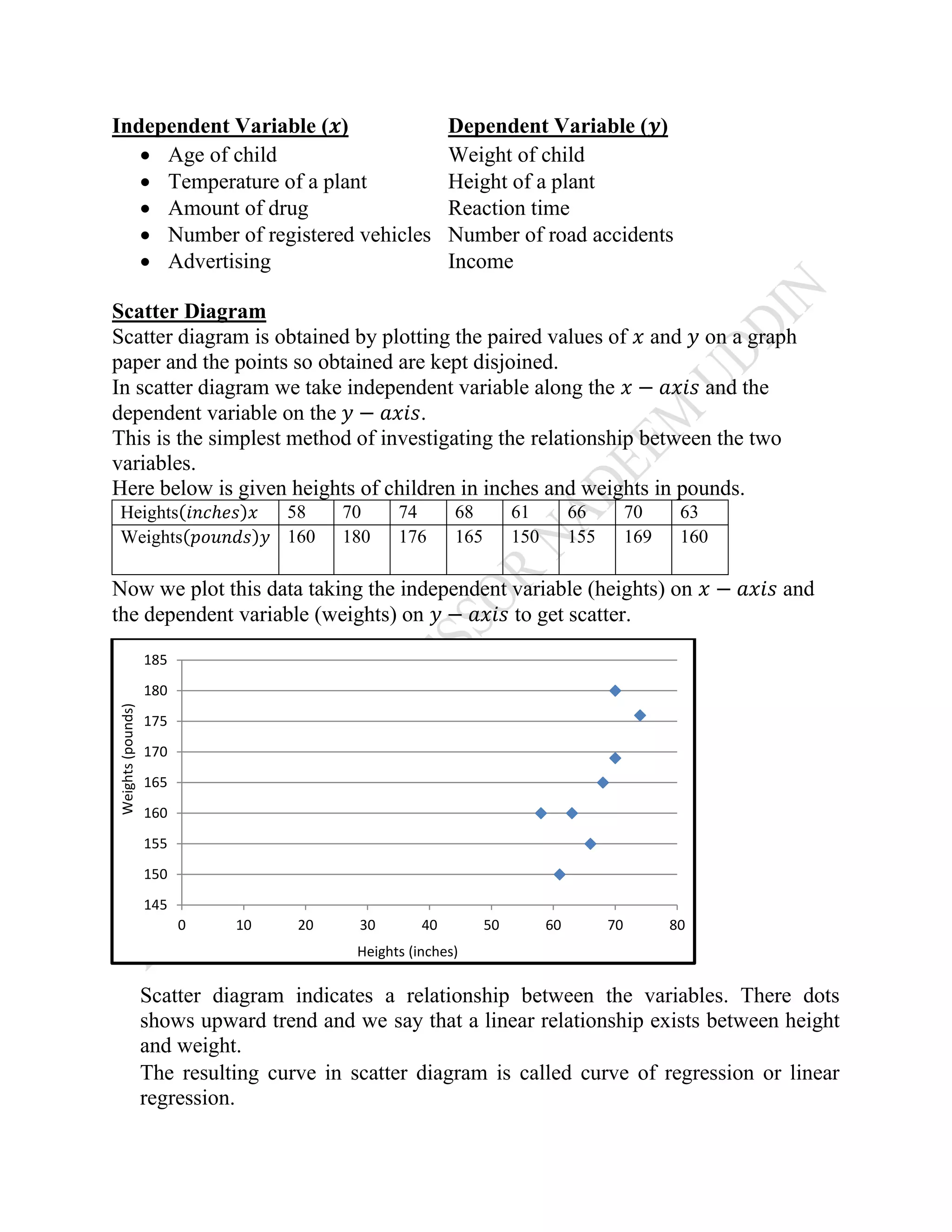
Regression is used to predict or estimate the value of a dependent variable based on the value of an independent variable. It involves plotting paired values of the independent and dependent variables on a scatter diagram to determine the relationship between them. The least squares line is an objective method for determining the line of best fit through the data points by minimizing the sum of the squares of the vertical distances of the points from the line. Examples are provided to demonstrate calculating the regression equations and using them to estimate values.

1. ROLE OF REGRESSION IN STATISTICS
BY
ASSOCIATE PROFESSOR
NADEEM UDDIN
Regression
The term regression used firstly by “Sir Frances Galton” is used for all such
problems where we have to estimate or predict one variable on the basis of another
variable.
Definition
A process by which we predict or estimate values of one dependent variable from
known values of other independent variables is called regression.
Regressand and Regressor
In regression process the dependent variable is called a random variable or
regressand and the independent variable is called fixed variable or regressor.
Dependent Variable
The variable which is to be estimated or predicted is called dependent variable.
Independent Variable
The variable on the basis of which the dependent variable is to be estimated is
called independent variable.
For Example
If we want to estimate the heights of children on the basis of their ages, then the
heights of children would be dependent variable and the ages of children would be
independent variable.
Students are some time confused with independent variable and dependent variable
here are some examples of independent and dependent variables:

2. Independent Variable (𝒙) Dependent Variable (𝒚)
• Age of child Weight of child
• Temperature of a plant Height of a plant
• Amount of drug Reaction time
• Number of registered vehicles Number of road accidents
• Advertising Income
Scatter Diagram
Scatter diagram is obtained by plotting the paired values of 𝑥 and 𝑦 on a graph
paper and the points so obtained are kept disjoined.
In scatter diagram we take independent variable along the 𝑥 − 𝑎𝑥𝑖𝑠 and the
dependent variable on the 𝑦 − 𝑎𝑥𝑖𝑠.
This is the simplest method of investigating the relationship between the two
variables.
Here below is given heights of children in inches and weights in pounds.
Heights(𝑖𝑛𝑐ℎ𝑒𝑠)𝑥 58 70 74 68 61 66 70 63
Weights(𝑝𝑜𝑢𝑛𝑑𝑠)𝑦 160 180 176 165 150 155 169 160
Now we plot this data taking the independent variable (heights) on 𝑥 − 𝑎𝑥𝑖𝑠 and
the dependent variable (weights) on 𝑦 − 𝑎𝑥𝑖𝑠 to get scatter.
Scatter diagram indicates a relationship between the variables. There dots
shows upward trend and we say that a linear relationship exists between height
and weight.
The resulting curve in scatter diagram is called curve of regression or linear
regression.
145
150
155
160
165
170
175
180
185
0 10 20 30 40 50 60 70 80
Heights (inches)
Weights(pounds)

3. The Least Square Line
After drawing scatter diagram, a free hand line can be drawn through the plotted
points, which shows trend of the variables. This free hand drawing is a “Subjective
Method” as it depends upon the personal judgment of the person drawing the line.
We need some objective method. An “Objective Method is the method of least
square”. The line obtained by this method is called “Least Square Line”.
Least Square Lines of Regression
The equation for a straight line or linear trend will be
𝑦 = 𝑎 + 𝑏𝑥
Where 𝑦 dependent variable and 𝑥 is independent variable. “𝑎” and “𝑏” are
unknown parameters determined by solving simultaneously the following normal
equation.
∑𝑦 = 𝑛𝑎 + 𝑏∑𝑥
∑𝑥𝑦 = 𝑎∑𝑥 + 𝑏∑𝑥2
The Values of “𝑎” and “𝑏” can be calculated by the following formulae which are
obtained by solving the above equations.
𝑏 =
𝑛∑𝑥𝑦 − ∑𝑥∑𝑦
𝑛∑𝑥2 − (∑𝑥)2
𝑎 =
∑𝑦
𝑛
− 𝑏 (
∑𝑥
𝑛
)
or
𝑎 = 𝑦̅ − 𝑏𝑥̅
If the variable “𝑥” is taken as dependent variable and “𝑦” is taken as independent
variable then the least square line is
𝑥 = 𝑐 + 𝑑𝑦
The normal equations are
∑𝑥 = 𝑛𝑐 + 𝑑∑𝑦
∑𝑥𝑦 = 𝑐∑𝑦 + 𝑑∑𝑦2
By solving the above equations, the value of “𝑐” and “𝑑” can be calculated as
𝑑 =
𝑛∑𝑥𝑦 − ∑𝑥∑𝑦
𝑛∑𝑦2 − (∑𝑦)2
𝑐 =
∑𝑥
𝑛
− 𝑑(
∑𝑦
𝑛
)
Or
𝑐 = 𝑥̅ − 𝑑𝑦̅

4. Example-1:
Determine
(i) the regression equation of 𝑦 on 𝑥, and estimate 𝑦 at 𝑥 = 2.
(ii) the regression equation of 𝑥 on 𝑦, and estimate 𝑥 at y = 4.
𝒙 1 3 3 4 5 5
𝒚 5 3 2 2 0 1
Solution:
𝒙 𝒚 𝒙𝒚 𝒙 𝟐
𝒚 𝟐
1 5 5 1 25
3 3 9 9 9
3 2 6 9 4
4 2 8 16 4
5 0 0 25 0
5 1 5 25 1
∑x=21 ∑y=13 ∑xy=33 ∑x2
=85 ∑y2
=43
Regression equation 𝑦 on 𝑥.
y a bx= +
𝑏 =
𝑛∑𝑥𝑦−∑𝑥∑𝑦
𝑛∑𝑥2−(∑𝑥)2
𝑏 =
6(33)−(21)(13)
6(85)−(21)2
𝑏 =
198−273
510−441
𝑏 = −
75
69
𝒃 = −𝟏. 𝟎𝟗

5. 𝑎 =
∑𝑦
𝑛
− 𝑏 (
∑𝑥
𝑛
)
𝑎 =
13
6
− (−1.09)(
21
6
)
𝑎 = 2.17 + 3.815
𝑎 = 5.98
Line of Regression
𝑦 = 𝑎 + 𝑏𝑥
𝑦 = 5.98 + (−1.09)𝑥
𝒚 = 𝟓. 𝟗𝟖 − 𝟏. 𝟎𝟗𝒙
When 𝑥 = 2
𝑦̂ = 5.98 − 1.09(2)
𝑦̂ = 5.98 − 2.18
𝒚̂ = 𝟑. 𝟖
(ii) Regression equation 𝑥 on 𝑦
𝑥 = 𝑐 + 𝑑𝑦
𝑑 =
𝑛∑𝑥𝑦−∑𝑥∑𝑦
𝑛∑𝑦2−(∑𝑦)2
𝑑 =
(6)(33)−(21)(13)
(6)(43)−(13)2
𝑑 =
198−273
258−169
𝑑 = −
75
89

6. 𝒅 = −𝟎. 𝟖𝟒
𝑐 =
∑𝑥
𝑛
− 𝑑(
∑𝑦
𝑛
)
𝑐 =
21
6
− (−0.84)(
13
6
)
𝑐 = 3.5 + 0.84(2.17)
𝑐 = 3.5 + 1.82
𝒄 = 𝟓. 𝟑𝟐
𝑥 = 𝑐 + 𝑑𝑦
𝑥 = 5.32 + (−0.84)𝑦
𝒙 = 𝟓. 𝟑𝟐 − 𝟎. 𝟖𝟒𝒚
When 𝑦 = 4
𝑥̂ = 5.32 − 0.84(4)
𝑥̂ = 5.32 − 3.36
𝒙̂ = 𝟏. 𝟗𝟔

7. Example-2:
The heights and weights of six men are given below.
Height(𝑚𝑒𝑡𝑒𝑟𝑠) 2.00 1.80 1.85 1.72 1.75 1.79
Weight(𝑘𝑔𝑠) 85.0 78.0 80.0 74.0 75.0 76.0
i) Determine both the lines of regression.
ii) Estimate weight when height is1.70 𝑚𝑒𝑡𝑒𝑟𝑠.
iii) Estimate height when weight is70.0 𝑘𝑔.
Solution:
Height
(𝒎𝒆𝒕𝒆𝒓𝒔) 𝒙
Weight (𝒌𝒈𝒔)
𝒚
𝒙𝒚 𝒙 𝟐
𝒚 𝟐
2.00 85.0 170.00 4.0000 7225
1.80 78.0 140.40 3.2400 6084
1.85 80.0 148.00 3.4225 6400
1.72 74.0 127.28 2.9584 5476
1.75 75.0 131.25 3.0625 5625
1.79 76.0 136.04 3.2041 5776
∑x=10.91 ∑y=468 ∑xy=852.97 ∑x2
=19.8875 ∑y2
=36586
i) Regression line 𝑦 on 𝑥
𝑦 = 𝑎 + 𝑏𝑥
𝑏 =
𝑛∑𝑥𝑦−∑𝑥∑𝑦
𝑛∑𝑥2−(∑𝑥)2
𝑏 =
6(852.97)−(10.91)(468)
6(19.8875)−(10.91)2
𝑏 =
5117.82−5105.88
119.325−119.0281
𝑏 =
11.94
0.2969
𝒃 = 𝟒𝟎. 𝟐𝟐
𝑎 =
∑𝑦
𝑛
− 𝑏(
∑𝑥
𝑛
)

8. 𝑎 =
468
6
− (40.22) (
10.91
6
)
𝑎 = 78 − (40.22)(1.82)
𝑎 = 78 − 73.20
𝒂 = 𝟒. 𝟖
𝑦 = 𝑎 + 𝑏𝑥
𝑦 = 4.8 + 40.22𝑥
Regression line 𝑥 on 𝑦
𝑥 = 𝑐 + 𝑑𝑦
𝑑 =
𝑛∑𝑥𝑦−∑𝑥∑𝑦
𝑛∑𝑦2−(∑𝑦)2
𝑑 =
6(852.97)−(10.9)(468)
6(36586)−(468)2
𝑑 =
11.94
492
𝒅 = 𝟎. 𝟎𝟐𝟒
𝑐 =
∑𝑥
𝑛
− 𝑑 (
∑𝑦
𝑛
)
𝑐 =
10.91
6
− (0.024) (
468
6
)
𝑐 = 1.82 − (0.024)(78)
𝑐 = 1.82 − 1.872
𝒄 = −𝟎. 𝟎𝟓𝟐

9. 𝑥 = 𝑐 + 𝑑𝑦
𝒙 = −𝟎. 𝟎𝟓𝟐 + 𝟎. 𝟎𝟐𝟒𝒚
ii) Estimate weight when height is 𝑥 = 1.70 meters
𝑦̂ = 4.8 + 40.22(1.70)
𝑦̂ = 4.8 + 68.374
𝒚̂ = 𝟕𝟑 𝒌𝒈
The estimated value of weight is 73𝑘𝑔 when height is1.7 𝑚𝑒𝑡𝑒𝑟𝑠.
Now estimate height when weight is 𝑦 = 70.0 𝑘𝑔
𝑥̂ = −0.052 + 0.024(7.00)
𝑥̂ = −0.052 + 1.68
𝒙̂ = 𝟏. 𝟔𝟑 𝒎𝒆𝒕𝒆𝒓𝒔
The estimated value of height is 1.63 𝑚𝑒𝑡𝑒𝑟𝑠 when weight is70 𝑘𝑔.