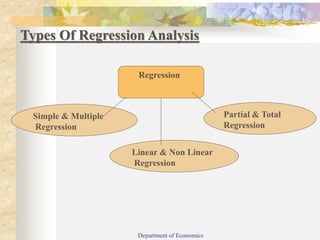
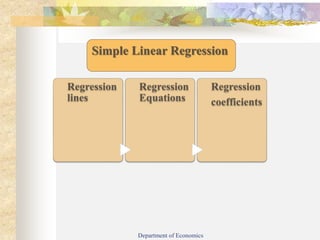
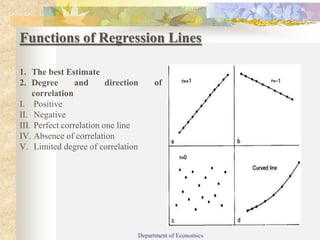
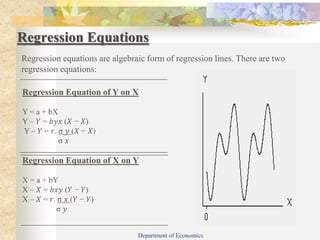
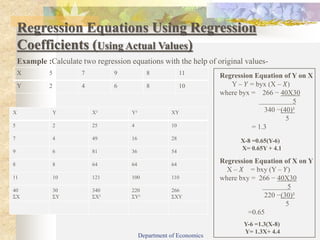
This document provides an introduction to basic statistics and regression analysis. It defines regression as relating to or predicting one variable based on another. Regression analysis is useful for economics and business. The document outlines the objectives of understanding simple linear regression, regression coefficients, and merits and demerits of regression analysis. It describes types of regression including simple and multiple regression. Key concepts explained in more detail include regression lines, regression equations, regression coefficients, and the difference between correlation and regression. Examples are provided to demonstrate calculating regression equations using different methods.