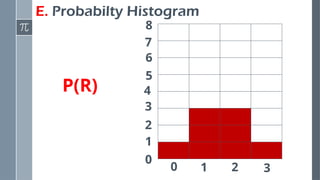
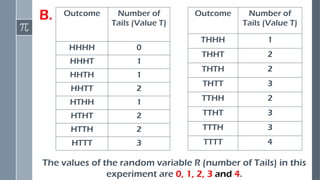
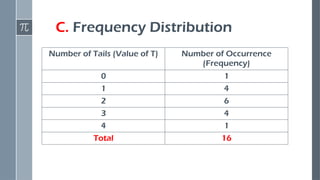
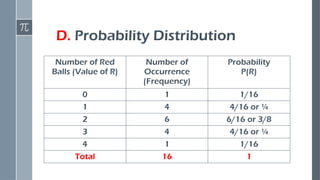
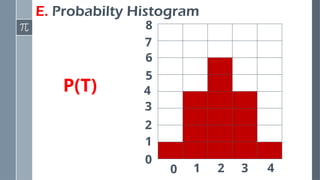
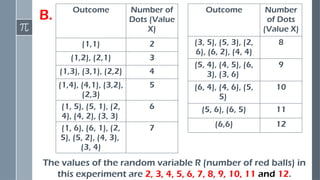
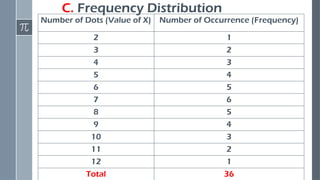
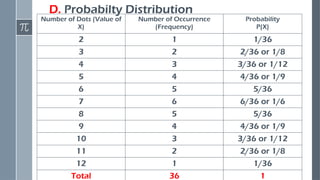
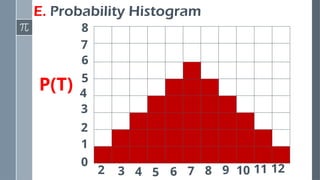
Here’s a clear and classroom-friendly PowerPoint description you can place in your introduction slide or overview slide: Random Variables – Presentation Description This presentation introduces the concept of random variables, a fundamental idea in probability and statistics. It explains how random variables are used to assign numerical values to the outcomes of a random experiment. The discussion covers the two main types of random variables—discrete and continuous—along with their characteristics, examples, and real-life applications. 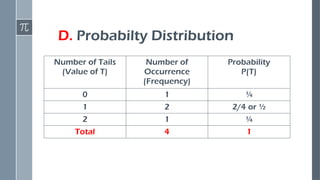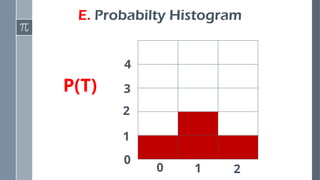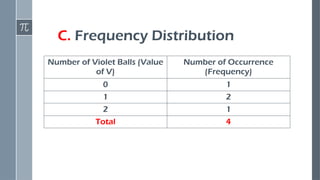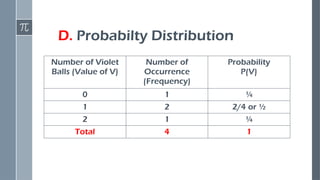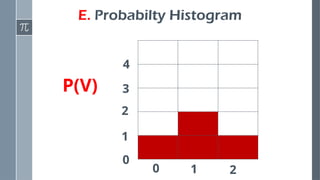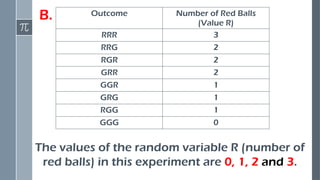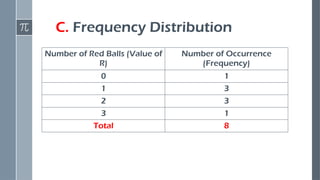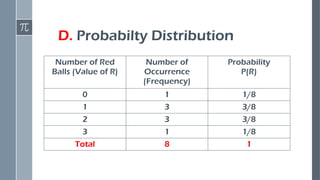Students will learn how to: Identify random variables in different situations Distinguish between discrete and continuous random variables Construct probability distributions Compute the mean (expected value) of a discrete random variable By the end of this lesson, learners will understand how random variables help us measure uncertainty and make informed decisions using probability. If you want, I can also create: A shorter version (for title slide only) A more detailed academic version Or a student-friendly version written in simpler language 😊

1. Quarter 3 – Module 1
Random Variables and
Probability Distribution

2. 1. Any activity which can be
done repeatedly under
similar conditions.
EXPERIMENT OR TRIAL

3. 2. The set of all possible
outcomes in an experiment.
SAMPLE SPACE

4. 3. A subset of a sample
space.
EVENT

5. 4. The elements in a sample
space.
OUTCOME

6. 5. The ratio of the number of
favorable outcomes to the
number of possible outcome
s
PROBABILITY

7. 6. In how many way/s can a
coin fall?
Ans: 2
H T

8. 7. In how many ways can
two coins fall?
Ans: 4 H H
H T
H
T
T T

9. 8. If three coins are tossed,
in how many ways can they
fall?
Ans: 8
H H
H T
H
T
T
H
T
H
H H
T T T
T H H
T T
H
T T H

10. 9. In how many ways can a
die fall?
Ans: 6
1 2 3 4 5 6

11. 10. In how many ways can
two dice fall?
Ans: 36

12. 11. In how many ways are
there in tossing a coin and
rolling a die?
Ans: 12
H 1
H
H
H
2
3
4
H 5
H 6
T 1
2
T
3
T
4
T
5
T
6
T

13. 12. Mary Ann, Hazel, and
Analyn want to know what
numbers can be assigned
for
the frequency of heads that
will occur in tossing three
coins. Can you help
Ans: 0, 1, 2, 3

14. Random Variables
Random Variables
A random variable is a result of
chance event, that you can
measure or count.

15. Random Variables
Random Variables
A random variable is a result of chance
event, that you can measure or count.
A random variable is a numerical quantity
that is assigned to the outcome of an
experiment.

16. Random Variables
A random variable is a result of chance event, that
you can measure or count.
A random variable is a numerical quantity that is
assigned to the outcome of an experiment.
A random variable is a quantitative variable
which values depends on change..
NOTE: We use capital letters to represent a random variable.

17. Example:
1. Suppose two coins are tossed and we are
interested to determine the number of tails
that will come out.
Let us use T to represent the number of tails
that will come out.
Determine the values of the random variable T.

18. A. Sample space: S = {HH, HT, TH, TT}
Outcome Number of Tails (Value T)
HH 0
HT 1
TH 1
TT 2
The values of the random variable T
(number of tails) in this experiment
are 0, 1 and 2.
B.

19. C. Frequency Distribution
Number of Tails (Value of T) Number of Occurrence
(Frequency)
0 1
1 2
2 1
Total 4

20. D. Probabilty Distribution
Number of Tails
(Value of T)
Number of
Occurrence
(Frequency)
Probability
P(T)
0 1 ¼
1 2 2/4 or ½
2 1 ¼
Total 4 1

21. E. Probabilty Histogram
3
2
1
0
0 1 2
P(T)
4

22. Example:
2. Two balls are drawn in succession without
replacement from an urn containing 5 orange
balls and 6 violet balls.
Let V be the random variable representing the
number of violet balls.
Find the values of the random variable V.

23. Example:
3. Two balls are drawn in succession without replacement
from an urn containing 5 orange balls and 6 violet balls.
Let V be the random variable representing the number of
violet balls.

24. Random Variables
Example:
Two balls are drawn in succession without replacement from an urn containing
5 orange balls and 6 violet balls.
Let V be the random variable representing the number of violet balls.

25. Random Variables
Example:
Two balls are drawn in succession without replacement from an urn containing
5 orange balls and 6 violet balls.
Let V be the random variable representing the number of violet balls.

26. Random Variables
Example:
Two balls are drawn in succession without replacement from an urn containing
5 orange balls and 6 violet balls.
Let V be the random variable representing the number of violet balls.

27. Random Variables
Example:
Two balls are drawn in succession without replacement from an urn containing
5 orange balls and 6 violet balls.
Let V be the random variable representing the number of violet balls.

28. Random Variables
Example:
Two balls are drawn in succession without replacement from an urn containing
5 orange balls and 6 violet balls.
Let V be the random variable representing the number of violet balls.

29. Random Variables
Example:
Two balls are drawn in succession without replacement from an urn containing
5 orange balls and 6 violet balls.
Let V be the random variable representing the number of violet balls.

30. Random Variables
Example:
Two balls are drawn in succession without replacement from an urn containing
5 orange balls and 6 violet balls.
Let V be the random variable representing the number of violet balls.

31. A. Sample space: S = {OO, OV, VO, VV}
Outcome Number of Violet balls
OO 0
OV 1
VO 1
VV 2
The values of the random variable V
(number of violet balls) in this
experiment are 0, 1 and 2.
B.

32. C. Frequency Distribution
Number of Violet Balls (Value
of V)
Number of Occurrence
(Frequency)
0 1
1 2
2 1
Total 4

33. D. Probabilty Distribution
Number of Violet
Balls (Value of V)
Number of
Occurrence
(Frequency)
Probability
P(V)
0 1 ¼
1 2 2/4 or ½
2 1 ¼
Total 4 1

34. E. Probabilty Histogram
3
2
1
0
0 1 2
P(V)
4

35. Example:
4. A basket contains 10 red balls and 4 green
balls. If three balls are taken from the basket
one after the other, determine the possible
values of the random variable R representing
the number of red balls.

36. Random Variables
Example:
A basket contains 10 red balls and 4 green balls. If three balls are taken
from the basket one after the other, determine the possible values of the
random variable R representing the number of red balls.

37. Random Variables
Example:
A basket contains 10 red balls and 4 green balls. If three balls are taken
from the basket one after the other, determine the possible values of the
random variable R representing the number of red balls.

38. Random Variables
Example:
A basket contains 10 red balls and 4 green balls. If three balls are taken
from the basket one after the other, determine the possible values of the
random variable R representing the number of red balls.

39. Random Variables
Example:
A basket contains 10 red balls and 4 green balls. If three balls are taken
from the basket one after the other, determine the possible values of the
random variable R representing the number of red balls.

40. Random Variables
Example:
A basket contains 10 red balls and 4 green balls. If three balls are taken
from the basket one after the other, determine the possible values of the
random variable R representing the number of red balls.

41. Random Variables
Example:
A basket contains 10 red balls and 4 green balls. If three balls are taken
from the basket one after the other, determine the possible values of the
random variable R representing the number of red balls.

42. Random Variables
Example:
A basket contains 10 red balls and 4 green balls. If three balls are taken
from the basket one after the other, determine the possible values of the
random variable R representing the number of red balls.

43. Random Variables
Example:
A basket contains 10 red balls and 4 green balls. If three balls are taken
from the basket one after the other, determine the possible values of the
random variable R representing the number of red balls.

44. Random Variables
Example:
A basket contains 10 red balls and 4 green balls. If three balls are taken
from the basket one after the other, determine the possible values of the
random variable R representing the number of red balls.

45. Random Variables
Example:
A basket contains 10 red balls and 4 green balls. If three balls are taken
from the basket one after the other, determine the possible values of the
random variable R representing the number of red balls.

46. Random Variables
Example:
A basket contains 10 red balls and 4 green balls. If three balls are taken
from the basket one after the other, determine the possible values of the
random variable R representing the number of red balls.

47. A. Sample space:
S = {RRR, RRG, GWG, GRR,
GGR, GRG, RGG, GGG}

48. Outcome Number of Red Balls
(Value R)
RRR 3
RRG 2
RGR 2
GRR 2
GGR 1
GRG 1
RGG 1
GGG 0
The values of the random variable R (number of
red balls) in this experiment are 0, 1, 2 and 3.
B.

49. C. Frequency Distribution
Number of Red Balls (Value of
R)
Number of Occurrence
(Frequency)
0 1
1 3
2 3
3 1
Total 8

50. D. Probabilty Distribution
Number of Red
Balls (Value of R)
Number of
Occurrence
(Frequency)
Probability
P(R)
0 1 1/8
1 3 3/8
2 3 3/8
3 1 1/8
Total 8 1

51. E. Probabilty Histogram
3
2
1
0
0 1 2
P(R) 4
5
6
7
8
3

52. Examples:
4. Four coins are tossed. Let T
be the random variable
representing the number of
tails that occur. Find the values
of the random variable T.

53. A. Sample space:
S = {HHHH, HHHT, HHTH, HHTT,
HTHH, HTHT, HTTH, HTTT, THHH,
THHT, THTH, THTT, TTHH, TTHT,
TTTH, TTTT}

54. Outcome Number of
Tails (Value T)
HHHH 0
HHHT 1
HHTH 1
HHTT 2
HTHH 1
HTHT 2
HTTH 2
HTTT 3
The values of the random variable R (number of Tails) in this
experiment are 0, 1, 2, 3 and 4.
B. Outcome Number of
Tails (Value T)
THHH 1
THHT 2
THTH 2
THTT 3
TTHH 2
TTHT 3
TTTH 3
TTTT 4

55. C. Frequency Distribution
Number of Tails (Value of T) Number of Occurrence
(Frequency)
0 1
1 4
2 6
3 4
4 1
Total 16

56. D. Probability Distribution
Number of Red
Balls (Value of R)
Number of
Occurrence
(Frequency)
Probability
P(R)
0 1 1/16
1 4 4/16 or ¼
2 6 6/16 or 3/8
3 4 4/16 or ¼
4 1 1/16
Total 16 1

57. E. Probabilty Histogram
3
2
1
0
0 1 2
P(T) 4
5
6
7
8
3 4

58. Examples:
5. A pair of dice is rolled. Let X be
the random variable representing
the sum of the number of dots on
the top faces. Find the values of the
random variable X.

59. A. Sample space:
S = {(1,1), (1,2), (1,3), (1,4), (1,5),
(1,6), (2,1), (2,2), (2,3), (2,4), (2,5),
(2,6), (3, 1), (3, 2), (3, 3), (3, 4),
(3,5), (3,6), (4,1), (4,2), (4,3), (4,4),
(4,5), (4,6), (5,1), (5,2), (5,3), (5,4),
(5,5), (5,6), (6,1), (6,2), (6,3), (6,4),
(6,5), (6,6)}

60. Outcome Number of
Dots (Value
X)
(1,1) 2
(1,2), (2,1) 3
(1,3), (3,1), (2,2) 4
(1,4), (4,1), (3,2),
(2,3)
5
(1, 5), (5, 1), (2,
4), (4, 2), (3, 3)
6
(1, 6), (6, 1), (2,
5), (5, 2), (4, 3),
(3, 4)
7
The values of the random variable R (number of red balls) in
this experiment are 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12.
B. Outcome Number
of Dots
(Value X)
(3, 5), (5, 3), (2,
6), (6, 2), (4, 4)
8
(5, 4), (4, 5), (6,
3), (3, 6)
9
(6, 4), (4, 6), (5,
5)
10
(5, 6), (6, 5) 11
(6,6) 12

61. C. Frequency Distribution
Number of Dots (Value of X) Number of Occurrence (Frequency)
2 1
3 2
4 3
5 4
6 5
7 6
8 5
9 4
10 3
11 2
12 1
Total 36

62. D. Probabilty Distribution
Number of Dots (Value of
X)
Number of Occurrence
(Frequency)
Probability
P(X)
2 1 1/36
3 2 2/36 or 1/8
4 3 3/36 or 1/12
5 4 4/36 or 1/9
6 5 5/36
7 6 6/36 or 1/6
8 5 5/36
9 4 4/36 or 1/9
10 3 3/36 or 1/12
11 2 2/36 or 1/8
12 1 1/36
Total 36 1

63. E. Probability Histogram
3
2
1
0
2 3 4
P(T) 4
5
6
7
8
5 6 7 8 9 10 11 12

64. Discrete and Continuous
Random Variable
A discrete random variable
has a countable number of
possible values.

65. Discrete and Continuous
Random Variable
A discrete random variable has a countable
number of possible values.
A continuous random
Variable can assume an infinite
number of values in one or more
intervals.

66. Discrete Random Variable
o Number of pens in a box
o Number of ants in colony
o Number of ripe bananas in a basket
o Number of COVID 19 positive cases in
SJDM, Bulacan
o Number of defective batteries

67. Continuous Random Variable
o Amount of antibiotics in a vial
o Length of electric wires
o Voltage of car batteries
o Weight of newborn in the hospital
o Amount of sugar in a cup of coffee