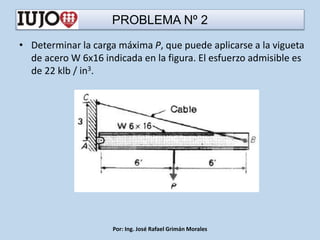
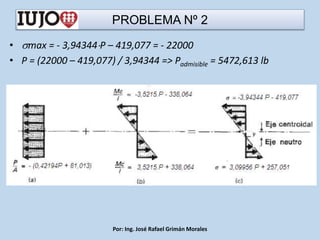
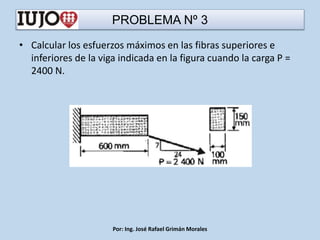
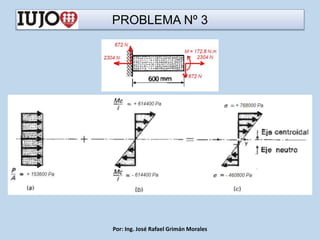
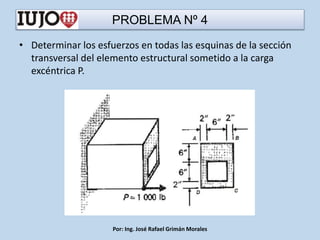
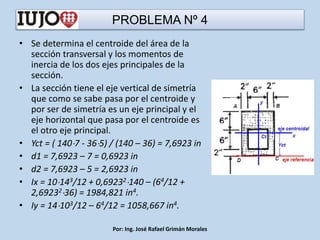
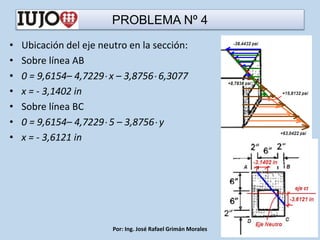
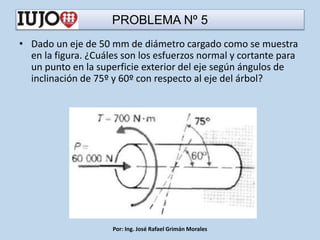
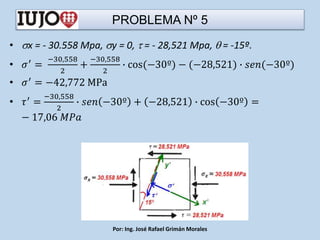
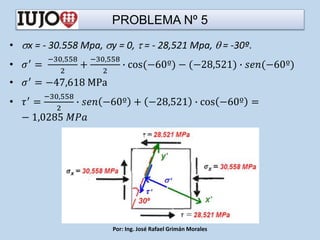
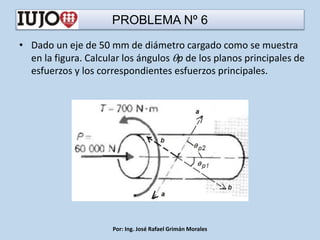
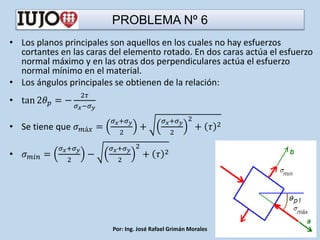
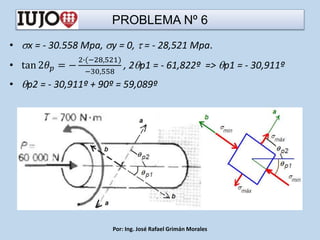
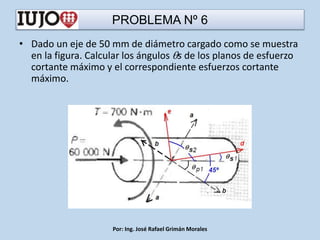
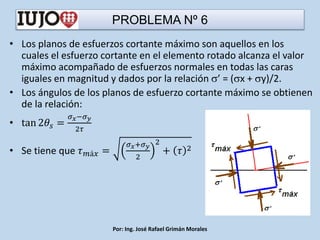
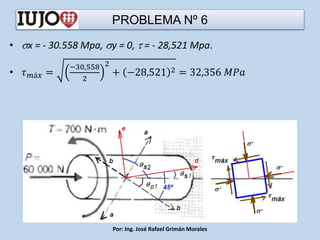
The document presents various engineering problems involving calculations of stress and forces in structural elements due to applied loads. Specific cases include determining normal and shear stresses in beams and axes, while applying principles of equilibrium and superposition to find maximum and minimum stresses at critical points. Throughout, it utilizes formulas for bending moments, cross-sectional areas, and moments of inertia to solve these problems.