JB
Uploaded byJoão Baltazar
PDF, PPTX62 views

Prediction of the Open-Water Performance of Ducted Propellers With a Panel Method

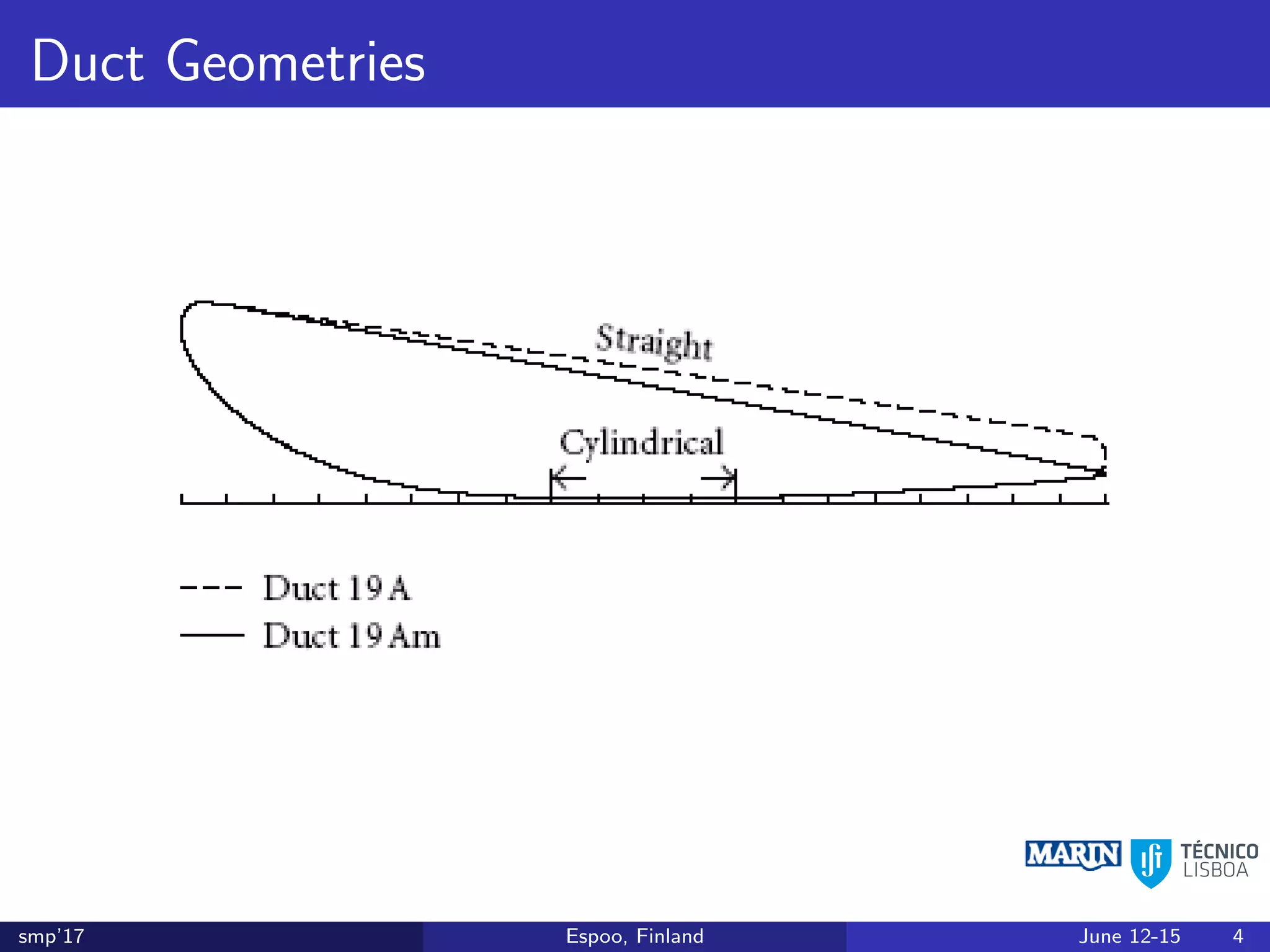
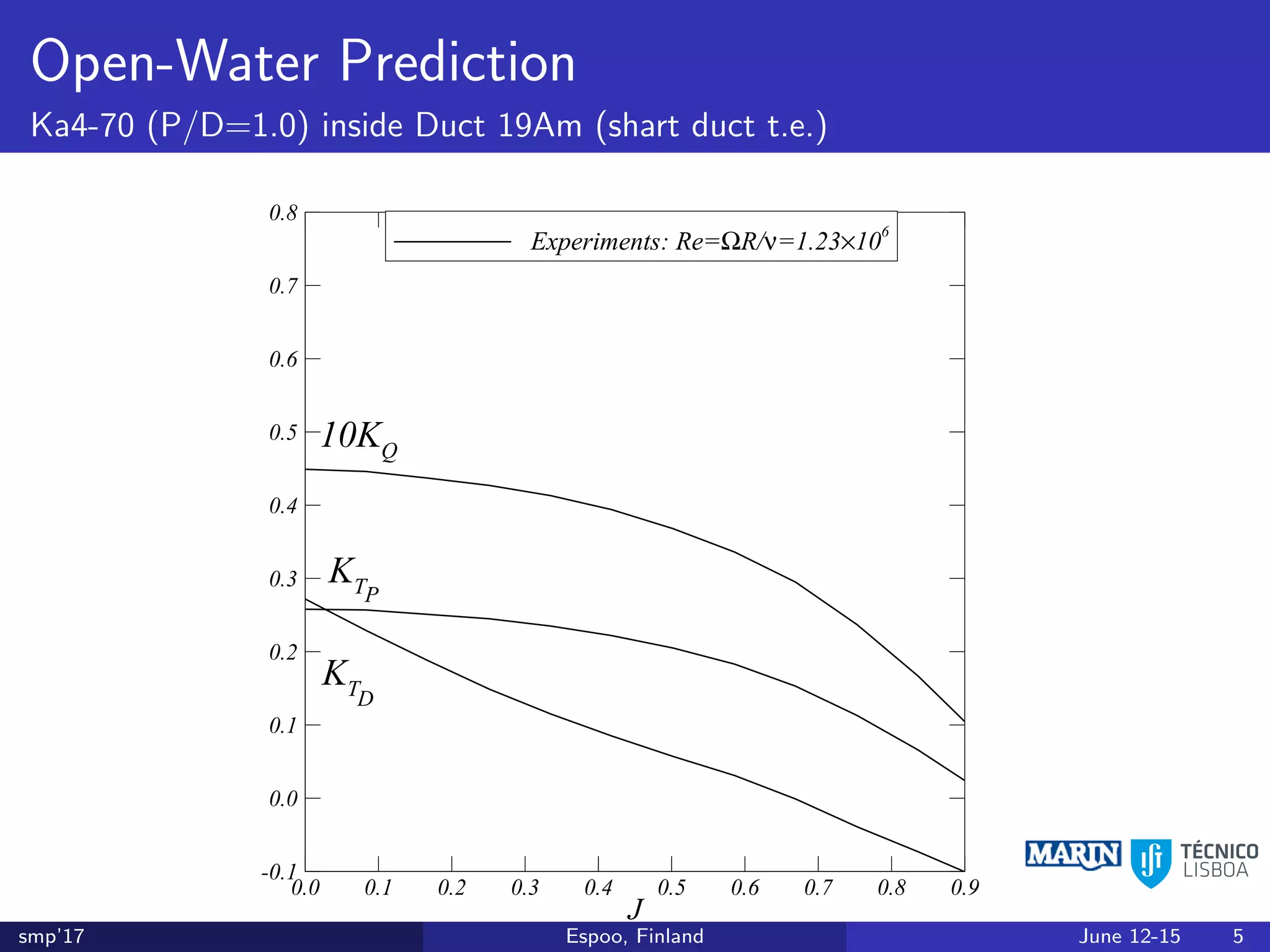
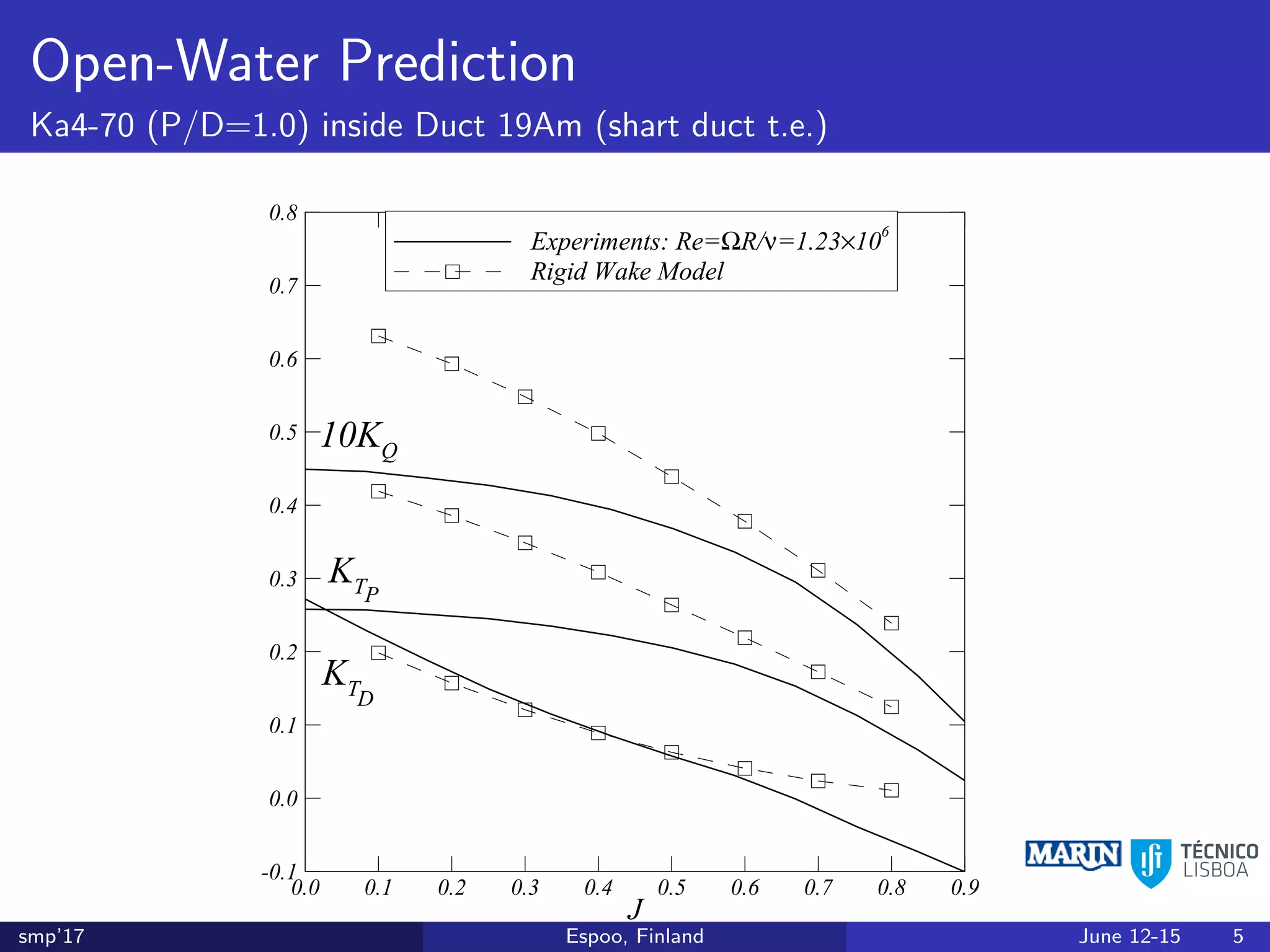
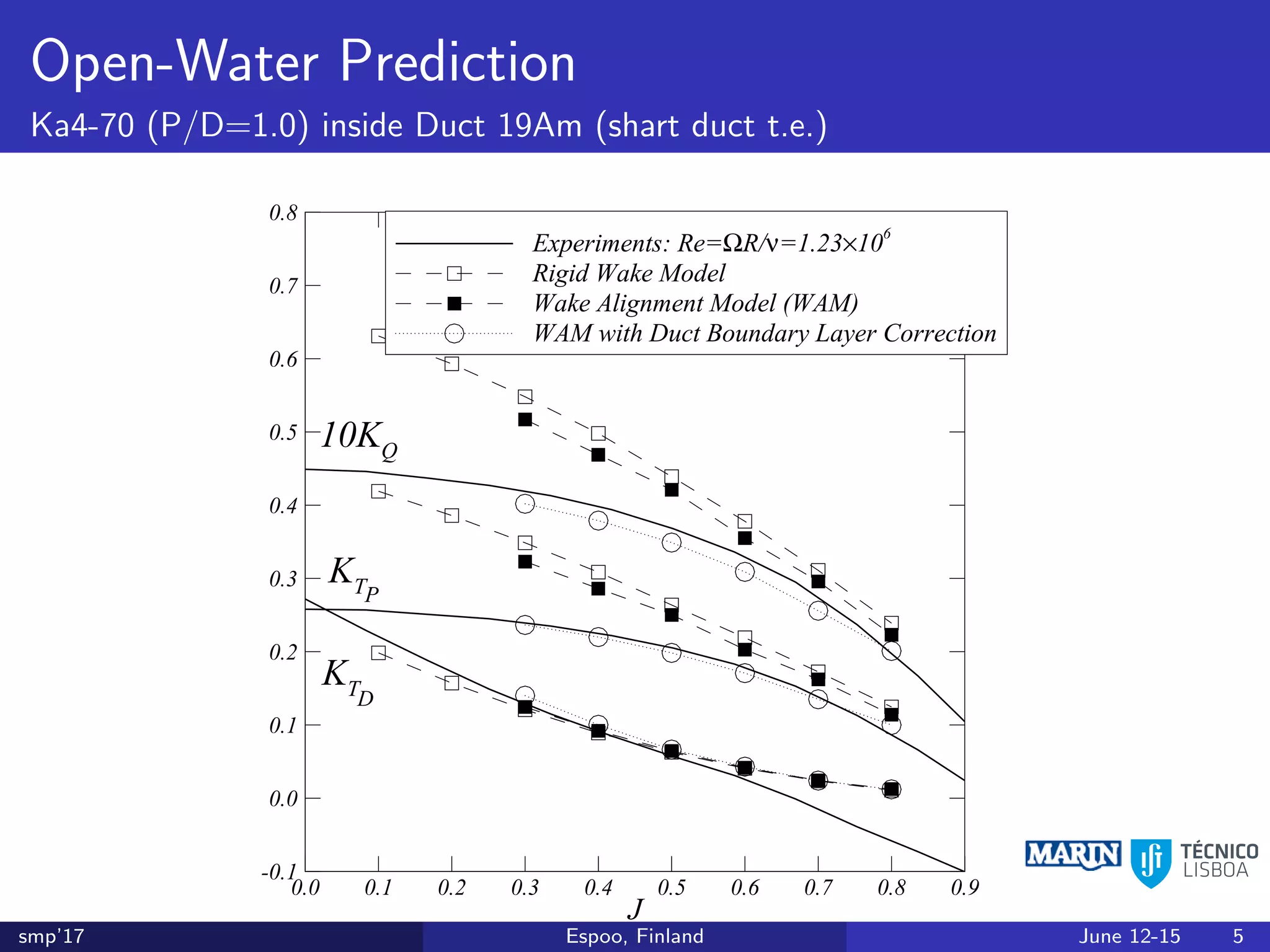
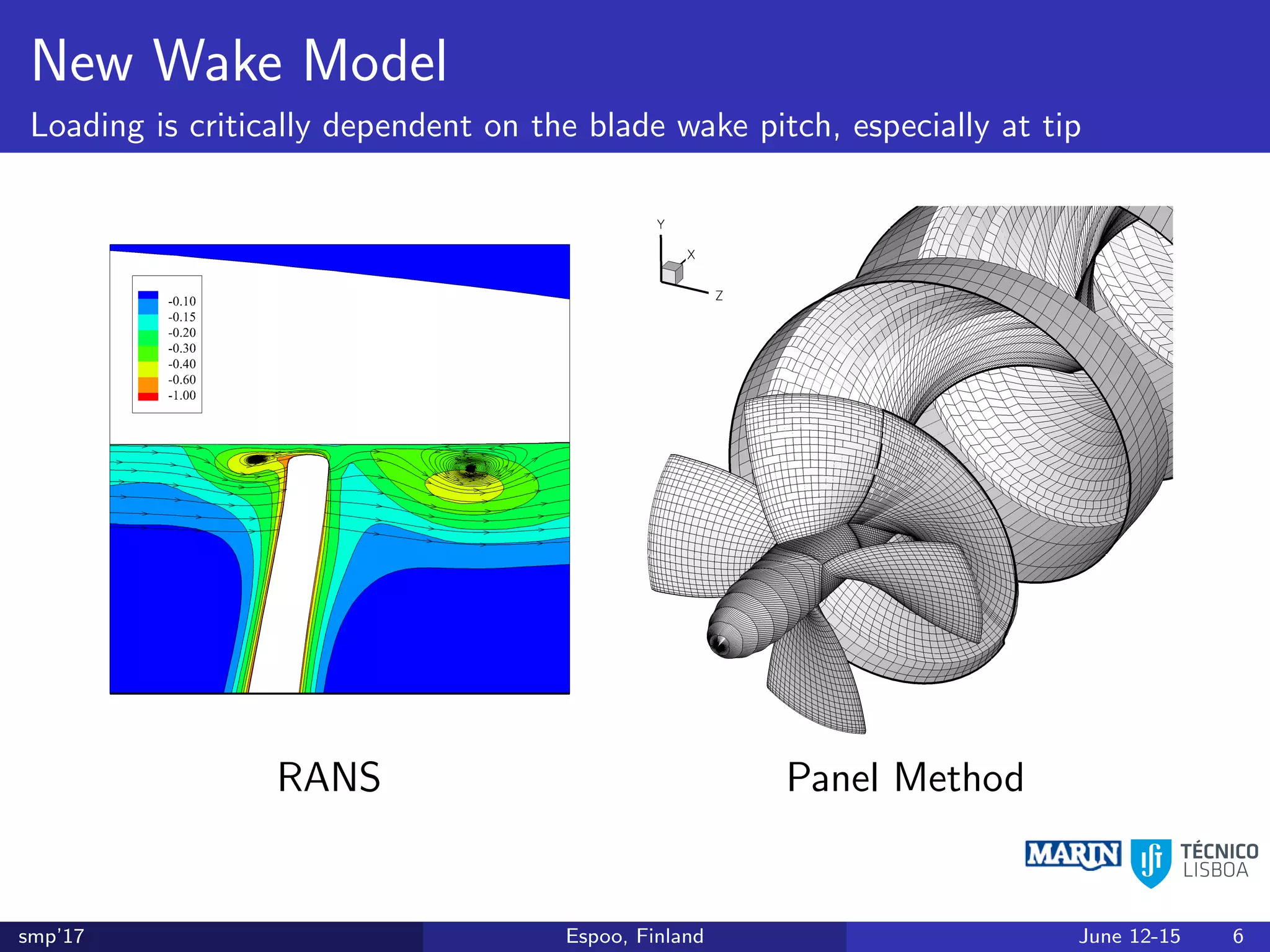
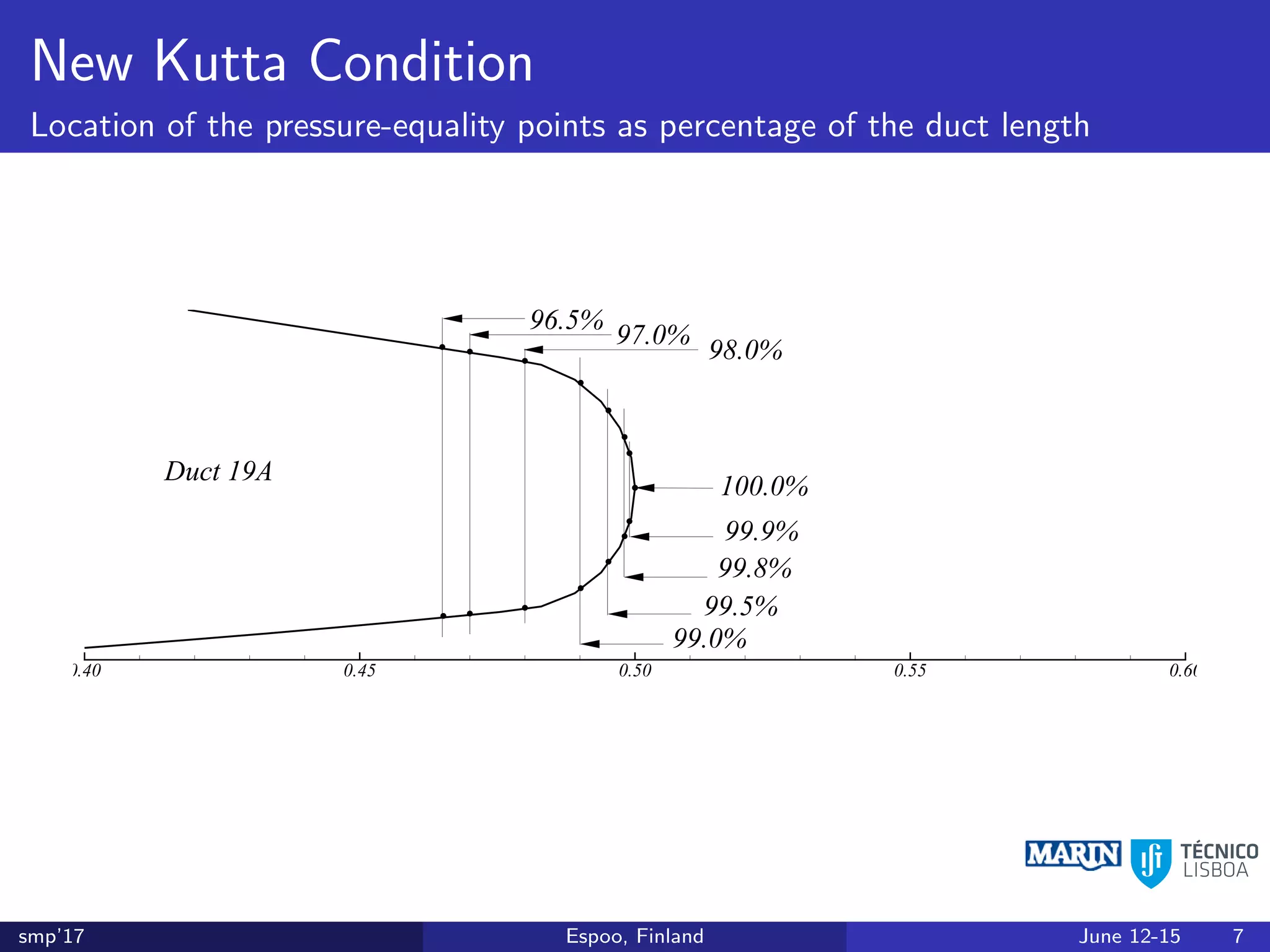
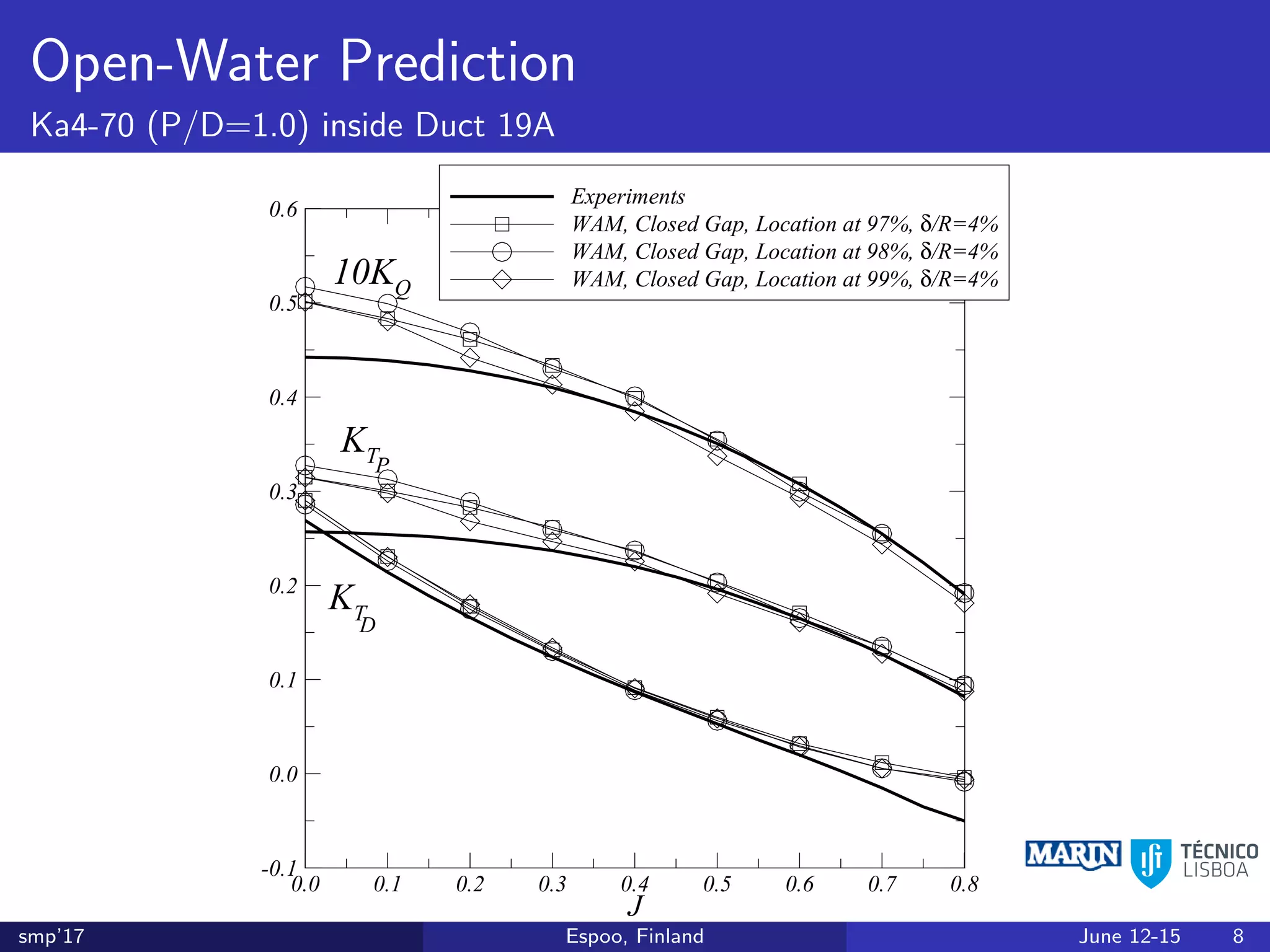
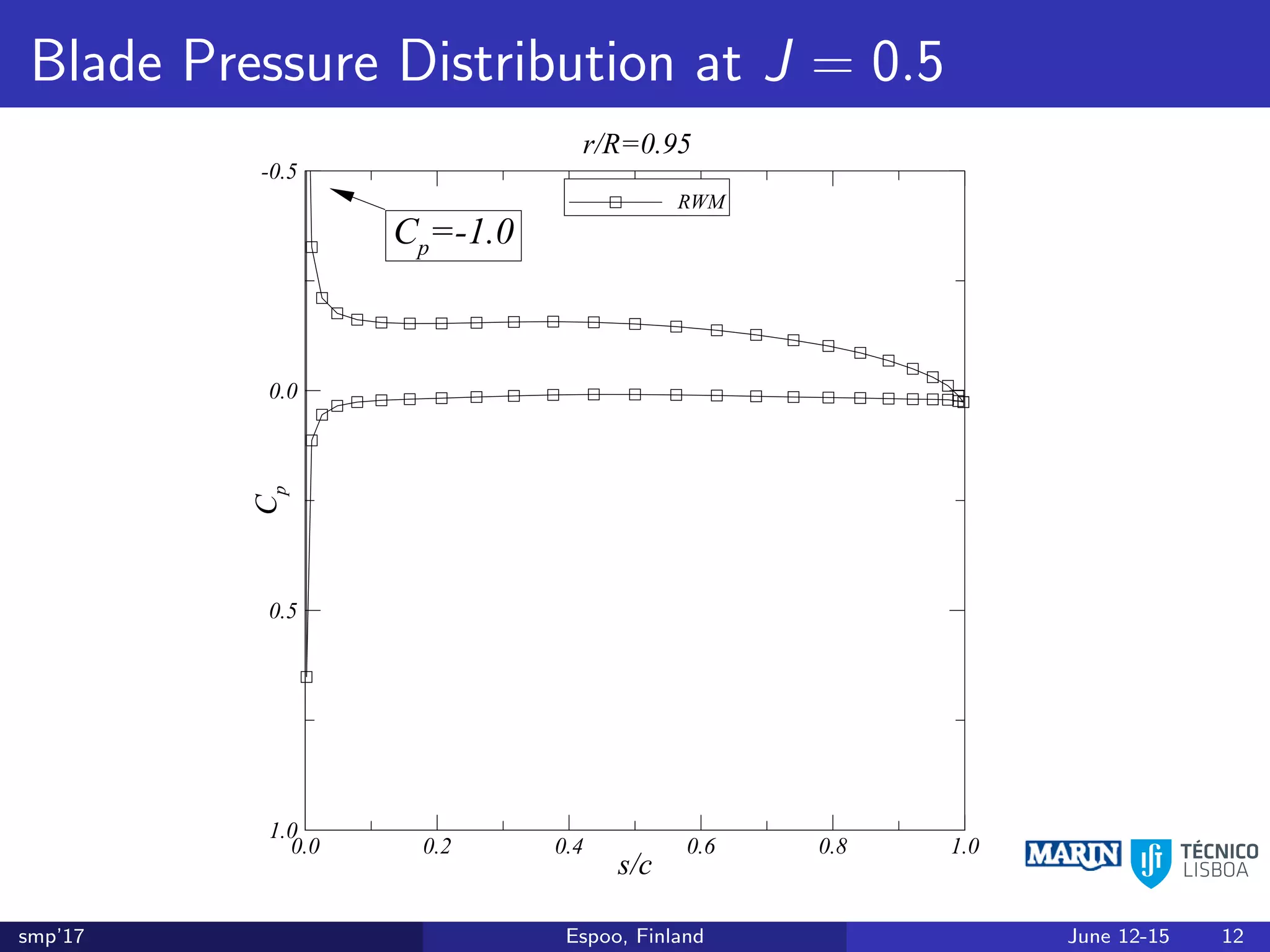
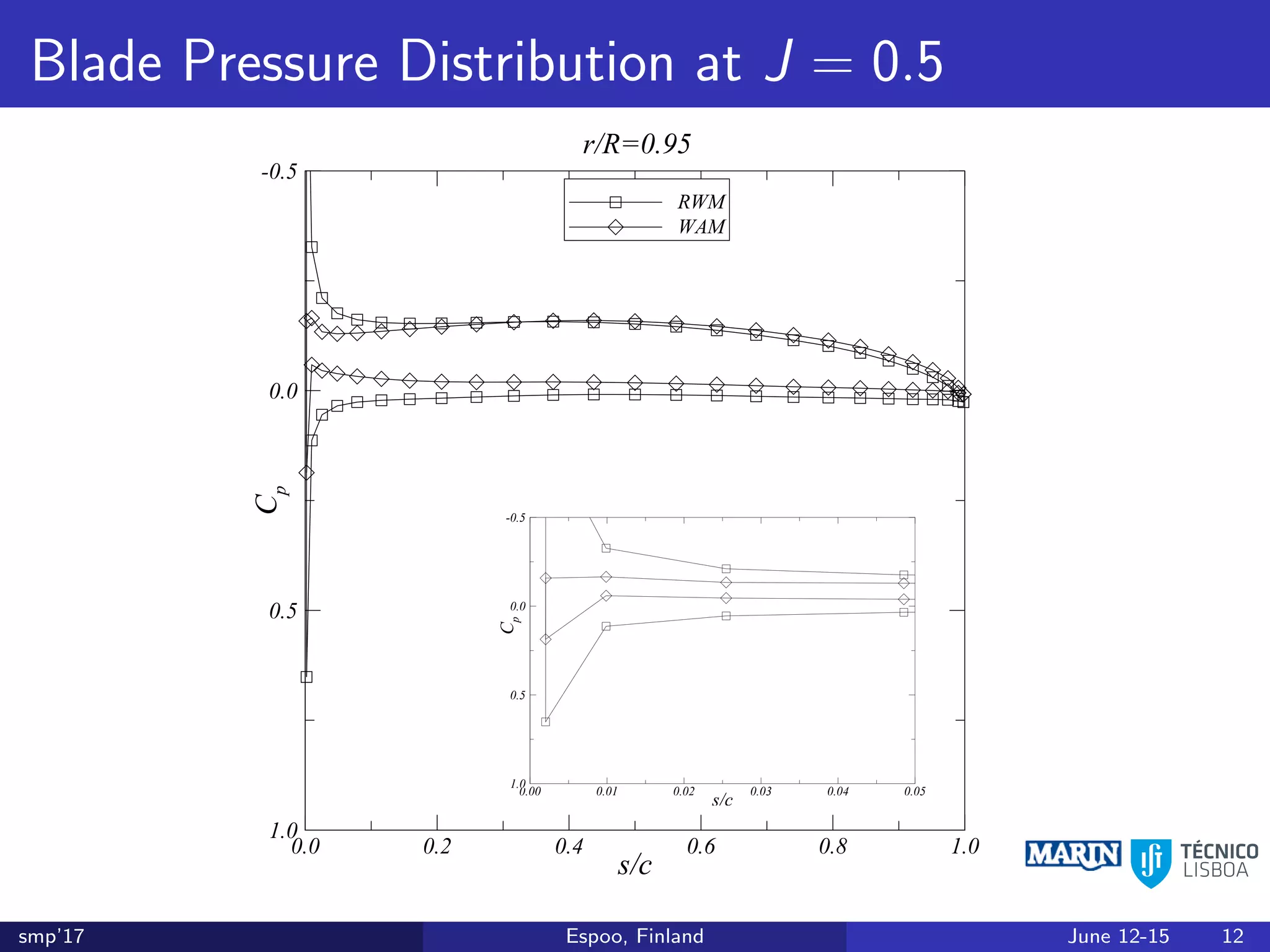
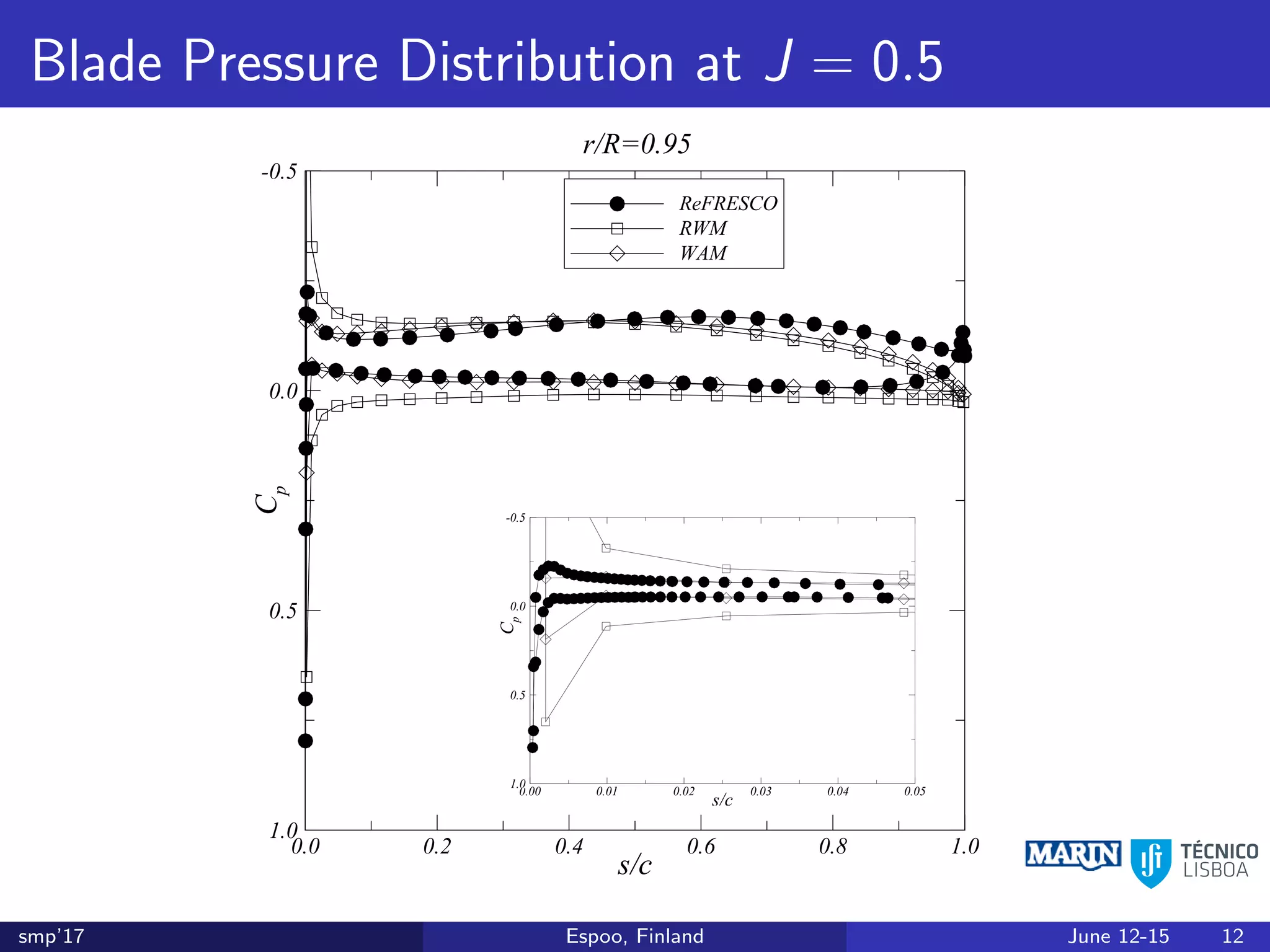
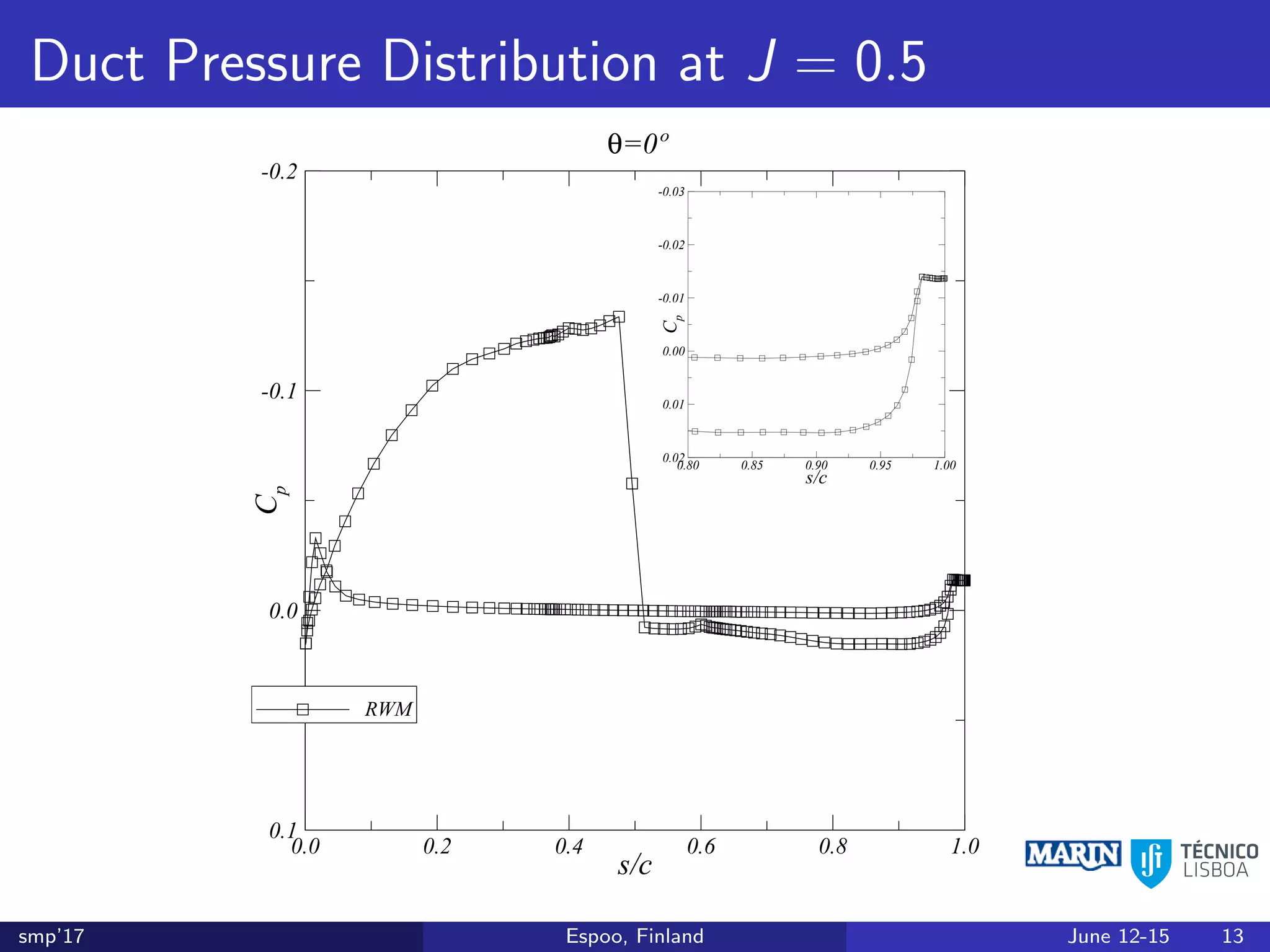
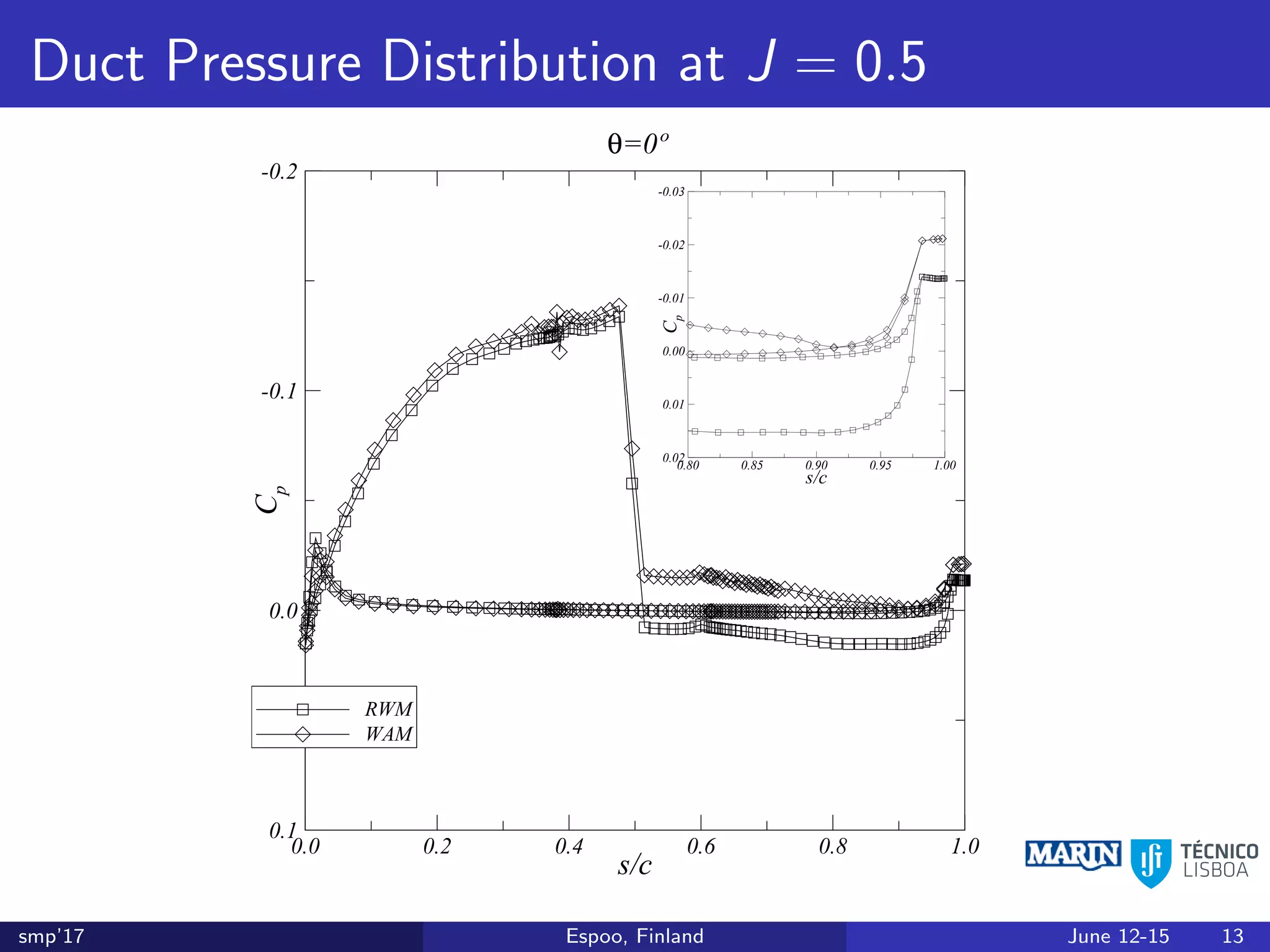
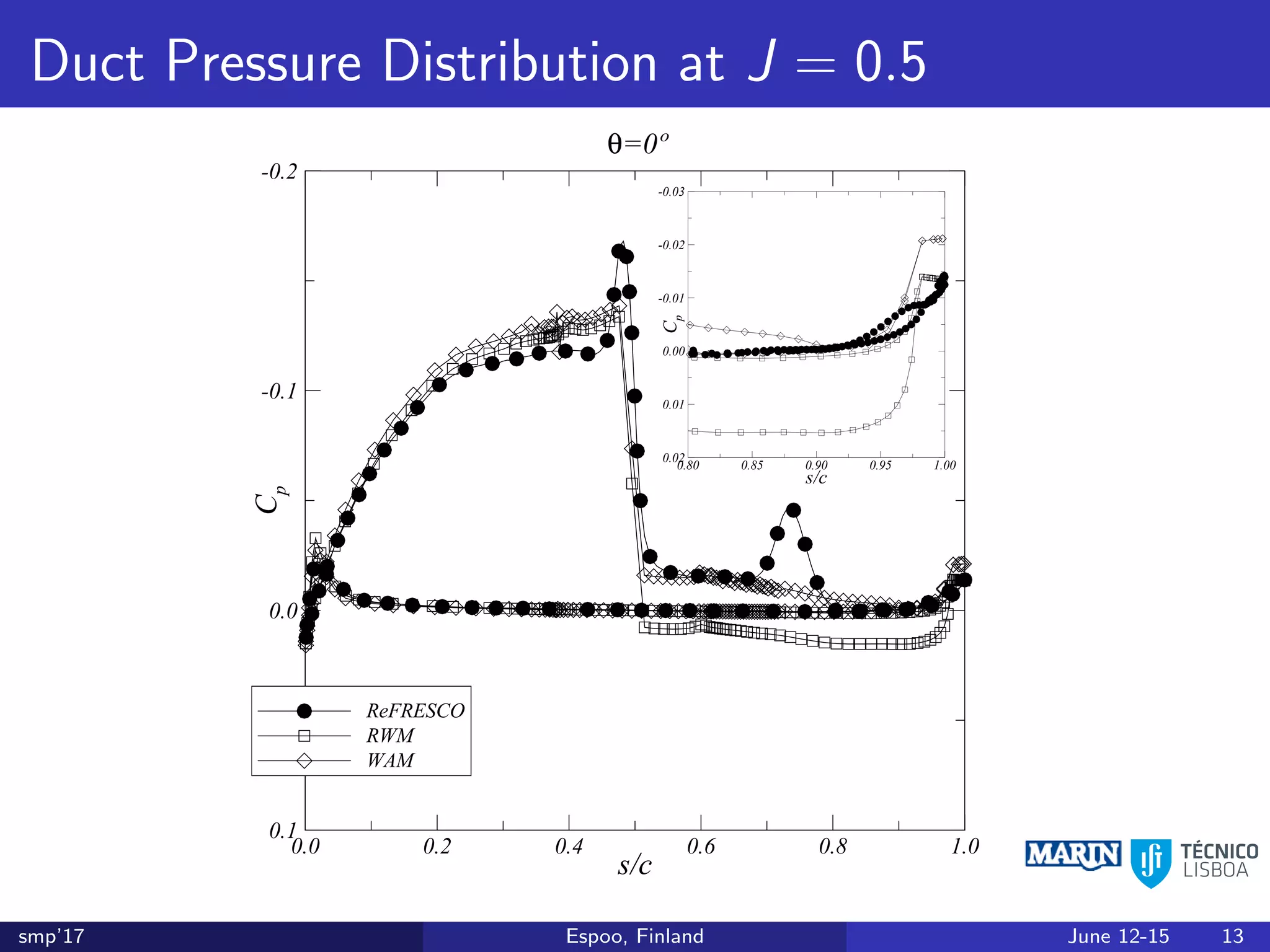
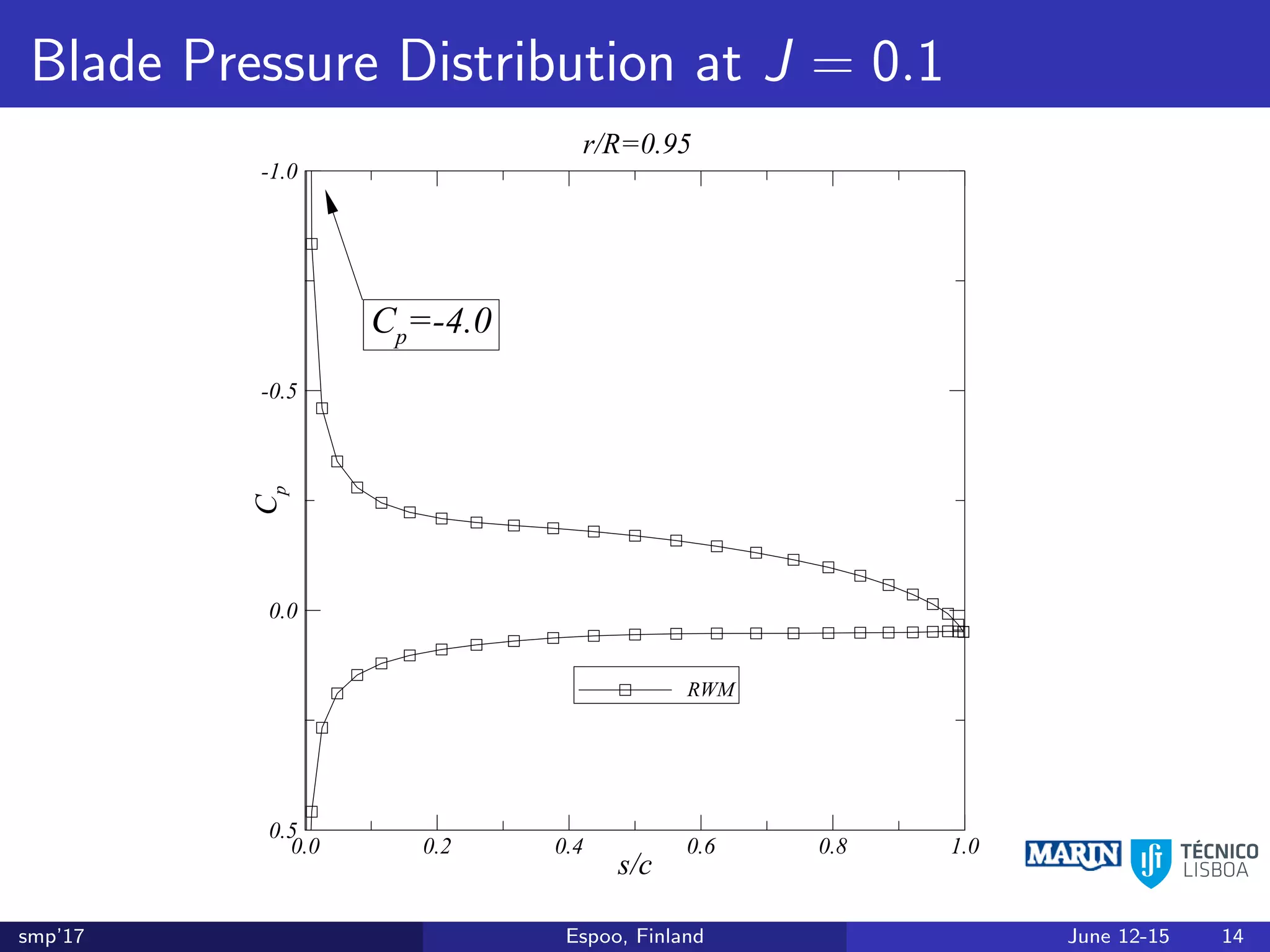
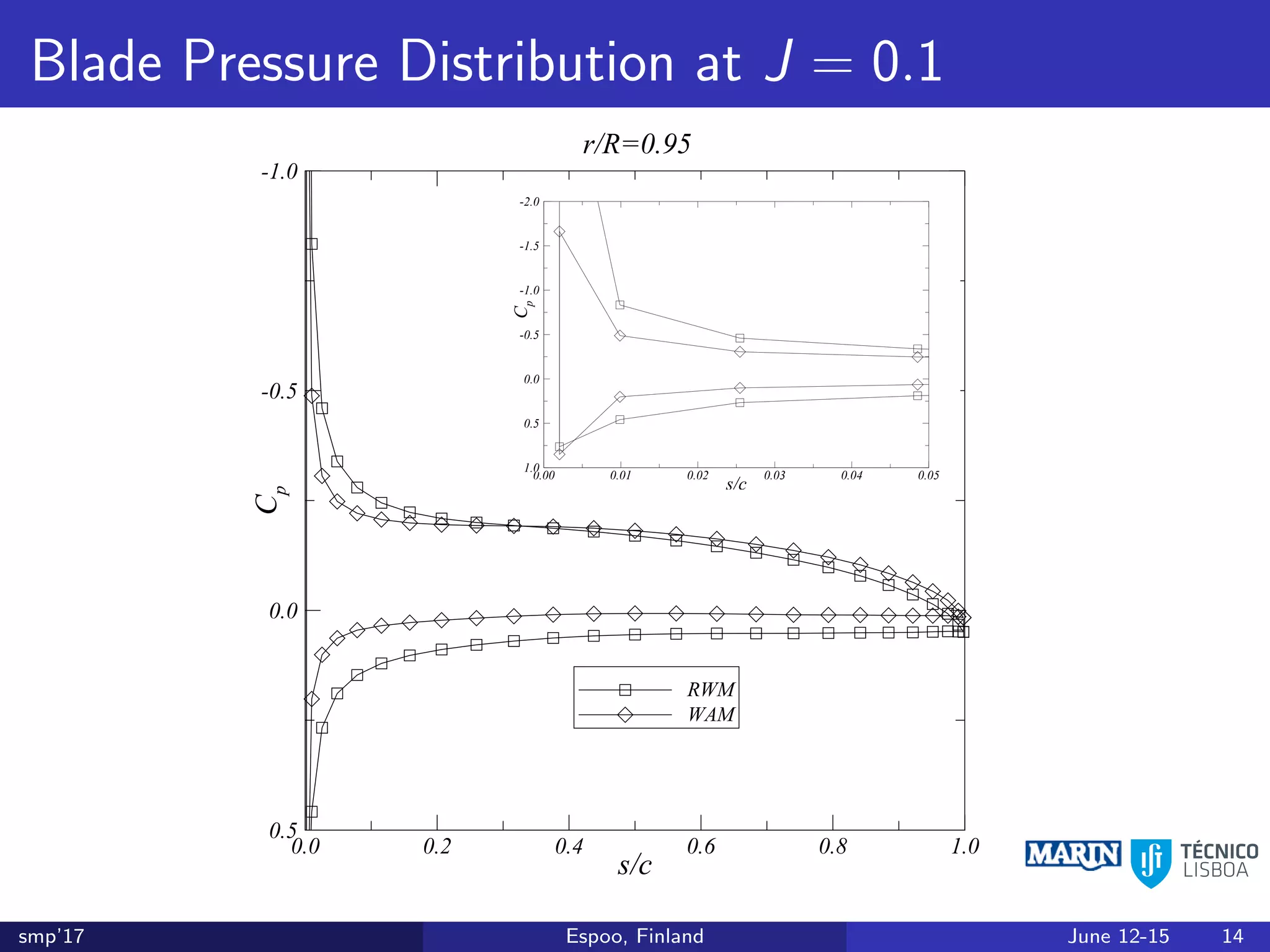
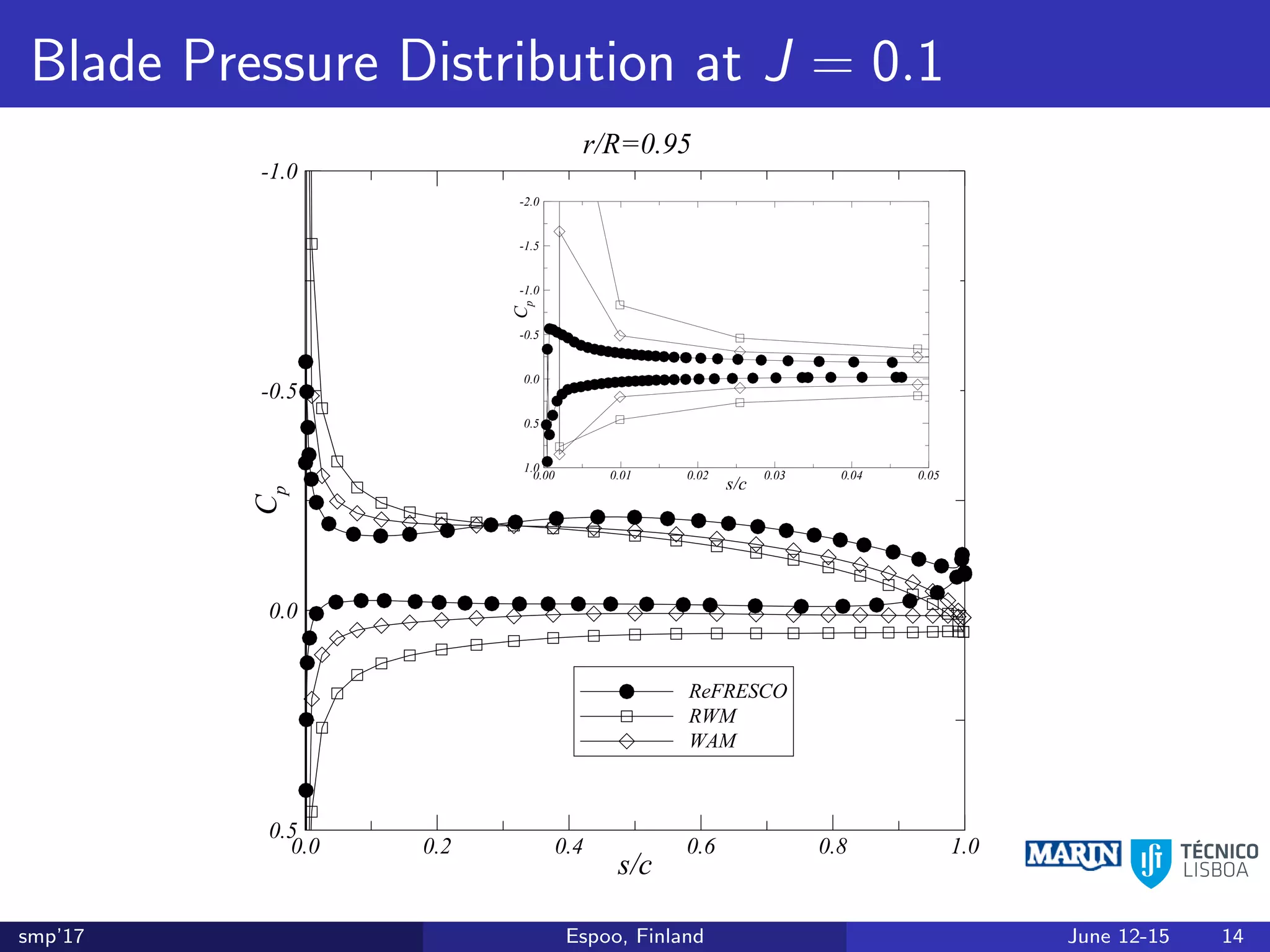
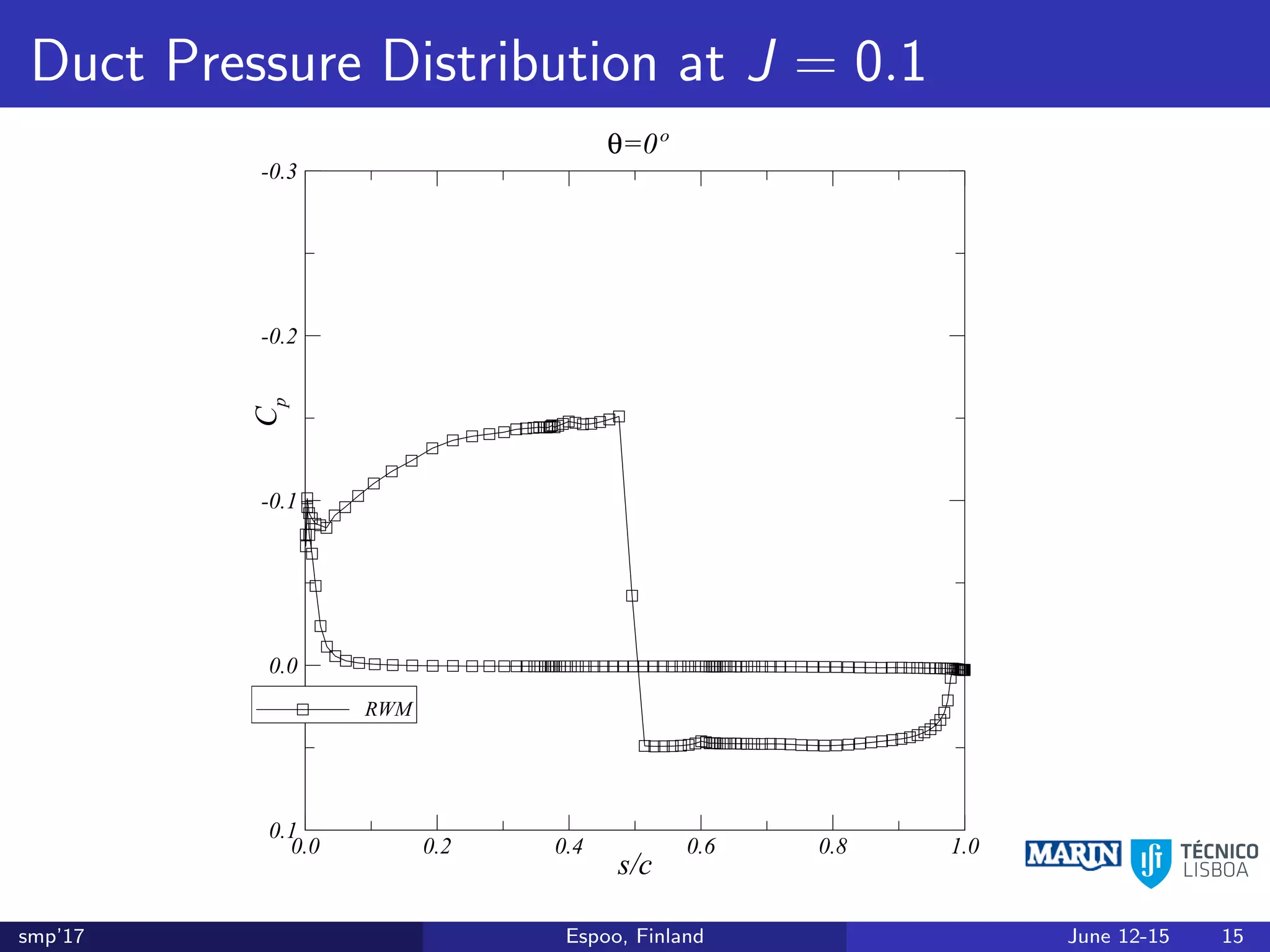
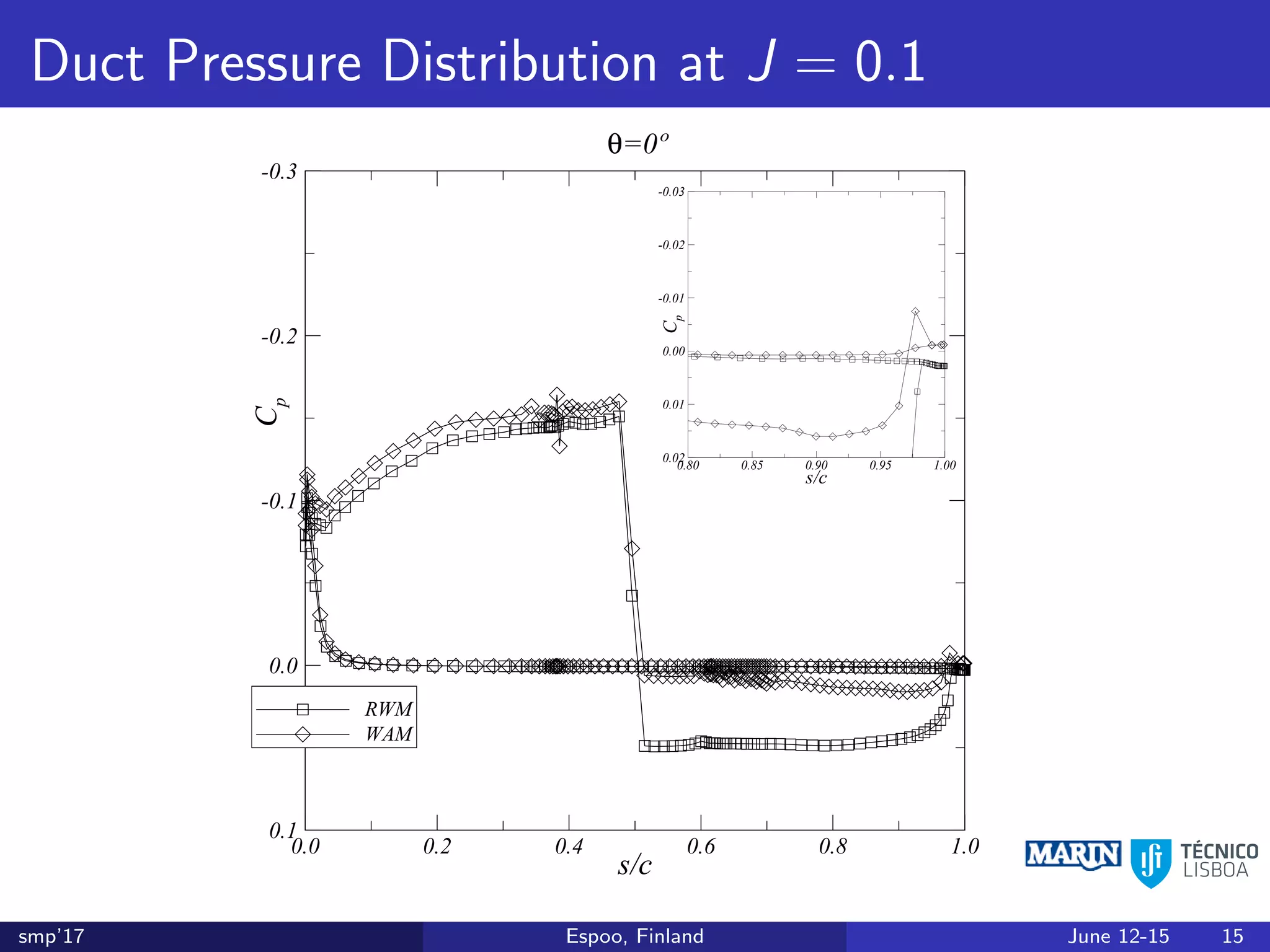
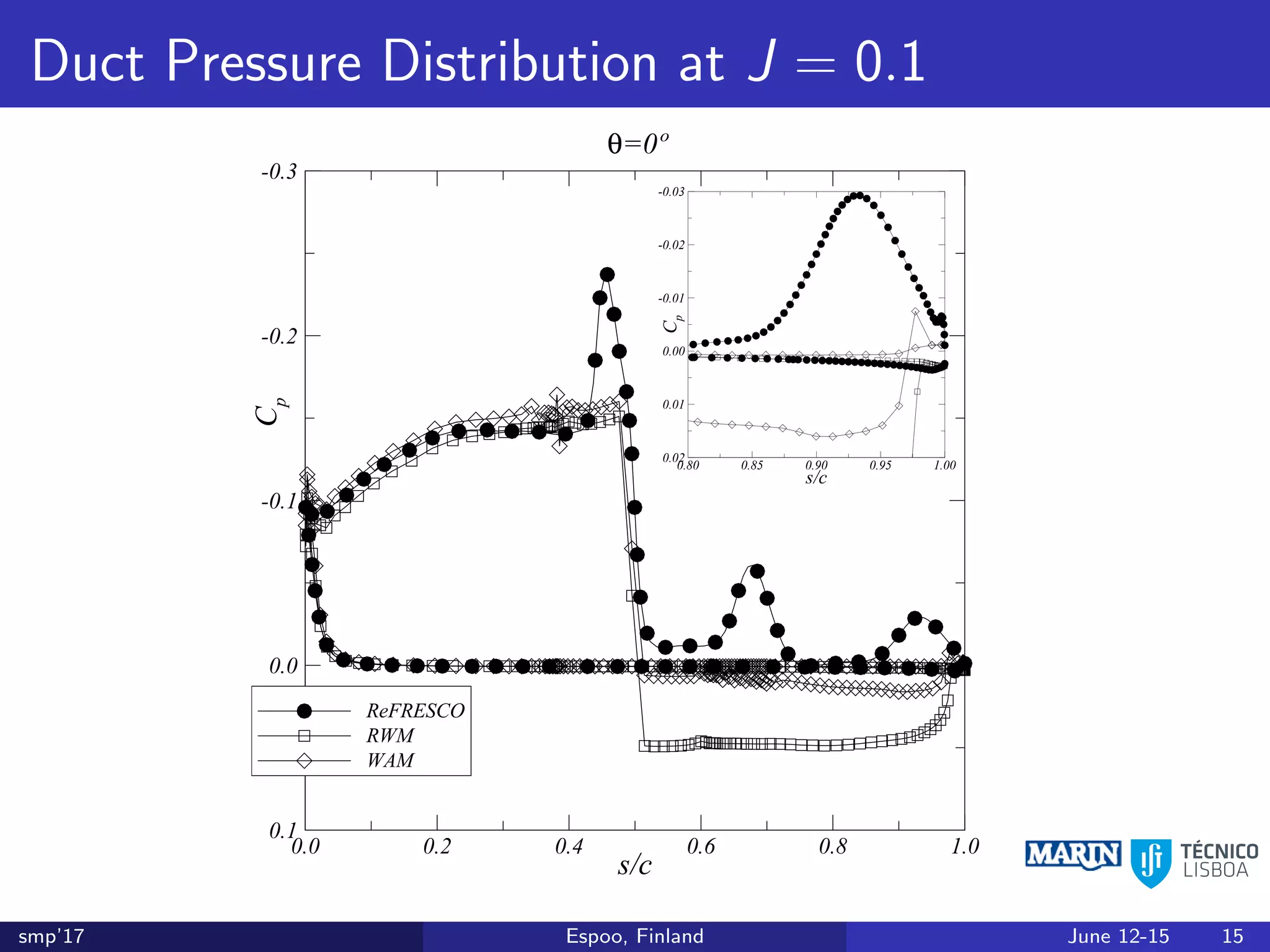
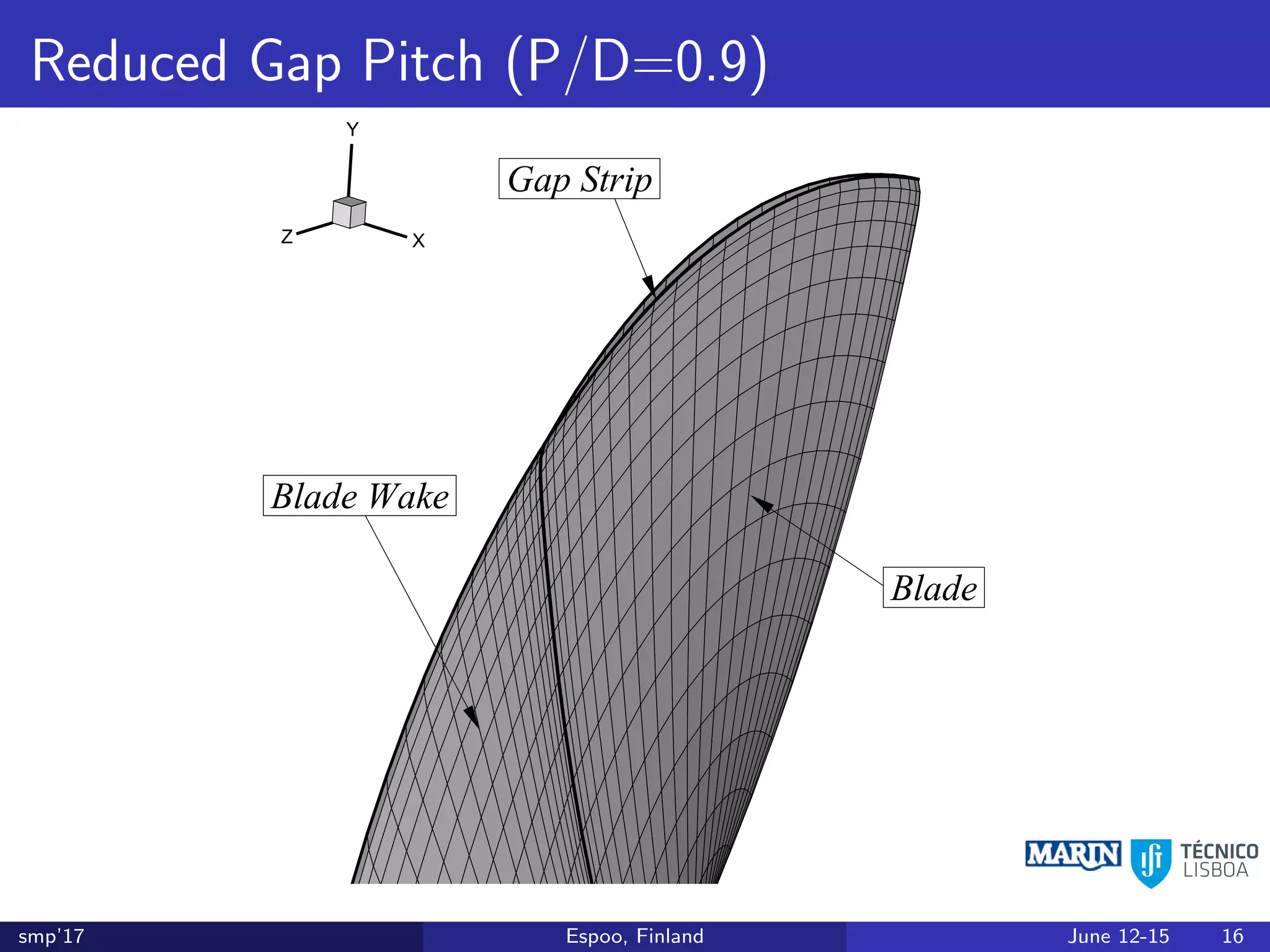
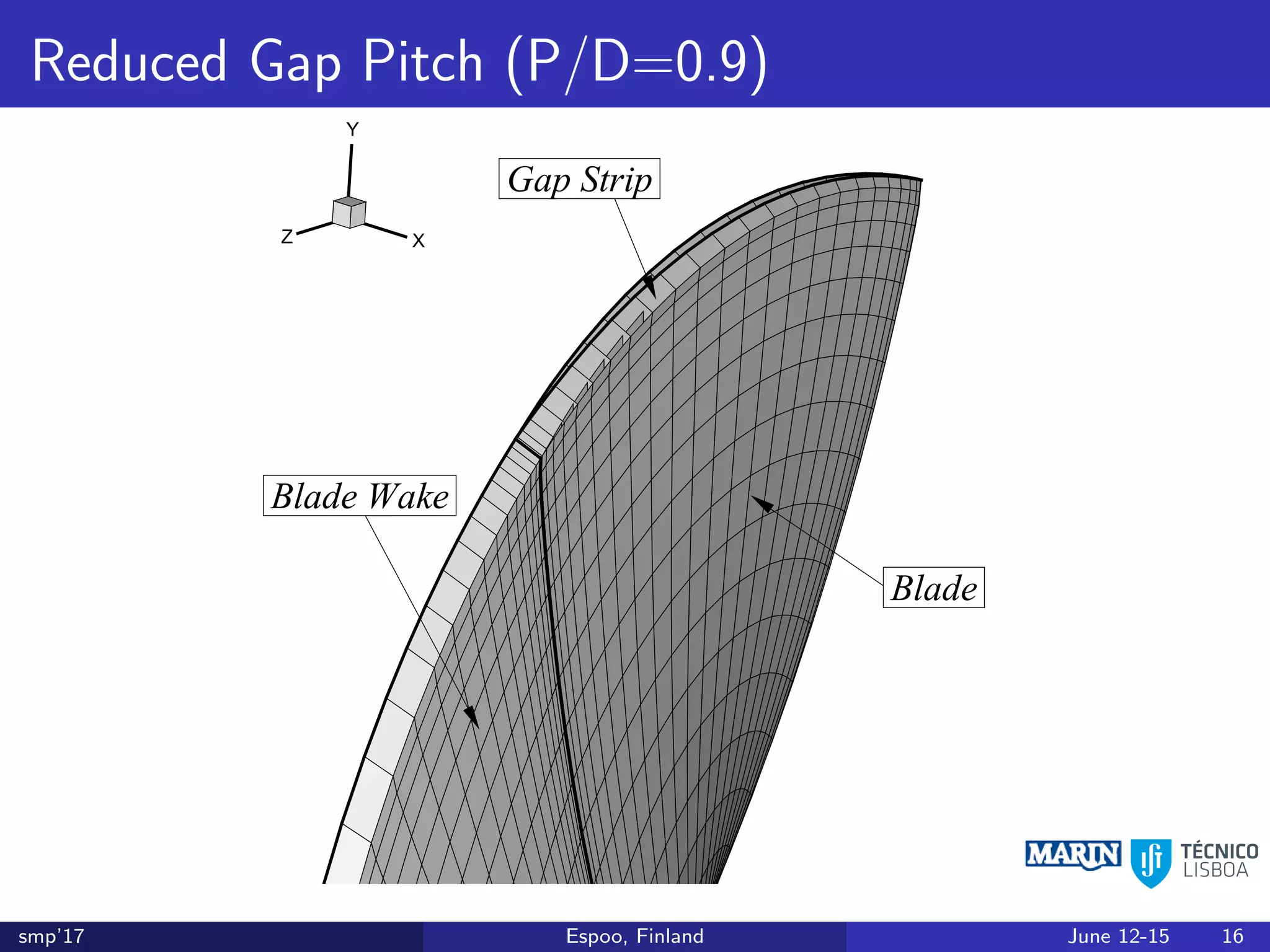
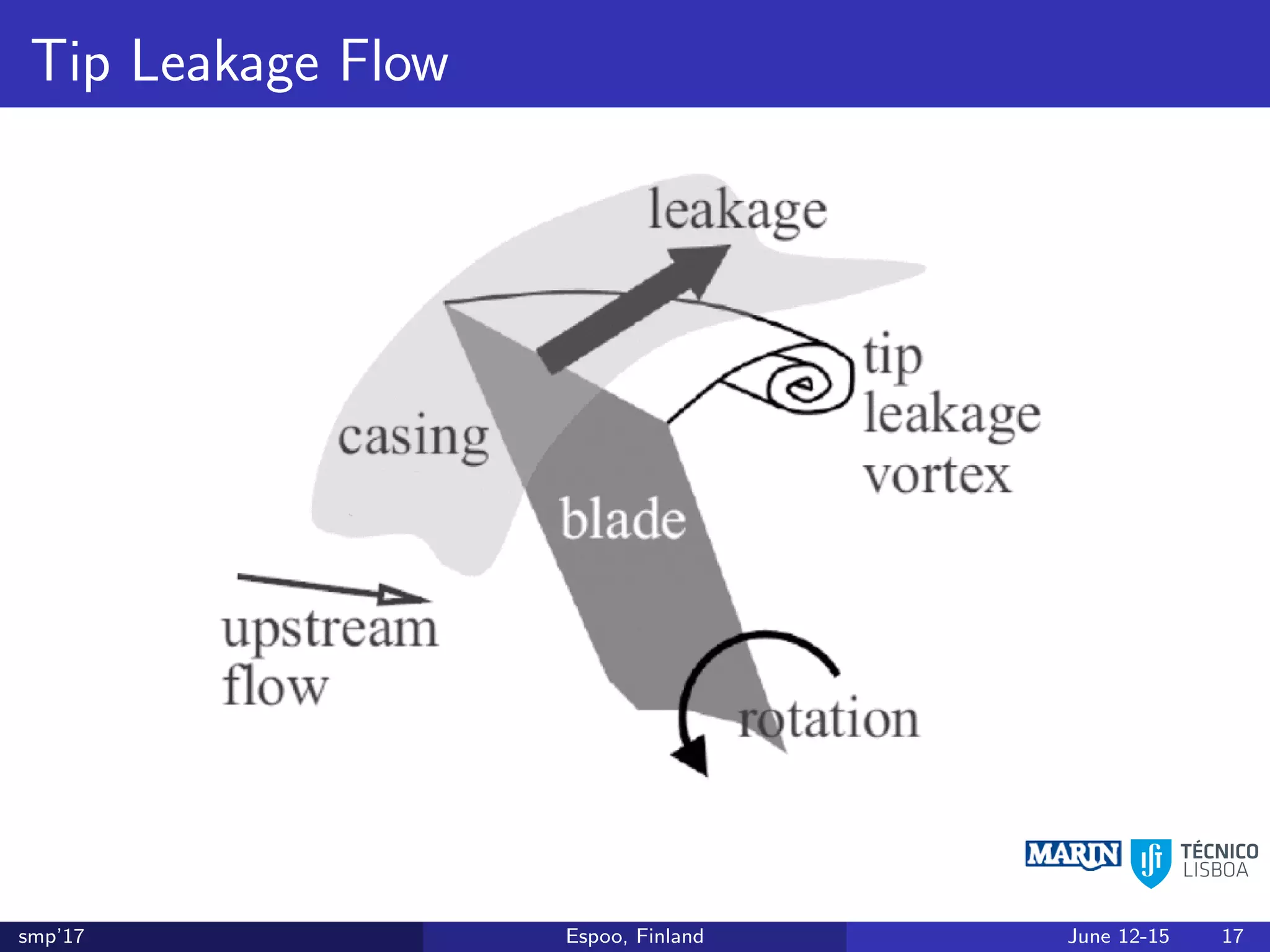
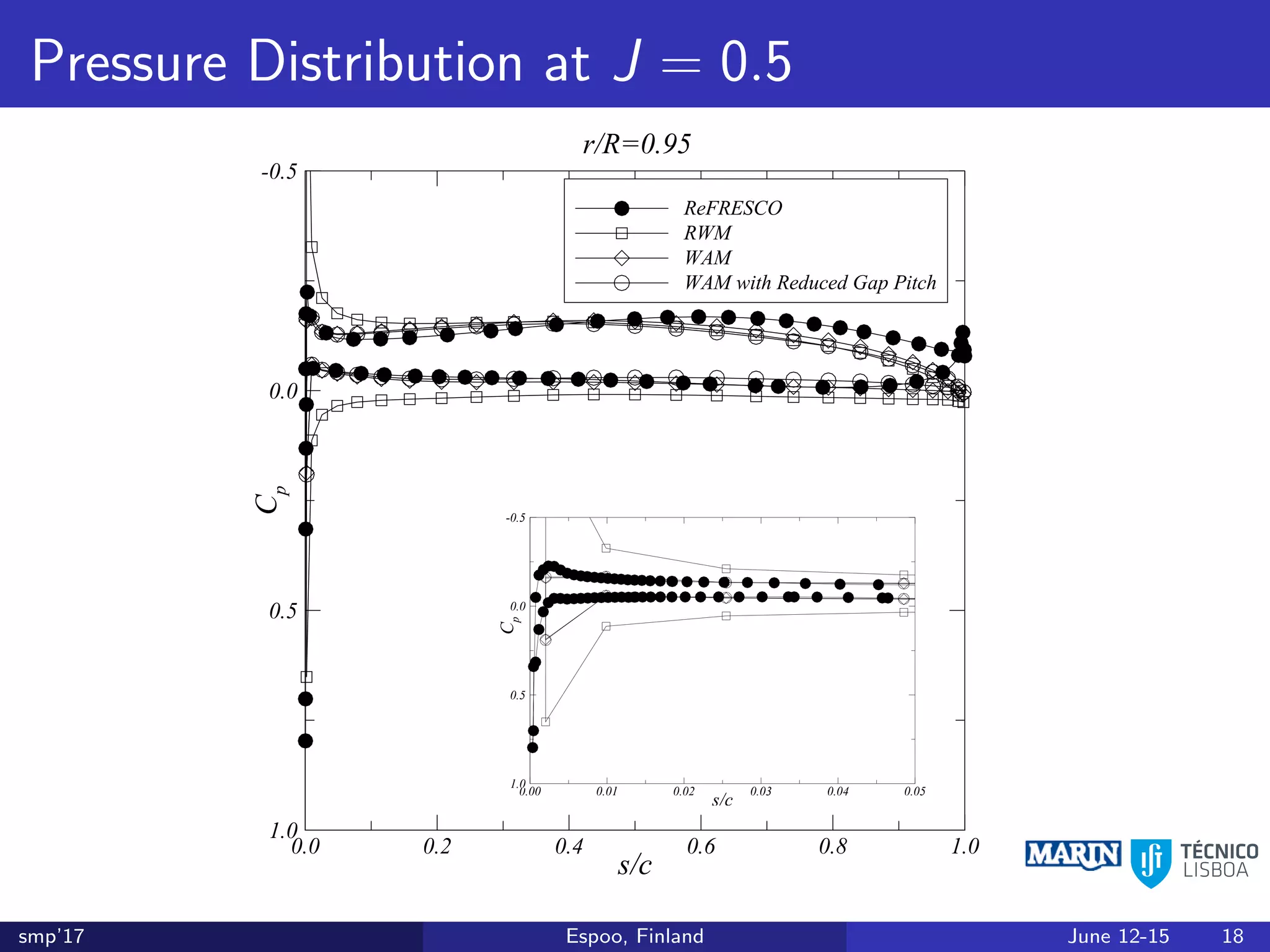
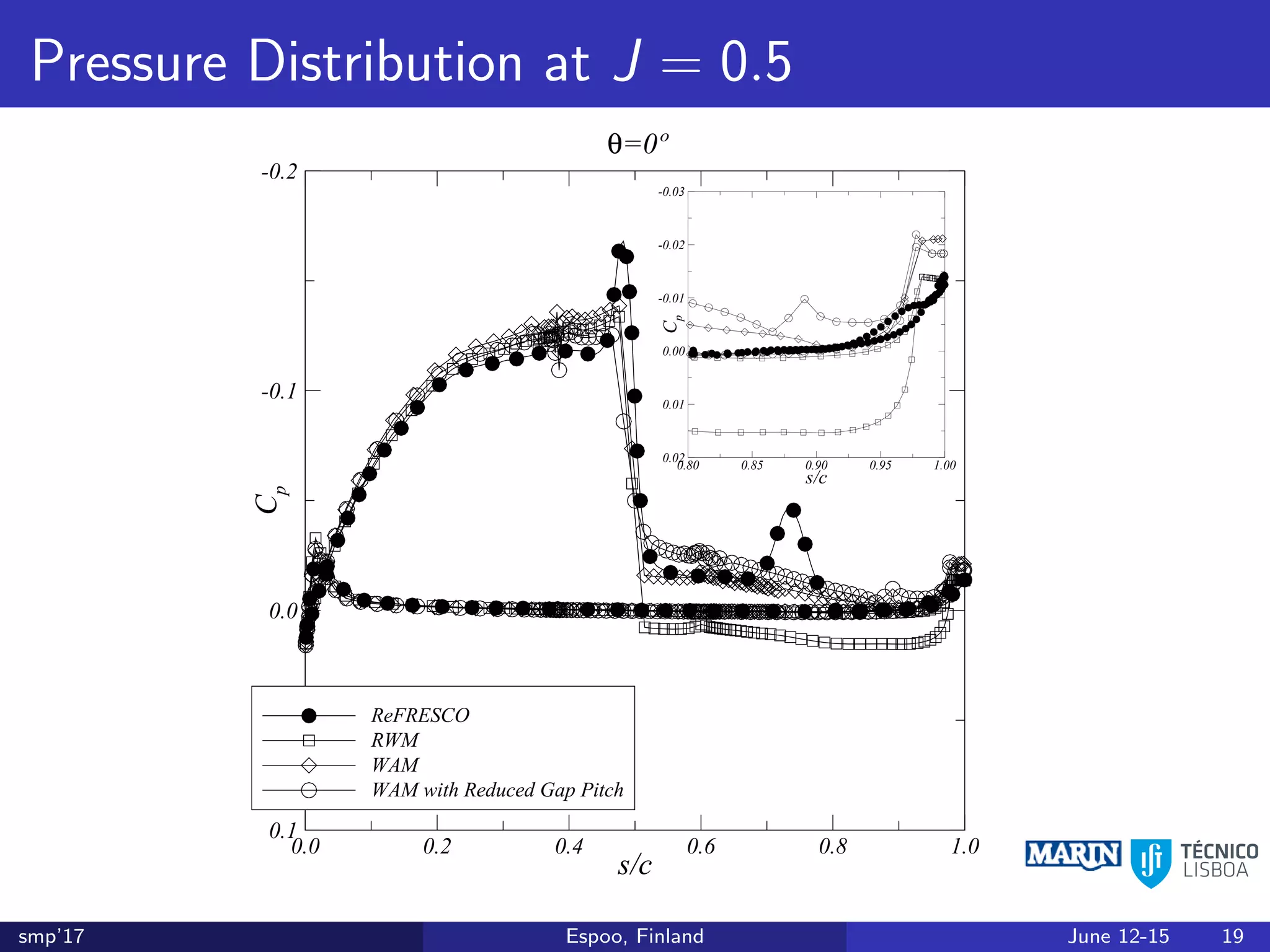
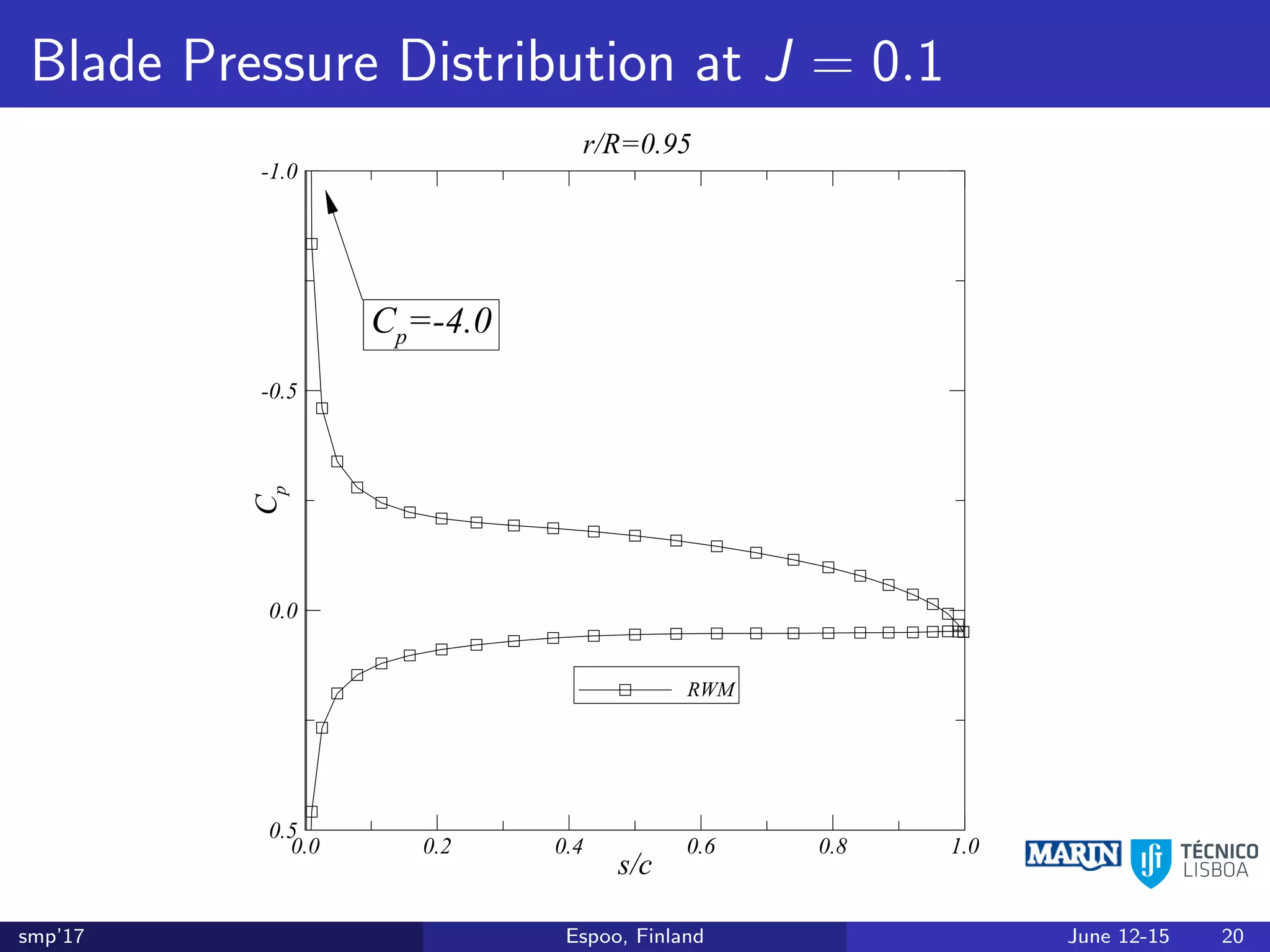
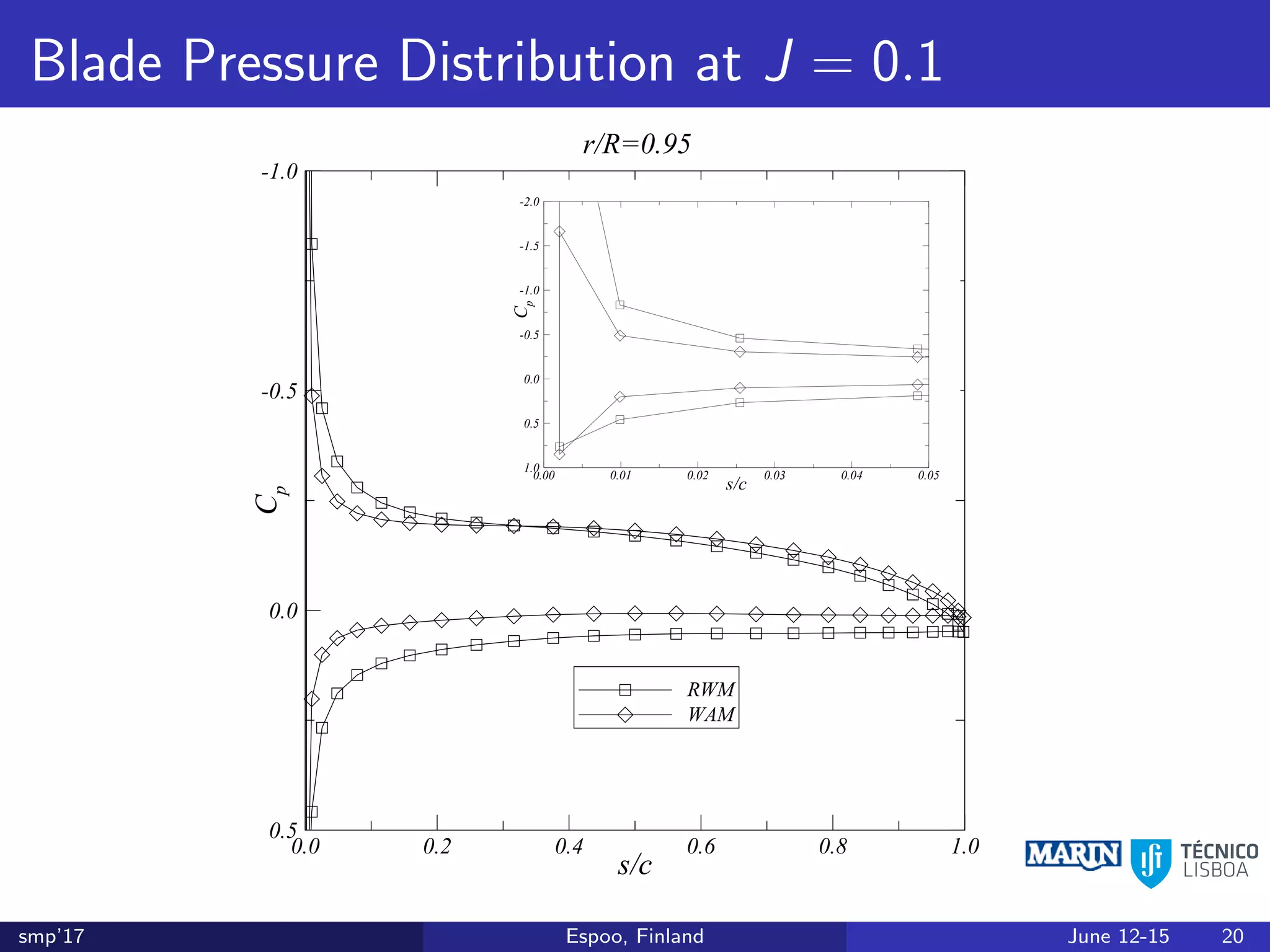
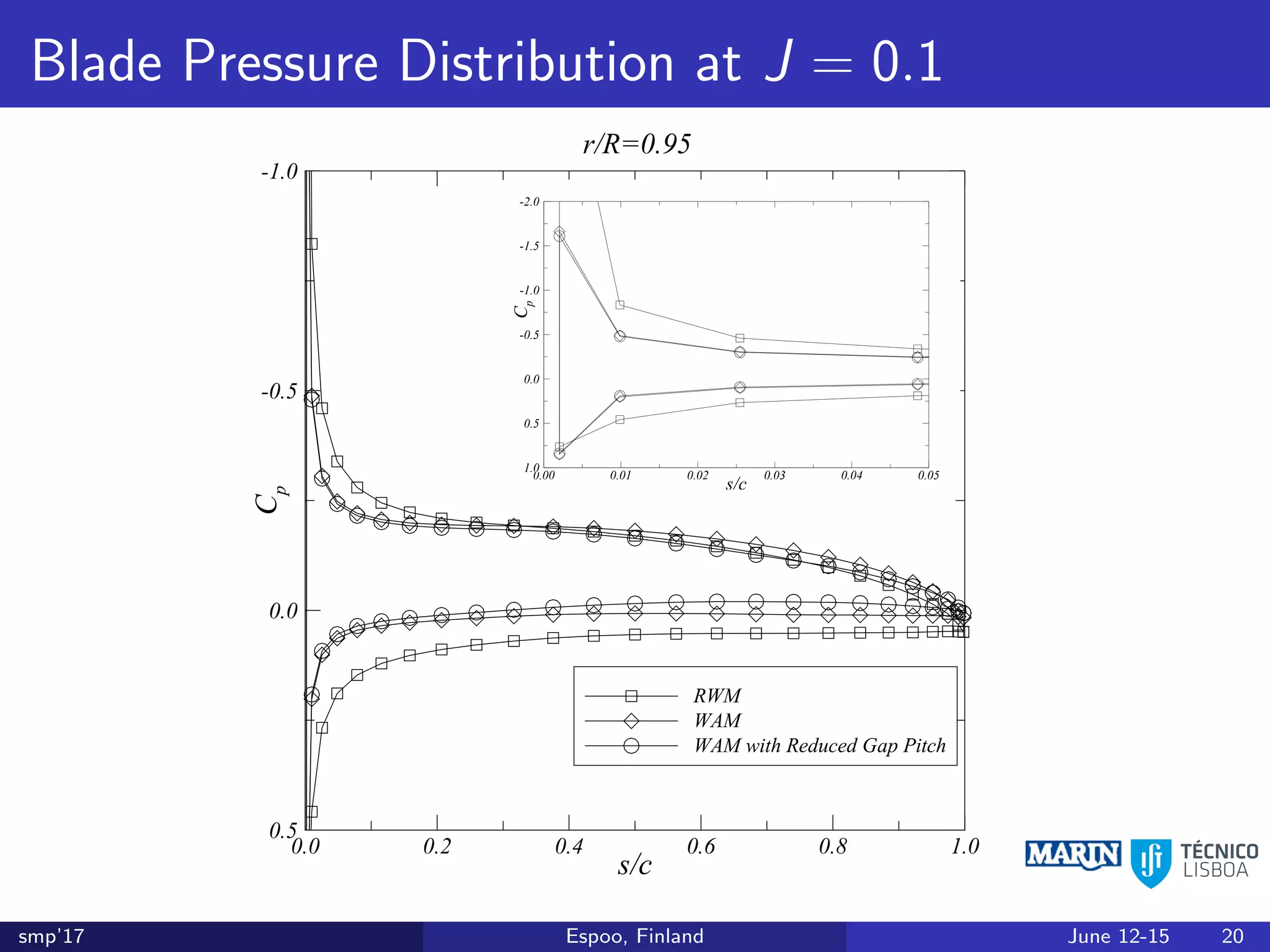
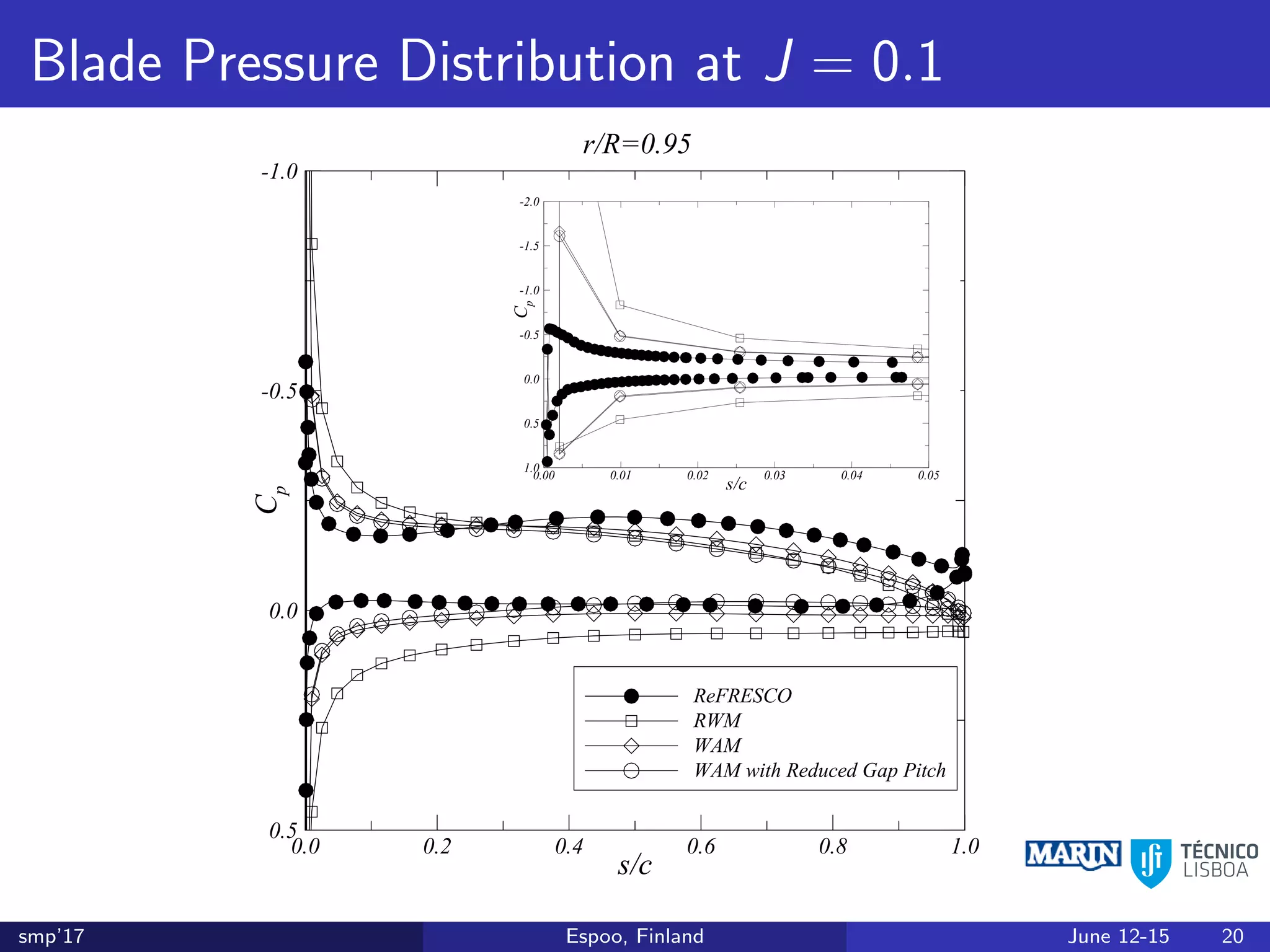
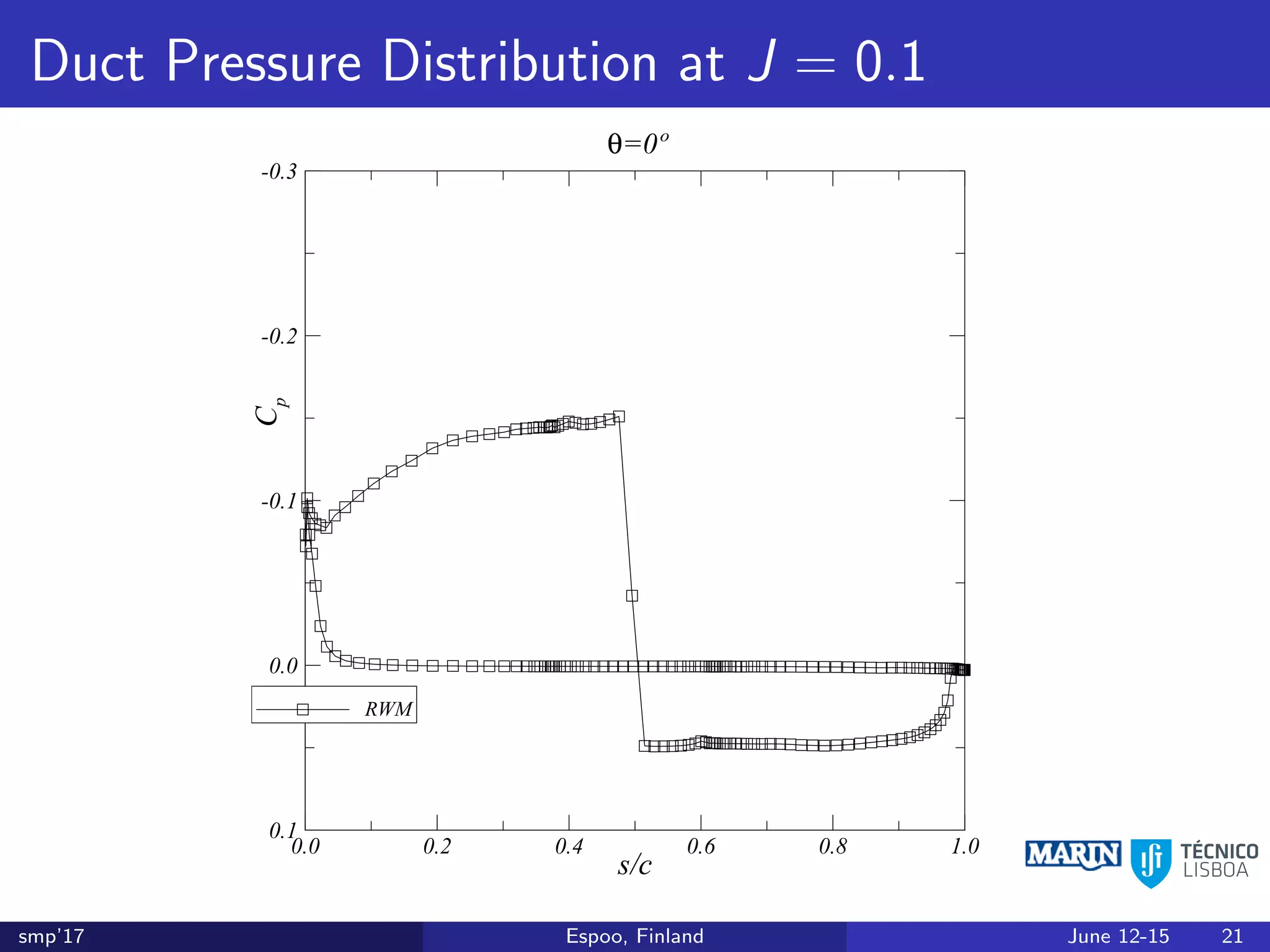
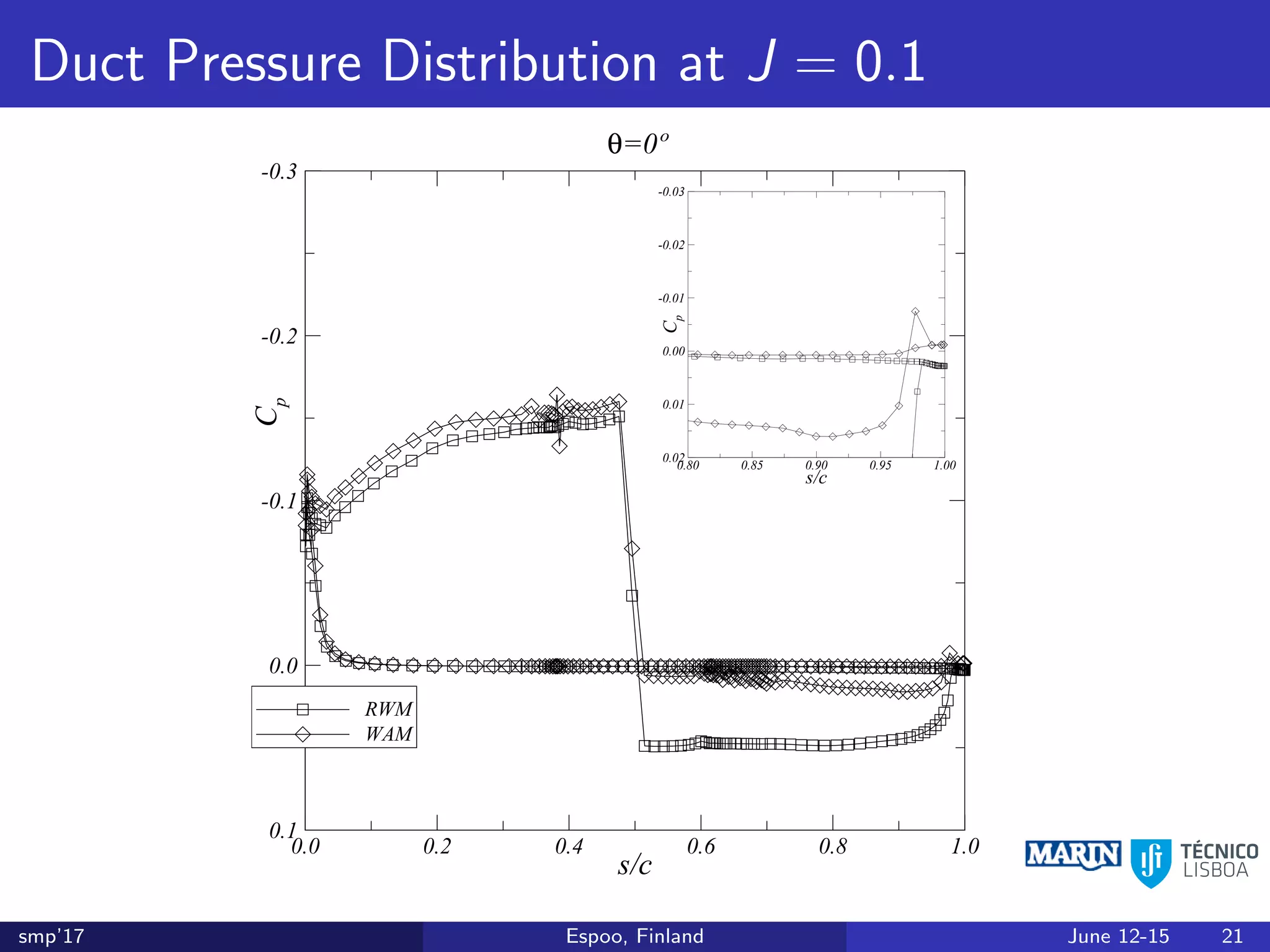
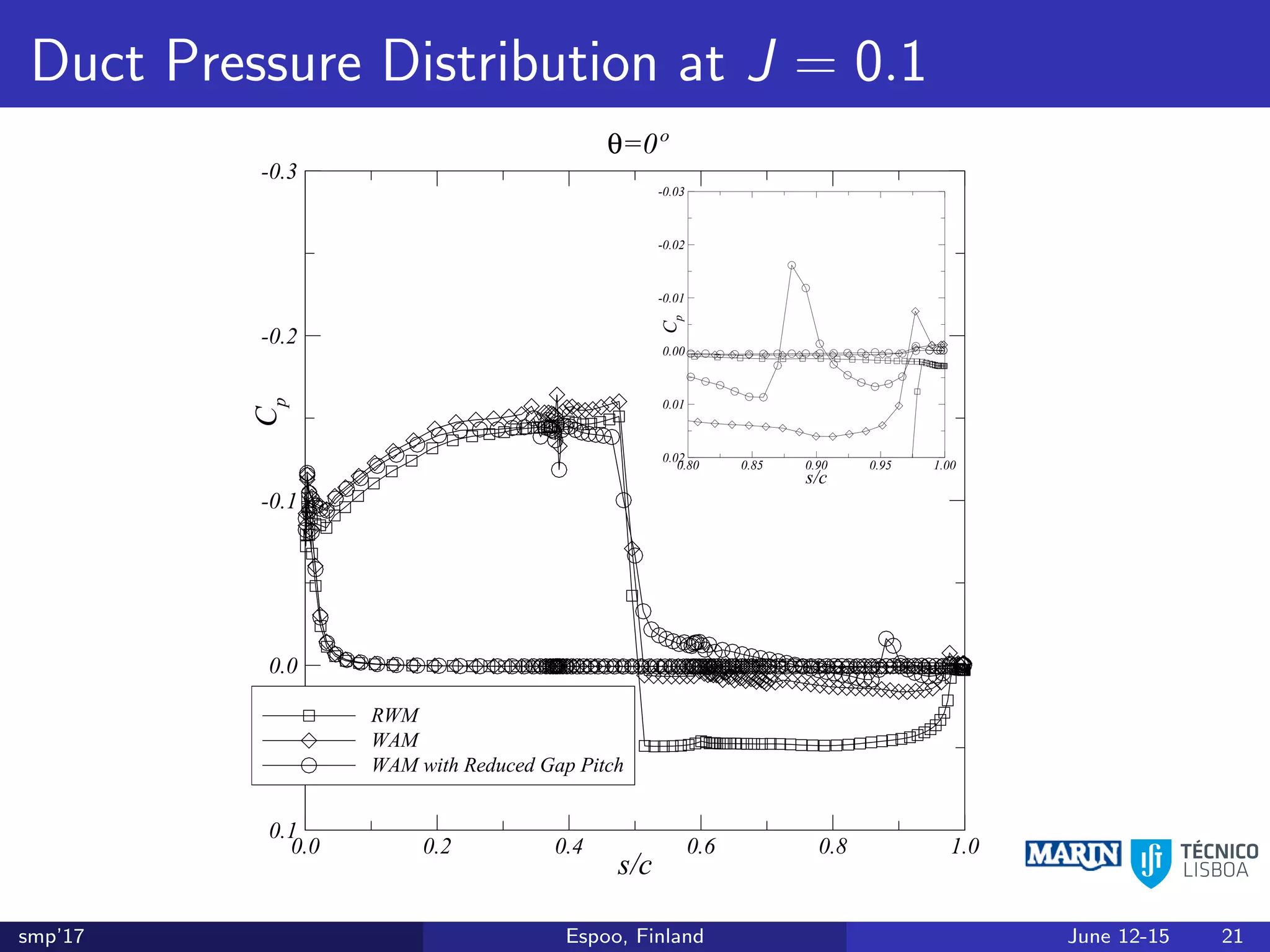
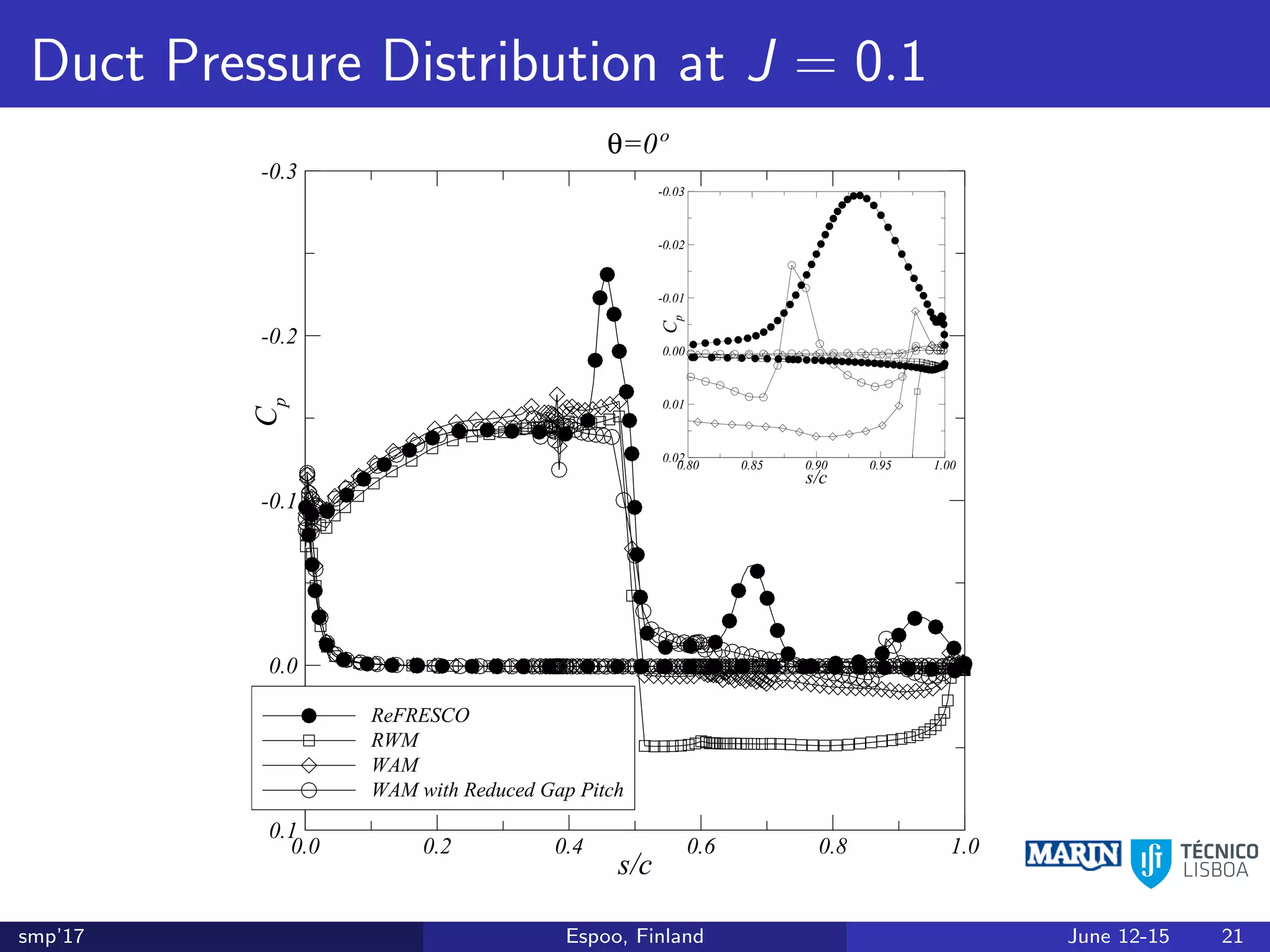
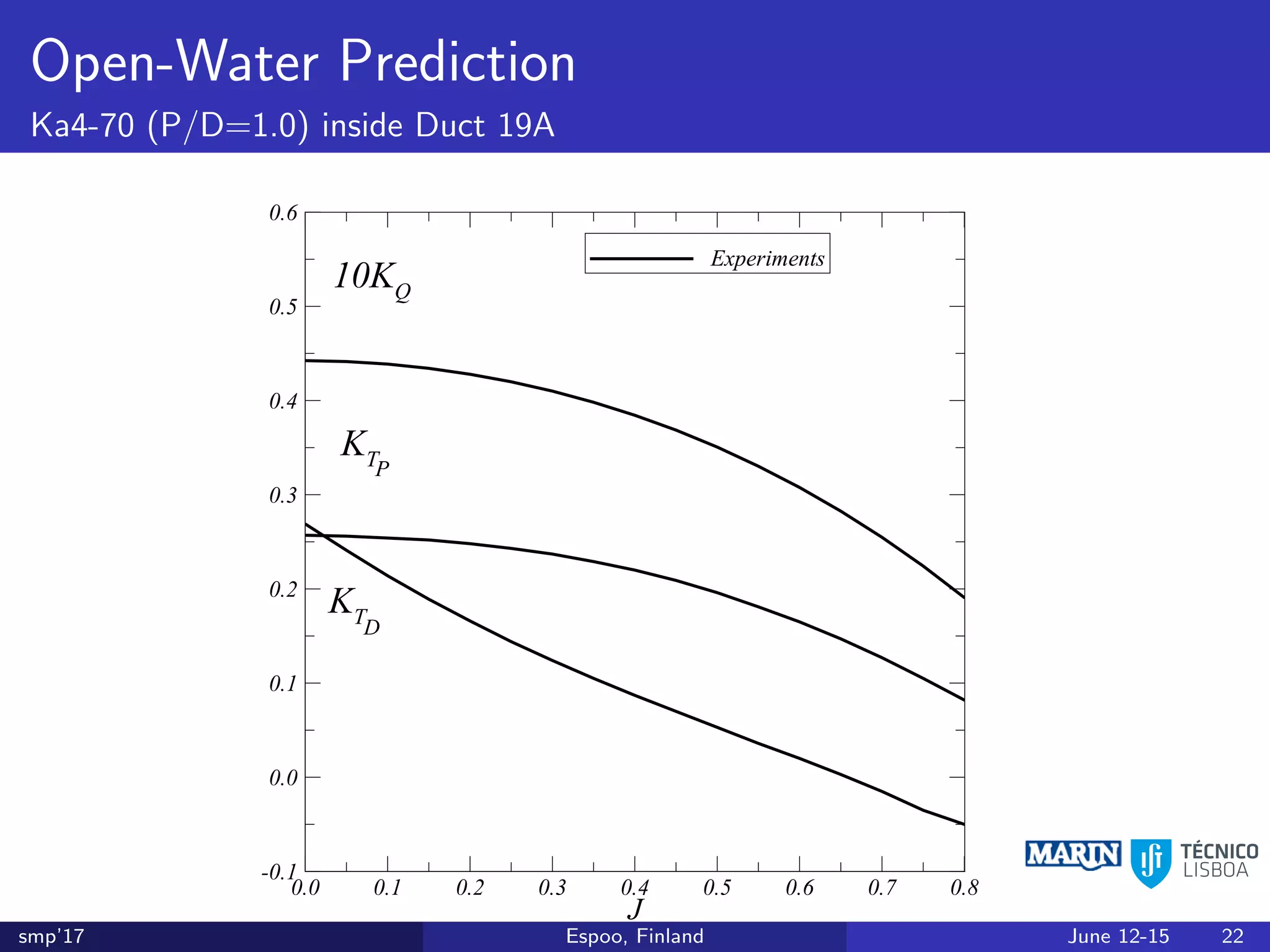
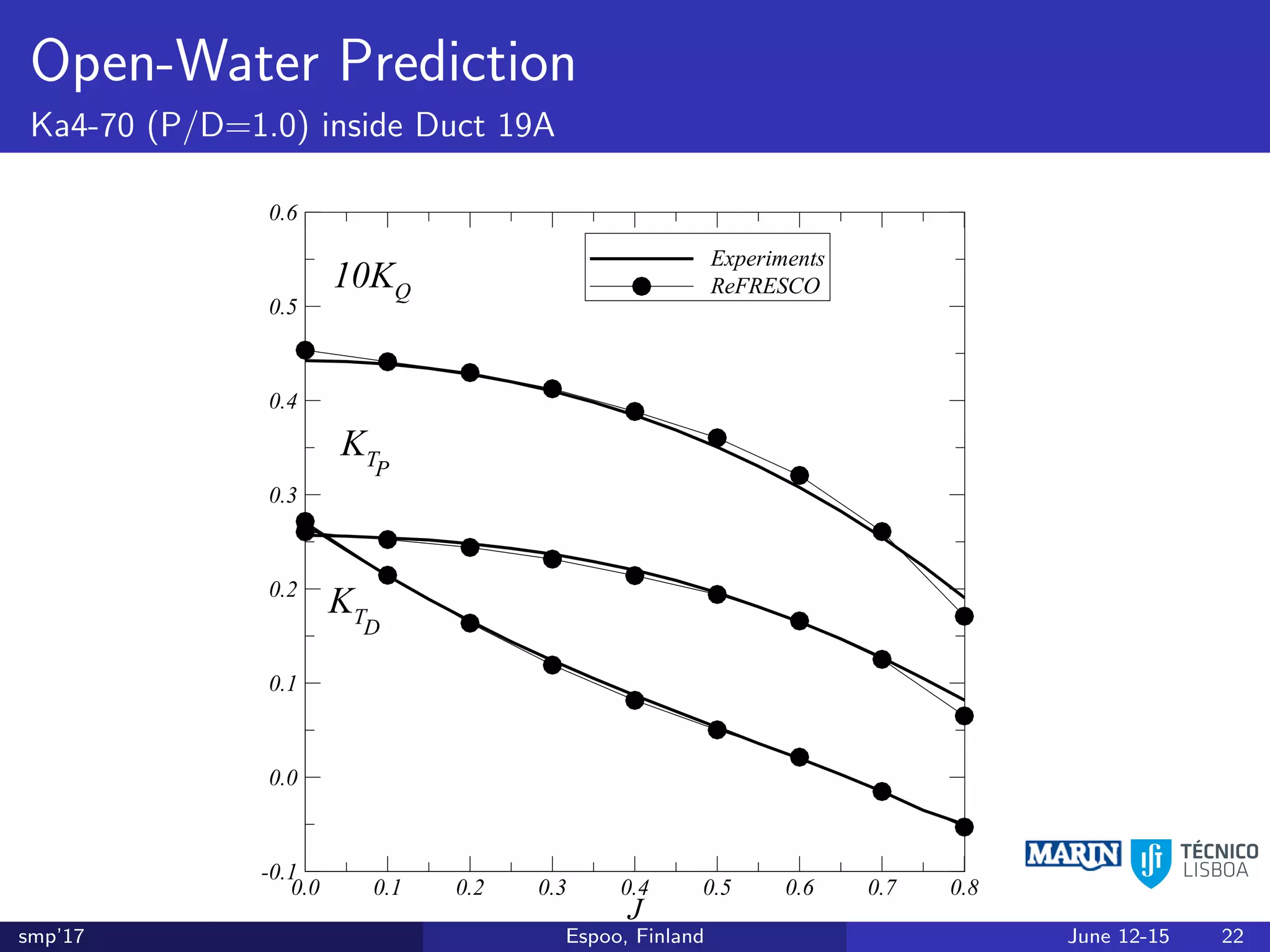
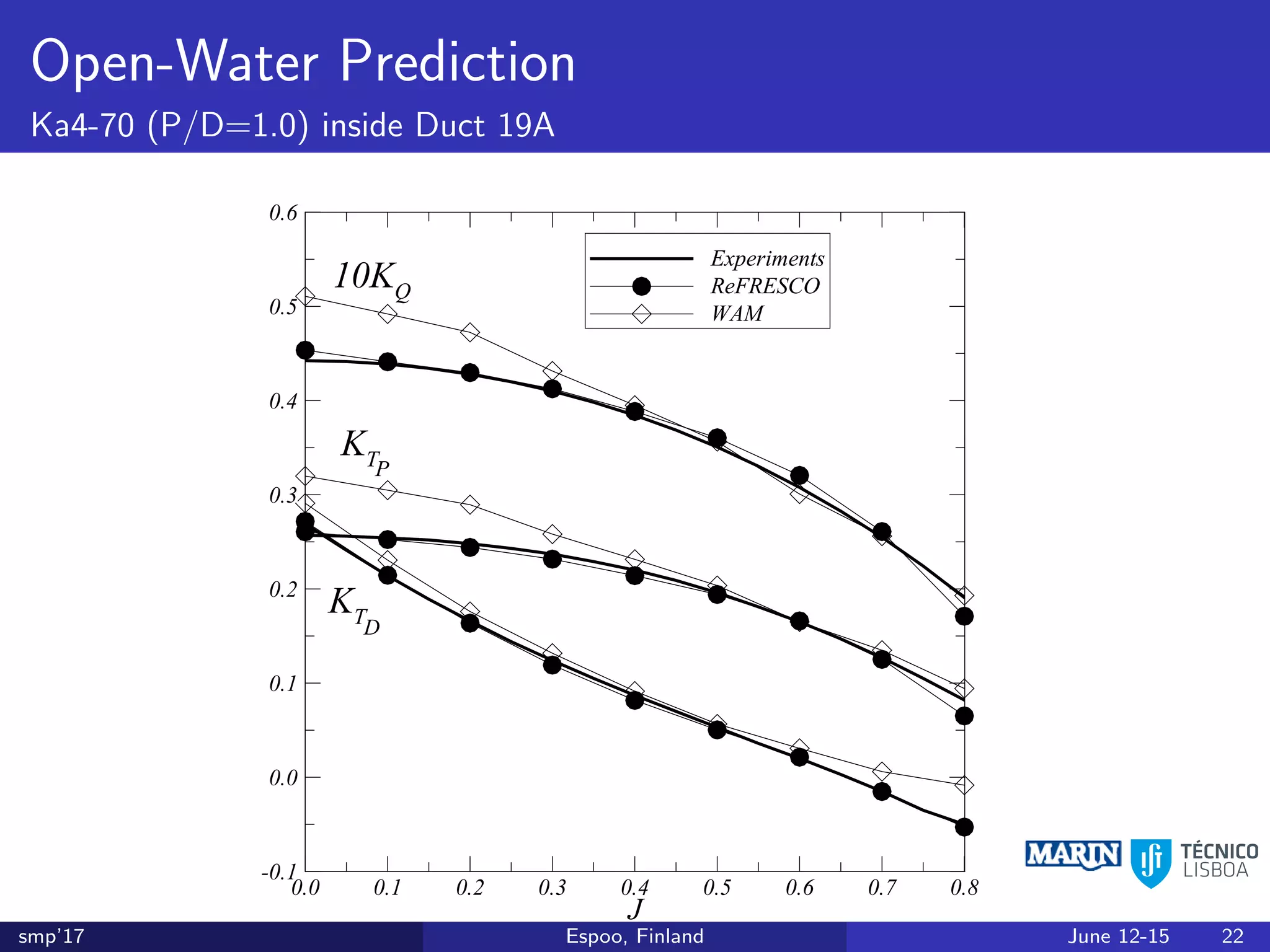
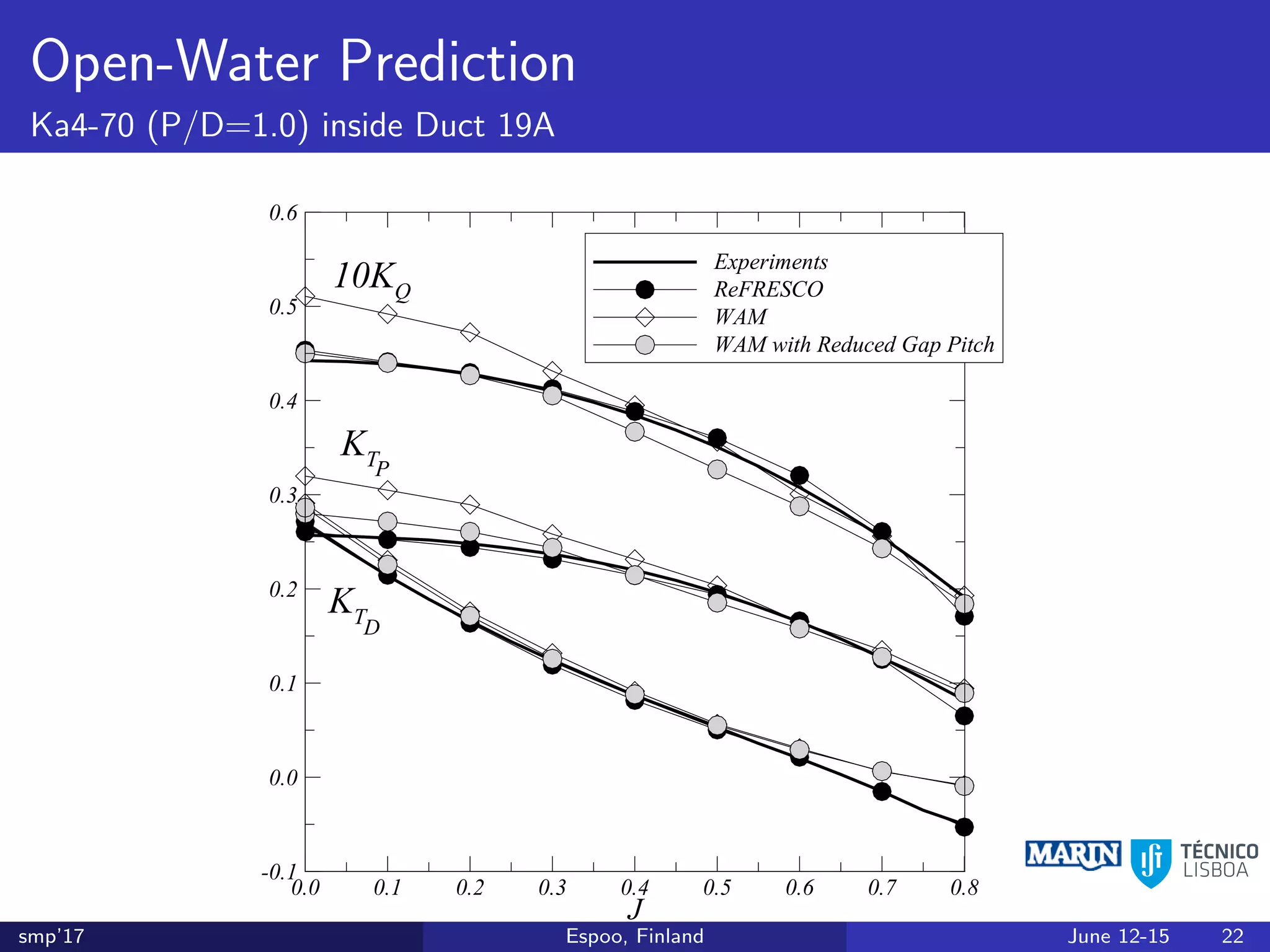
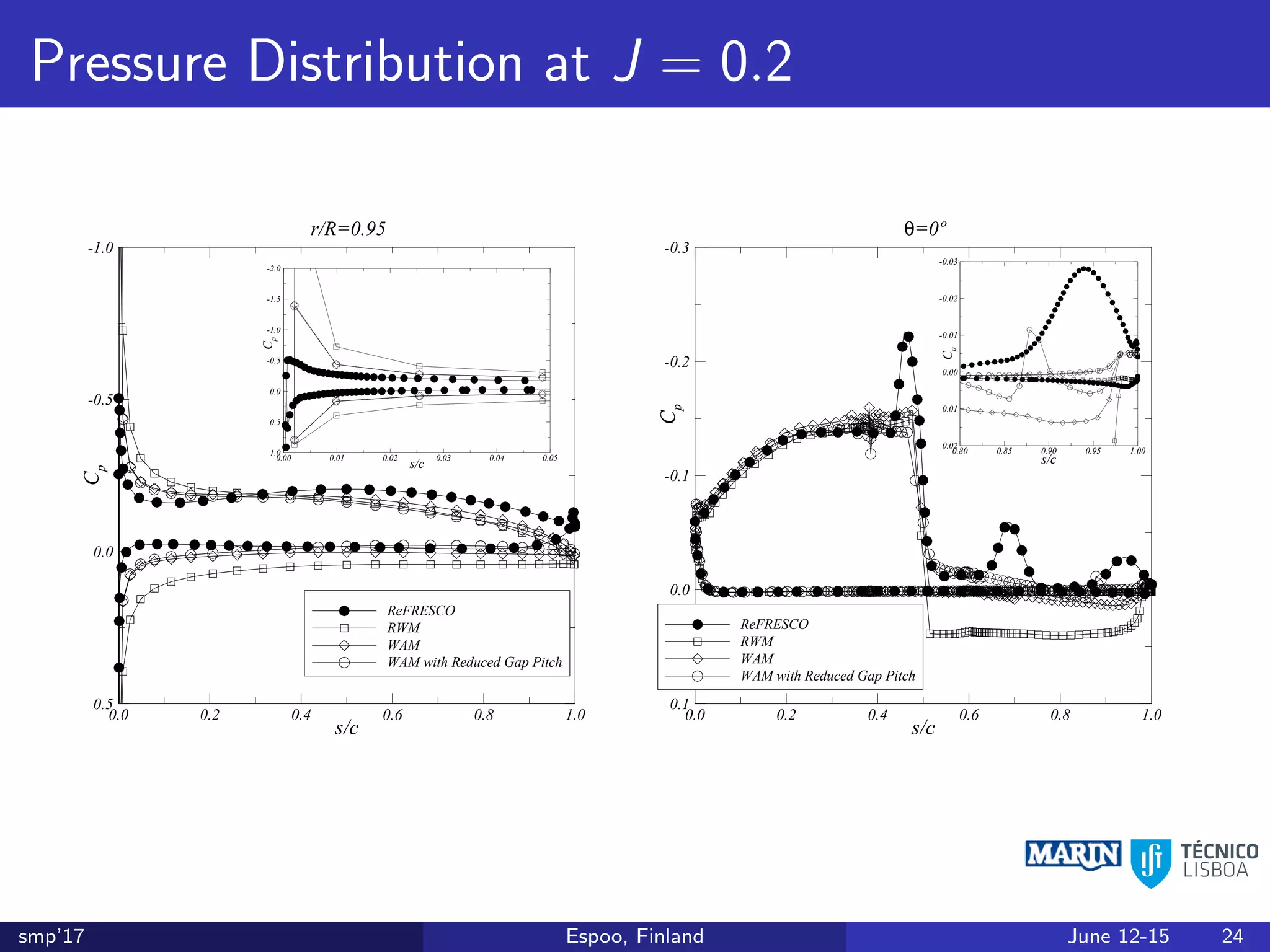
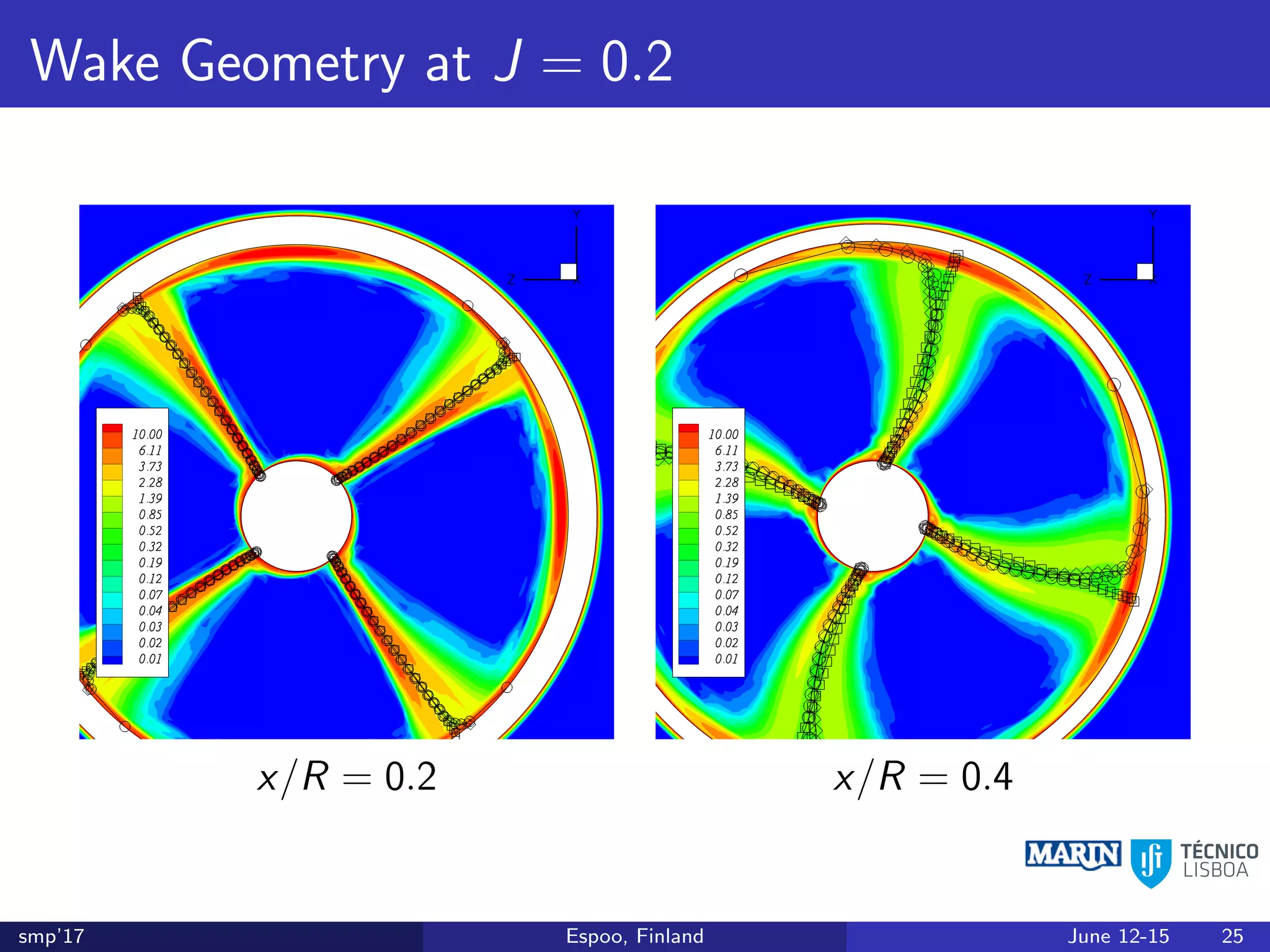
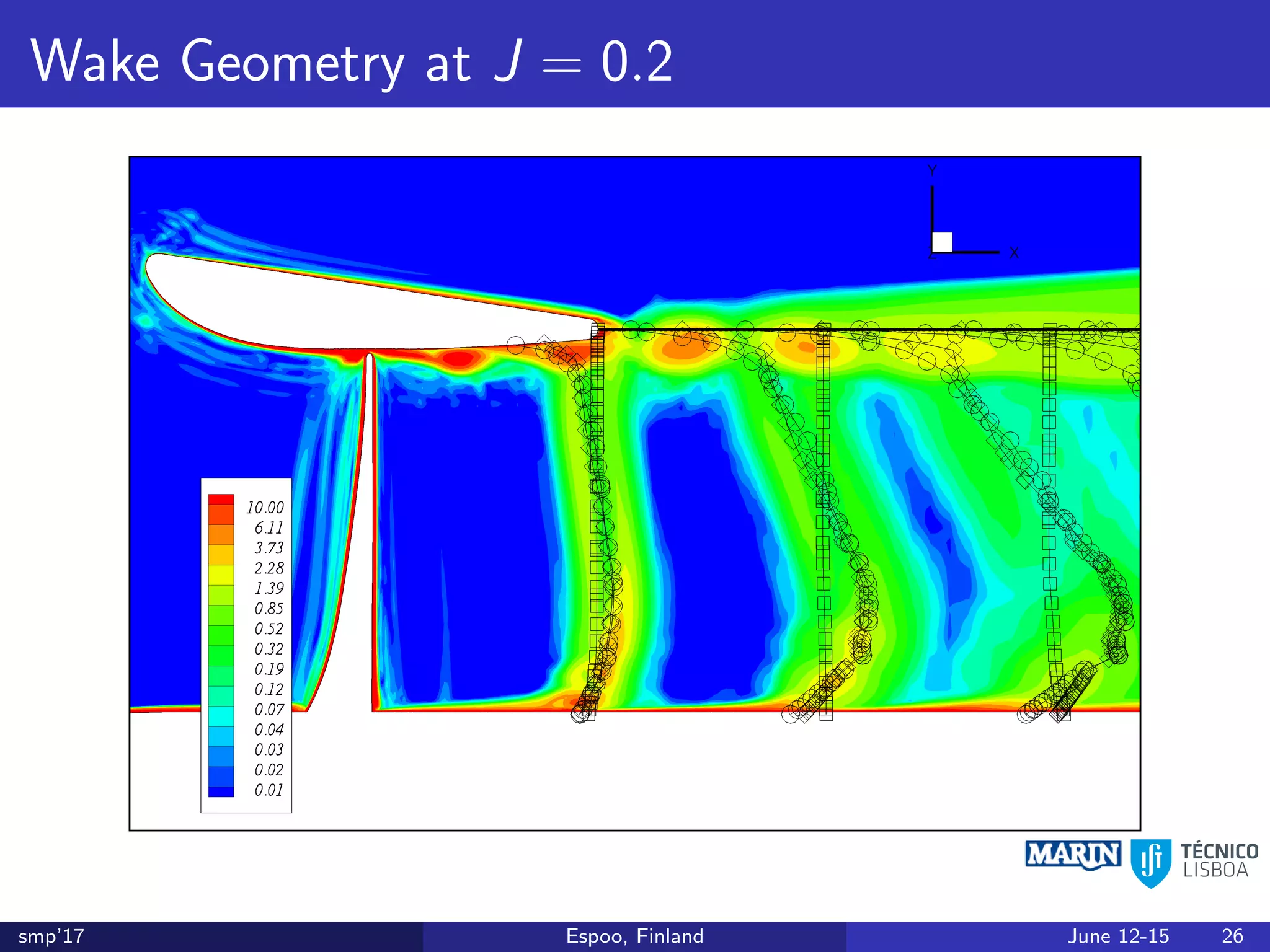
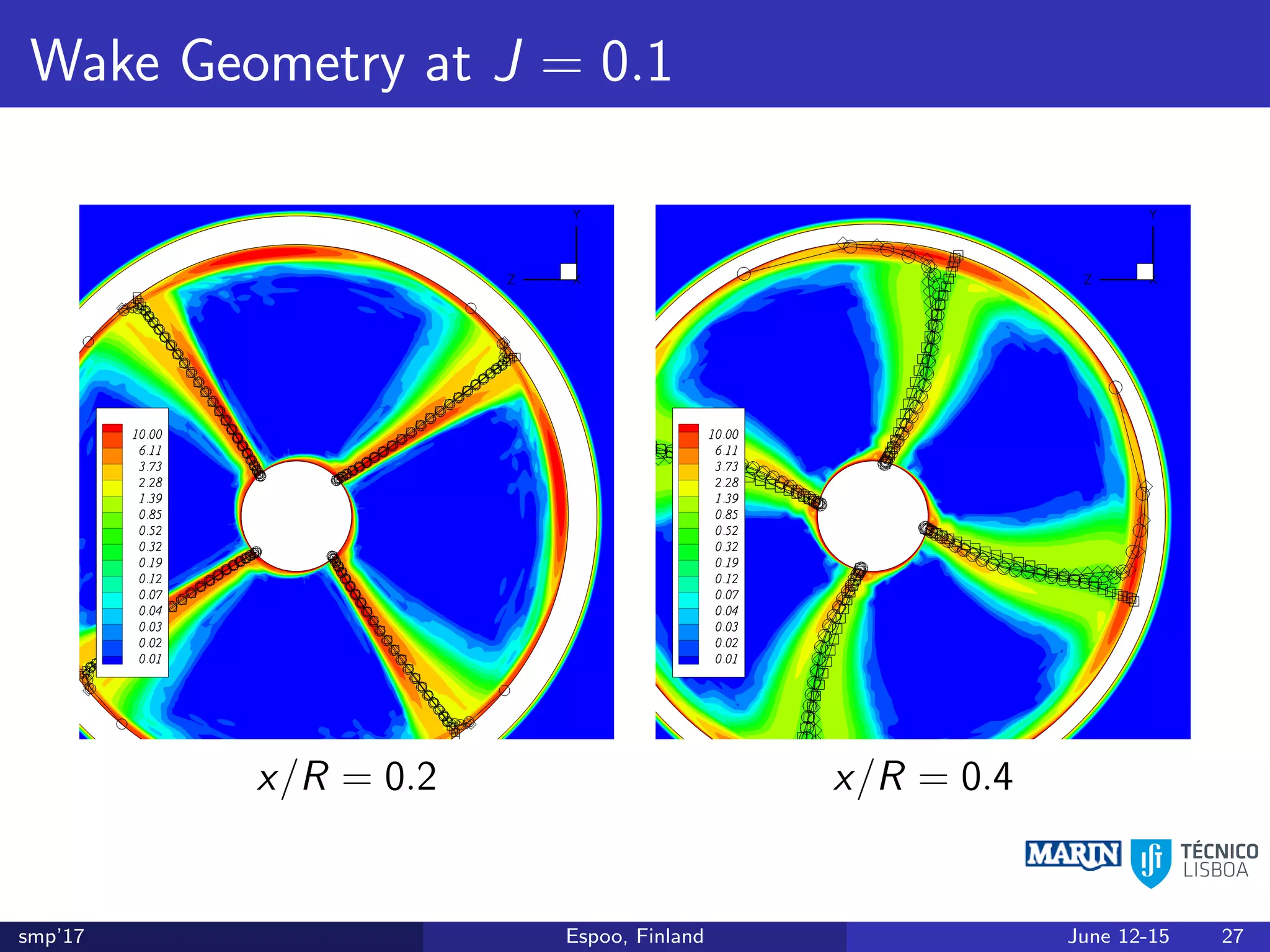
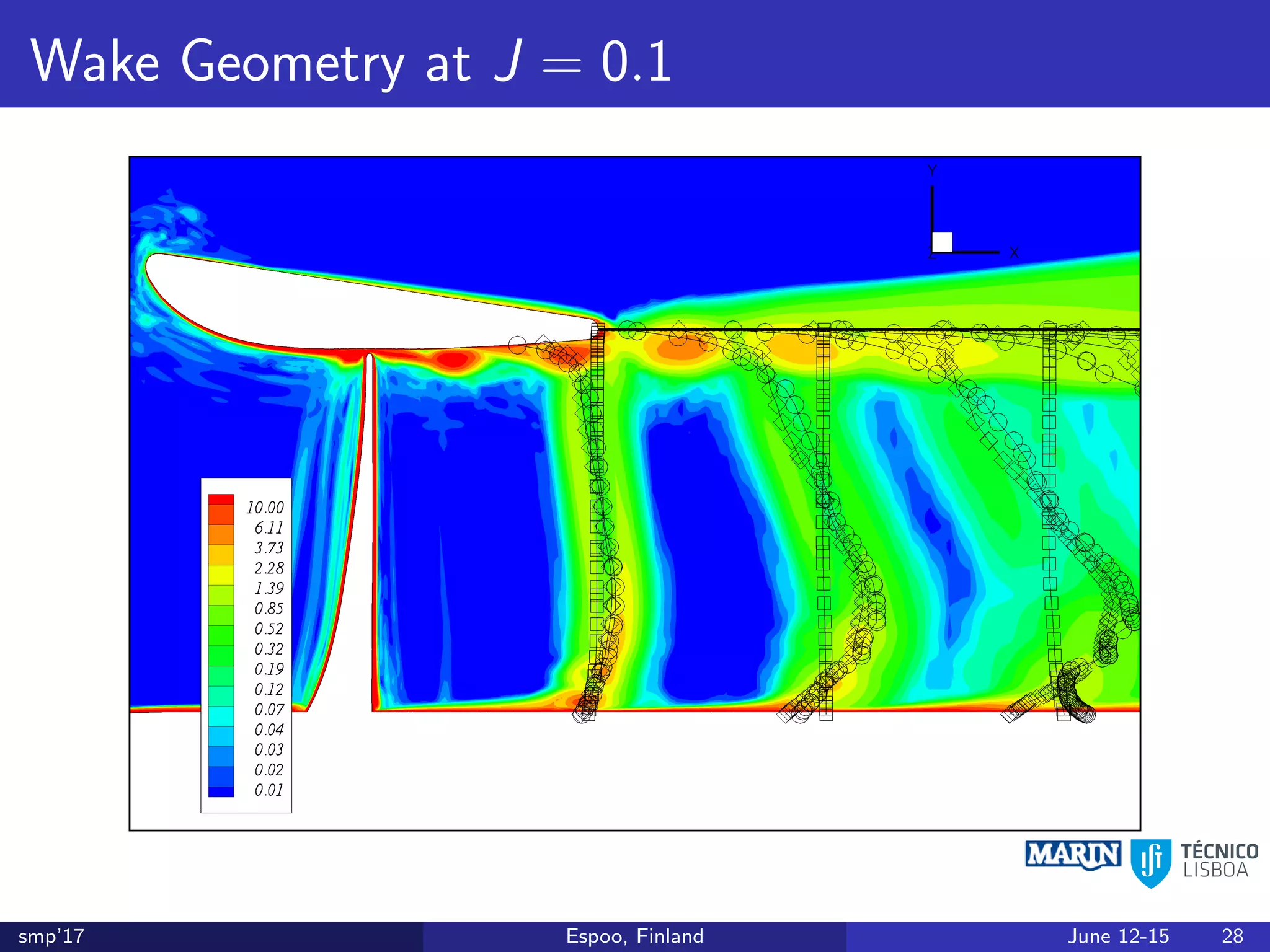
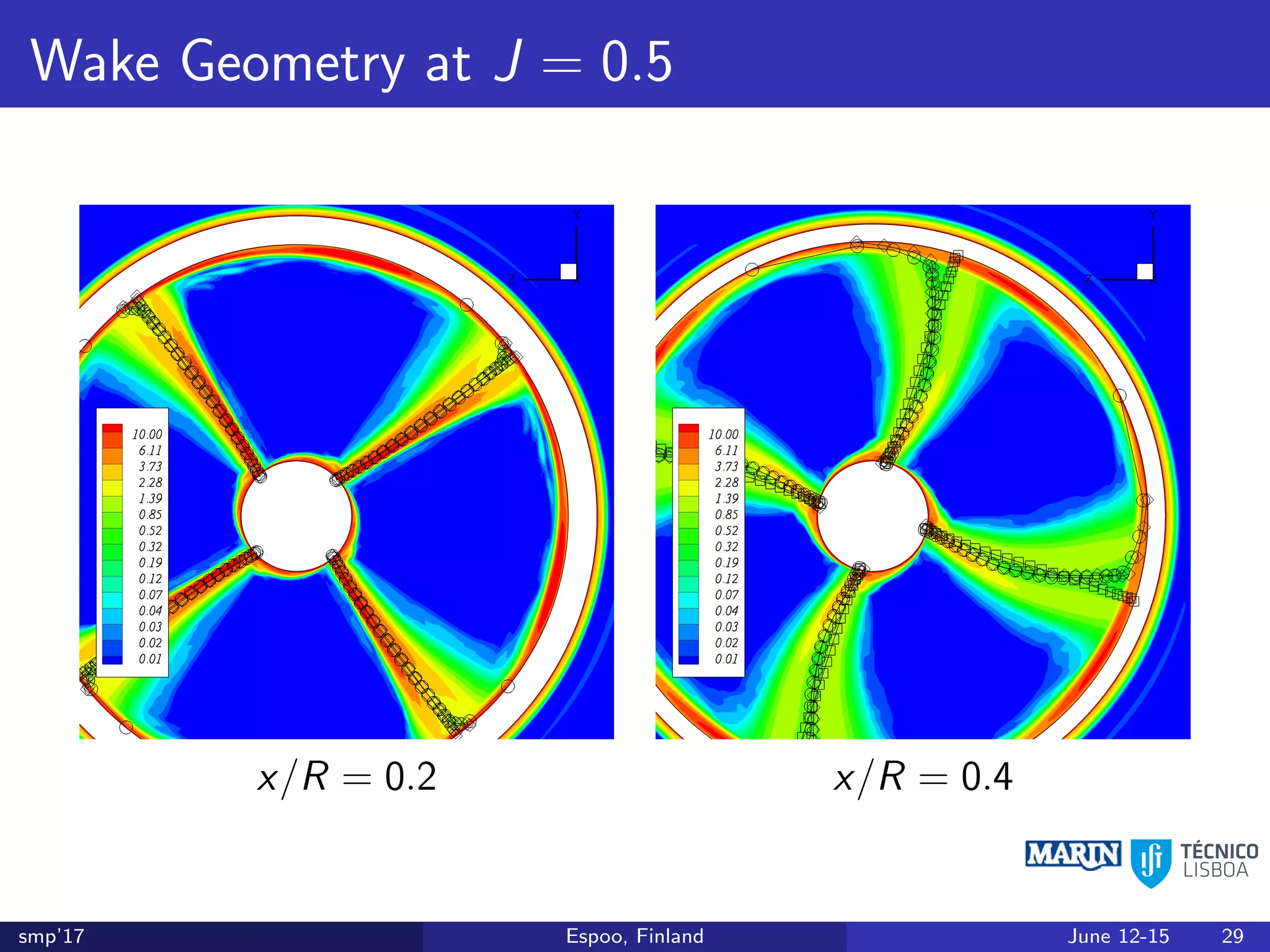
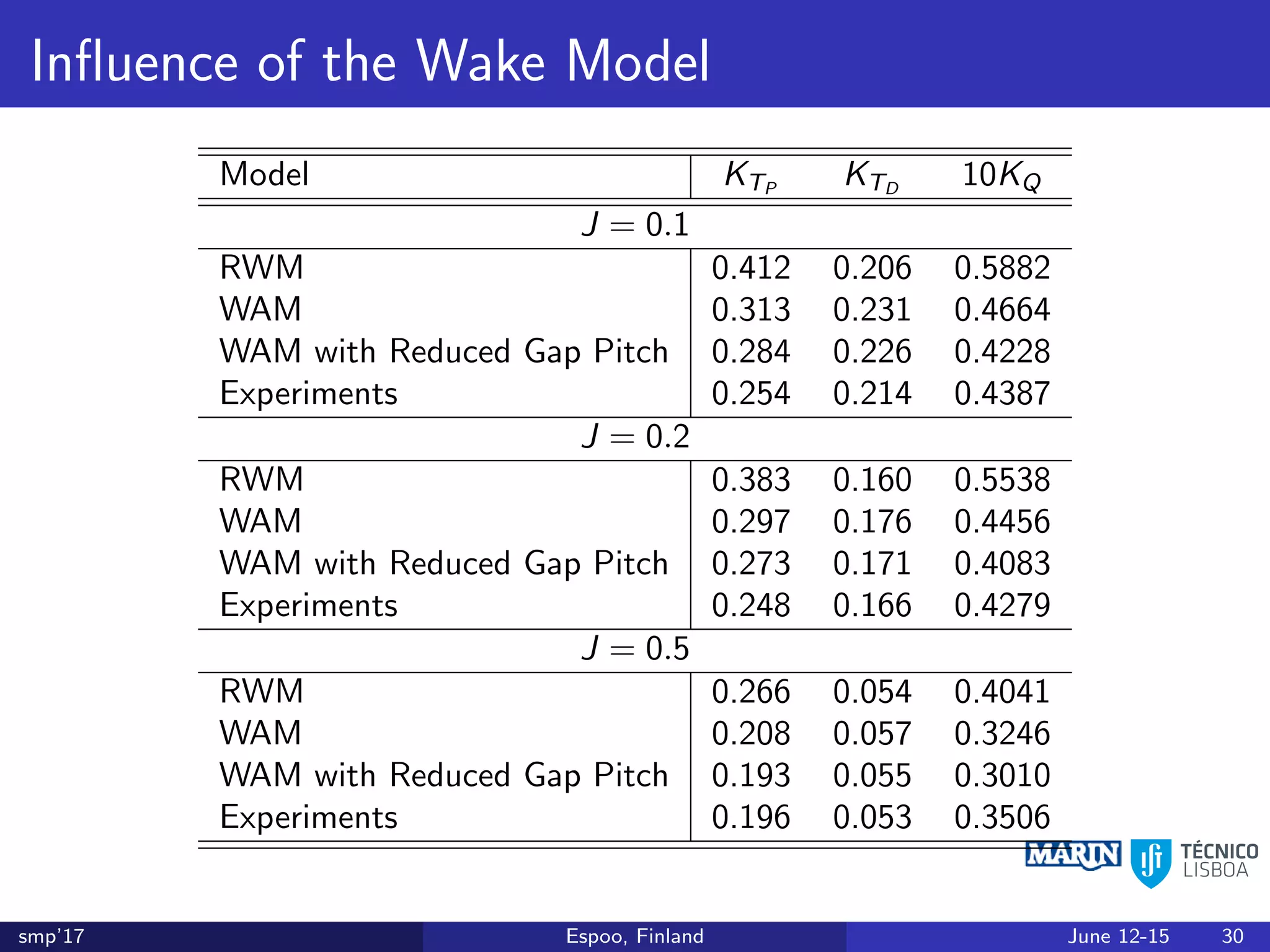
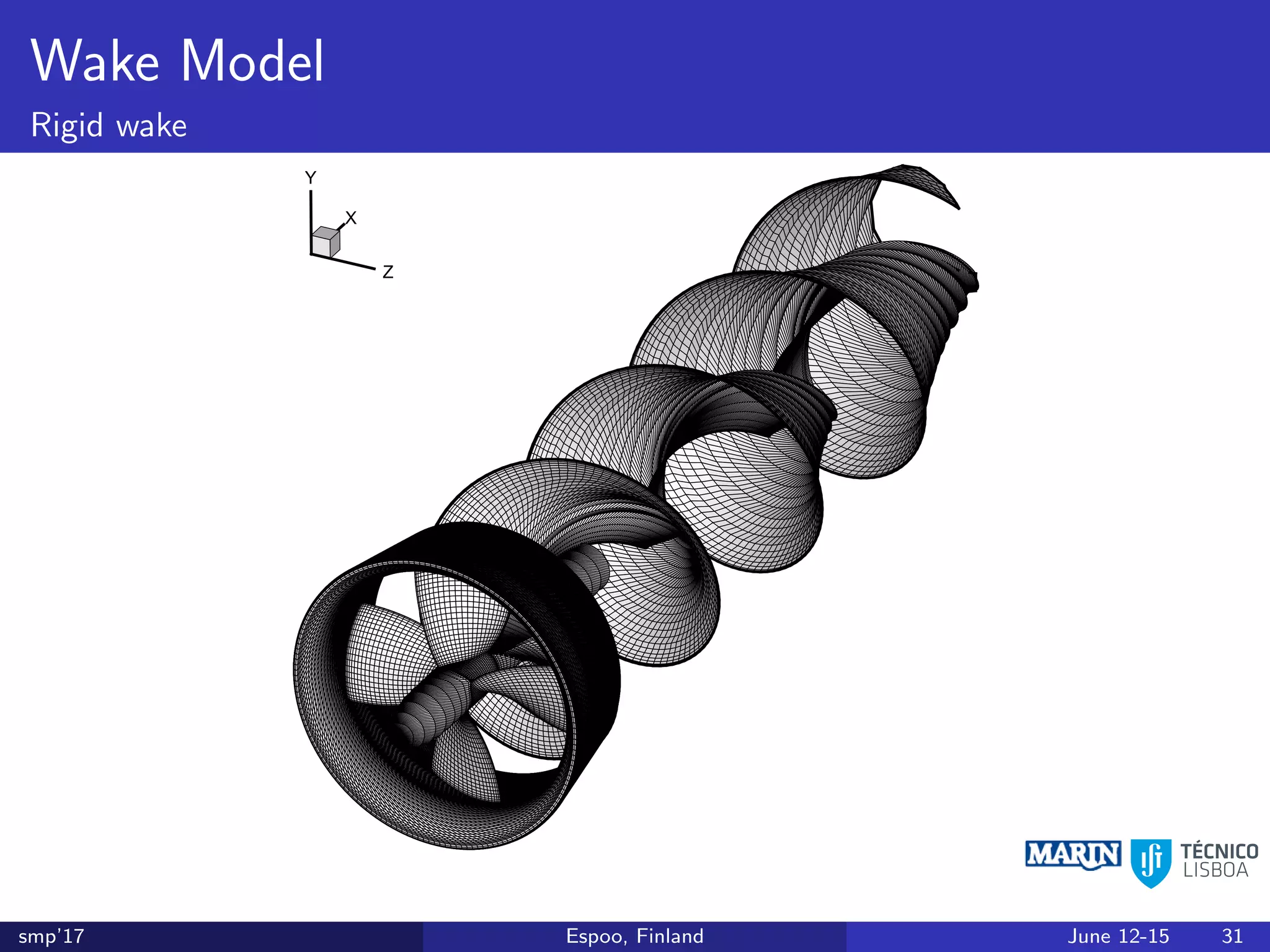
This document discusses the prediction of open-water performance for ducted propellers using a panel method. Panel methods provide a computationally efficient tool for analysis and design of marine propulsors. Application to ducted propellers involves additional modeling issues such as the complex interaction between propeller blades and duct surfaces. The document reviews previous work developing the panel method for ducted propellers, including models for the gap flow, wake alignment, duct boundary layers, and new Kutta conditions. It presents comparisons of panel method predictions to experimental and RANS results. The motivation is to improve performance predictions near bollard pull conditions through refinements to the numerical methods.

Embed presentation

Download as PDF, PPTX
Prediction of the Open-Water Performance of Ducted Propellers With a Panel Method J. Baltazar1, D. Rijpkema2, J.A.C. Falc˜ao de Campos1, J. Bosschers2 1Instituto Superior T´ecnico, Universidade de Lisboa, Portugal 2Maritime Research Institute Netherlands, Wageningen, the Netherlands smp’17 Espoo, Finland June 12-15 1
Introduction smp’17 Espoo, Finland June 12-15 2
Introduction Panel Methods (or BEM) still provide a most useful computational tool for analysis and design of marine propulsors smp’17 Espoo, Finland June 12-15 2
Introduction Panel Methods (or BEM) still provide a most useful computational tool for analysis and design of marine propulsors Main reasons for using Panel Methods: smp’17 Espoo, Finland June 12-15 2
Introduction Panel Methods (or BEM) still provide a most useful computational tool for analysis and design of marine propulsors Main reasons for using Panel Methods: Simplicity smp’17 Espoo, Finland June 12-15 2
Introduction Panel Methods (or BEM) still provide a most useful computational tool for analysis and design of marine propulsors Main reasons for using Panel Methods: Simplicity Computational efficiency smp’17 Espoo, Finland June 12-15 2
Introduction Panel Methods (or BEM) still provide a most useful computational tool for analysis and design of marine propulsors Main reasons for using Panel Methods: Simplicity Computational efficiency Direct relation to simpler design tools (lifting line and lifting surface) smp’17 Espoo, Finland June 12-15 2
Introduction Panel Methods (or BEM) still provide a most useful computational tool for analysis and design of marine propulsors Main reasons for using Panel Methods: Simplicity Computational efficiency Direct relation to simpler design tools (lifting line and lifting surface) Application to ducted propellers involves additional modelling issues: smp’17 Espoo, Finland June 12-15 2
Introduction Panel Methods (or BEM) still provide a most useful computational tool for analysis and design of marine propulsors Main reasons for using Panel Methods: Simplicity Computational efficiency Direct relation to simpler design tools (lifting line and lifting surface) Application to ducted propellers involves additional modelling issues: Complex interaction of propeller blades and duct surface – Gap flow – smp’17 Espoo, Finland June 12-15 2
Introduction Panel Methods (or BEM) still provide a most useful computational tool for analysis and design of marine propulsors Main reasons for using Panel Methods: Simplicity Computational efficiency Direct relation to simpler design tools (lifting line and lifting surface) Application to ducted propellers involves additional modelling issues: Complex interaction of propeller blades and duct surface – Gap flow – Thick duct trailing edges in practical applications – Kutta condition for round trailing edges – smp’17 Espoo, Finland June 12-15 2
Introduction Panel Methods (or BEM) still provide a most useful computational tool for analysis and design of marine propulsors Main reasons for using Panel Methods: Simplicity Computational efficiency Direct relation to simpler design tools (lifting line and lifting surface) Application to ducted propellers involves additional modelling issues: Complex interaction of propeller blades and duct surface – Gap flow – Thick duct trailing edges in practical applications – Kutta condition for round trailing edges – smp’17 Espoo, Finland June 12-15 2
Previous Work smp’17 Espoo, Finland June 12-15 3
Previous Work Rigid wake model, open and closed gap models (smp’09) smp’17 Espoo, Finland June 12-15 3
Previous Work Rigid wake model, open and closed gap models (smp’09) Wake alignment model for the blade wake, closed and transpiration velocity gap models, duct boundary layer correction (smp’11) smp’17 Espoo, Finland June 12-15 3
Previous Work Rigid wake model, open and closed gap models (smp’09) Wake alignment model for the blade wake, closed and transpiration velocity gap models, duct boundary layer correction (smp’11) Panel method results compared with RANS calculations and experimental open-water measurements (smp’13) smp’17 Espoo, Finland June 12-15 3
Previous Work Rigid wake model, open and closed gap models (smp’09) Wake alignment model for the blade wake, closed and transpiration velocity gap models, duct boundary layer correction (smp’11) Panel method results compared with RANS calculations and experimental open-water measurements (smp’13) New Kutta condition for thick duct trailing edges (smp’15) smp’17 Espoo, Finland June 12-15 3
Previous Work Rigid wake model, open and closed gap models (smp’09) Wake alignment model for the blade wake, closed and transpiration velocity gap models, duct boundary layer correction (smp’11) Panel method results compared with RANS calculations and experimental open-water measurements (smp’13) New Kutta condition for thick duct trailing edges (smp’15) RANS-BEM coupling for thick duct trailing edges (smp’15) smp’17 Espoo, Finland June 12-15 3
Duct Geometries smp’17 Espoo, Finland June 12-15 4
Open-Water Prediction Ka4-70 (P/D=1.0) inside Duct 19Am (shart duct t.e.) J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 Experiments: Re=ΩR/ν=1.23×10 6 KT 10KQ KTD P smp’17 Espoo, Finland June 12-15 5
Open-Water Prediction Ka4-70 (P/D=1.0) inside Duct 19Am (shart duct t.e.) J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 Experiments: Re=ΩR/ν=1.23×10 6 KT 10KQ KTD P J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 Experiments: Re=ΩR/ν=1.23×10 6 Rigid Wake Model KT 10KQ KTD P smp’17 Espoo, Finland June 12-15 5
Open-Water Prediction Ka4-70 (P/D=1.0) inside Duct 19Am (shart duct t.e.) J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 Experiments: Re=ΩR/ν=1.23×10 6 KT 10KQ KTD P J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 Experiments: Re=ΩR/ν=1.23×10 6 Rigid Wake Model KT 10KQ KTD P J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 Experiments: Re=ΩR/ν=1.23×10 6 Rigid Wake Model Wake Alignment Model (WAM) KT 10KQ KTD P smp’17 Espoo, Finland June 12-15 5
Open-Water Prediction Ka4-70 (P/D=1.0) inside Duct 19Am (shart duct t.e.) J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 Experiments: Re=ΩR/ν=1.23×10 6 KT 10KQ KTD P J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 Experiments: Re=ΩR/ν=1.23×10 6 Rigid Wake Model KT 10KQ KTD P J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 Experiments: Re=ΩR/ν=1.23×10 6 Rigid Wake Model Wake Alignment Model (WAM) KT 10KQ KTD P J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 Experiments: Re=ΩR/ν=1.23×10 6 Rigid Wake Model Wake Alignment Model (WAM) WAM with Duct Boundary Layer Correction KT 10KQ KTD P smp’17 Espoo, Finland June 12-15 5
New Wake Model Loading is critically dependent on the blade wake pitch, especially at tip RANS Panel Method smp’17 Espoo, Finland June 12-15 6
New Kutta Condition Location of the pressure-equality points as percentage of the duct length 0.40 0.45 0.50 0.55 0.60 Duct 19A 100.0% 99.9% 99.8% 99.5% 99.0% 97.0% 96.5% 98.0% smp’17 Espoo, Finland June 12-15 7
Open-Water Prediction Ka4-70 (P/D=1.0) inside Duct 19A J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 Experiments WAM, Closed Gap, Location at 97%, δ/R=4% WAM, Closed Gap, Location at 98%, δ/R=4% WAM, Closed Gap, Location at 99%, δ/R=4% KT 10KQ KT D P smp’17 Espoo, Finland June 12-15 8
Motivation smp’17 Espoo, Finland June 12-15 9
Motivation Panel Method: smp’17 Espoo, Finland June 12-15 9
Motivation Panel Method: Gap model (closed) smp’17 Espoo, Finland June 12-15 9
Motivation Panel Method: Gap model (closed) Wake alignment model smp’17 Espoo, Finland June 12-15 9
Motivation Panel Method: Gap model (closed) Wake alignment model Correction due to duct boundary layer smp’17 Espoo, Finland June 12-15 9
Motivation Panel Method: Gap model (closed) Wake alignment model Correction due to duct boundary layer New Kutta condition for thick duct t.e. smp’17 Espoo, Finland June 12-15 9
Motivation Panel Method: Gap model (closed) Wake alignment model Correction due to duct boundary layer New Kutta condition for thick duct t.e. Significant differences in the performance prediction close to bollard pull condition! smp’17 Espoo, Finland June 12-15 9
Motivation Panel Method: Gap model (closed) Wake alignment model Correction due to duct boundary layer New Kutta condition for thick duct t.e. Significant differences in the performance prediction close to bollard pull condition! Comparison between Panel Method and RANS calculations smp’17 Espoo, Finland June 12-15 9
Motivation Panel Method: Gap model (closed) Wake alignment model Correction due to duct boundary layer New Kutta condition for thick duct t.e. Significant differences in the performance prediction close to bollard pull condition! Comparison between Panel Method and RANS calculations smp’17 Espoo, Finland June 12-15 9
Numerical Methods smp’17 Espoo, Finland June 12-15 10
Numerical Methods Panel Code PROPAN smp’17 Espoo, Finland June 12-15 10
Numerical Methods Panel Code PROPAN IST in-house low-order potential-based panel method smp’17 Espoo, Finland June 12-15 10
Numerical Methods Panel Code PROPAN IST in-house low-order potential-based panel method Fredholm integral equation solved by the collocation method smp’17 Espoo, Finland June 12-15 10
Numerical Methods Panel Code PROPAN IST in-house low-order potential-based panel method Fredholm integral equation solved by the collocation method Structured surface grids smp’17 Espoo, Finland June 12-15 10
Numerical Methods Panel Code PROPAN IST in-house low-order potential-based panel method Fredholm integral equation solved by the collocation method Structured surface grids RANS Code ReFRESCO smp’17 Espoo, Finland June 12-15 10
Numerical Methods Panel Code PROPAN IST in-house low-order potential-based panel method Fredholm integral equation solved by the collocation method Structured surface grids RANS Code ReFRESCO Viscous flow CFD code (development led by MARIN) smp’17 Espoo, Finland June 12-15 10
Numerical Methods Panel Code PROPAN IST in-house low-order potential-based panel method Fredholm integral equation solved by the collocation method Structured surface grids RANS Code ReFRESCO Viscous flow CFD code (development led by MARIN) Finite volume discretisation smp’17 Espoo, Finland June 12-15 10
Numerical Methods Panel Code PROPAN IST in-house low-order potential-based panel method Fredholm integral equation solved by the collocation method Structured surface grids RANS Code ReFRESCO Viscous flow CFD code (development led by MARIN) Finite volume discretisation Turbulence model: k − ω SST 2-equation model by Menter (1994) smp’17 Espoo, Finland June 12-15 10
Numerical Methods Panel Code PROPAN IST in-house low-order potential-based panel method Fredholm integral equation solved by the collocation method Structured surface grids RANS Code ReFRESCO Viscous flow CFD code (development led by MARIN) Finite volume discretisation Turbulence model: k − ω SST 2-equation model by Menter (1994) No wal functions are used (y+ ∼ 1) smp’17 Espoo, Finland June 12-15 10
Grids PROPAN (left) and ReFRESCO (right) Blade: 50×26 27M Cells Duct: 190×160 smp’17 Espoo, Finland June 12-15 11
Blade Pressure Distribution at J = 0.5 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.5 0.0 0.5 1.0 RWM r/R=0.95 Cp=-1.0 smp’17 Espoo, Finland June 12-15 12
Blade Pressure Distribution at J = 0.5 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.5 0.0 0.5 1.0 RWM r/R=0.95 Cp=-1.0 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.5 0.0 0.5 1.0 RWM WAM r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -0.5 0.0 0.5 1.0 smp’17 Espoo, Finland June 12-15 12
Blade Pressure Distribution at J = 0.5 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.5 0.0 0.5 1.0 RWM r/R=0.95 Cp=-1.0 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.5 0.0 0.5 1.0 RWM WAM r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -0.5 0.0 0.5 1.0 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.5 0.0 0.5 1.0 ReFRESCO RWM WAM r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -0.5 0.0 0.5 1.0 smp’17 Espoo, Finland June 12-15 12
Duct Pressure Distribution at J = 0.5 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.2 -0.1 0.0 0.1 RWM θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 smp’17 Espoo, Finland June 12-15 13
Duct Pressure Distribution at J = 0.5 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.2 -0.1 0.0 0.1 RWM θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.2 -0.1 0.0 0.1 RWM WAM θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 smp’17 Espoo, Finland June 12-15 13
Duct Pressure Distribution at J = 0.5 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.2 -0.1 0.0 0.1 RWM θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.2 -0.1 0.0 0.1 RWM WAM θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.2 -0.1 0.0 0.1 ReFRESCO RWM WAM θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 smp’17 Espoo, Finland June 12-15 13
Blade Pressure Distribution at J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM r/R=0.95 Cp =-4.0 smp’17 Espoo, Finland June 12-15 14
Blade Pressure Distribution at J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM r/R=0.95 Cp =-4.0 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM WAM r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -2.0 -1.5 -1.0 -0.5 0.0 0.5 1.0 smp’17 Espoo, Finland June 12-15 14
Blade Pressure Distribution at J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM r/R=0.95 Cp =-4.0 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM WAM r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -2.0 -1.5 -1.0 -0.5 0.0 0.5 1.0 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 ReFRESCO RWM WAM r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -2.0 -1.5 -1.0 -0.5 0.0 0.5 1.0 smp’17 Espoo, Finland June 12-15 14
Duct Pressure Distribution at J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM θ=0º smp’17 Espoo, Finland June 12-15 15
Duct Pressure Distribution at J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM θ=0º s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM WAM θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 smp’17 Espoo, Finland June 12-15 15
Duct Pressure Distribution at J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM θ=0º s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM WAM θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 ReFRESCO RWM WAM θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 smp’17 Espoo, Finland June 12-15 15
Reduced Gap Pitch (P/D=0.9) X Y Z Blade Blade Wake Gap Strip smp’17 Espoo, Finland June 12-15 16
Reduced Gap Pitch (P/D=0.9) X Y Z Blade Blade Wake Gap Strip X Y Z Blade Blade Wake Gap Strip smp’17 Espoo, Finland June 12-15 16
Tip Leakage Flow smp’17 Espoo, Finland June 12-15 17
Pressure Distribution at J = 0.5 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.5 0.0 0.5 1.0 ReFRESCO RWM WAM WAM with Reduced Gap Pitch r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -0.5 0.0 0.5 1.0 smp’17 Espoo, Finland June 12-15 18
Pressure Distribution at J = 0.5 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.2 -0.1 0.0 0.1 ReFRESCO RWM WAM WAM with Reduced Gap Pitch θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 smp’17 Espoo, Finland June 12-15 19
Blade Pressure Distribution at J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM r/R=0.95 Cp =-4.0 smp’17 Espoo, Finland June 12-15 20
Blade Pressure Distribution at J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM r/R=0.95 Cp =-4.0 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM WAM r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -2.0 -1.5 -1.0 -0.5 0.0 0.5 1.0 smp’17 Espoo, Finland June 12-15 20
Blade Pressure Distribution at J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM r/R=0.95 Cp =-4.0 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM WAM r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -2.0 -1.5 -1.0 -0.5 0.0 0.5 1.0 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM WAM WAM with Reduced Gap Pitch r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -2.0 -1.5 -1.0 -0.5 0.0 0.5 1.0 smp’17 Espoo, Finland June 12-15 20
Blade Pressure Distribution at J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM r/R=0.95 Cp =-4.0 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM WAM r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -2.0 -1.5 -1.0 -0.5 0.0 0.5 1.0 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM WAM WAM with Reduced Gap Pitch r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -2.0 -1.5 -1.0 -0.5 0.0 0.5 1.0 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 ReFRESCO RWM WAM WAM with Reduced Gap Pitch r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -2.0 -1.5 -1.0 -0.5 0.0 0.5 1.0 smp’17 Espoo, Finland June 12-15 20
Duct Pressure Distribution at J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM θ=0º smp’17 Espoo, Finland June 12-15 21
Duct Pressure Distribution at J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM θ=0º s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM WAM θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 smp’17 Espoo, Finland June 12-15 21
Duct Pressure Distribution at J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM θ=0º s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM WAM θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM WAM WAM with Reduced Gap Pitch θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 smp’17 Espoo, Finland June 12-15 21
Duct Pressure Distribution at J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM θ=0º s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM WAM θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM WAM WAM with Reduced Gap Pitch θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 ReFRESCO RWM WAM WAM with Reduced Gap Pitch θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 smp’17 Espoo, Finland June 12-15 21
Open-Water Prediction Ka4-70 (P/D=1.0) inside Duct 19A J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 Experiments KT 10KQ KT D P smp’17 Espoo, Finland June 12-15 22
Open-Water Prediction Ka4-70 (P/D=1.0) inside Duct 19A J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 Experiments KT 10KQ KT D P J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 Experiments ReFRESCO KT 10KQ KT D P smp’17 Espoo, Finland June 12-15 22
Open-Water Prediction Ka4-70 (P/D=1.0) inside Duct 19A J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 Experiments KT 10KQ KT D P J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 Experiments ReFRESCO KT 10KQ KT D P J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 Experiments ReFRESCO WAM KT 10KQ KT D P smp’17 Espoo, Finland June 12-15 22
Open-Water Prediction Ka4-70 (P/D=1.0) inside Duct 19A J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 Experiments KT 10KQ KT D P J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 Experiments ReFRESCO KT 10KQ KT D P J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 Experiments ReFRESCO WAM KT 10KQ KT D P J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 Experiments ReFRESCO WAM WAM with Reduced Gap Pitch KT 10KQ KT D P smp’17 Espoo, Finland June 12-15 22
Conclusions smp’17 Espoo, Finland June 12-15 23
Conclusions Prediction of the ducted propeller loading is critically dependent on the blade wake pitch, especially at tip! smp’17 Espoo, Finland June 12-15 23
Conclusions Prediction of the ducted propeller loading is critically dependent on the blade wake pitch, especially at tip! The flow in the tip region is particularly important near bollard pull smp’17 Espoo, Finland June 12-15 23
Conclusions Prediction of the ducted propeller loading is critically dependent on the blade wake pitch, especially at tip! The flow in the tip region is particularly important near bollard pull Future work: smp’17 Espoo, Finland June 12-15 23
Conclusions Prediction of the ducted propeller loading is critically dependent on the blade wake pitch, especially at tip! The flow in the tip region is particularly important near bollard pull Future work: Include reduction of the gap strip in wake alignment model smp’17 Espoo, Finland June 12-15 23
Conclusions Prediction of the ducted propeller loading is critically dependent on the blade wake pitch, especially at tip! The flow in the tip region is particularly important near bollard pull Future work: Include reduction of the gap strip in wake alignment model Robustness issues are expected smp’17 Espoo, Finland June 12-15 23
Pressure Distribution at J = 0.2 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 ReFRESCO RWM WAM WAM with Reduced Gap Pitch r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -2.0 -1.5 -1.0 -0.5 0.0 0.5 1.0 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 ReFRESCO RWM WAM WAM with Reduced Gap Pitch θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 smp’17 Espoo, Finland June 12-15 24
Wake Geometry at J = 0.2 x/R = 0.2 x/R = 0.4 smp’17 Espoo, Finland June 12-15 25
Wake Geometry at J = 0.2 smp’17 Espoo, Finland June 12-15 26
Wake Geometry at J = 0.1 x/R = 0.2 x/R = 0.4 smp’17 Espoo, Finland June 12-15 27
Wake Geometry at J = 0.1 smp’17 Espoo, Finland June 12-15 28
Wake Geometry at J = 0.5 x/R = 0.2 x/R = 0.4 smp’17 Espoo, Finland June 12-15 29
Influence of the Wake Model Model KTP KTD 10KQ J = 0.1 RWM 0.412 0.206 0.5882 WAM 0.313 0.231 0.4664 WAM with Reduced Gap Pitch 0.284 0.226 0.4228 Experiments 0.254 0.214 0.4387 J = 0.2 RWM 0.383 0.160 0.5538 WAM 0.297 0.176 0.4456 WAM with Reduced Gap Pitch 0.273 0.171 0.4083 Experiments 0.248 0.166 0.4279 J = 0.5 RWM 0.266 0.054 0.4041 WAM 0.208 0.057 0.3246 WAM with Reduced Gap Pitch 0.193 0.055 0.3010 Experiments 0.196 0.053 0.3506 smp’17 Espoo, Finland June 12-15 30
Wake Model Rigid wake X Y Z smp’17 Espoo, Finland June 12-15 31
Wake Model Aligned wake with b.l. correction X Y Z smp’17 Espoo, Finland June 12-15 32

More Related Content

PDF
On the Use of the \gamma-Re_\theta Transition Model for the Prediction of the...
byJoão Baltazar
 
PDF
PROPAN - Propeller Panel Code
byJoão Baltazar
 
PDF
Hydrodynamic Analysis of a Horizontal Axis Marine Current Turbine with a Boun...
byJoão Baltazar
 
PDF
Potential Flow Modelling of Ducted Propellers with Blunt Trailing Edge Duct U...
byJoão Baltazar
 
PDF
Open-Water Thrust and Torque Predictions of a Ducted Propeller System With a ...
byJoão Baltazar
 
PDF
Numerical Modelling of the Potential Flow Around Ducted Propellers
byJoão Baltazar
 
PDF
On the Modelling of the Flow in Ducted Propellers
byJoão Baltazar
 
PDF
Unsteady Analysis of a Horizontal Axis Marine Current Turbine in Yawed Inflow...
byJoão Baltazar
 
On the Use of the \gamma-Re_\theta Transition Model for the Prediction of the...
byJoão Baltazar
 
PROPAN - Propeller Panel Code
byJoão Baltazar
 
Hydrodynamic Analysis of a Horizontal Axis Marine Current Turbine with a Boun...
byJoão Baltazar
 
Potential Flow Modelling of Ducted Propellers with Blunt Trailing Edge Duct U...
byJoão Baltazar
 
Open-Water Thrust and Torque Predictions of a Ducted Propeller System With a ...
byJoão Baltazar
 
Numerical Modelling of the Potential Flow Around Ducted Propellers
byJoão Baltazar
 
On the Modelling of the Flow in Ducted Propellers
byJoão Baltazar
 
Unsteady Analysis of a Horizontal Axis Marine Current Turbine in Yawed Inflow...
byJoão Baltazar
 

Similar to Prediction of the Open-Water Performance of Ducted Propellers With a Panel Method

PDF
Modelling of Laminar-to-Turbulent Flow Transition on a Marine Propeller Using...
byJoão Baltazar
 
PDF
Prediction of Sheet Cavitation on Marine Current Turbines With a Boundary Ele...
byJoão Baltazar
 
PDF
Leading-Edge Vortex Flow Modelling Around Delta Wings Using a Boundary Elemen...
byJoão Baltazar
 
PDF
Hydrodynamic Design and Analysis of Horizontal Axis Marine Current Turbines W...
byJoão Baltazar
 
PDF
Qblade an open source tool for design and simulation
byPhuong Dx
 
PDF
Analysis of the Blade Boundary-Layer Flow of a Marine Propeller with RANSE
byJoão Baltazar
 
PDF
A Numerical Study on the Iterative Techniques to Solve Partial Cavitation on ...
byJoão Baltazar
 
PDF
A Comparison of Panel Method and RANS Calculations for a Ducted Propeller Sys...
byJoão Baltazar
 
PDF
Prediction of Unsteady Sheet Cavitation on Marine Current Turbines With a Bou...
byJoão Baltazar
 
PDF
Recent Developments in Computational Methods for the Analysis of Ducted Prope...
byJoão Baltazar
 
PDF
Recent Developments in Computational Methods for the Analysis of Ducted Prope...
byJoão Baltazar
 
PDF
A potential panel method for prediction of midchord face and back cavitation ...
byPhuong Dx
 
PDF
Numerical Studies for Verification and Validation of Open-Water Propeller RAN...
byJoão Baltazar
 
PDF
mets2016_poster_SaleAliseda
byDanny Sale
 
Modelling of Laminar-to-Turbulent Flow Transition on a Marine Propeller Using...
byJoão Baltazar
 
Prediction of Sheet Cavitation on Marine Current Turbines With a Boundary Ele...
byJoão Baltazar
 
Leading-Edge Vortex Flow Modelling Around Delta Wings Using a Boundary Elemen...
byJoão Baltazar
 
Hydrodynamic Design and Analysis of Horizontal Axis Marine Current Turbines W...
byJoão Baltazar
 
Qblade an open source tool for design and simulation
byPhuong Dx
 
Analysis of the Blade Boundary-Layer Flow of a Marine Propeller with RANSE
byJoão Baltazar
 
A Numerical Study on the Iterative Techniques to Solve Partial Cavitation on ...
byJoão Baltazar
 
A Comparison of Panel Method and RANS Calculations for a Ducted Propeller Sys...
byJoão Baltazar
 
Prediction of Unsteady Sheet Cavitation on Marine Current Turbines With a Bou...
byJoão Baltazar
 
Recent Developments in Computational Methods for the Analysis of Ducted Prope...
byJoão Baltazar
 
Recent Developments in Computational Methods for the Analysis of Ducted Prope...
byJoão Baltazar
 
A potential panel method for prediction of midchord face and back cavitation ...
byPhuong Dx
 
Numerical Studies for Verification and Validation of Open-Water Propeller RAN...
byJoão Baltazar
 
mets2016_poster_SaleAliseda
byDanny Sale
 

More from João Baltazar

PDF
Prediction of the Propeller Performance at Different Reynolds Number Regimes ...
byJoão Baltazar
 
PDF
An Iteratively Coupled Solution Method for Partial and Super-Cavitation Predi...
byJoão Baltazar
 
PDF
Design of a Horizontal Axis Marine Current Turbine with Dedicated Hydrofoil S...
byJoão Baltazar
 
PPT
Unsteady Potential Flow Calculations of Marine Propellers Using BEM
byJoão Baltazar
 
PDF
A Numerical Study on the Application of BEM to Steady Cavitating Potential Fl...
byJoão Baltazar
 
PDF
A Study on the Modeling of Marine Propeller Tip Flows Using BEM
byJoão Baltazar
 
PDF
A Comparison of Panel Method and RANS Calculations for a Horizontal Axis Mari...
byJoão Baltazar
 
PDF
A Study on the Accuracy of Low and Higher Order BEM in Three Dimensional Pote...
byJoão Baltazar
 
PDF
Potential Flow Modelling of Ducted Propellers With a Panel Method
byJoão Baltazar
 
PDF
A Surface Grid Generation Technique for Practical Applications of Boundary El...
byJoão Baltazar
 
PDF
Propeller Performance Prediction in an Artificially Generated Wake Field Usin...
byJoão Baltazar
 
PDF
A Boundary Element Method for the Unsteady Hydrodynamic Analysis of Marine Cu...
byJoão Baltazar
 
PDF
Unsteady Potential Flow Calculations on a Horizontal Axis Marine Current Turb...
byJoão Baltazar
 
PDF
Estudo Experimental do Balanço Transversal
byJoão Baltazar
 
Prediction of the Propeller Performance at Different Reynolds Number Regimes ...
byJoão Baltazar
 
An Iteratively Coupled Solution Method for Partial and Super-Cavitation Predi...
byJoão Baltazar
 
Design of a Horizontal Axis Marine Current Turbine with Dedicated Hydrofoil S...
byJoão Baltazar
 
Unsteady Potential Flow Calculations of Marine Propellers Using BEM
byJoão Baltazar
 
A Numerical Study on the Application of BEM to Steady Cavitating Potential Fl...
byJoão Baltazar
 
A Study on the Modeling of Marine Propeller Tip Flows Using BEM
byJoão Baltazar
 
A Comparison of Panel Method and RANS Calculations for a Horizontal Axis Mari...
byJoão Baltazar
 
A Study on the Accuracy of Low and Higher Order BEM in Three Dimensional Pote...
byJoão Baltazar
 
Potential Flow Modelling of Ducted Propellers With a Panel Method
byJoão Baltazar
 
A Surface Grid Generation Technique for Practical Applications of Boundary El...
byJoão Baltazar
 
Propeller Performance Prediction in an Artificially Generated Wake Field Usin...
byJoão Baltazar
 
A Boundary Element Method for the Unsteady Hydrodynamic Analysis of Marine Cu...
byJoão Baltazar
 
Unsteady Potential Flow Calculations on a Horizontal Axis Marine Current Turb...
byJoão Baltazar
 
Estudo Experimental do Balanço Transversal
byJoão Baltazar
 

Recently uploaded

PPTX
ISO 14224 Compliance & CMMS Software — A Comprehensive Guide for Reliable Mai...
byMaintWiz Technologies Private Limited
 
PDF
Structural Conservation Appraisal of Indian Monuments Preserving India’s Arch...
byAman Kumar Singh
 
PPTX
Engineering Economics CHAPTER 4.pptx - R
byMisgnaArefe
 
PPTX
The Complete Guide to Energy Audits_ Unlocking Savings, Sustainability, and P...
bygreentechnexus2024
 
PPTX
22PEOIT4C Session 4 Breath First Search & Depth First Search.pptx
bymailmegokilavani
 
PPTX
22PEOIT4C Session 9 Local search in continuous space.pptx
bymailmegokilavani
 
PPTX
Power point presentation on introduction of software engineering
bys6050748
 
PPTX
A7383 3D Printing UNIT-III : 3D printing techniques
byVishnuVardhan909561
 
PPTX
Introduction Blockchains and Smart Contracts
bybobinson
 
PPTX
How to Create an Effective Monthly Preventive Maintenance Plan
byMaintWiz Technologies Private Limited
 
PDF
PROPEX-RAG: Prompt-Driven GraphRAG for Multi-Hop QA
byapurvakarne
 
PPTX
Cloud vs On-Premises CMMS — Which Maintenance Platform Is Better for Your Plant?
byMaintWiz Technologies Private Limited
 
PPTX
Optimizing Operations: Key Elements of a Successful Plant Maintenance Plan — ...
byMaintWiz Technologies Private Limited
 
PDF
TechSprint: Innovate for Impact Hackathon
byDeepakkumarSingh415123
 
PPTX
Network Security v1.0 - Module 2.pptx
byssuserb1479b
 
PPTX
MODULE 1-UNIT_1.pptx MODULE 1-UNIT_1.pptx MODULE 1-UNIT_1.pptx
bypavanscholar123
 
PDF
Nostr : A protocol for freedom of speech
byEmre YILMAZ
 
PPTX
1_Sources of security threats, Motives, Target.pptx
bydolly475229
 
PDF
22PEOIT4C Artificial Intelligence Syllab
bymailmegokilavani
 
PPTX
2_Consequence of threats, E-mail threats, Web.pptx
bydolly475229
 
ISO 14224 Compliance & CMMS Software — A Comprehensive Guide for Reliable Mai...
byMaintWiz Technologies Private Limited
 
Structural Conservation Appraisal of Indian Monuments Preserving India’s Arch...
byAman Kumar Singh
 
Engineering Economics CHAPTER 4.pptx - R
byMisgnaArefe
 
The Complete Guide to Energy Audits_ Unlocking Savings, Sustainability, and P...
bygreentechnexus2024
 
22PEOIT4C Session 4 Breath First Search & Depth First Search.pptx
bymailmegokilavani
 
22PEOIT4C Session 9 Local search in continuous space.pptx
bymailmegokilavani
 
Power point presentation on introduction of software engineering
bys6050748
 
A7383 3D Printing UNIT-III : 3D printing techniques
byVishnuVardhan909561
 
Introduction Blockchains and Smart Contracts
bybobinson
 
How to Create an Effective Monthly Preventive Maintenance Plan
byMaintWiz Technologies Private Limited
 
PROPEX-RAG: Prompt-Driven GraphRAG for Multi-Hop QA
byapurvakarne
 
Cloud vs On-Premises CMMS — Which Maintenance Platform Is Better for Your Plant?
byMaintWiz Technologies Private Limited
 
Optimizing Operations: Key Elements of a Successful Plant Maintenance Plan — ...
byMaintWiz Technologies Private Limited
 
TechSprint: Innovate for Impact Hackathon
byDeepakkumarSingh415123
 
Network Security v1.0 - Module 2.pptx
byssuserb1479b
 
MODULE 1-UNIT_1.pptx MODULE 1-UNIT_1.pptx MODULE 1-UNIT_1.pptx
bypavanscholar123
 
Nostr : A protocol for freedom of speech
byEmre YILMAZ
 
1_Sources of security threats, Motives, Target.pptx
bydolly475229
 
22PEOIT4C Artificial Intelligence Syllab
bymailmegokilavani
 
2_Consequence of threats, E-mail threats, Web.pptx
bydolly475229
 

Prediction of the Open-Water Performance of Ducted Propellers With a Panel Method

  • 1.
    Prediction of theOpen-Water Performance of Ducted Propellers With a Panel Method J. Baltazar1, D. Rijpkema2, J.A.C. Falc˜ao de Campos1, J. Bosschers2 1Instituto Superior T´ecnico, Universidade de Lisboa, Portugal 2Maritime Research Institute Netherlands, Wageningen, the Netherlands smp’17 Espoo, Finland June 12-15 1
  • 2.
  • 3.
    Introduction Panel Methods (orBEM) still provide a most useful computational tool for analysis and design of marine propulsors smp’17 Espoo, Finland June 12-15 2
  • 4.
    Introduction Panel Methods (orBEM) still provide a most useful computational tool for analysis and design of marine propulsors Main reasons for using Panel Methods: smp’17 Espoo, Finland June 12-15 2
  • 5.
    Introduction Panel Methods (orBEM) still provide a most useful computational tool for analysis and design of marine propulsors Main reasons for using Panel Methods: Simplicity smp’17 Espoo, Finland June 12-15 2
  • 6.
    Introduction Panel Methods (orBEM) still provide a most useful computational tool for analysis and design of marine propulsors Main reasons for using Panel Methods: Simplicity Computational efficiency smp’17 Espoo, Finland June 12-15 2
  • 7.
    Introduction Panel Methods (orBEM) still provide a most useful computational tool for analysis and design of marine propulsors Main reasons for using Panel Methods: Simplicity Computational efficiency Direct relation to simpler design tools (lifting line and lifting surface) smp’17 Espoo, Finland June 12-15 2
  • 8.
    Introduction Panel Methods (orBEM) still provide a most useful computational tool for analysis and design of marine propulsors Main reasons for using Panel Methods: Simplicity Computational efficiency Direct relation to simpler design tools (lifting line and lifting surface) Application to ducted propellers involves additional modelling issues: smp’17 Espoo, Finland June 12-15 2
  • 9.
    Introduction Panel Methods (orBEM) still provide a most useful computational tool for analysis and design of marine propulsors Main reasons for using Panel Methods: Simplicity Computational efficiency Direct relation to simpler design tools (lifting line and lifting surface) Application to ducted propellers involves additional modelling issues: Complex interaction of propeller blades and duct surface – Gap flow – smp’17 Espoo, Finland June 12-15 2
  • 10.
    Introduction Panel Methods (orBEM) still provide a most useful computational tool for analysis and design of marine propulsors Main reasons for using Panel Methods: Simplicity Computational efficiency Direct relation to simpler design tools (lifting line and lifting surface) Application to ducted propellers involves additional modelling issues: Complex interaction of propeller blades and duct surface – Gap flow – Thick duct trailing edges in practical applications – Kutta condition for round trailing edges – smp’17 Espoo, Finland June 12-15 2
  • 11.
    Introduction Panel Methods (orBEM) still provide a most useful computational tool for analysis and design of marine propulsors Main reasons for using Panel Methods: Simplicity Computational efficiency Direct relation to simpler design tools (lifting line and lifting surface) Application to ducted propellers involves additional modelling issues: Complex interaction of propeller blades and duct surface – Gap flow – Thick duct trailing edges in practical applications – Kutta condition for round trailing edges – smp’17 Espoo, Finland June 12-15 2
  • 12.
    Previous Work smp’17 Espoo,Finland June 12-15 3
  • 13.
    Previous Work Rigid wakemodel, open and closed gap models (smp’09) smp’17 Espoo, Finland June 12-15 3
  • 14.
    Previous Work Rigid wakemodel, open and closed gap models (smp’09) Wake alignment model for the blade wake, closed and transpiration velocity gap models, duct boundary layer correction (smp’11) smp’17 Espoo, Finland June 12-15 3
  • 15.
    Previous Work Rigid wakemodel, open and closed gap models (smp’09) Wake alignment model for the blade wake, closed and transpiration velocity gap models, duct boundary layer correction (smp’11) Panel method results compared with RANS calculations and experimental open-water measurements (smp’13) smp’17 Espoo, Finland June 12-15 3
  • 16.
    Previous Work Rigid wakemodel, open and closed gap models (smp’09) Wake alignment model for the blade wake, closed and transpiration velocity gap models, duct boundary layer correction (smp’11) Panel method results compared with RANS calculations and experimental open-water measurements (smp’13) New Kutta condition for thick duct trailing edges (smp’15) smp’17 Espoo, Finland June 12-15 3
  • 17.
    Previous Work Rigid wakemodel, open and closed gap models (smp’09) Wake alignment model for the blade wake, closed and transpiration velocity gap models, duct boundary layer correction (smp’11) Panel method results compared with RANS calculations and experimental open-water measurements (smp’13) New Kutta condition for thick duct trailing edges (smp’15) RANS-BEM coupling for thick duct trailing edges (smp’15) smp’17 Espoo, Finland June 12-15 3
  • 18.
    Duct Geometries smp’17 Espoo,Finland June 12-15 4
  • 19.
    Open-Water Prediction Ka4-70 (P/D=1.0)inside Duct 19Am (shart duct t.e.) J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 Experiments: Re=ΩR/ν=1.23×10 6 KT 10KQ KTD P smp’17 Espoo, Finland June 12-15 5
  • 20.
    Open-Water Prediction Ka4-70 (P/D=1.0)inside Duct 19Am (shart duct t.e.) J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 Experiments: Re=ΩR/ν=1.23×10 6 KT 10KQ KTD P J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 Experiments: Re=ΩR/ν=1.23×10 6 Rigid Wake Model KT 10KQ KTD P smp’17 Espoo, Finland June 12-15 5
  • 21.
    Open-Water Prediction Ka4-70 (P/D=1.0)inside Duct 19Am (shart duct t.e.) J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 Experiments: Re=ΩR/ν=1.23×10 6 KT 10KQ KTD P J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 Experiments: Re=ΩR/ν=1.23×10 6 Rigid Wake Model KT 10KQ KTD P J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 Experiments: Re=ΩR/ν=1.23×10 6 Rigid Wake Model Wake Alignment Model (WAM) KT 10KQ KTD P smp’17 Espoo, Finland June 12-15 5
  • 22.
    Open-Water Prediction Ka4-70 (P/D=1.0)inside Duct 19Am (shart duct t.e.) J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 Experiments: Re=ΩR/ν=1.23×10 6 KT 10KQ KTD P J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 Experiments: Re=ΩR/ν=1.23×10 6 Rigid Wake Model KT 10KQ KTD P J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 Experiments: Re=ΩR/ν=1.23×10 6 Rigid Wake Model Wake Alignment Model (WAM) KT 10KQ KTD P J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 Experiments: Re=ΩR/ν=1.23×10 6 Rigid Wake Model Wake Alignment Model (WAM) WAM with Duct Boundary Layer Correction KT 10KQ KTD P smp’17 Espoo, Finland June 12-15 5
  • 23.
    New Wake Model Loadingis critically dependent on the blade wake pitch, especially at tip RANS Panel Method smp’17 Espoo, Finland June 12-15 6
  • 24.
    New Kutta Condition Locationof the pressure-equality points as percentage of the duct length 0.40 0.45 0.50 0.55 0.60 Duct 19A 100.0% 99.9% 99.8% 99.5% 99.0% 97.0% 96.5% 98.0% smp’17 Espoo, Finland June 12-15 7
  • 25.
    Open-Water Prediction Ka4-70 (P/D=1.0)inside Duct 19A J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 Experiments WAM, Closed Gap, Location at 97%, δ/R=4% WAM, Closed Gap, Location at 98%, δ/R=4% WAM, Closed Gap, Location at 99%, δ/R=4% KT 10KQ KT D P smp’17 Espoo, Finland June 12-15 8
  • 26.
  • 27.
  • 28.
    Motivation Panel Method: Gap model(closed) smp’17 Espoo, Finland June 12-15 9
  • 29.
    Motivation Panel Method: Gap model(closed) Wake alignment model smp’17 Espoo, Finland June 12-15 9
  • 30.
    Motivation Panel Method: Gap model(closed) Wake alignment model Correction due to duct boundary layer smp’17 Espoo, Finland June 12-15 9
  • 31.
    Motivation Panel Method: Gap model(closed) Wake alignment model Correction due to duct boundary layer New Kutta condition for thick duct t.e. smp’17 Espoo, Finland June 12-15 9
  • 32.
    Motivation Panel Method: Gap model(closed) Wake alignment model Correction due to duct boundary layer New Kutta condition for thick duct t.e. Significant differences in the performance prediction close to bollard pull condition! smp’17 Espoo, Finland June 12-15 9
  • 33.
    Motivation Panel Method: Gap model(closed) Wake alignment model Correction due to duct boundary layer New Kutta condition for thick duct t.e. Significant differences in the performance prediction close to bollard pull condition! Comparison between Panel Method and RANS calculations smp’17 Espoo, Finland June 12-15 9
  • 34.
    Motivation Panel Method: Gap model(closed) Wake alignment model Correction due to duct boundary layer New Kutta condition for thick duct t.e. Significant differences in the performance prediction close to bollard pull condition! Comparison between Panel Method and RANS calculations smp’17 Espoo, Finland June 12-15 9
  • 35.
    Numerical Methods smp’17 Espoo,Finland June 12-15 10
  • 36.
    Numerical Methods Panel CodePROPAN smp’17 Espoo, Finland June 12-15 10
  • 37.
    Numerical Methods Panel CodePROPAN IST in-house low-order potential-based panel method smp’17 Espoo, Finland June 12-15 10
  • 38.
    Numerical Methods Panel CodePROPAN IST in-house low-order potential-based panel method Fredholm integral equation solved by the collocation method smp’17 Espoo, Finland June 12-15 10
  • 39.
    Numerical Methods Panel CodePROPAN IST in-house low-order potential-based panel method Fredholm integral equation solved by the collocation method Structured surface grids smp’17 Espoo, Finland June 12-15 10
  • 40.
    Numerical Methods Panel CodePROPAN IST in-house low-order potential-based panel method Fredholm integral equation solved by the collocation method Structured surface grids RANS Code ReFRESCO smp’17 Espoo, Finland June 12-15 10
  • 41.
    Numerical Methods Panel CodePROPAN IST in-house low-order potential-based panel method Fredholm integral equation solved by the collocation method Structured surface grids RANS Code ReFRESCO Viscous flow CFD code (development led by MARIN) smp’17 Espoo, Finland June 12-15 10
  • 42.
    Numerical Methods Panel CodePROPAN IST in-house low-order potential-based panel method Fredholm integral equation solved by the collocation method Structured surface grids RANS Code ReFRESCO Viscous flow CFD code (development led by MARIN) Finite volume discretisation smp’17 Espoo, Finland June 12-15 10
  • 43.
    Numerical Methods Panel CodePROPAN IST in-house low-order potential-based panel method Fredholm integral equation solved by the collocation method Structured surface grids RANS Code ReFRESCO Viscous flow CFD code (development led by MARIN) Finite volume discretisation Turbulence model: k − ω SST 2-equation model by Menter (1994) smp’17 Espoo, Finland June 12-15 10
  • 44.
    Numerical Methods Panel CodePROPAN IST in-house low-order potential-based panel method Fredholm integral equation solved by the collocation method Structured surface grids RANS Code ReFRESCO Viscous flow CFD code (development led by MARIN) Finite volume discretisation Turbulence model: k − ω SST 2-equation model by Menter (1994) No wal functions are used (y+ ∼ 1) smp’17 Espoo, Finland June 12-15 10
  • 45.
    Grids PROPAN (left) andReFRESCO (right) Blade: 50×26 27M Cells Duct: 190×160 smp’17 Espoo, Finland June 12-15 11
  • 46.
    Blade Pressure Distributionat J = 0.5 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.5 0.0 0.5 1.0 RWM r/R=0.95 Cp=-1.0 smp’17 Espoo, Finland June 12-15 12
  • 47.
    Blade Pressure Distributionat J = 0.5 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.5 0.0 0.5 1.0 RWM r/R=0.95 Cp=-1.0 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.5 0.0 0.5 1.0 RWM WAM r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -0.5 0.0 0.5 1.0 smp’17 Espoo, Finland June 12-15 12
  • 48.
    Blade Pressure Distributionat J = 0.5 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.5 0.0 0.5 1.0 RWM r/R=0.95 Cp=-1.0 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.5 0.0 0.5 1.0 RWM WAM r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -0.5 0.0 0.5 1.0 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.5 0.0 0.5 1.0 ReFRESCO RWM WAM r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -0.5 0.0 0.5 1.0 smp’17 Espoo, Finland June 12-15 12
  • 49.
    Duct Pressure Distributionat J = 0.5 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.2 -0.1 0.0 0.1 RWM θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 smp’17 Espoo, Finland June 12-15 13
  • 50.
    Duct Pressure Distributionat J = 0.5 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.2 -0.1 0.0 0.1 RWM θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.2 -0.1 0.0 0.1 RWM WAM θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 smp’17 Espoo, Finland June 12-15 13
  • 51.
    Duct Pressure Distributionat J = 0.5 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.2 -0.1 0.0 0.1 RWM θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.2 -0.1 0.0 0.1 RWM WAM θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.2 -0.1 0.0 0.1 ReFRESCO RWM WAM θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 smp’17 Espoo, Finland June 12-15 13
  • 52.
    Blade Pressure Distributionat J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM r/R=0.95 Cp =-4.0 smp’17 Espoo, Finland June 12-15 14
  • 53.
    Blade Pressure Distributionat J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM r/R=0.95 Cp =-4.0 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM WAM r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -2.0 -1.5 -1.0 -0.5 0.0 0.5 1.0 smp’17 Espoo, Finland June 12-15 14
  • 54.
    Blade Pressure Distributionat J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM r/R=0.95 Cp =-4.0 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM WAM r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -2.0 -1.5 -1.0 -0.5 0.0 0.5 1.0 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 ReFRESCO RWM WAM r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -2.0 -1.5 -1.0 -0.5 0.0 0.5 1.0 smp’17 Espoo, Finland June 12-15 14
  • 55.
    Duct Pressure Distributionat J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM θ=0º smp’17 Espoo, Finland June 12-15 15
  • 56.
    Duct Pressure Distributionat J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM θ=0º s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM WAM θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 smp’17 Espoo, Finland June 12-15 15
  • 57.
    Duct Pressure Distributionat J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM θ=0º s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM WAM θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 ReFRESCO RWM WAM θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 smp’17 Espoo, Finland June 12-15 15
  • 58.
    Reduced Gap Pitch(P/D=0.9) X Y Z Blade Blade Wake Gap Strip smp’17 Espoo, Finland June 12-15 16
  • 59.
    Reduced Gap Pitch(P/D=0.9) X Y Z Blade Blade Wake Gap Strip X Y Z Blade Blade Wake Gap Strip smp’17 Espoo, Finland June 12-15 16
  • 60.
    Tip Leakage Flow smp’17Espoo, Finland June 12-15 17
  • 61.
    Pressure Distribution atJ = 0.5 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.5 0.0 0.5 1.0 ReFRESCO RWM WAM WAM with Reduced Gap Pitch r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -0.5 0.0 0.5 1.0 smp’17 Espoo, Finland June 12-15 18
  • 62.
    Pressure Distribution atJ = 0.5 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.2 -0.1 0.0 0.1 ReFRESCO RWM WAM WAM with Reduced Gap Pitch θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 smp’17 Espoo, Finland June 12-15 19
  • 63.
    Blade Pressure Distributionat J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM r/R=0.95 Cp =-4.0 smp’17 Espoo, Finland June 12-15 20
  • 64.
    Blade Pressure Distributionat J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM r/R=0.95 Cp =-4.0 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM WAM r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -2.0 -1.5 -1.0 -0.5 0.0 0.5 1.0 smp’17 Espoo, Finland June 12-15 20
  • 65.
    Blade Pressure Distributionat J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM r/R=0.95 Cp =-4.0 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM WAM r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -2.0 -1.5 -1.0 -0.5 0.0 0.5 1.0 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM WAM WAM with Reduced Gap Pitch r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -2.0 -1.5 -1.0 -0.5 0.0 0.5 1.0 smp’17 Espoo, Finland June 12-15 20
  • 66.
    Blade Pressure Distributionat J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM r/R=0.95 Cp =-4.0 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM WAM r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -2.0 -1.5 -1.0 -0.5 0.0 0.5 1.0 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 RWM WAM WAM with Reduced Gap Pitch r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -2.0 -1.5 -1.0 -0.5 0.0 0.5 1.0 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 ReFRESCO RWM WAM WAM with Reduced Gap Pitch r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -2.0 -1.5 -1.0 -0.5 0.0 0.5 1.0 smp’17 Espoo, Finland June 12-15 20
  • 67.
    Duct Pressure Distributionat J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM θ=0º smp’17 Espoo, Finland June 12-15 21
  • 68.
    Duct Pressure Distributionat J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM θ=0º s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM WAM θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 smp’17 Espoo, Finland June 12-15 21
  • 69.
    Duct Pressure Distributionat J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM θ=0º s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM WAM θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM WAM WAM with Reduced Gap Pitch θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 smp’17 Espoo, Finland June 12-15 21
  • 70.
    Duct Pressure Distributionat J = 0.1 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM θ=0º s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM WAM θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 RWM WAM WAM with Reduced Gap Pitch θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 ReFRESCO RWM WAM WAM with Reduced Gap Pitch θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 smp’17 Espoo, Finland June 12-15 21
  • 71.
    Open-Water Prediction Ka4-70 (P/D=1.0)inside Duct 19A J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 Experiments KT 10KQ KT D P smp’17 Espoo, Finland June 12-15 22
  • 72.
    Open-Water Prediction Ka4-70 (P/D=1.0)inside Duct 19A J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 Experiments KT 10KQ KT D P J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 Experiments ReFRESCO KT 10KQ KT D P smp’17 Espoo, Finland June 12-15 22
  • 73.
    Open-Water Prediction Ka4-70 (P/D=1.0)inside Duct 19A J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 Experiments KT 10KQ KT D P J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 Experiments ReFRESCO KT 10KQ KT D P J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 Experiments ReFRESCO WAM KT 10KQ KT D P smp’17 Espoo, Finland June 12-15 22
  • 74.
    Open-Water Prediction Ka4-70 (P/D=1.0)inside Duct 19A J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 Experiments KT 10KQ KT D P J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 Experiments ReFRESCO KT 10KQ KT D P J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 Experiments ReFRESCO WAM KT 10KQ KT D P J 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 Experiments ReFRESCO WAM WAM with Reduced Gap Pitch KT 10KQ KT D P smp’17 Espoo, Finland June 12-15 22
  • 75.
  • 76.
    Conclusions Prediction of theducted propeller loading is critically dependent on the blade wake pitch, especially at tip! smp’17 Espoo, Finland June 12-15 23
  • 77.
    Conclusions Prediction of theducted propeller loading is critically dependent on the blade wake pitch, especially at tip! The flow in the tip region is particularly important near bollard pull smp’17 Espoo, Finland June 12-15 23
  • 78.
    Conclusions Prediction of theducted propeller loading is critically dependent on the blade wake pitch, especially at tip! The flow in the tip region is particularly important near bollard pull Future work: smp’17 Espoo, Finland June 12-15 23
  • 79.
    Conclusions Prediction of theducted propeller loading is critically dependent on the blade wake pitch, especially at tip! The flow in the tip region is particularly important near bollard pull Future work: Include reduction of the gap strip in wake alignment model smp’17 Espoo, Finland June 12-15 23
  • 80.
    Conclusions Prediction of theducted propeller loading is critically dependent on the blade wake pitch, especially at tip! The flow in the tip region is particularly important near bollard pull Future work: Include reduction of the gap strip in wake alignment model Robustness issues are expected smp’17 Espoo, Finland June 12-15 23
  • 81.
    Pressure Distribution atJ = 0.2 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.5 0.0 0.5 ReFRESCO RWM WAM WAM with Reduced Gap Pitch r/R=0.95 s/c Cp 0.00 0.01 0.02 0.03 0.04 0.05 -2.0 -1.5 -1.0 -0.5 0.0 0.5 1.0 s/c Cp 0.0 0.2 0.4 0.6 0.8 1.0 -0.3 -0.2 -0.1 0.0 0.1 ReFRESCO RWM WAM WAM with Reduced Gap Pitch θ=0º s/c Cp 0.80 0.85 0.90 0.95 1.00 -0.03 -0.02 -0.01 0.00 0.01 0.02 smp’17 Espoo, Finland June 12-15 24
  • 82.
    Wake Geometry atJ = 0.2 x/R = 0.2 x/R = 0.4 smp’17 Espoo, Finland June 12-15 25
  • 83.
    Wake Geometry atJ = 0.2 smp’17 Espoo, Finland June 12-15 26
  • 84.
    Wake Geometry atJ = 0.1 x/R = 0.2 x/R = 0.4 smp’17 Espoo, Finland June 12-15 27
  • 85.
    Wake Geometry atJ = 0.1 smp’17 Espoo, Finland June 12-15 28
  • 86.
    Wake Geometry atJ = 0.5 x/R = 0.2 x/R = 0.4 smp’17 Espoo, Finland June 12-15 29
  • 87.
    Influence of theWake Model Model KTP KTD 10KQ J = 0.1 RWM 0.412 0.206 0.5882 WAM 0.313 0.231 0.4664 WAM with Reduced Gap Pitch 0.284 0.226 0.4228 Experiments 0.254 0.214 0.4387 J = 0.2 RWM 0.383 0.160 0.5538 WAM 0.297 0.176 0.4456 WAM with Reduced Gap Pitch 0.273 0.171 0.4083 Experiments 0.248 0.166 0.4279 J = 0.5 RWM 0.266 0.054 0.4041 WAM 0.208 0.057 0.3246 WAM with Reduced Gap Pitch 0.193 0.055 0.3010 Experiments 0.196 0.053 0.3506 smp’17 Espoo, Finland June 12-15 30
  • 88.
    Wake Model Rigid wake X Y Z smp’17Espoo, Finland June 12-15 31
  • 89.
    Wake Model Aligned wakewith b.l. correction X Y Z smp’17 Espoo, Finland June 12-15 32