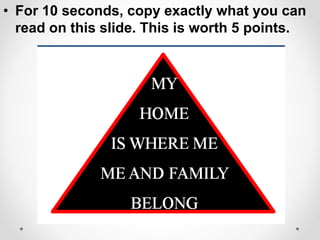
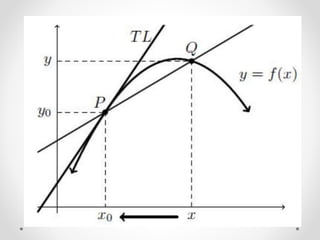
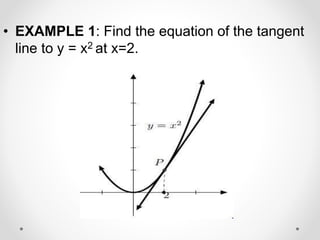
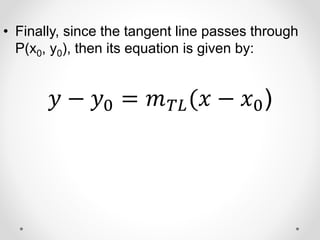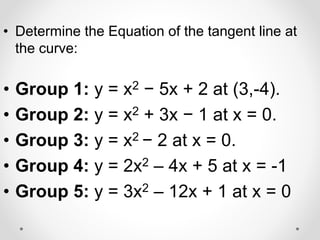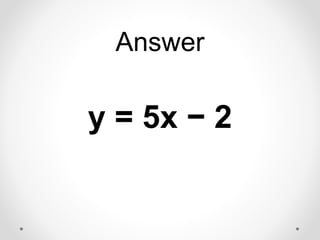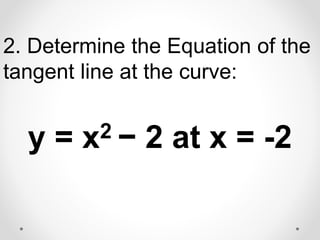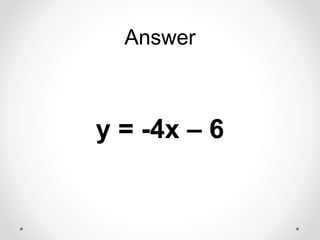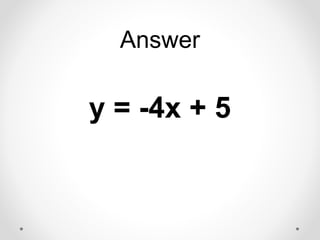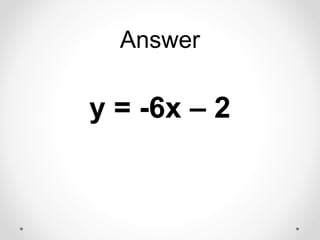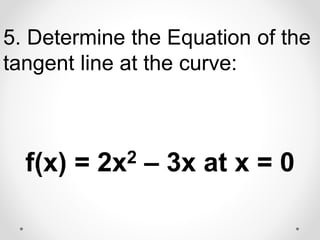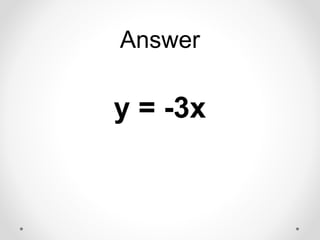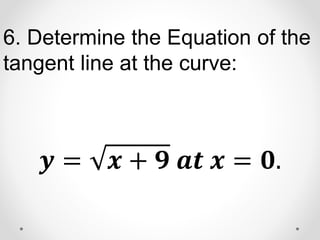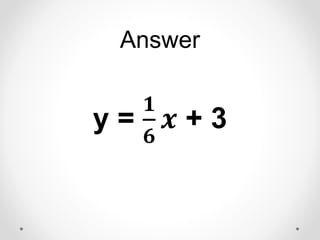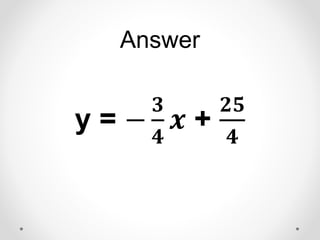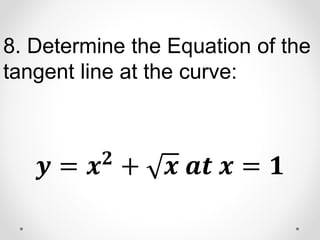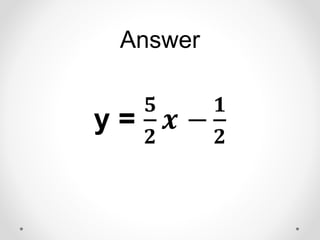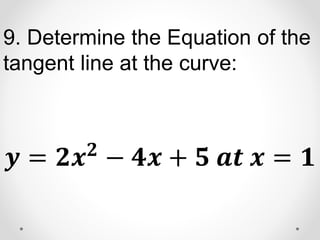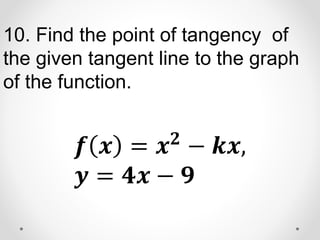The document provides instructions and examples for finding the equations of tangent lines to various functions. It includes exercises for students to calculate tangent lines at specified points, alongside a team quiz with solutions for verification. The core concept discussed is the derivation of the slope of the tangent line as a limit of secant lines approaching a given point on the graph.